用于毒理学分析的实用沉降仿真 App

沉降是一种简单的物理现象，颗粒或团块由于重力或离心力在溶液中沉降。由于这种现象非常简单，因此广泛应用于毒理学、生物化学、生物医学、遗传学和制药工程等许多技术领域。在这篇博客中，我们将讨论一个关于重力如何影响试管中的沉降的数学模型，以及如何制作一个用于纳米毒理学的实用仿真 App (作为各种应用中的一个示例)。

提取的 DNA，其中的颗粒沉淀到试管底部。图片由 Isaevde 提供。通过Wikimedia Commons获得许可(CC BY-SA 4.0)。

沉降如何应用在生物化学领域

自 2020 年 3 月以来，COVID-19 大流行的传播以不同的方式影响着我们的生活。你可能在旅行或工作之前已经做过聚合酶链反应 (PCR) 测试，这是测试 COVID-19 最常用的技术之一。众所周知，Kary Mullis 和 Michael Smith是 PCR 的发明者，并因此获得 1993 年诺贝尔奖。同样，COVID- 19 的大流行也需要 COVID-19 疫苗，希望它能够防止病毒传播。基于 mRNA 的 SARS-CoV-2 疫苗背后技术的主要贡献者Drs.Drew Weissman 和 Katalin Karikó被授予了 2021 年拉斯克奖，这是美国最高的生物医学研究奖。

在 COVID-19 大流行期间，我们几乎每天都会不自觉地听到和看到许多基因工程术语，例如病毒、疫苗、PCR和mRNA等。这些术语都由生物分子组成，或与其相关。各种各样的生物分子都可以通过离心机的沉降系数来表征。这项研究的先驱是瑞典化学家Theodor Svedberg，他因对分散系统的研究而获得 1926 年的诺贝尔奖。他的姓的首字母现在是沉降系数的单位名称（S，svedberg），表示粒子在一定力（重力或离心力）的作用下达到终速的速度。例如，完整的真核生物核糖体的沉降系数为 80 S。

虽然COVID-19 被认为是一种自然疾病，但也存在人为疾病，例如，由工厂、汽车和其他人为排放的材料和污染源引起的各种尺寸（从纳米到微米）的颗粒（通常是金属）造成的空气污染。毒理学领域研究这些颗粒如何对人类健康造成损害。剂量学是解决体内（动物测试）和体外（基于细胞的测定）结果之间差异的关键技术之一。对颗粒剂量和浓度的更加准确的量化和预测，将有助于体外实验更加准确。为此，使用了沉降实验和模拟。

在生物医学研究中，血液沉降被用于研究人体炎症。更快的沉降意味着更多的炎症，也是某些以产生异常蛋白质为特征的疾病的迹象，例如多发性骨髓瘤。沉淀也被用于分离白细胞、红细胞和血小板。在制药应用中，沉降法被用于从结晶后的母液中分离药物，以及从其他蛋白质材料中提纯胰岛素（“制药工业中的离心法综述”）。药物吸附和解吸的研究对制药工业也很重要。

大量非常重要的应用都使用沉降。虽然沉降或离心可以相对容易和快速地进行实验，但是使用计算机绝对更有利，因为可以一次模拟材料和条件的多种组合。此外，数学建模对于理解复杂的沉降现象（如吸附和解吸）通常是必不可少的。

重力作用下的试管沉降方程

在生物工程、基因工程、医学工程和制药应用中，超高速离心机被用于分离颗粒或分子。这主要是因为生物大分子比其他类型的颗粒“更黏”，往往需要更大的力才能沉降。想象一下含有 DNA/RNA 的生物材料有多黏：地球和太阳之间距离的 90 倍被缠绕在一起，装在一对 DNA 链里。有些商业离心机可以产生高达 70000 g （这里是指重力单位）的力。有些离心机上装有激光源，照射在水平旋转的试管上，可以实时测量浓度。

用于描述离心沉降的控制方程称为Lamm 方程。Ole Lamm 是 Svedberg 的博士生。这个方程只是Mason-Weaver 方程在柱坐标下的形式，接下我们将对它进行讨论。

与生物分子相比，用于毒理学研究的颗粒（通常是金属或陶瓷）更重、下沉更快。因此，在这些应用中，重力完成了这一工作。将试管垂直放置，颗粒会垂直下沉，如下图所示。

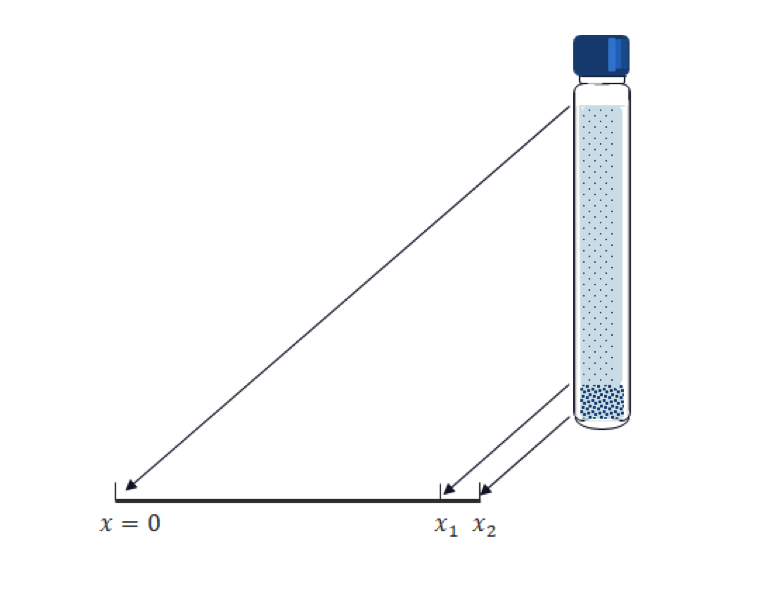
将垂直位置转换为一维坐标x；对于给定的管长度x_2和计算时间T，可以得到以下 Mason-Weaver 方程：

其中，c是粒子浓度，待求解的变量A和B分别为粒子的扩散系数和沉降速度；g是重力加速度。

管顶部和底部的边界条件就是所谓的零通量边界条件，即

这个条件意味着边界上的总质量通量(不仅是扩散通量)为零；也就是说，下沉的颗粒在底部积累，因为它们无法排出试管。我们的主要兴趣是粒子的累积质量。为了测量，我们需要设置一个虚构的体积(一维中的段)。在上述几何图形中，区间[x_1. x_2]就是为此而准备的。请注意，计算出的累积质量因区间大小而异。

初始条件通常均匀分布，如下所示：

式中，c_0是一个常数函数。

现在，我们有了模拟沉降的所有公式。

Mason-Weaver 方程是一个容易理解和求解的方程，除了极快的沉降情况。让我们试着解释一下它的物理意义。它由两个方程组成：

1. 扩散（第二项）
2. 重力对流（第三项）

如果我们分别考虑每个现象，会发现对这个方程的解释其实很容易。首先，重的颗粒迅速下沉，几乎没有扩散，并积聚在试管底部。最初，颗粒是均匀分布的。随着沉降的开始，颗粒从顶部消失，底部周围的颗粒数量增加。最后，几乎所有的颗粒都聚集在底部，这意味着浓度函数变得像试管底部的δ函数。较轻的颗粒倾向于漂浮在溶液中，因为它们不受重力影响。这两种现象在现实中是同时发生的。我们用下面的动画演示了两个极端情况。

较重的颗粒(左)和较轻的颗粒(右)的空间浓度分布比较。

粒度分布颗粒沉降仿真 App

上图所示的情况比较简单。然而，在现实世界中，颗粒通常不会单独漂浮在溶液中，并且通常会根据表面电荷或颗粒可能具有的某些结合机制，形成不同尺寸的团聚体。在溶液中，不同大小的团聚体表现不同，正如我们在上面的动画中看到的那样。因此，想象整体浓度分布的样子便不再那么容易了。在 COMSOL Multiphysics^®软件用户界面使用偏微分方程可以很轻松地模拟单个粒径的 Mason-Weaver 方程，但要模拟更实际的情况并不容易，因为必须考虑粒度分布或其他一些条件或约束。在这种情况下，制作仿真 App 可以提供更大的灵活性和更令人满意的结果。

在下面的部分，我们将演示一些（但不是全部）关键步骤，来制作一个重现 DeLoid 引用的论文结果的仿真 App。

步骤1

在模型开发器中设置几何、材料、基本物理场以及初始条件和边界条件。

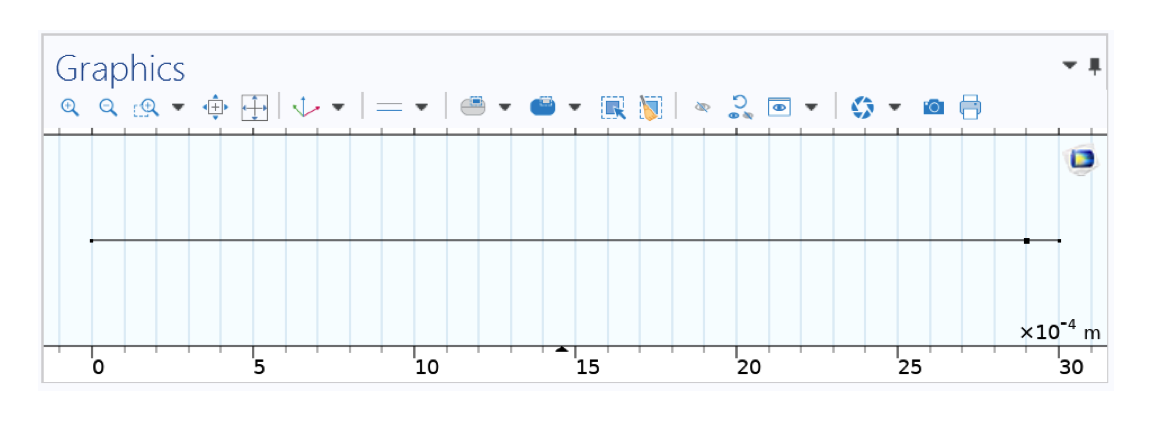
代表试管的一维几何图形(左侧为盖子，右侧为底部)。

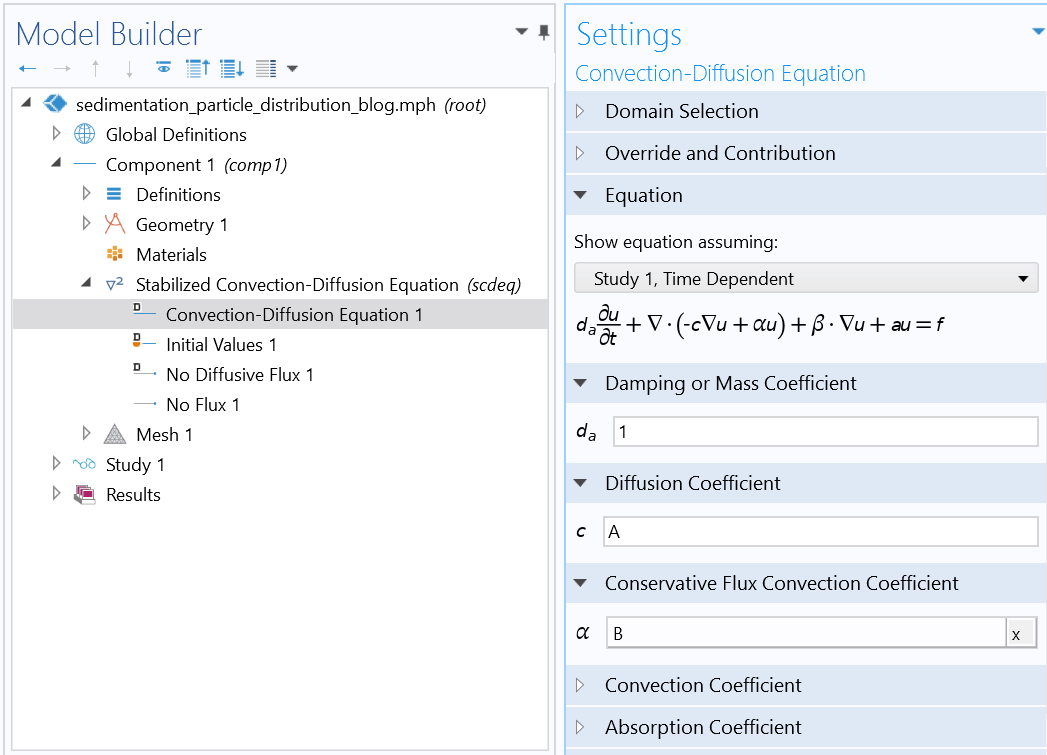
使用经典偏微分方程接口中的稳定对流-扩散方程接口设置 Mason-Weaver 方程。

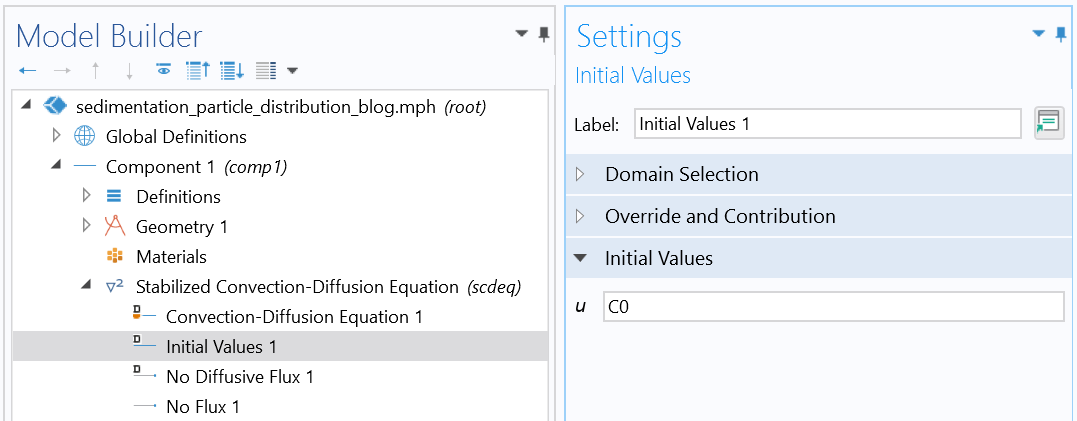
初始条件(均匀分布)。

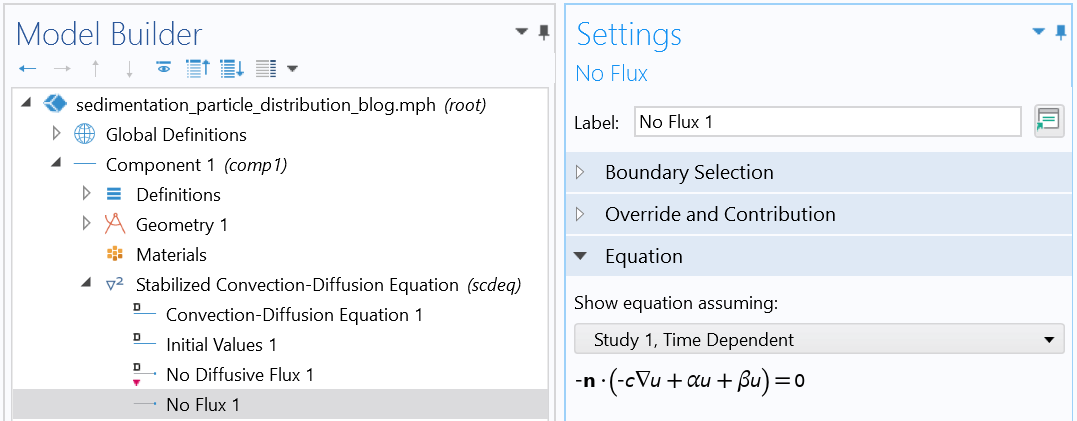
边界条件(反射边界条件)。

步骤2

在 App 开发器中制作自定义 App 的用户界面。

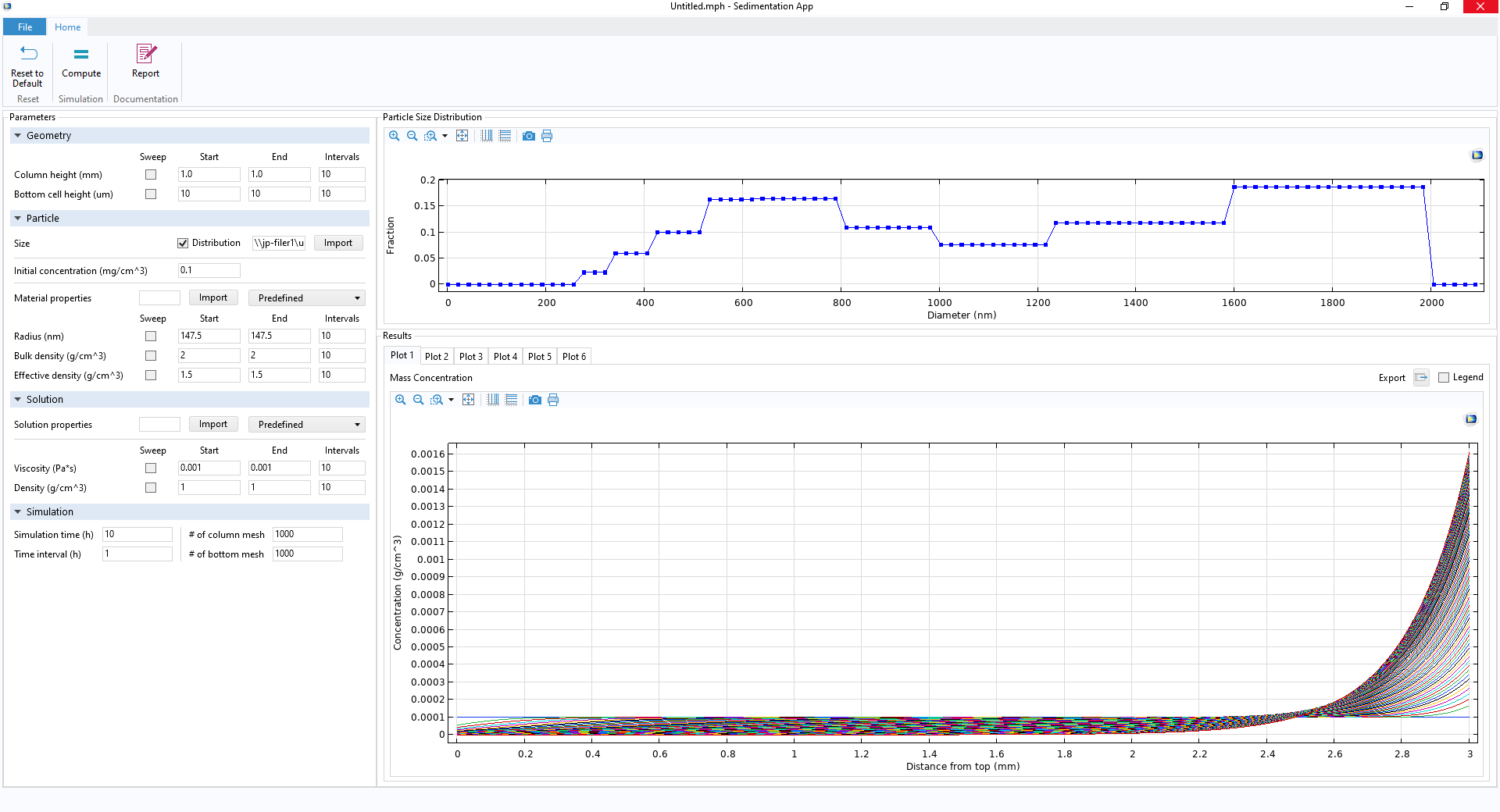
自定义仿真 App 的用户界面，包括几个功能区按钮(顶部)、参数设置窗口(左)、粒度分布曲线(右上)和结果图形窗口(右下)。

步骤3

编写 Java^®代码。

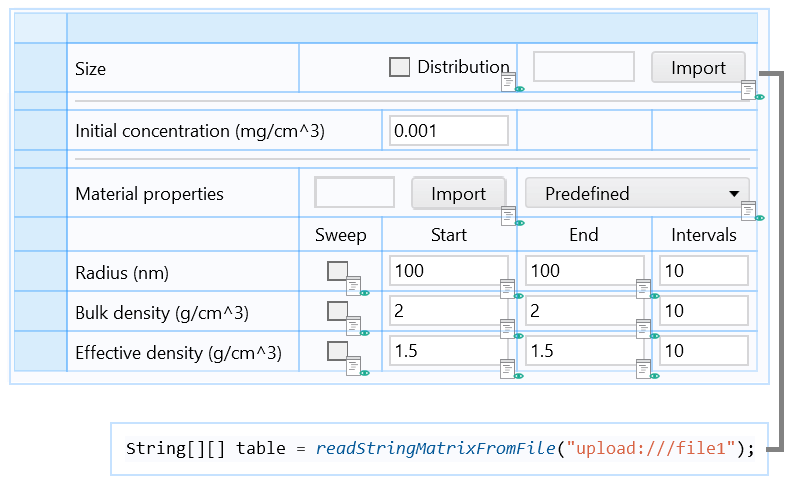
表单的一部分包括与 Java 方法关联的导入按钮，该方法从文件加载粒度分布数据并将其存储在二维字符串数组中。

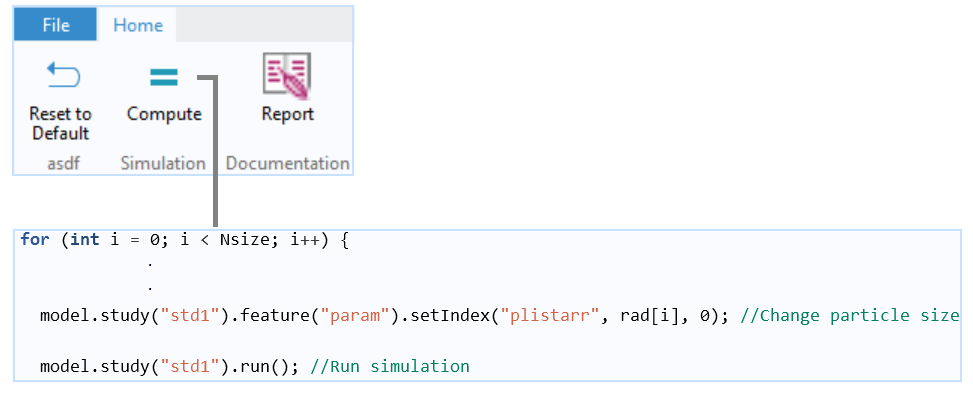
一个用于主 for-end 循环的 Java 方法，对每个更新的粒子大小重复运行。底部的粒子质量是在每个时间步长下被计算出来的，并存储在二维双精度浮点数组（未显示）中。在运行结束时，将粒子质量相加来计算在底部累积的总质量分数。

使用按照上述步骤制作的这个仿真 App，我们可以获得如下图所示的最终结果。本例中使用的颗粒是 CeO₂，它相对较重，容易在底部快速下沉和堆积，如下图（蓝线）所示。颗粒大小显著影响质量分数。较小的颗粒倾向于通过扩散漂浮，而不会一直下沉。因此，当考虑大小分布时，质量分数达到稳定的速度更慢，低于 100%。

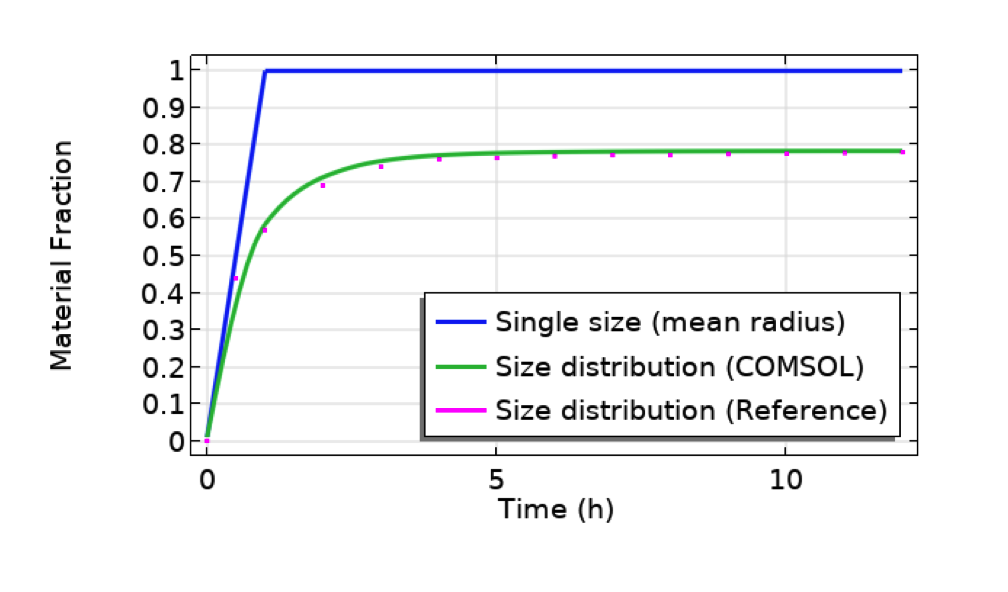
单个粒径(上图用户界面中显示的分布曲线的平均半径为 491nm)和粒径分布的比较(COMSOL Multiphysics 与参考论文的结果一致性较好)。颗粒：CeO₂。试管长度：10mm。底部长度：10um。

附加说明

系数A和B可以通过实验得出，或者通过下面列出的流体动力学关系从材料属性中计算。

式中，k_B, \ T, \ \eta, \ r分别是玻尔兹曼常数、温度、溶液的动态黏度和粒子的半径，\rho_e和\rho_s分别是粒子的有效密度和溶液的密度。

如果你想要增强这个仿真 App，可能需要修改或添加更多功能。对于制药或生物医学应用，可能需要考虑颗粒的可溶解性。在底部边界，可能需要考虑另一个解释吸附和解吸的边界条件，而不是反射边界条件。这些增量可以通过添加一个辅助方程来完成。详请参阅 Christmann、Ramteke 和 Dokoumetzidis 的文献。

下一步

单击下面的按钮，探索本文中讨论的沉降仿真 App。以此为灵感，尝试构建您自己的仿真 App，并在评论中告诉我们您的体验！

参考文献

1. G.M. DeLoid et al., “Advanced computational modeling for in vitro nanomaterial dosimetry”,Particle and fibre toxicology, vol. 12, no. 1, pp. 1–20, 2015.
2. K. Christmann,Introduction to Surface Physical Chemistry, Springer Science & Business Media, vol. 1., 2013.
3. K.H. Ramteke et al., “Mathematical models of drug dissolution: a review”,Sch. Acad. J. Pharm, vol. 3, no. 5, pp. 388–396, 2014.
4. A. Dokoumetzidis and P. Macheras, “A century of dissolution research: from Noyes and Whitney to the biopharmaceutics classification system”,International Journal of Pharmaceutics321.1-2 (2006): 1–11.

Oracle and Java are registered trademarks of Oracle and/or its affiliates.