
在许多仿真任务中,需要将变量从计算域的一个区域(源)转移到另一个域或组件(目标)。在 COMSOL Multiphysics 中,这种功能是通过定义一个点对点映射(即 拉伸算子),将一组目标点与一组源点相关联来实现的。一旦拉伸算子建立了映射,就可以使用相同的算子从目标访问在源处定义的所有变量。
在域之间映射变量
在许多实际情况中,需要将变量从一个组件或组件的一部分映射到另一个部分。两个子模型的连接就是这样一个实例,例如为湍流模型生成入口边界条件。入口处的边界条件明显影响域内的流体流动。然而,入口处的流动轮廓不像层流那样容易定义。为了产生湍流入口边界条件,可以使用法向流入的辅助模型。然后,需要将出口处的最终速度分布复制到主模型的入口。
效率可能是在域之间映射变量的另一个原因。例如,具有轴对称热边界条件和材料特性的热膨胀。如果结构边界条件不是轴对称的,我们可以通过先执行轴对称热分析,然后将温度从 2D 轴对称域映射到 3D 域进行结构分析以节省时间。
另一种常见的情况是周期性或其他边界条件的实现,其中边界上某个点的量与另一边界上某个点的量相关。例如,在二极管中,p-n 结一端的法向电流密度取决于同一点的电势和结另一端的电势。虽然在 COMSOL Multiphysics 的适当的物理接口中内置了大量这样的边界条件,但是用户有时可能会需要构建自己的边界条件。
以上这些情况都需要将变量从一个域或边界逐点映射到另一个域或边界。今天,我们为您展示将如何构建这些映射。
源和目标之间的映射
映射的思想涉及两个几何实体: 已知变量的源和将使用这些变量的目标。已知在源处的一个量,我们想计算目标域的另一个量。新的量可以与相同,或者是它的一个函数。
我们可以把这个问题分成以下几个步骤:
- 对于点 x_d,想要评估 q_d。
- 识别对应于点 x_d 的源点 x_s,此坐标变换由下式给出:x_s = T(x_d)。
- 提取 q_s = q_s(x_s)。
- 建立关于变量 q_s 的函数:f:q_s\rightarrow q_d 来计算 q_d。
然后得到
所以,本文的重点是转换 T : x_d \rightarrow x_s。
COMSOL Multiphysics 提供了两种耦合算子来指定这种映射: 线性拉伸算子 和广义拉伸算子。线性拉伸算子更容易构建,但它们的用途仅限于仿射变换。广义拉伸算子更通用,但需要更多的精力进行定义。
这里,我们将讨论线性拉伸算子。在下一篇博文中,我们将讨论广义拉伸算子。
在 COMSOL Multiphysics 中使用线性拉伸算子
当源点和目标点通过仿射变换(如平移、缩放、反射、旋转或剪切)相互关联时,COMSOL Multiphysics 提供了一种指定拉伸算子的简单方法:线性拉伸算子。要添加线性拉伸算子,我们可以选择:定义 > 非局部耦合 > 线性拉伸。
线性拉伸算子的基本思想是:如果我们知道线上的两对对应点时,就可以定义两条线之间的仿射变换。类似地,三对非共线点和四对非平面(不超过两个共线)点分别描述2D域和 3D 域的仿射映射。
这和一般的线性系统分析类似。如果我们知道足够数量的基点(或向量)的变换,就可以使用线性叠加来变换每个点(或向量)。将线性拉伸算子视为选择基础及其变换的可视化方式。根据这些信息,COMSOL Multiphysics 自动导出需要应用于任意点(或向量)的映射。
下面,我们将用几个例子来说明这一点。
示例1
第一个算子用于将数据从含有端点1和4的线段映射到含有端点4和5的线段,并保留方向。我们所需要做的就是向 COMSOL Multiphysics 指出哪个点通向哪里,如下图所示。
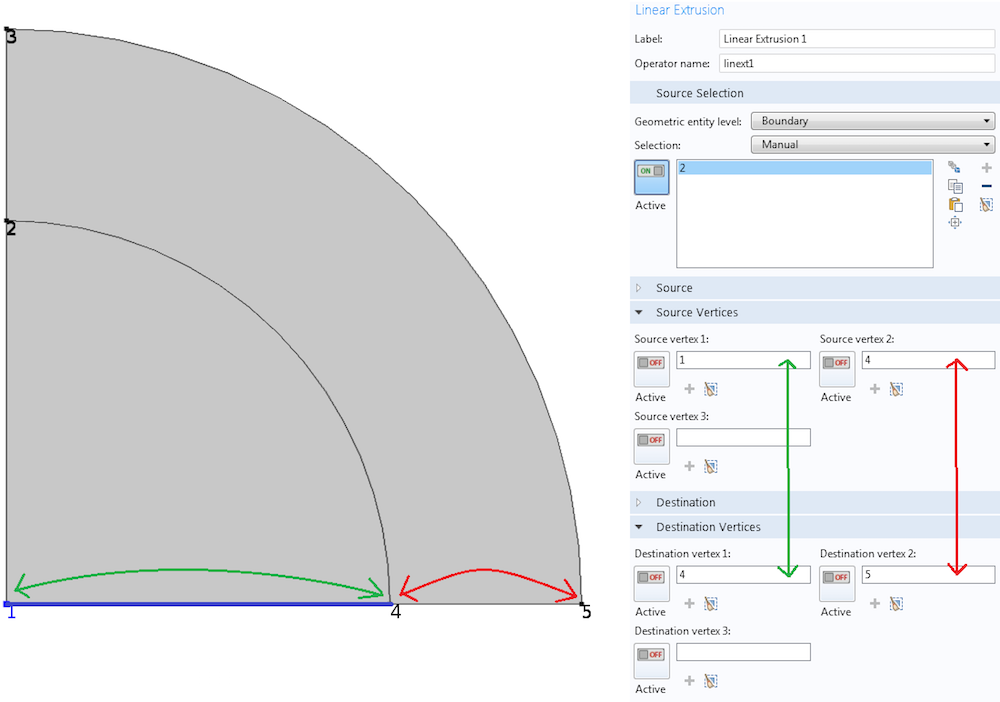
线性拉伸算子将源中的点1 和点4 分别匹配到目标的点4和5。
注意,即使我们在 2D 空间,也在处理 1D 对象(线)。因此,这足以表明两组顶点之间的对应关系。如果我们选择5 对应于目标顶点1,4对应于目标顶点2呢?在这种情况下,在线段 1-4 转换为线段 4-5 所需的平移和拉伸之外,还会有翻转。见下图。
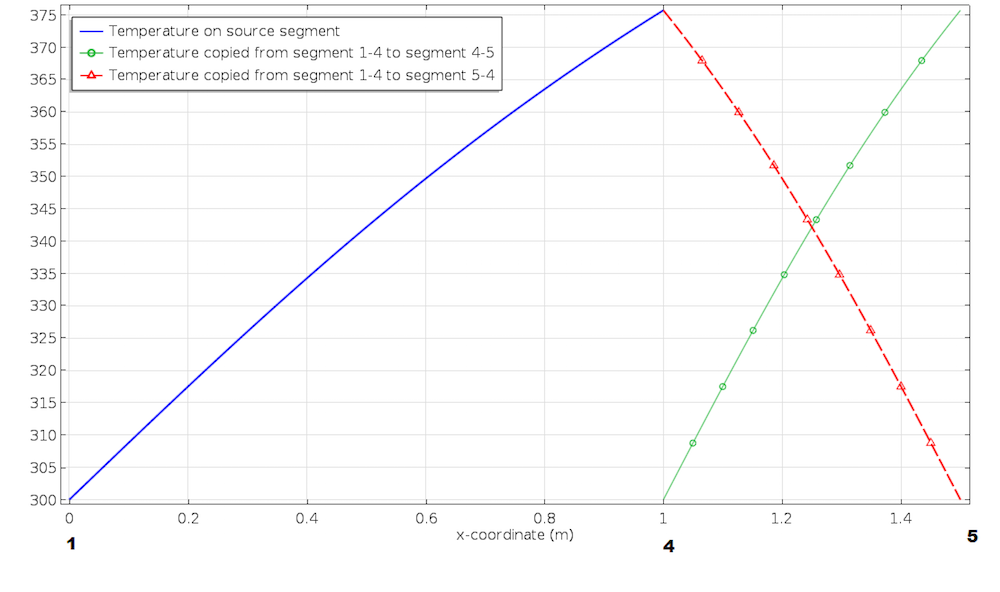
线性拉伸算子的“源顶点”和“目标顶点”下的顶点顺序决定了映射的方向。
示例2
现在,我们增加对象的维度,并建立线性拉伸算子,通过径向拉伸将数据从内部圆复制到外部域。我们需要做的就是在上面的顶点对上再增加一对顶点。参见下面的“线性拉伸设置”窗口。
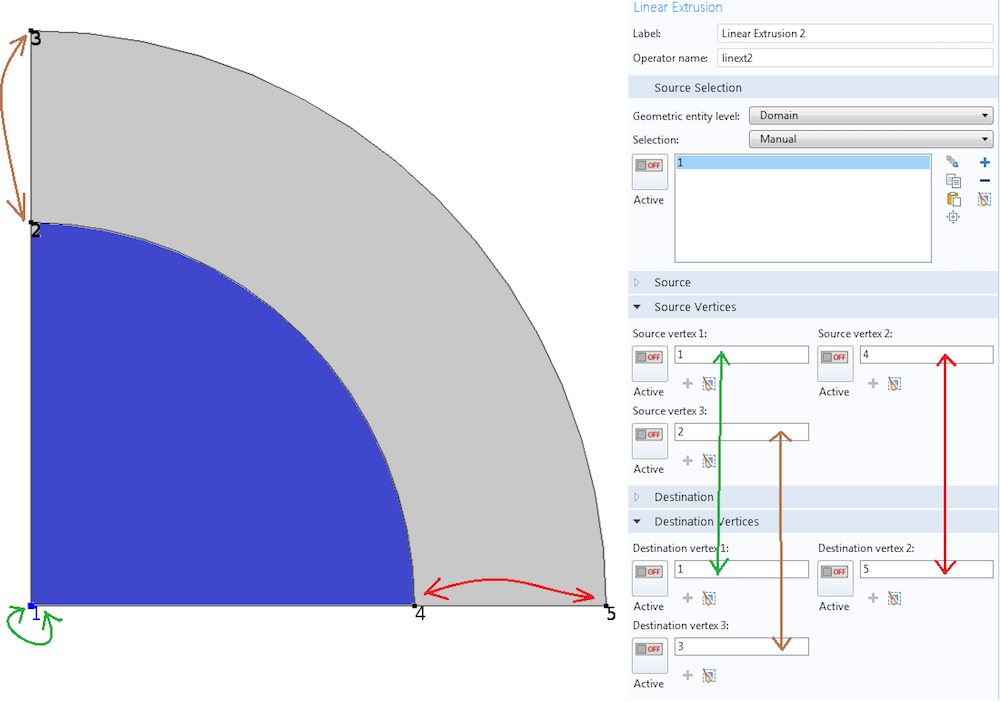
映射中对象的维度越大,几何图形中需要配对来定义线性拉伸算子的顶点就越多。
该映射将源域中的点 1、4 和 2 分别匹配到目标域中的点 1、5 和 3。如果我们从基本向量的角度来看,源中的线段1-4 对应于目标中的线段1-5。同样,源中的线段 1-2 对应于目标中的线段1-3。从这两个线性独立的基础上,COMSOL Multiphysics获得了足够的信息来构建从 2D 域中的任何目标点到源点的映射。下图显示了一个内部圆上定义的变量如何通过刚定义的线性拉伸算子 linext2 映射的。
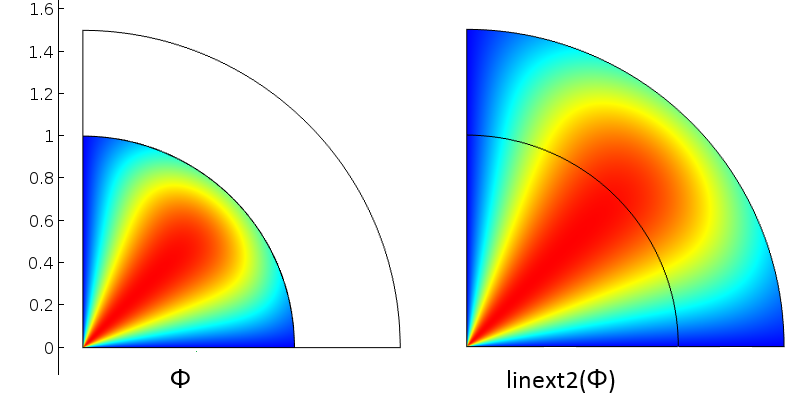
在内部圆上定义的变量(左),并使用线性拉伸算子映射到所有点(右)。
评估数量
到目前为止,我们所做的是建立基础结构,以帮助我们访问变量。现在,让我们看看如何使用我们构建的工具。
如果我们查看上面图像中显示的任何线性拉伸设置窗口,就会在顶部看到算子名称。我们将使用该名称来访问映射。如果 linext2 是拉伸算子名称,任何时候我们在目的点想要从相应的源点引用一个量,比如说 u,我们使用表达式 linext2(u)。如果想要从同一个源点获取变量 w,我们使用 linext2(w)。这可以解释为什么我们称他们为算子。一旦我们构建了它们,就可以将它们用于任何合理的变量。
如果我们想要变量的函数,可以将函数放在算子内部,或者将函数应用于算子的输出,而不是只使用变量。比如,linext2(w^2) 相当于linext2(w)^2。linext2(w)+u 是否 返回与 linext2(w+u) 相同的值?一般不会。第一种情况,是将目标点处的 u 加到相应的源点处计算的 w。第二种情况,u 和 w 都在源点计算。下图使用示例 2 中的线性拉伸算子说明了这一点。
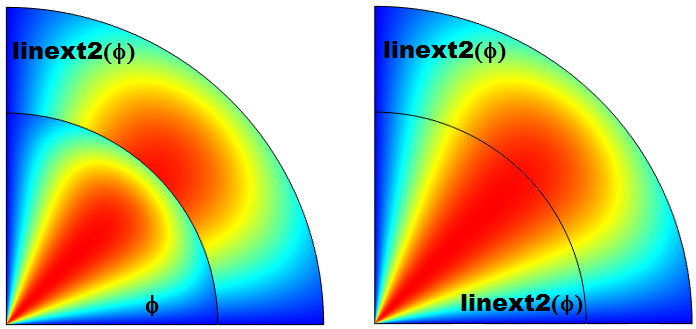
变量 \phi 内部圆部分是在目标点计算和外弧(左)部分是在源点计算。所有计算都在源进行(右)。请注意,一般来说,变量,例如 \phi,可以是目标处的有效量。在这种情况下,其值通常与拉伸算子返回的值不相同。
最后,当使用拉伸算子来映射不同组件之间的变量时,应将该算子添加到包含源对象的组件的定义 节点。当我们在另一个组件中使用该算子时,应该包含组件标记。使用线性拉伸算子 linext2 从组件2 访问组件1 定义的变量到,正确的语法是 comp1.linext2(comp1.u)。如果有一个拉伸或另一个算子,也称为 linext2,或者在第二个组件中有个变量也做 u ,这可以避免混淆。
结束语
这篇博文的重点是线性拉伸算子的构建。有关它们在完整建模问题中的使用,请参见后台阶湍流模拟的案例模型。在本例中,线性拉伸算子用于从湍流模拟的辅助分析中转换准确的入口速度。
敬请关注我们即将发布的关于如何构建广义拉伸算子的博文,我们将在一个完整的建模示例中说明它们的使用。同时,如果你有任何问题,请随时联系我们。



评论 (0)