
你有没有用手在墙上玩过皮影戏的游戏?从手(三维)后面照射一束光线,你就可以在墙上创建二维投影。使用 COMSOL 多物理场仿真软件分析仿真数据时,也可以使用投影算子对模型执行类似操作。
2D 轴对称管道流模型示例
假设你刚刚计算了 一个2D 轴对称管道流模型的解,其中包含由流动传输的化学物质 c。查看管道中浓度的空间分布,你会发现浓度在流动方向上降低。虽然可以在下面的表面图中清楚地看到这种流动趋势,但你可能还希望用定量的方式描述它。
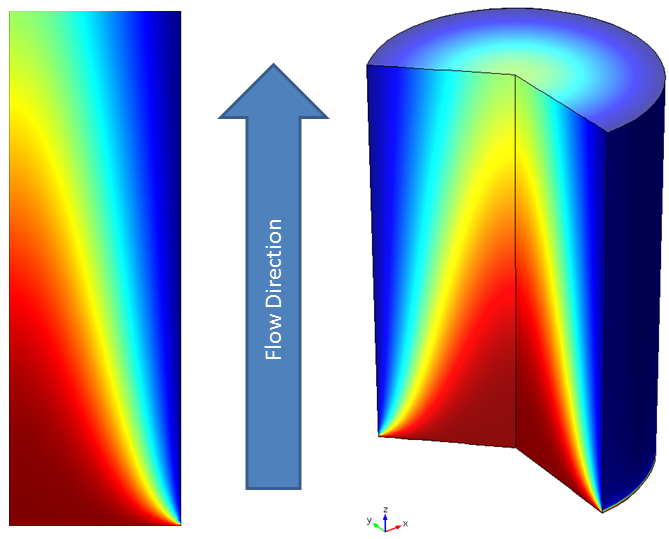
浓度和流向。
实现这个目标的一种方法是绘制沿管道轴线的每个横截面的平均浓度。在 COMSOL 中,你可以使用投影算子来执行此操作。
投影算子,将源维度减少 1
我们来回顾一下阴影成像类比,并思考一下它的概念是如何定义的。当你将手放在光源和墙壁之间时,手会阻挡光路,你可以看到墙壁上的阴影,即三维手的二维图像。
你可以将 COMSOL 软件中的投影算子看成制作模型“皮影戏”的工具。模型(或它的一部分)扮演手的角色。这在算子设置中称为源。 在这个类比中,墙相当于模型的另一部分:目标,是阴影形成的地方。
就像皮影戏一样,COMSOL 中的投影结果会将源的维度减少1。“图像”是通过在“光的方向”上整合一个表达式而形成的。这个方向由源和目标之间的映射指定。在软件中,你有两种选择:用于线性映射的线性投影和用于更复杂情况的广义投影。接下来,我们使用这些功能来绘制沿上面介绍的管道轴线的平均横截面浓度。
线性投影
假设你对沿流动管道轴线高度z的横截面上的平均物质浓度感兴趣。由于几何二维轴对称,因此横截面由水平线表示,并且可以使用以下积分计算平均值c_{av}(z):
式中,A(z)=\pi\cdot R(z)^2是横截面积,R(z)是积分的长度, 在本例中等于管道的半径。
在 COMSOL 软件中,这里显示的线积分可以使用线性投影算子求解。从上面的讨论中,可知需要一个源,目标和两者之间的映射来设置算子。将线性投影添加到组件的定义中时,首先选择属于源的几何实体。
在这个管道示例中,这是整个模型域 1。线性投影使用由所选顶点之间的线定义的线性映射。现在,已准备好设置映射,从目标开始。这里应该是流动管道的轴,因此可以相应地选择目标顶点 1 和 2。接下来,选择源中与目标对应的行。在这个方案中,这是同一条线,因此将相同的点分配给源顶点 1 和 2。源比目标多一个顶点,用于指定线积分的方向。在我们的示例中,此处选择顶点 3,意味着线积分的计算与该线平行,如下图中的白色箭头所示。
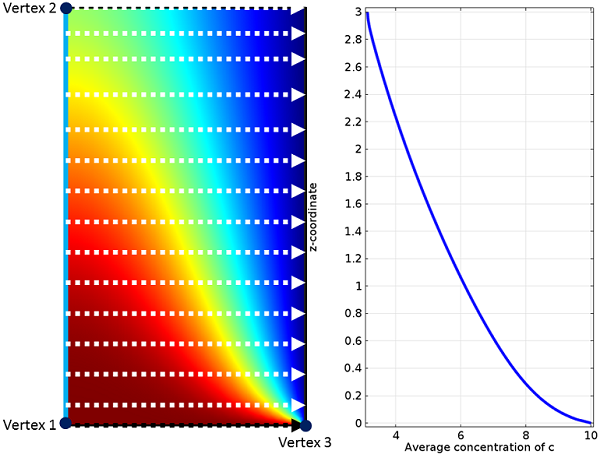
浓度箭头表示线积分和化学物质的平均浓度,c。
总而言之,第一个轴(顶点 1 和 2 之间)包含线积分的起点,而第二个轴(顶点 1 和 3 之间)给出积分的方向。
现在,你可以使用算子(默认称为“linproj1”)来积分 c 的浓度,并将其除以积分的长度来获得平均浓度。如果长度R(z)不是恒定的或未知的,那么算子也可以对其进行评估。下面是得到的等式:
如果要绘制结果,请使用一维折线图,使用 linproj1(c*2*pi*r)/linproj1(2*pi*r) 作为表达式,左边界作为选项。
广义投影
你还可以使用广义投影算子设置平均值。顾名思义,这个算子可以处理更复杂的映射,并且可以在其域的任何(弯曲)方向上使用路径积分。当然,你也可以使用广义投影算子来设置线性投影。当模型几何中没有顶点来充分设置线性投影算子时,该选项是相关的。在这种情况下,可以修改几何图形来包含必要的折点,也可以使用广义投影算子,在该算子中,可以直接使用数学表达式定义源和目标之间的映射。
为了更好地理解,让我们再看一下二维轴对称示例模型。将广义投影添加到组件的定义部分后,再次首先选择源几何图形。算子的设置包含一个用于定义源映射和目标映射的数学表达式字段。在本例中,表达式是坐标的线性函数。如果再次从目标开始,则在此几何图形中输入流动轴,即z轴。由于在源中使用了相同的行,因此那里的x表达式也是z轴。y表达式定义积分方向,在本例中为r轴。现在,可以使用广义投影算子(默认情况下称为“genproj1”)来获得与之前的线性投影相同的结果。
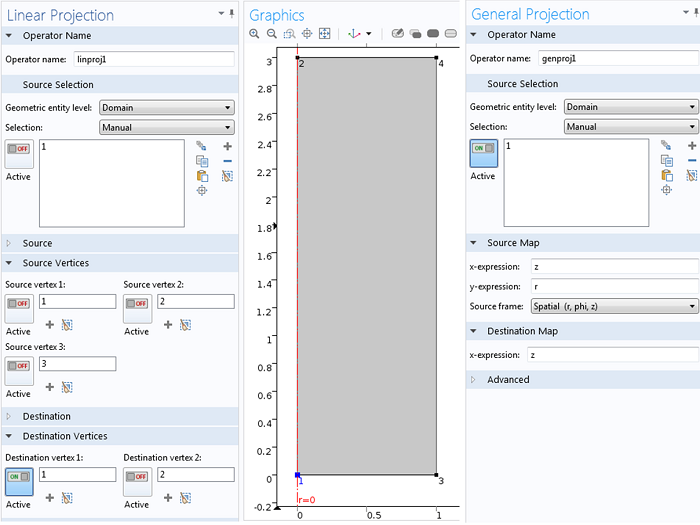
线性和广义投影算子的设置。
投影多个维度
如果你有一个三维模型,可能是由于浓度分布不对称产生的,该怎么办?在这种情况下,可以通过计算x和y上的以下双积分来计算每个xy横截面的平均值:
\int \int c(x,y,z) \,\mathrm{d}x \mathrm{d}y
其中 ,A(z)是横截面面积。
在 COMSOL 多物理场仿真软件中,你可以使用两个投影耦合算子来计算此双积分。第一个算子通过x积分从 三维投影到 二维(y方向在这里同样有效)。第二个算子通过在剩余坐标上进行积分,将第一个算子的结果从二维投影到一维。
如果几何图形包含yz平面中的平面,那么设置算子最为简单。如果不是这种情况,至少有三个选项:可以修改组件的几何形状,但随后必须重新计算解,如果模型需要很长时间来计算,这不是一个方便的选项;可以使用广义投影算子来代替;或者,可以为平面添加另一个具有二维几何图形的组件,并将从三维组件投影到二维组件,这可能是最简单的选项。这是可行的,因为源和目标不必属于同一模型组件。如果使用第三个选项,则可以对解运行更新,而不必重新计算所有内容。
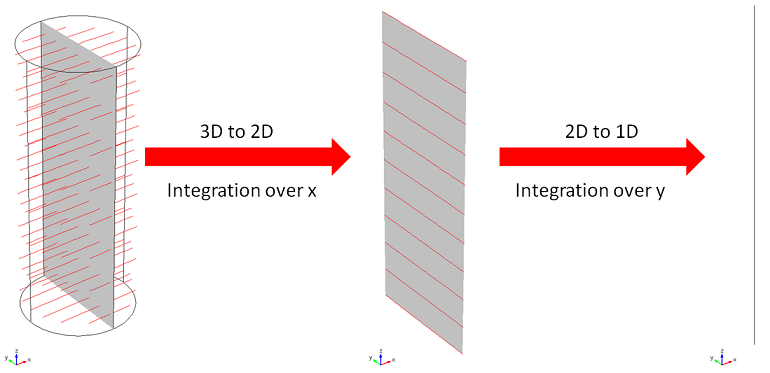
双积分由两个投影算子执行。红线表示积分线。
结束语
在这篇博客中,我们演示了如何使用投影算子来分析仿真数据。如果适用,这项技术可用来提炼结果的本质,并帮助你更深入地了解底层物理。如果你对了解有关使用投影算子的更多信息感兴趣请与我们联系。



评论 (0)