多物理场仿真助力分析小提琴的音调与音量

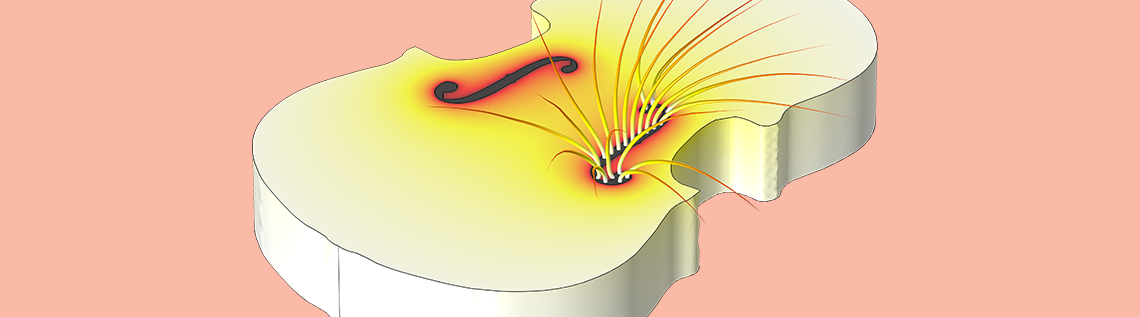
从 10 世纪到 18 世纪，小提琴的音孔从圆形逐渐演变为细长的f形。在最近发布的一篇研究论文中，美国麻省理工学院的科学家和波士顿北本尼特街学校（North Bennet Street School）的小提琴制造商研究了这种形状变化对音质的影响。他们认为 f 形孔能够增强气流，将小提琴低音的响度增加两倍。今天，我们将使用 COMSOL Multiphysics 重现他们的研究结果。

小提琴背后的物理学

小提琴背后的科学与它们弹奏的音乐一般复杂多样。与小提琴相关的研究主题包罗万象，从运弓的生物力学，到被蒙住眼睛的出色小提琴家能否辨认出正宗的斯特拉迪瓦里（Stradivarius）和现代小提琴（剧透：他们不能）。

一把小提琴。

同麻省理工的研究人员一样，我们的研究重点是 280 至 300 Hz 附近的基本空气共振模态。在较高的频率下，小提琴主要靠琴身振动来增强声音，但在这个频率下，小提琴内的空气会产生共鸣。因此，低音音符的大部分声音是通过 f 孔发射出来的。

作为一次近似，该空气模态通常被视为完全发生在空气中的亥姆霍兹共振。研究小组在实验中引入了模拟和测量方法，试图弄清小提琴琴身的振动如何影响共振频率。您或许好奇控制琴身振动需要哪些实验条件，请不要担心——没有必要特意使用混凝土制作一把小提琴。该团队巧妙地将普通的小提琴固定在合适的位置上，几乎能消除所有振动。

当然，借助 COMSOL Multiphysics 模型，这种类型的实验可以变得更简单。建立声-结构相互作用模型后，共振将自动耦合到实体上。然后禁用结构，便只留下空气振动。我没有适用于此模型的小提琴 CAD 文件，因此创建了一个相当逼真，但不至于太复杂的原始几何。在线搜索了小提琴的构造图后，我决定创建一个如下图所示的几何结构。

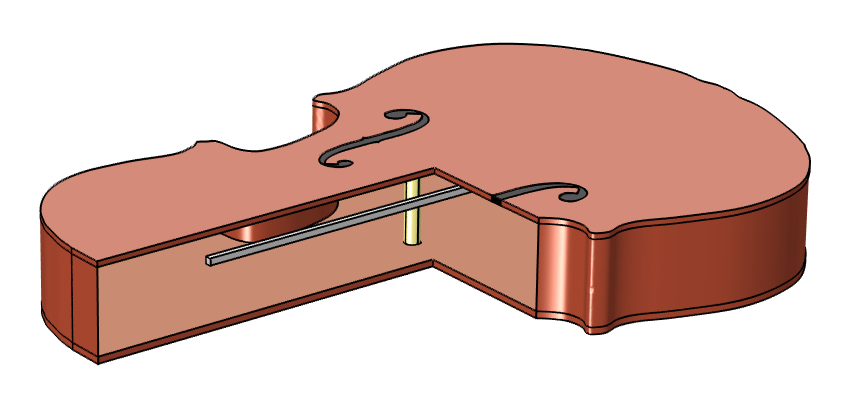
小提琴的模型几何，包括平坦的顶板和底板、刚性侧面、f 孔（黑色）、固定在顶板下的加固低音梁（灰色）和连接上下板的音柱（黄色）。

我没有试着重新创造一把属于某个品牌的小提琴，而是徒手勾画了琴身和 f 孔，并将其缩放到小提琴实物的标准尺寸。小提琴琴身的侧板通常非常坚硬，应该不会主动影响共鸣，所以被模拟为硬声场边界。对于琴身的其他部分，我采用了杨氏模量为 10 GPa 的云杉材料。

定音调：模拟声-结构相互作用

下图显示了压力声学的计算结果，其中整个琴身被设为声学刚性。颜色标度表示小提琴内部和f 孔内的声压级。我们在小提琴外添加了空气半球的轮廓，目的是让模态自由衰减，而不是在孔的正上方被人为地切断。此分析得到的特征频率为 304 Hz。

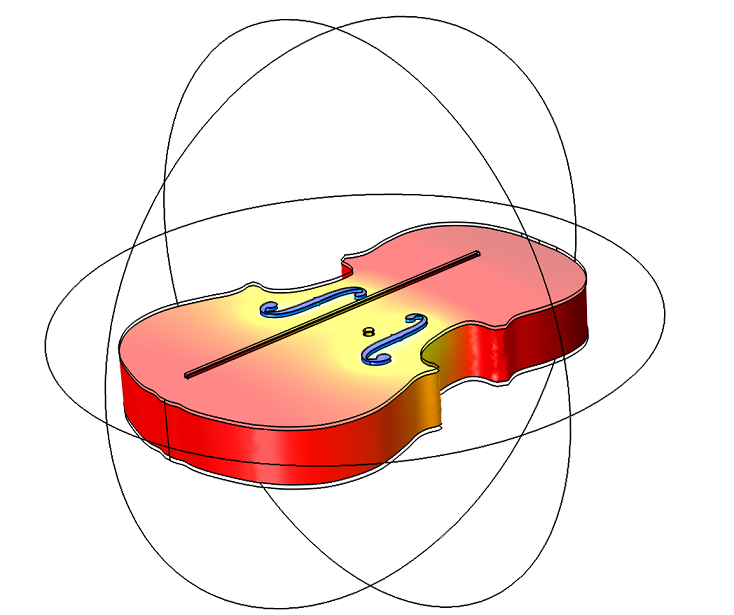
空气共振模态的压力声学计算结果显示了声压级分布，频率为 304 Hz。声压级范围从蓝色（低）升高为红色（高）。我们计算了各处的声压级，但隐藏了外部空气中的分布。

通过添加上述结构，我们增加了系统的灵活性，同时期望特征频率会降低。这正是模型中所发生的情况。虽然声学模态的基本形状（图中未显示）仍基本相同，但是顶板和底板现在开始充当弹簧，进而增加了系统的柔度。正如下图所示，顶板和底板都向外弯曲，以适应腔体内的压力。这将特征频率降低到 287 Hz。

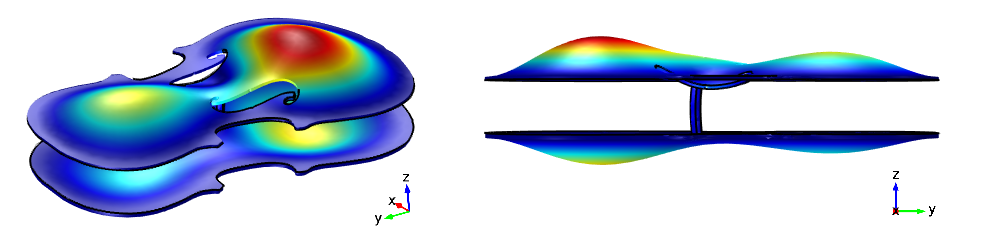
在腔体承受最大压力的阶段，小提琴体变形的四分之三侧面图和侧视图。特征频率目前降到了 287 Hz。

在计算中增加实体导致特征频率降低 17 Hz（6％），这与研究人员的发现相当一致。他们曾使用真正的小提琴来做实验，报告显示自由状态和受钳制状态下的特征频率均略高于我们的仿真结果。然而，6％ 的差异是相同的，这支持了团队提出的两者之比对乐器细节相对不敏感的观点。既然得到清晰的结论，您便可以在此确认：6％ 的特征频率下降是一个完整的半音。如果要好好给乐器调音，就需要考虑到声-结构相互作用！

定音量：模拟气流

回顾一下本文开篇时提出的主要问题：音孔形状会产生什么影响？该研究论文讨论了无限大的硬声场表面上各式音孔的解析结果和模拟结果。如果我们想要将音孔形状变化与长期以来的其他设计变化带来的影响区分开，这种理想化方法当然是个好主意。不过，既然我们建立了小提琴的模型几何，不妨利用这些信息找出音孔形状对音量的影响。

研究人员想出了一个相当简单的气流模型：在无限硬声场表面（此例为小提琴）外的空气中求解势流方程。至于边界条件，将音孔表面的势函数设为常数值，并将无限远端的势函数设为零。然后对从音孔中的总通量进行积分，即可测量气流的相对大小。

COMSOL Multiphysics 的可压缩势流接口可以求解与论文中相似，但更高级一些的方程。我们将零势函数条件应用到小提琴周围的空气球体表面。为保证一致性对比，圆孔面积必须与 f 孔完全相等。

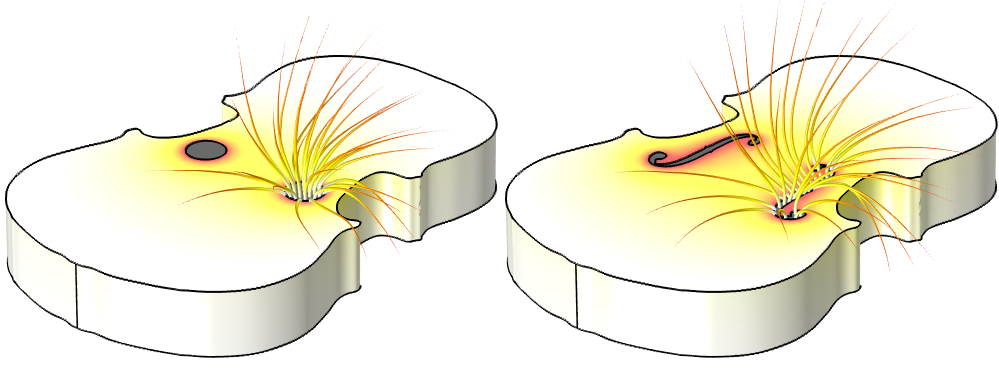
圆形和 f 形音孔上方的速度势分布和空气流动。绘图仅显示其中一个孔的流动情况。

不同几何形状的流量比为 1.51，这对 f 孔更加有利。若我们假设声功率与流量的平方成正比，则小提琴音量的最大比值为 1.51²= 2.28。但是该比值却大于论文所述的比例因子——2。这次模型结果是否达到了目标？事实再次证明，没有实体振动和没有实体传输的默认假设并不完美。根据研究小组估算，真正的、具有柔性的小提琴在空气共振模态发出声音的情况下，更加接近计算出来的气流，此时指数为 1.7。我很乐意为了探究该命题再建立一个模型。但就目前而言，1.51^1.7= 2.01 ≈ 2 足以令我满意。

了解更多使用 COMSOL Multiphysics 模拟乐器的知识

• 亲手操作：下载“小提琴中的声-结构相互作用和气流”教学模型
• 阅读本文中讨论的研究论文：H.T。“The evolution of air resonance power efficiency in the violin and its ancestors,” The Royal Society, 2015.
• 阅读介绍鼓面的数学建模的博客文章