
手机、电子书阅读器、计算机,甚至腕表类的消费电子产品中都用到了触摸屏技术。大量触摸屏中都用到了某种形式的电容传感。让我们来看一下如何使用 COMSOL Multiphysics 的 AC/DC 模块来分析这类电容传感器吧。
电容传感简介
对于诸如触屏设备中用到的电容传感器,其中包含了大量内嵌在透明介电材料(比如玻璃,甚至蓝宝石屏幕)中的导电电极。这些电极本身非常薄,由几乎完全透明的材料制成,且对裸眼不可见。
让我们先从一个非常基本的结构开始,其中包括两个以 90° 角交叉放置的电极阵列,如下图所示。
请注意实际的触摸屏要比我们这里所看到的更复杂,不过模拟技巧基本相同。
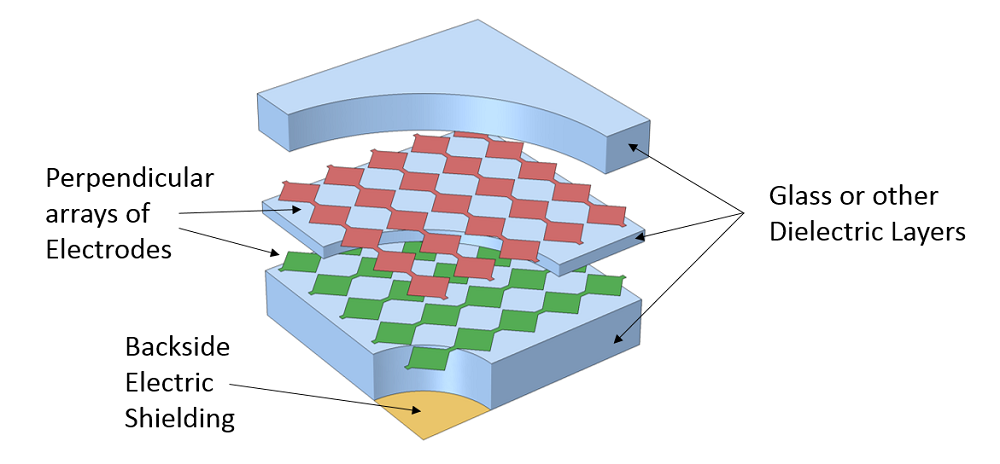
电容触屏传感器中核心部件的简化示意图(非等比例)
当向任意两个或更多电极之间施加一个电压差时,就会产生静电场。虽然静电场在电极之间和环绕电极的区域最强,但它还是会向外延伸一定距离。当导电物体(比如手指)接近这一区域时,电场就将发生改变,从而能够检测到两个主动电极间合成电容的变化。我们正是通过该电容差来传感正在触摸屏幕的手指位置。
当向部分电极间施加一个电势差时,其他电极可以是单独电绝缘,或是在电学上连接为一个整体,但仍处于电绝缘状态。因此,它们可以有一个恒定但未知的电势。
能否正确模拟这些电极、环绕金属壳,以及其他介电物体,是计算电容变化的关键。让我们来看一下如何使用AC/DC 模块的功能来实现这一点。
模拟腕表中的电容传感器
对于这样一个相对较小的设备,我们可以模拟整个结构;传感器的尺寸仅为 20 * 30 mm,两个电极之间的间距为 1 mm。对于更大的触摸屏,更合理的做法是仅考虑整块屏幕中的一小块区域。

内嵌在玻璃表盘(透明)中的电容传感器。表带和表壳仅用于可视化目的。
如下图所示,模拟域为圆柱形区域。该区域包含了玻璃屏、手指以及手表周围的空气。我们有理由认为周围空气尺寸的影响会随着尺寸的增大而迅速减小。
所使用的边界条件
在这里,空气域的边界被设定为零电荷条件,以将边界模拟为自由空间。此外,平行电极中的两个设定为接地边界条件,电压场固定为零。垂直电极中的两个设定为终端边界条件,电压为恒定值。终端边界条件将自动计算电容。其他所有边界都通过悬浮电位边界条件模拟。
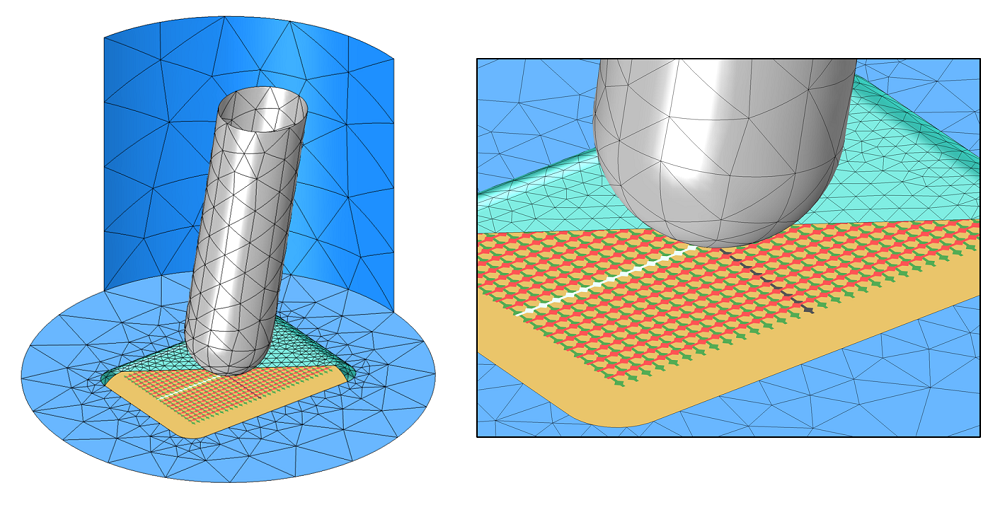
可视化有限元模型。手指(灰色)、电屏蔽(橙色),以及所有未激励的电极(红色和绿色)均通过悬浮电位边界条件模拟。在两个电极(白色和黑色)上施加了电势差。部分表盘(青色)被隐藏。其他所有面则使用了电绝缘边界条件(蓝色)。空气和表盘进行了体网格剖分。为清楚起见,仅显示了部分表面上的网格。
悬浮电位边界条件用于表示电荷可自由重新分布的一组表面。设定的目的是为了模拟拥有恒定但未知电势的物体边界。这是在外部施加静电场的结果。
几组面上使用了这类悬浮电位边界条件,比如手表的底面,它代表了玻璃壳下的电屏蔽。当前未被激励的电极是单独的悬浮电位边界条件中的一部分(假定所有电极在电学上连接在一起)。注意,可使用悬浮电位组选项来允许每个物理上独立的边界浮动到不同的恒定电压上。也可以将任何组合的电极通过归入相同的组来把它们在电学上连接在一起。
手指边界(包含在模型中时)也使用了悬浮电位边界条件。假定相对空气和介电层,人体相对来说是良导体。
所用材料
这里只用到了两种不同的材料。大部分域中使用了预置空气材料,介电常数设定为 1。屏幕使用了预置石英玻璃材料,以给予它较高的介电常数。
虽然屏幕本身是由不同材料组成的三明治状夹层结构,我们可以假定所有层都有相同的材料属性。因此,无须明确模拟它们间的每个边界;所有层都处理为一个单独的域。
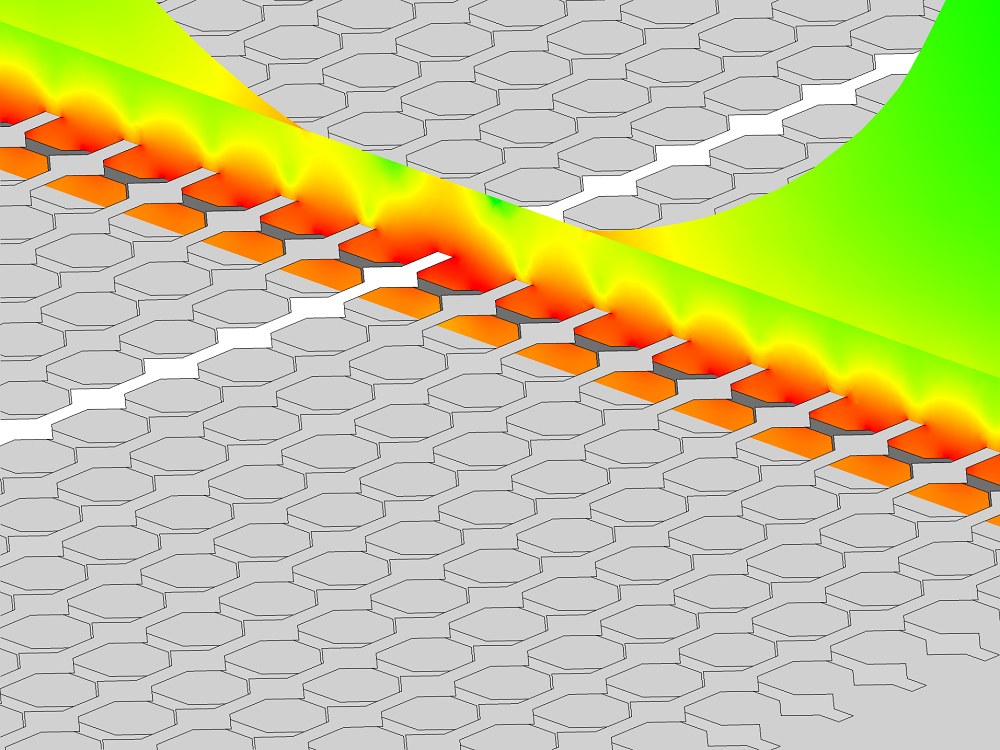
对电场值对数的颜色可视化。由于手指看作悬浮电位,其内部电场可忽略。
使用自适应网格细化所获得的精确解
要获得精确的结果就要有足够细化的有限元网格,以解析电压场的空间变化。虽然我们计算前不知道电压场中最剧烈的变化将出现在哪里,但可以通过自适应网格细化来让软件自行决定哪里需要更小的网格单元。
我们使用了几次自适应网格细化,结果如下表所示。这些结果是在配置有 3.7 GHz 八核至强处理器、64 GB 内存的计算机上得出的:
| 自由度(百万) | 所用内存(GB) | 求解时间,不含网格重新剖分(秒) | 电容计算值的百分比差异 |
|---|---|---|---|
| 0.125 (缺省“标准”网格设定) | 1.7 | 10 | 28% |
| 0.6 (第一次自适应网格细化后) | 2.2 | 20 | 6% |
| 2.3 (第二次细化) | 4.8 | 84 | 2% |
| 7.7 (第三次细化) | 14 | 711 | 0.6% |
| 24.4 (第四次细化) | 47 | 2,960 | N/A |
从上表可以推断出,我们可以从一个非常粗化的网格开始,然后使用自适应网格细化来得到更精确的电容值。不过,这样做会增加内存使用并延长求解时间。电容百分比差异针对的是网格最细化的情况。
计算电容矩阵
到目前为止,我们只关注了阵列中两个电极间电容的计算。实际上,我们希望能计算电容阵列中所有电极间的电容,即电容矩阵。该对称方阵定义了系统中所有电极上所施加电压和电荷之间的关系。对由n个电极和一个接地组成的系统,矩阵为:
矩阵中对角分量由积分所有域中的电能密度计算得到:
其中
非对角项由以下公式给出:
其中
这些对角和非对角项由软件自动计算得到,这部分内容将在后续博文中更详细介绍。
小结
我们研究了利用 AC/DC 模块的静电模拟功能来求解电容触摸屏设备的示例。虽然这里出于介绍目的简化了几何,但所介绍的技巧也适用于更复杂的结构。
当求解这类有限元模型时,对所求物理量收敛性的研究非常重要(在本例中,通常为电容相对于网格细化的情况)。自适应网格细化功能极大提升了该模型验证步骤的自动化程度。
求解这类大型模型时,您也可以通过分布式并行内存求解器来获得更快的求解时间。当然,COMSOL Multiphysics 及其 AC/DC 模块的功能并不限于文中的介绍,您可以使用它来实现更多的功能。如果您希望了解更多内容,欢迎联系我们。



评论 (0)