
您有没有注意到,在一个快乐、热情的朋友身边,您也会感到非常快乐呢?您可以用类似的方式来看待互感:即某一电路中有电流通过时,会在附近的电路中产生感应电流。互感系数用来衡量这种电流感应效应变化的量级。在这篇文章中,我们将探讨使用模拟计算来估算不同线圈中产生的互感。
互感和感应电流
当一个随时间变化的电流流过电路(该电路被称为初级电路或初级线圈),会产生一个变化的磁场。磁场随时间变化,并会在附近的另一个线圈(被称为次级线圈)中,诱导产生电流。这种效应被称为互感。在变压器、电机、发电机和其他一些设备中,都要利用互感原理,因此对于这些设备的运行来说,互感是非常重要的。
您可能时常想知道,要在次级线圈中产生一个特定电压,初级线圈中的电流需要有多大的变化。为了解答这一问题,您可以通过计算一个线圈中电流的变化对另一线圈的作用,从而得到互感。计算互感还可以避免设备损坏,因为互感会引起导体之间不必要的耦合。
当计算互感时,线圈的方向、缠绕模式和两个线圈相互间的位置关系,都是非常重要的。如果两个线圈距离非常近,初级线圈产生的磁通量,几乎全部都会与次级线圈的每一匝相互作用,从而产生一个很大的互感。而彼此相隔很远的两个线圈产生的互感则小得多。线圈中如果存在磁性材料,互感也会增大。
让我们通过模拟几种不同排布方式的线圈,仔细看看这些因素是如何影响互感的。
利用仿真计算互感
两个单匝线圈之间的互感
在我们的单匝线圈示例中,初级电路是一个半径为 100 毫米的单匝线圈,次级线圈是一个半径为 10 毫米的单匝线圈。两线圈的横截面直径都是1毫米,排列方式为同心共面,用二维轴对称模型来模拟。两线圈被放置在一个无限元区域中。通入初级线圈的电流频率为 1 kHz、大小为 1 A。
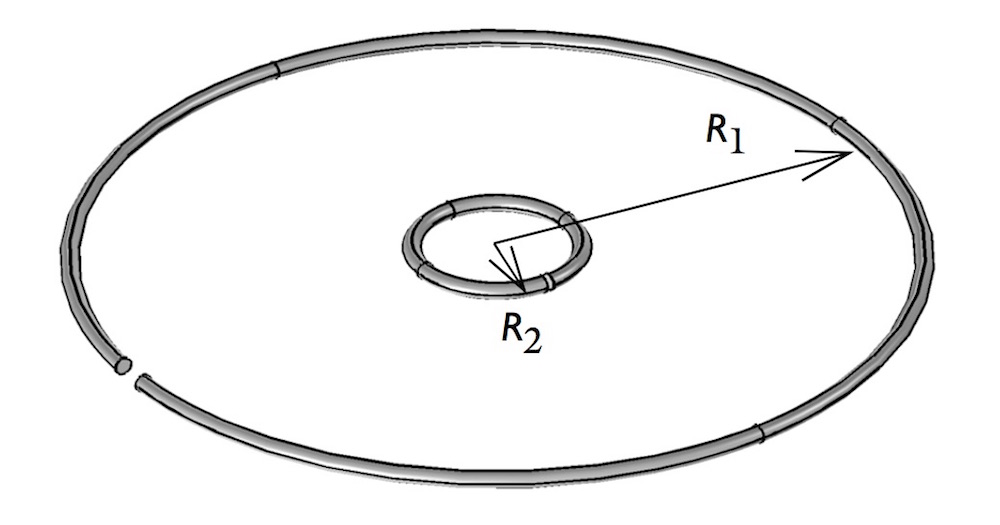
两个单匝线圈的排布方式。
我们利用单匝线圈的特点来模拟一个直流状态的线圈排布。由于初级线圈中的电流是恒定的(直流),它不能产生变化的磁场。因此,通过次级线圈的磁通量不会发生改变,这意味着不会在次级线圈中诱导产生电压。然而,通过分析总磁通,并将它与解析结果相比较,您仍然可以计算互感。然后,将该模型模拟为交流状态,以计算在次级线圈中产生的感应电流。
仿真结果给出了这种线圈的直流磁场分布,以及计算出的互感。
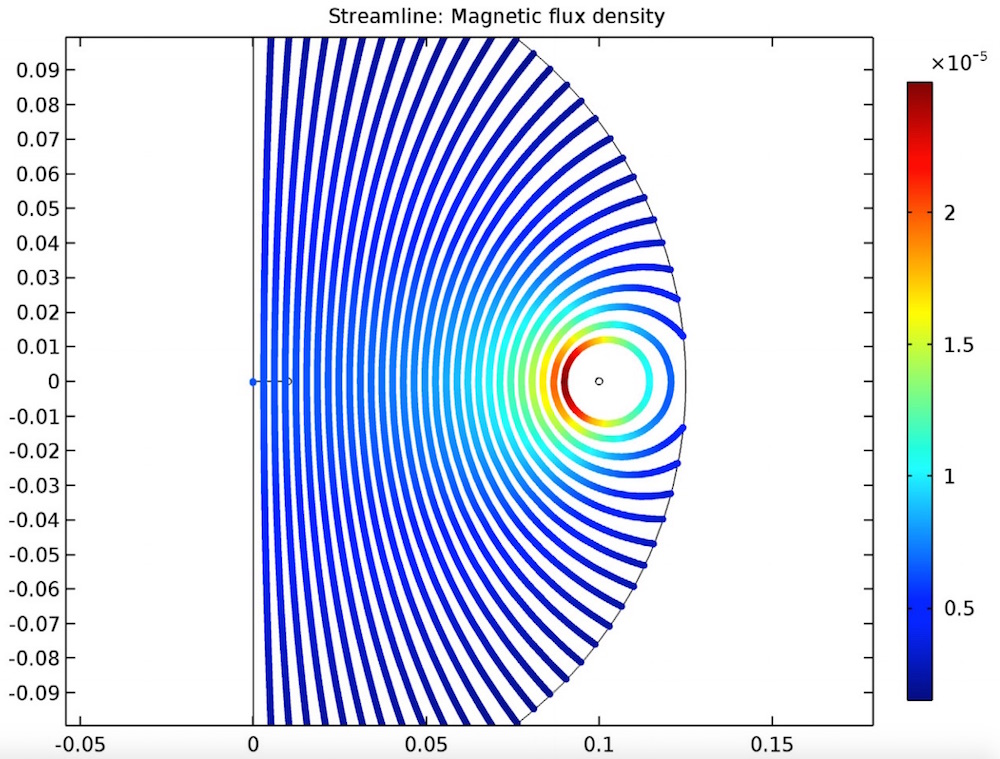
图中显示了直流模型的磁通量密度。
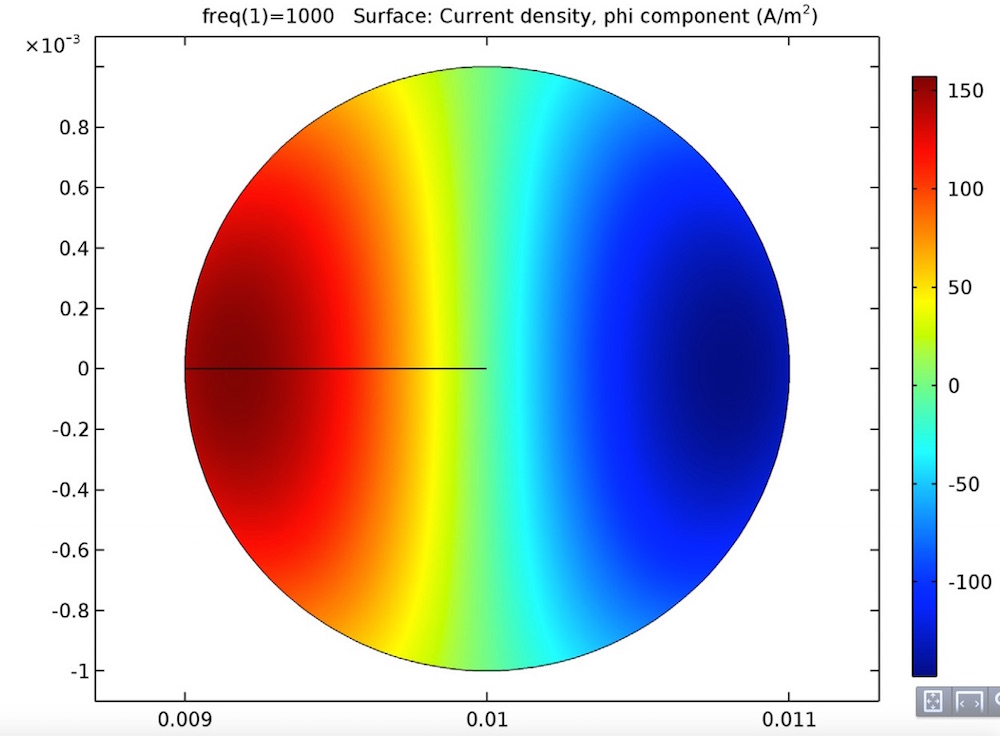
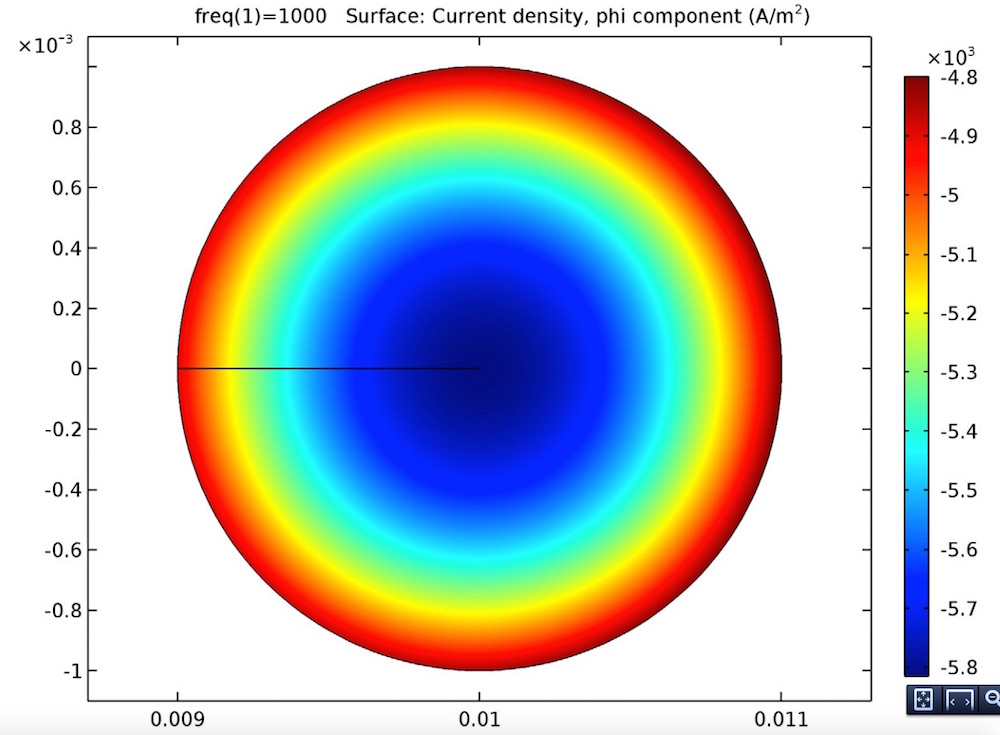
在开路(左图)和闭路(右图)单匝线圈中的感生电流。
从结果中,你可以分析交流模式下的感应电流和直流模式下的电感之间的关系。
一个多匝线圈和一个单匝线圈的互感
我们可以继续用类似的线圈装置来模拟两种不同的变化。在这个例子中,初级电路是相同的单匝线圈,但次级线圈是一个二十匝线圈。我们可以计算这种模型在开放式和闭合式电路情况下的互感。
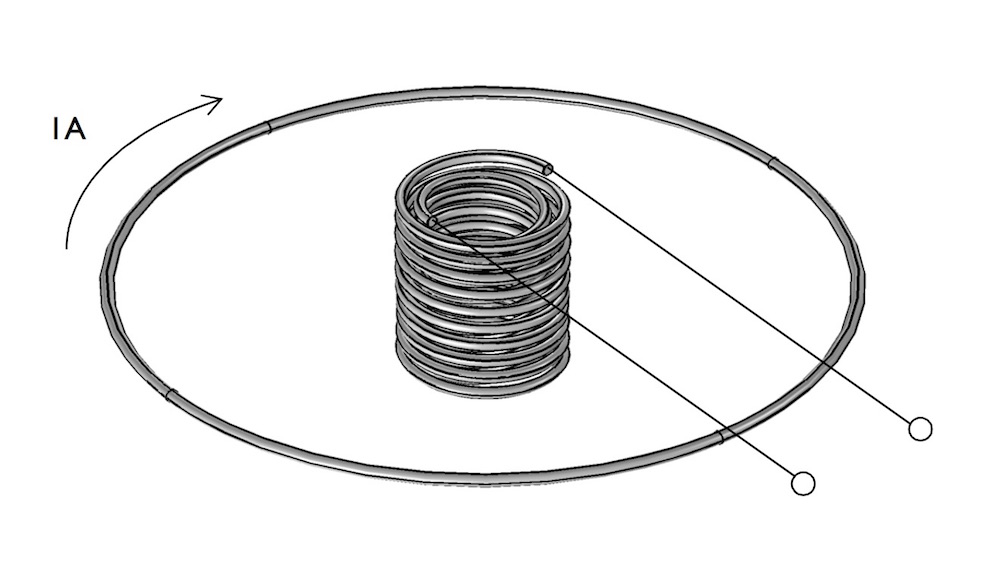
一个初级单匝线圈和一个次级二十匝线圈的排布方式。
对于这类多匝线圈示例,初级线圈利用单匝线圈的特性来建模,用作激励线圈。次级线圈以多匝线圈的特性来建模。在模拟次级线圈的匝数时使用均相的方法。
我们分别绘制了开放式和封闭式电路的磁通线,并计算了次级线圈两端的电压,从而可以利用这一物理量来找出互感。
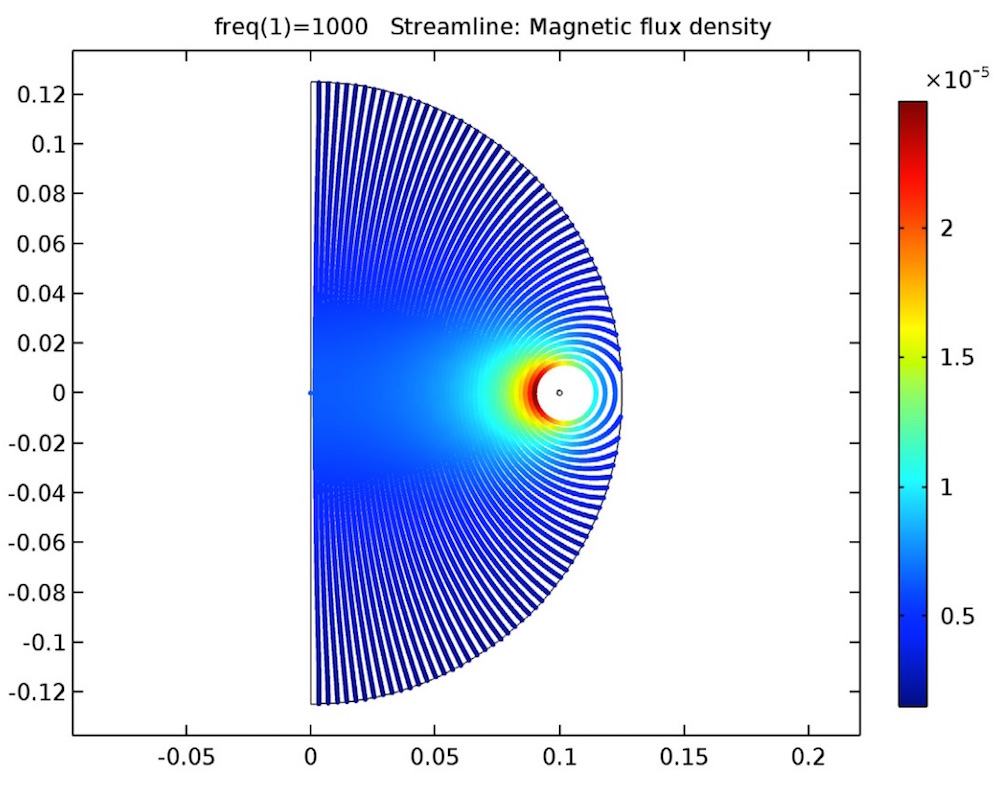
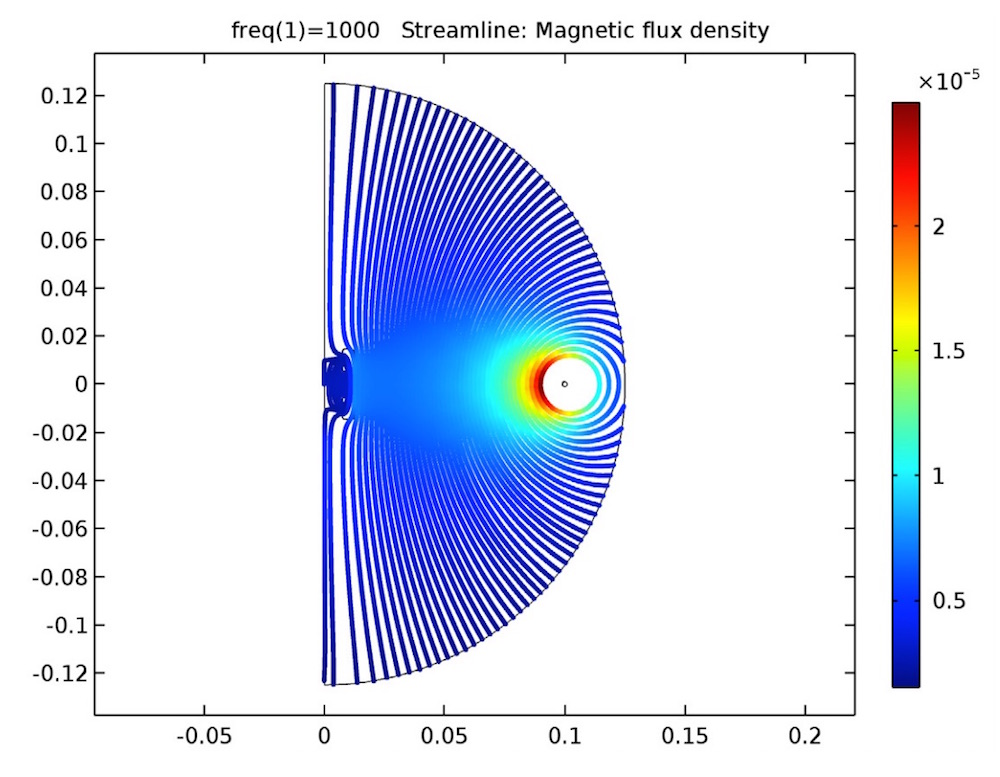
在开路(左图)和闭路(右图)多匝线圈中的磁通量。
同样排布方式的线圈也可以被建模,从而保证每个线圈的每一匝都被明确地建模。对于线圈组示例,初级线圈是利用单匝线圈的功能来建模。次级线圈也是利用单匝线圈的特性建模,但会增加一个附加的线圈组设置。这一设置的作用是,保证流过每匝线圈的电流相同,并计算出总线圈电压,从而找到互感。
通过增加附加设置得到的电压,由此估算出的互感,与分析数据吻合得很好。
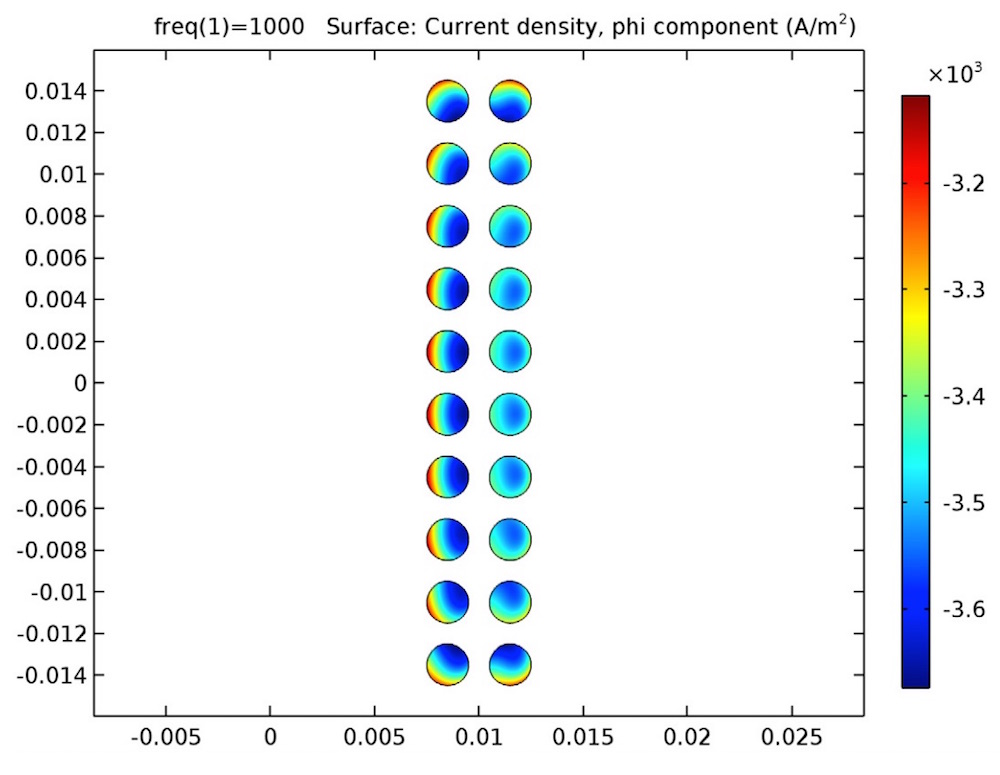
线圈组的磁通线(左)和感生电流(右)。
COMSOL Multiphysics 提供了一种简便的方式来计算多种不同的排列方式的电路的互感。想象将这一功能应用到您自己的模拟中的可能性。



评论 (1)
中会 郭
2019-05-22