由Edmund Dickinson创作的所有博客

蛋白质吸附:间歇式反应器和空间依赖性建模
研究系统的化学动力学时,通常会使用完全混合间歇式反应器假设,并使设计的实验一直保持理想的混合条件。这种假设包括完全混合(理想釜式反应器)和非完全混合(理想塞流反应器)。然而在实际应用中,反应器很难达到理想状态,因此空间依赖性建模对于理解和优化化学反应器至关重要。下面我们将详细探讨反应器模型的开发,先从一个简单的完全混合示例开始。
混合动力和电动汽车中的牵引力从何而来?
您可能会认为自己开车很稳,但您的发动机很可能并不这么认为。每天我们都要面临像信号灯这样的路障和变速限制,这意味着我们对汽车动力传动系统的动力需求变化很大。我们希望混合动力或电动汽车的性能可以与现代汽车相提并论,比如当频繁踩油门和刹车的时候。所以,设计人员需要能以一种安全的方式实现这类目标,这其中就涉及了对电池的模拟。

建筑中的多物理场仿真
设计新建筑时,建筑师们不仅要考虑它的艺术审美性,还要兼顾结构的牢固性,所以说,建筑师们不能仅仅是艺术家。在现代建筑设计中,人们非常关注环境是否舒适以及能源效率情况。从设计概念的提出到最终定稿,其间要解决一系列的物理问题,21世纪,建筑师们或许可以转向多物理场软件来获得帮助。
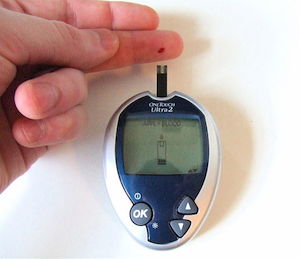
糖尿病管理的电化学建模
对于糖尿病这一全球性杀手,目前还没有有效治愈手段:据世界卫生组织估计,全世界范围内有 3.5 亿的糖尿病患者,年平均死亡率在 1% 左右。幸运的是,现代医学使糖尿病患者能够管理自身的葡萄糖水平和摄入量,因此在许多国家糖尿病的威胁已大为降低。多数糖尿病患者必须全天候监测他们的葡萄糖水平,这就需要有精确的方法来测量血液中的葡萄糖浓度。对于现代传感器的设计而言,电化学方法是一个很好的选择。

电流分布理论
在电化学电池的设计中,您需要考虑电解质和电极中的三种电流分布类型,它们被称作一次、二次 和三次电流分布。三种电流分布对应着不同的近似方式和程度,采用其中哪一个则取决于电解质溶液电阻、有限电极反应动力学以及质量传递的相对重要性。在本文中,我们将概述电流分布的概念,并从理论层面上探讨这一主题。

借助传递与固体力学耦合模型做出更美味的爆米花
在 COMSOL 工作期间,传热所能涉及的领域广度一直是我的兴趣所在。研究人员常常使用 COMSOL Multiphysics 进行食品制造中的传热研究,远非局限于钢锭和 CPU 风扇方面的研究。对爆米花生产过程中热力学效应的研究便是一个很好的例子,这个案例曾在 COMSOL 用户年会 2013 波士顿站上做过演示。
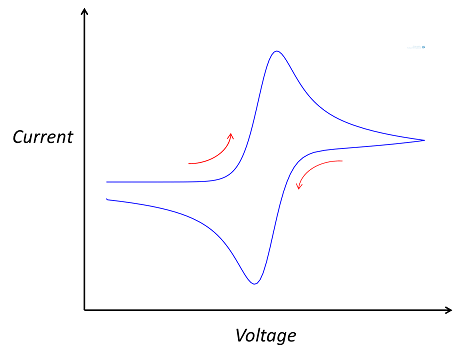
模拟电分析:循环伏安法
如果你不是电化学家,很有可能从未接触过循环伏安法。但是,当你去看任何一本电化学期刊、会议论文集或者电化学传感器制造商公司的网站时,会发现在靠前的位置总能看到一个独特的“双峰”图。 为什么要使用循环伏安法? 这个“双峰图”看起来像这样: 这是一个循环伏安图,绘制了电化学电池中电流随施加电压的变化而变化的曲线。通过在一定范围内扫描往返变化的电压,驱动电极的电化学反应朝不同方向发展: 循环伏安法是一种应用非常广泛的技术,用于检测电极与电解质(如盐溶液)界面的物理和化学性质。电活性表面在所有电化学装置中都很常见,包括电池和燃料电池等常见的能量提取装置,以及如用于监测糖尿病患者血糖浓度的电化学类传感器。然而,人们仍然没有完全理解电极-电解质界面的化学性质,这是一个活跃的学术研究领域。 伏安法对设备验证和设计很有价值,因为一次扫描就包含了关于系统的化学和物理行为的大量信息。此外,伏安法还是传感器运行的基本工作模式,因为在设计良好的系统中,测得的电流与分析物的浓度成线性关系。对电极材料进行化学修饰使得伏安法可专门用于检测混合物中的某种生物化合物或有毒气体,由于可以使用丝网印刷电极技术实现“一次性电化学”应用,因此它成为了一种成本低廉的先进技术。 对于设计和研究而言,伏安法的最大优势在于其提供信息的多样性。它阐明了电极表面的电解速率与反应化学物质通过扩散到达该表面的传输速率之间的竞争关系,还能提供有关溶液中化学反应的机理和速率的宝贵信息。在不同的扫描速率下使用伏安法,改变了电压随时间的变化速率,我们可以观察到不同系统时间尺度下不同的物理现象。 为什么模拟伏安法? 尽管伏安法非常重要,但却是一种理解起来有些困难的技术。系统中所有真实的物理效应都被归结到一些非常晦涩的电流-电压曲线中,虽然经验丰富的电分析化学家可以直观地从伏安图中“看到”化学反应,但要从实验中获得定量信息,就必须将伏安法与理论预测结果进行比较。由于电化学动力学通常是非线性的,而伏安法又是一个瞬态问题,理论上不太可能获得解析解(极少数特殊情况除外),因此必须进行计算机模拟。 保持模型的简洁性 COMSOL 的电化学模块包括一个电分析 接口,专为模拟伏安法等电分析技术而设计。其中假定存在大量的支持电解质,例如,人为地添加到电化学电池的电解质中的惰性盐(如氯化钾),用于增加其导电性。支持电解质可减轻电场,其优势在于可以简化实验分析和基础理论。我们假定只有扩散对化学物质的传递起作用,因为溶液没有搅拌,而且时间尺度足够短,溶液中的自然对流不重要。在这些条件下,化学物质传递方程是线性的,因此更容易求解。 在伏安法实验的典型持续时间内,物质扩散的尺度非常短,通常远小于 1mm。对于半径超过 1mm、形状像圆盘的传统“大电极”,可以准确地假设扩散只在电极表面的法线方向比较显著,电极边缘的影响可以忽略,因此整个电极表面的反应和传递是均匀的。因此,伏安分析可以简化为一维瞬态问题。 设置循环伏安模型 为便于定义瞬态外加电压及其对电解反应速率的影响,电分析 接口包含一个预置的“电极表面”功能,可直接设置伏安法的电位窗口和扫描速率,它会自动实现电极动力学的 Butler-Volmer 方程,但与 COMSOL Multiphysics 中的其他很多功能一样,用户也可以自定义动力学表达式。然后,相关的循环伏安法研究会使用适当的数值方法对瞬态扩散方程进行积分,自动求解相应的瞬态问题。使用“参数扫描”功能,我们可以在一次计算中研究一系列扫描速率。 查看结果 从上图中,我们可以看到在 1mV/s 到 1V/s 四种连续扫描速率下记录的仿真预测的 4 个伏安图,这些预测对应的实验持续时间从近半小时到一秒多一点。可以看到电流随着扫描速率的增加而增加,但伏安图具有相同的“双峰”。后者可以解释为,刚开始时电压无法驱动反应物进行正向反应,因此电流可以忽略不计。随着电压升高,反应加速,因此电流增大。但一段时间后,电极表面的反应会耗尽反应物浓度。这时,决定反应速率的过程发生变化,致使电流受反应物向表面扩散的控制,从而再次下降。反向反应也有类似的过程,当电压扫描回到起点时,生成物会重新转化为原始反应物。 电流密度随扫描速度增加的原因是,扫描速度越快,扩散层形成的距离越短。由于反应物浓度在较短的距离上快速变化为零,扩散通量较大,因此电流也较大。实际上,峰值电流应与扫描速率的平方根成比例:检查这个关系是对实验数据进行验证的常用方法,用于检查测量结果是否受到扩散以外的物理效应的干扰。 在设计传感器时,我们总是希望最大限度地提高电流,从而最大限度地提高灵敏度,因此这种分析有助于电化学电池和化学环境的实际设计。通过比较仿真预测的伏安图和实验测量结果,我们可以确定材料属性和其他可能未知的系统参数,如扩散系数和反应速率。 请尝试对上述动画进行比较,了解电流与不断变化的浓度曲线之间的关系。请注意电极表面(x = 0)的反应物浓度是如何随着电流的增加而趋于零的,一旦电极表面浓度为零,浓度梯度在扩散作用下降低,电流也随之降低。在第二次扫描中,电流被反向反应逆转,电极表面的浓度又恢复到其主体值。 进一步研究 由于电分析 接口将电分析仿真嵌入到 COMSOL Multiphysics 环境(一个功能强大、灵活的有限元方法用户界面)中,因此可以直接进行扩展。通过添加反应域条件,可以将电化学生成物的后续化学反应包括在内;我们可以建立同一过程的二维或三维模型,研究真实系统几何结构中的扩散情况;还可以进行多个伏安循环,或应用非标准电压波形;将反应物对流与流体流动进行耦合,可以研究流体动力电化学。我们还可以通过同一用户界面考虑一系列相关技术,如电位阶跃计时电流法和电化学阻抗谱法。 提示:查看 COMSOL 案例库中的电极循环伏安法模型。
