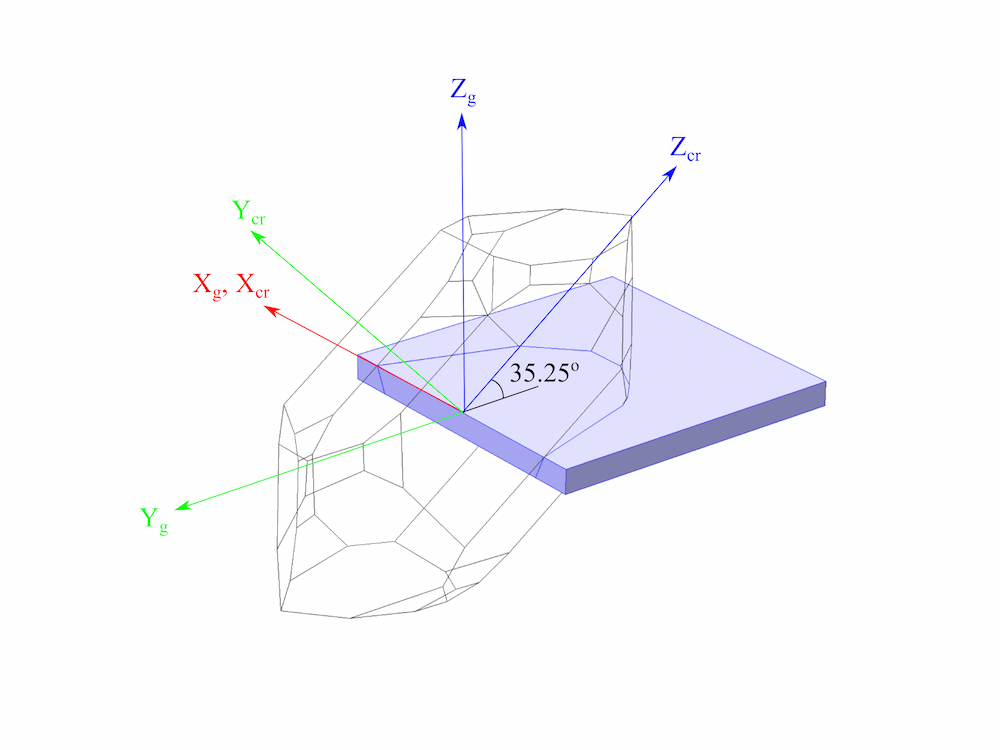
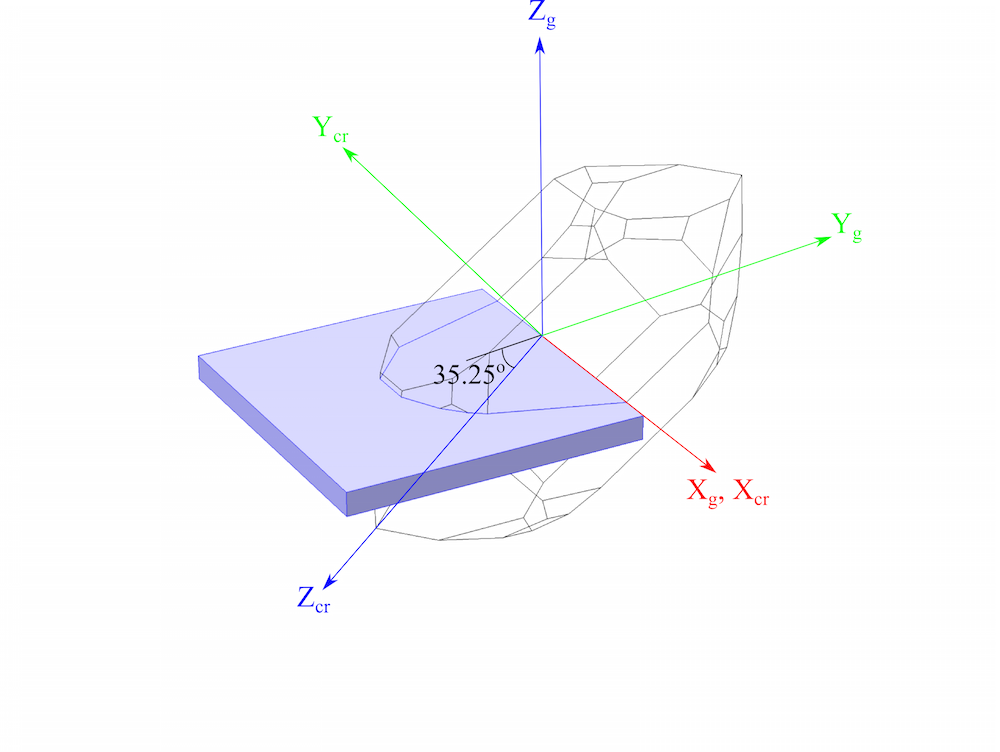
在上一篇博客文章中,我们详细介绍了用于描述压电材料的标准。COMSOL Multiphysics 支持两种压电材料标准:IRE 1949 标准和 IEEE 1978 标准。今天,我们将演示如何使用这两个标准设置晶体的方向,特别是 AT 切石英板的方向。
使用两个标准设置晶体的方向
要在 COMSOL Multiphysics 中设置晶体的方向,必须指定晶体轴与用于定义几何图形的全局坐标轴的方向相对应。这不同于标准中定义晶体取向的方式。因此,在定义几何图形的方向时需要小心。例如,如果板的方向改变,晶体轴的方向将随之改变。今天,我们将展示如何在实体几何中以不同的方向设置 AT 切石英板。
在上一篇博文中,我们详细讨论了 IEEE 1978 标准和 IRE 1949 标准中使用的系统。由于每个标准规定的晶轴方向不同,因此它们对 AT 切的定义也不同。下表显示了 AT 切的两种定义:
| 标准 | AT 切定义 |
|---|---|
| IRE 1949 | (YXl) 35.25 |
| IEEE 1978 | (YXl) -35.25 |
标准之间的差异可以通过从晶体切割的板所具有的由 l–w–t 轴集(l–w–t代表长度、宽度和厚度)定义的方向不同来解释。切割定义中括号内给出的前两个字母 -Y 和 X- 定义了最初与 l 轴和 t 轴对齐的晶轴。然后,围绕 l– 轴旋转 35.25°。标准之间的旋转方向不同,因为材料属性是相对于不同标准内的轴组定义的。我们可以看下图,它显示了围绕 l– 轴的转向对于 1978 年的标准( IEEE 1978)来说是正向的,但是对于 1949 年的标准( IRE 1949)来说是反向的。
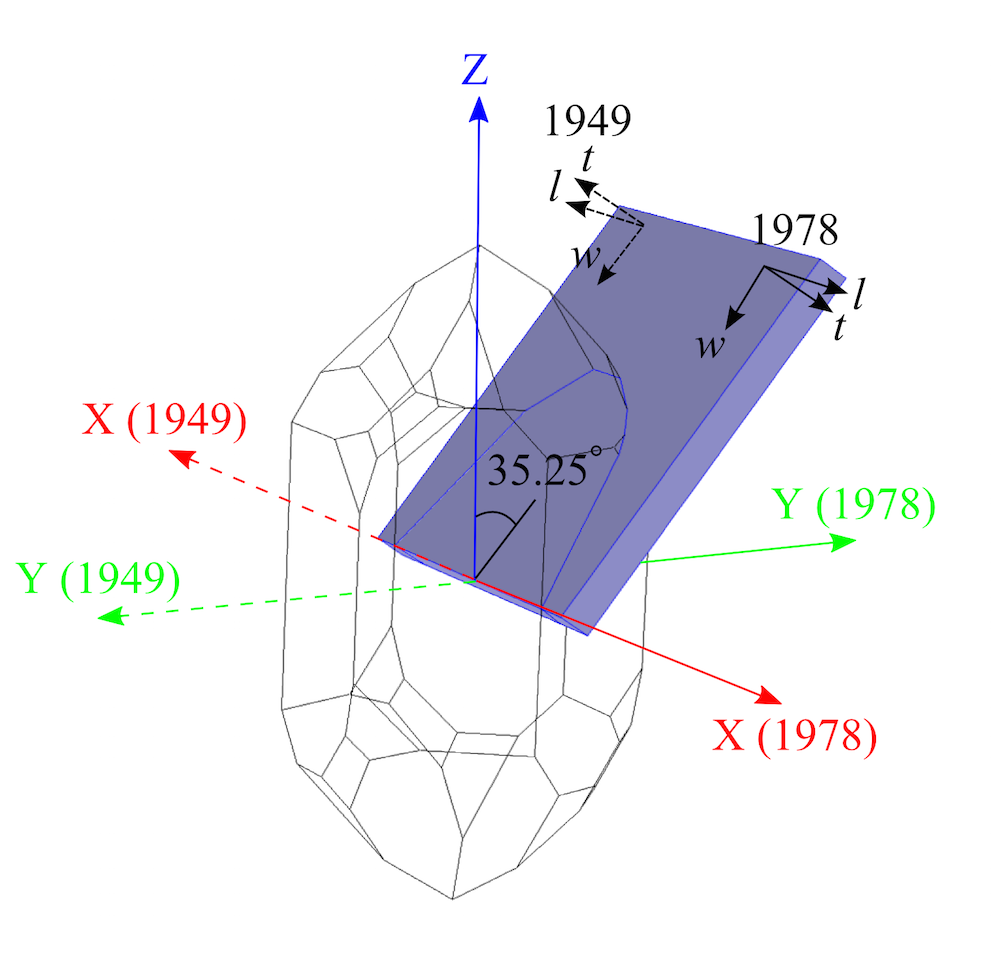
图中显示石英的 AT 切 (淡紫色长方体) 与右旋石英晶体。同时显示了由 IRE 1949 标准和 IEEE 1978 标准采用的轴组,以及板中 l–w–t 轴的设置。
这两种标准还有一个微妙的区别。由于在两个标准中定义了 AT 切,因此厚度和长度方向在两个标准之间是相反的(如上图所示)。从图中可以清楚地看出,要获得与 1949 年标准完全相同的板方向,1978 年标准需要围绕 w-方向额外旋转 180°。在这种情况下,1978 年标准中的 AT 切将被定义为: (YXlw) -35.25° 180°。在 COMSOL Multiphysics 中建立模型时,我们需要仔细考虑标准之间的这些差异。
全局坐标系
建立模型的一种方法是保持全局坐标系与晶体轴对齐,并简单地旋转板以与本文中的第一幅图对应。就像我们看到的一样,这种方法是完全可行的,只是它会导致几何形状的设置非常不便。
相反,我们将考虑如何定义 AT 切石英盘的材料方向。在这个 COMSOL Multiphysics 模型中,晶体方向由压电材料设置窗口中的坐标系选择决定。晶体方向通过用户定义的轴系指定,该轴系可在坐标系组合框中选择,如下所示。此示例基于简化版本的厚度剪切模式石英振荡器教程,您可在 COMSOL 案例库中找到。
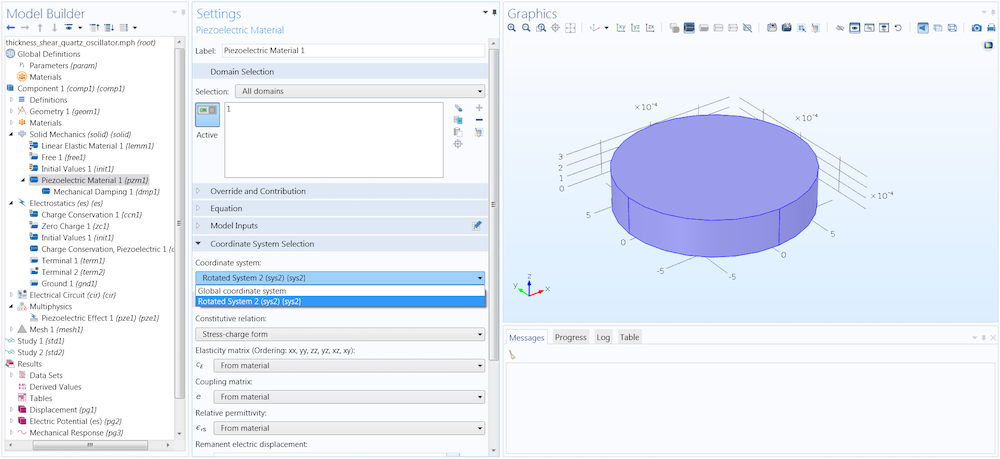
在 COMSOL Multiphysics 中更改压电材料的坐标系。
在上面的例子中,材料使用了1978年标准定义的左旋石英。如果我们希望使用全局坐标系来确定晶体方向,那么石英圆盘必须按照第一幅图中所示的方式进行定向,轴设置采用1978年标准。这可以通过使圆柱体绕 x 轴旋转来实现。
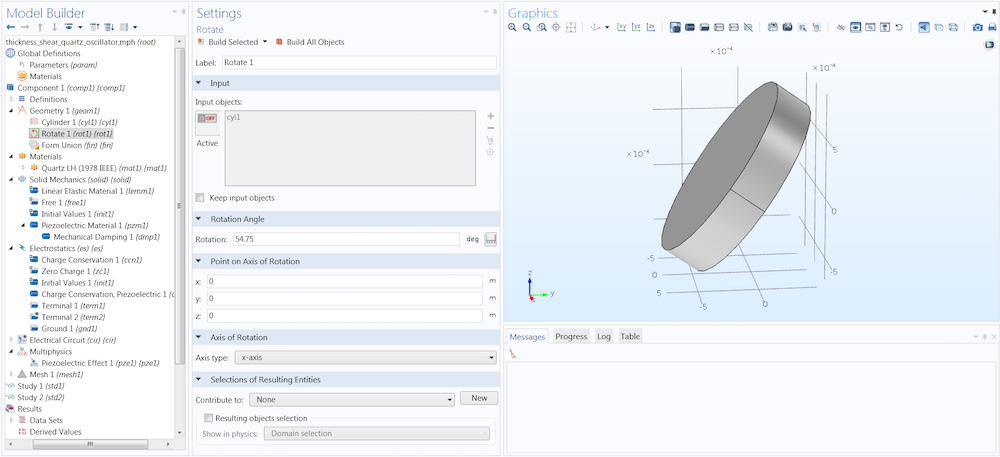
对石英圆柱体进行旋转操作。
下图显示了在不同选定方向设置时,设备的响应。晶体以厚度剪切模式振动。要获得此结果,您可以使用 COMSOL 案例库中的模型文件中的研究1,并求解单一频率 5.095 MHz。
| IRE 1949 标准 | IEEE 1978 标准 |
|---|---|
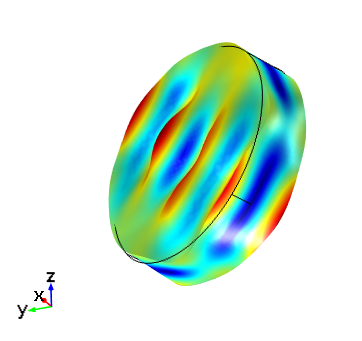 | 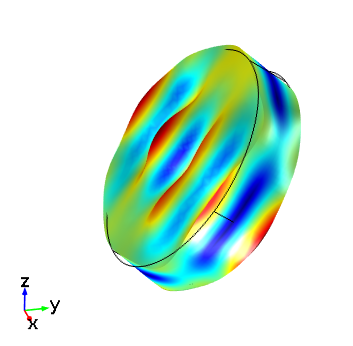 |
根据 IRE 1949(左)和IEEE 1978(右)标准设置的 AT 切晶体板的厚度剪切模式。驱动频率为 5.095 MHz。在这两种情况下,COMSOL Multiphysics 中的全局坐标轴与晶轴对应。
在 IRE 1949 标准中建立模型很简单,因为 COMSOL Multiphysics 在每个标准中都包含左旋和右旋石英的材料属性。要使用另一个标准,只需要将 Quartz LH (1949) 添加到材料模型中,并选择石英圆盘。这将覆盖先前添加的材料。然后,将圆盘的旋转角度改为-54.75°,以使盘的方向等同于第一幅图所示的板。如上图显示,按照这些步骤进行操作后,1949标准给出的结果与1978标准相同。虽然这两个图形看起来是相同的,但是全局坐标轴已被旋转,因此它们对应于第一幅图中的两个轴集。
如本例所示,可以将全局坐标系用于晶轴。但是,对于像AT切这样的切割,这将导致板在几何图形中出现非常用的方向。在实际应用中,一个模型中可能包含多个压电元件且具有不同的方向,则这种方法不能用于所有晶体。因此,通过旋转坐标系来指定晶体取向通常更为方便。
旋转坐标系
在 COMSOL Multiphysics 环境中,指定旋转坐标系最方便的方法是通过 Euler 角设置。给定晶体切割所需的 Euler 角,将根据板相对于模型全局坐标的不同方向而变化。现在,我们将考虑如何使用两个标准为不同的板方向指定 Euler 角。
给定标准中所需的 Euler 角的最佳确定方法是仔细绘制一个示意图,该图指定
l–w–t 轴相对于晶轴的方向。请注意,在 1978 年标准的一些图中,l,w 和 t 被标记为板的尺寸,而不是一组右旋轴系。在 COMSOL Multiphysics 模型中确定板的 Euler 角时,最好确保它们被绘制为一组右旋轴,以避免潜在的混淆。
Euler 角决定了相对于全局坐标系(Xg–Yg–Zg)的晶轴方向(Xcr–Ycr–Zcr)。因此,相对于全局坐标系的板的方向和晶体切割决定了Euler 角。
例如,我们将考虑 l–w–t 轴与全局轴 Xg–Yg–Zg 对齐的情况(对应于板,其厚度在 Zg 方向)。这通常是在较大的几何形状中定位板的最便捷的方法。下图显示了当我们采用第一幅图并且旋转该板,使得在这两个标准范围内,l, w,和 t 轴与全局轴Xg–Yg–Zg对应。为了便于与初始图形进行比较,两个标准中所显示的全局轴方向不同。
旋转后的石英 AT 切在 1949 年标准(左)和 1978 年标准(右)中,l, w,和 t 轴对应于全局轴 Xg–Yg–Zg 的图示。Y 和 Z 轴位于一个平面上。
下图显示了从第一幅图侧视方向查看未旋转和旋转的轴系。这个图表示了一个更简单的用“纸和笔”来确定 Euler 角的方法。
| IRE 1949 标准 | IEEE 1978 标准 | |
|---|---|---|
| 未旋转的轴方向 | 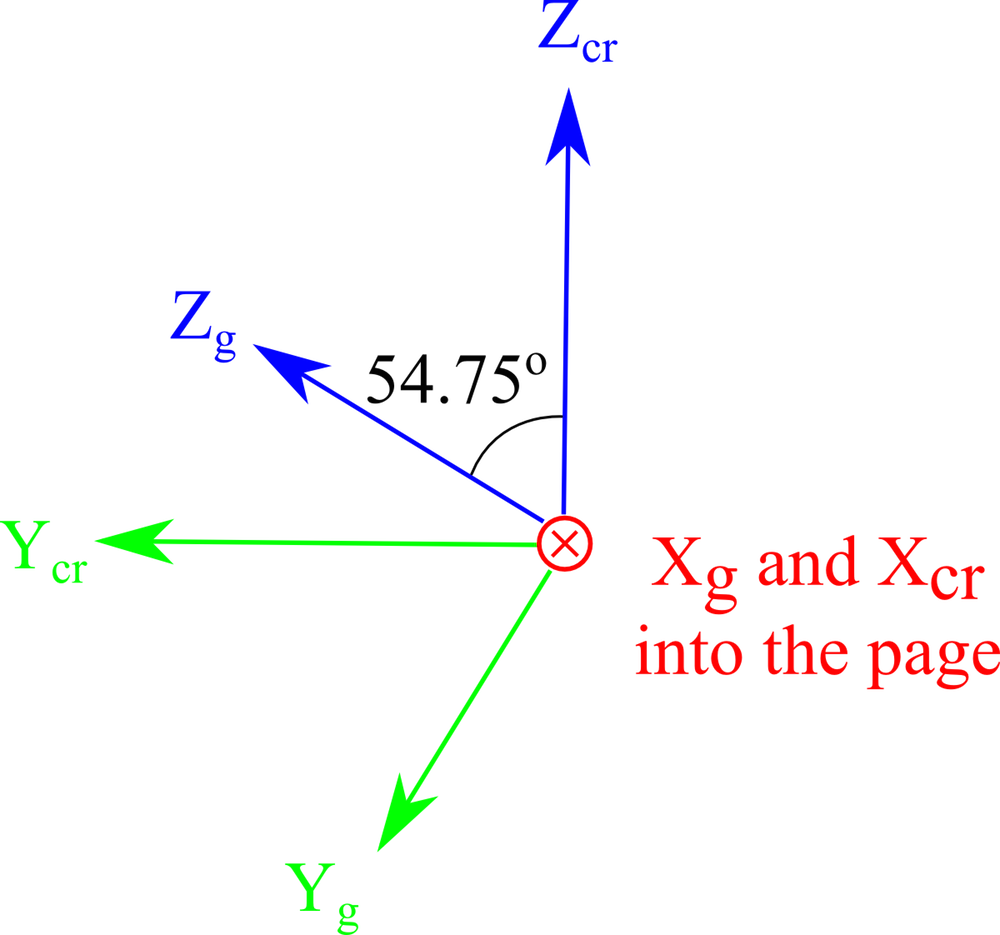 | 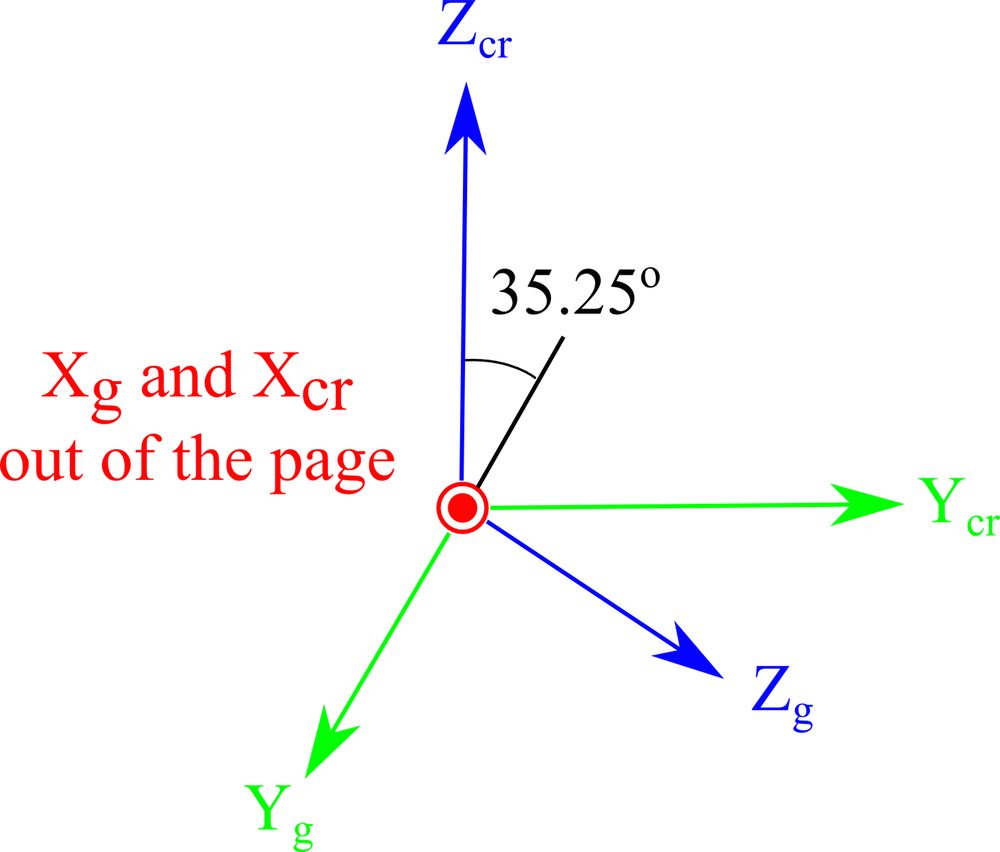 |
| 旋转的轴方向 | 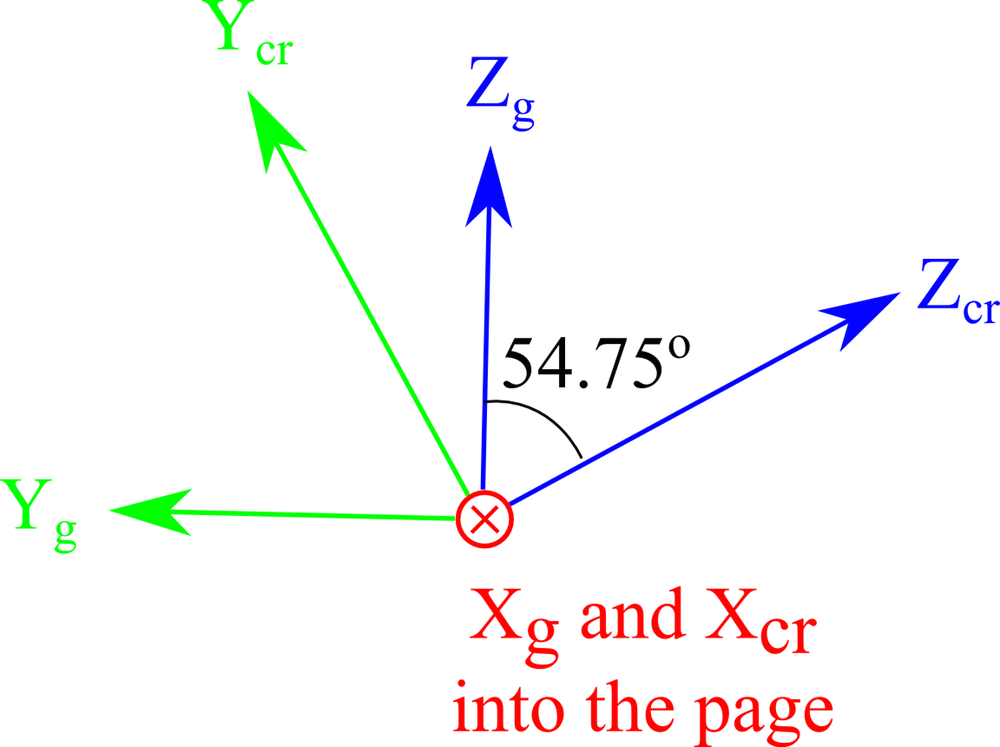 | 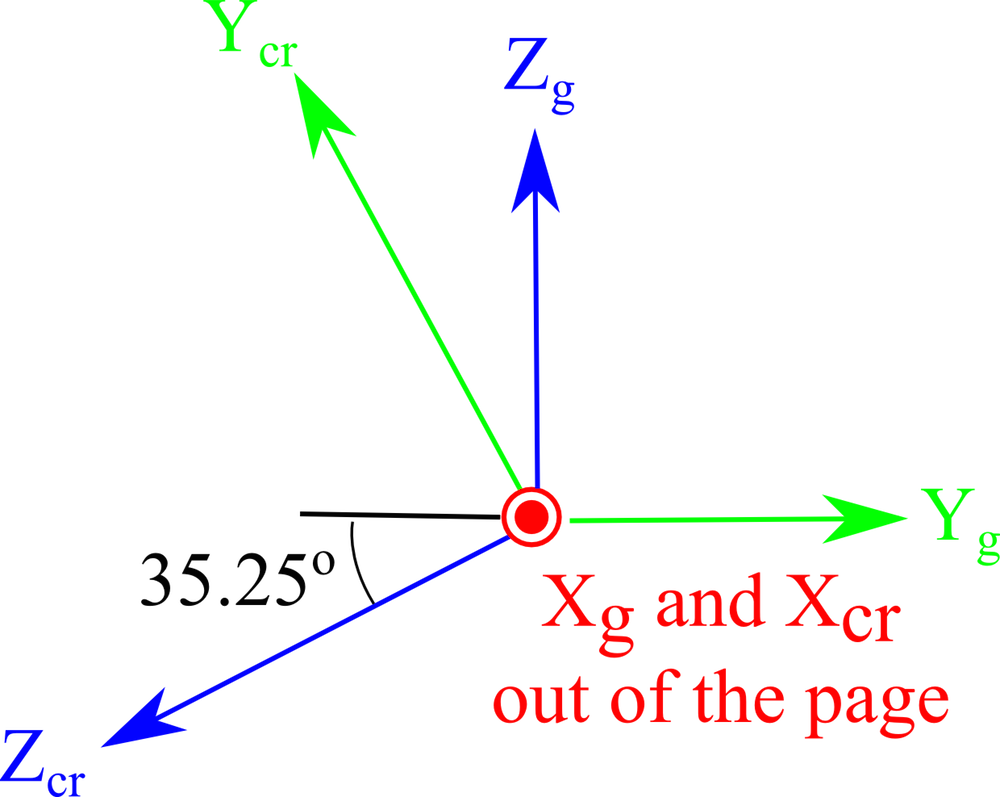 |
切割晶体时(顶部)和板轴平行于全局轴时(底部)的轴方向视图。
下图显示了如何在 COMSOL Multiphysics 中为旋转系统指定Euler角。任意旋转的系统可以通过先围绕 Z– 轴旋转,然后绕着 X– 轴旋转 (在下图中标记为 N),最后再绕 Z– 轴旋转。这就是所谓的 Z–X–Z 方案。
需要注意的是,对于通过多次旋转指定的切割,在指定 Euler 角时通常需要反向应用旋转。这是因为 COMSOL Multiphysics 软件指定了晶体相对于板的方向,而从晶体切割板所用的标准指定了板相对于晶体的方向。从上图可以直接获得等效的 Euler 角设置。
| Z | X | Z | |
|---|---|---|---|
| IRE 1949 标准 | 0° | 54.75° | 0° |
| IEEE 1978 标准 | 0° | 125.25° | 0° |
在两个标准范围中 AT 切的 Euler 角。绕 Z- 轴右旋的两个角度都是正的。
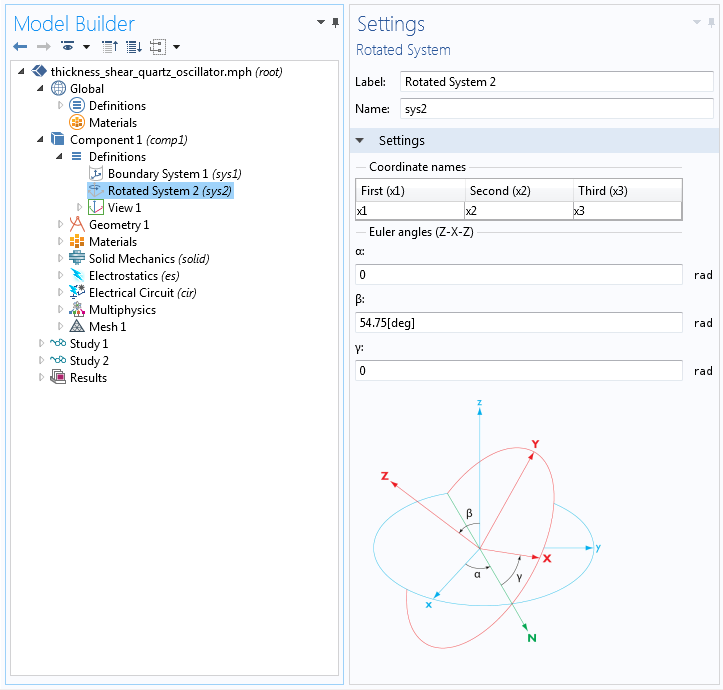
通过旋转坐标系特征使用 Euler 角指定坐标系。
如果我们使用上表中指定的 Euler 角来设置石英圆盘的厚度剪切模式,我们将获得具有相同激励和方向的两个板的结果如下图所示。哪里出了问题?问题在于,AT 切的厚度方向在两个标准内定义在相反的方向上。为了使用两种标准的模型获得相同的结果,我们可以切换驱动电极的极性,或者尝试使用上面提出的 1979 AT 切割定义:(YXlw) -35.25 180。作为最后一个练习,我们来考虑如何为这个双旋转切割设置 Euler 角。
| IRE 1949 标准: (YXl) 35.25° | IEEE 1978 标准: (YXl) -35.25° |
|---|---|
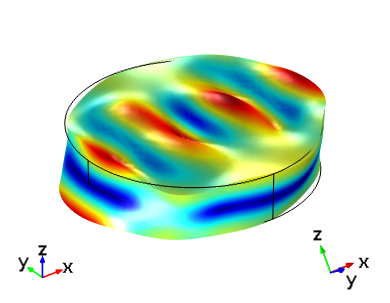 | 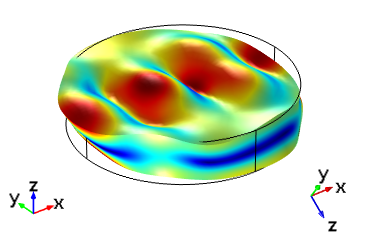 |
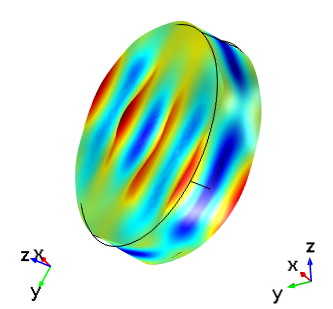 | 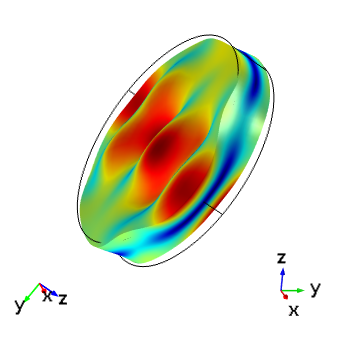 |
在驱动频率为 5.095 MHz 的情况下,根据 IRE 1949 和 IEEE 1978 标准建立的同一板的 AT 切晶体的厚度剪切模式。在每个图像中,左侧显示了全局轴方向,右侧显示了晶轴方向。顶部图像与全局坐标对齐,底部图像显示的晶体坐标与第一幅图中的方向相同。
下表中为涉及定义切割 (YXlw)-35.25° 180° 的旋转操作序列和将全局轴旋转到晶体轴上所需要的 Z-X-Z Euler 旋转序列。表中提供了相应的 Euler 角。请注意,Euler 角的旋转顺序与切割定义中指定的旋转顺序相反。
| IEEE 1978 标准: (YXlw) -35.25° 180° | |
|---|---|
| 1.厚度方向(Zg)沿晶体 y 轴(Ycrg)沿晶体 x 轴(Xcr)定向。 |  |
| 2. 将切割绕 l – (Xg)轴旋转 35.35°。 | 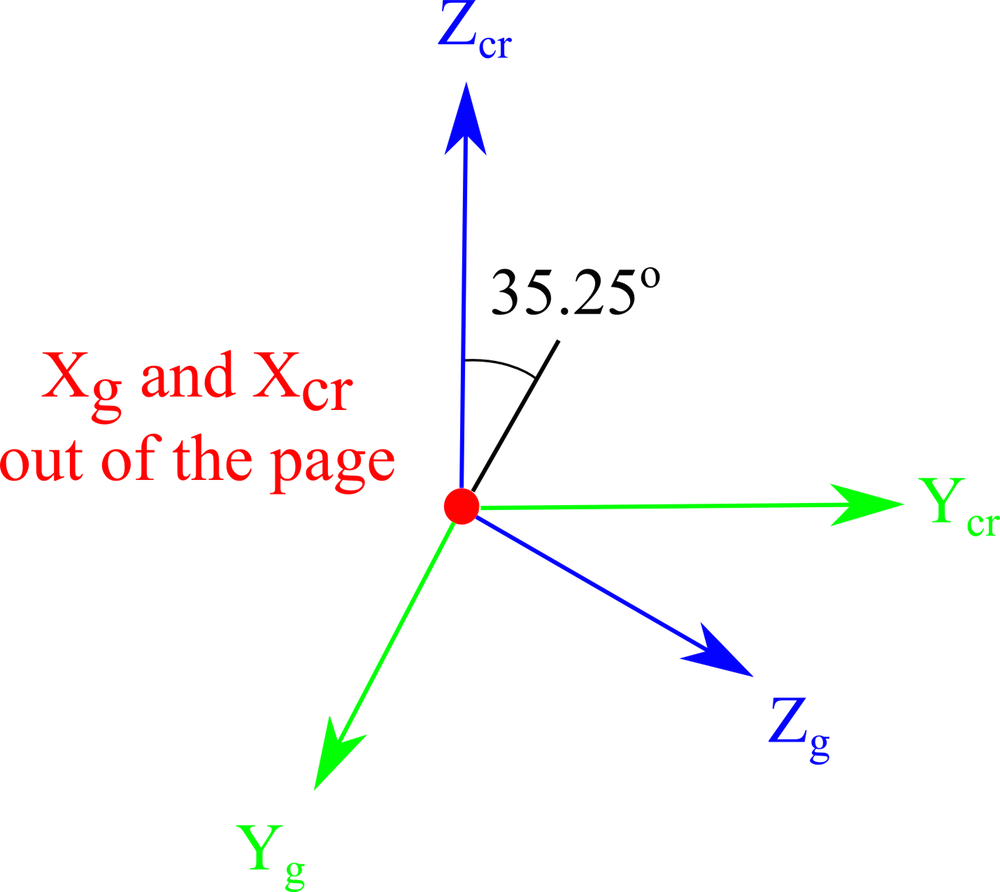 |
| 3. 将切割绕 w-(Yg)轴旋转 180°。 |  |
| 4. 重新调整上图的方向,使全局轴处于常见的指向。 | 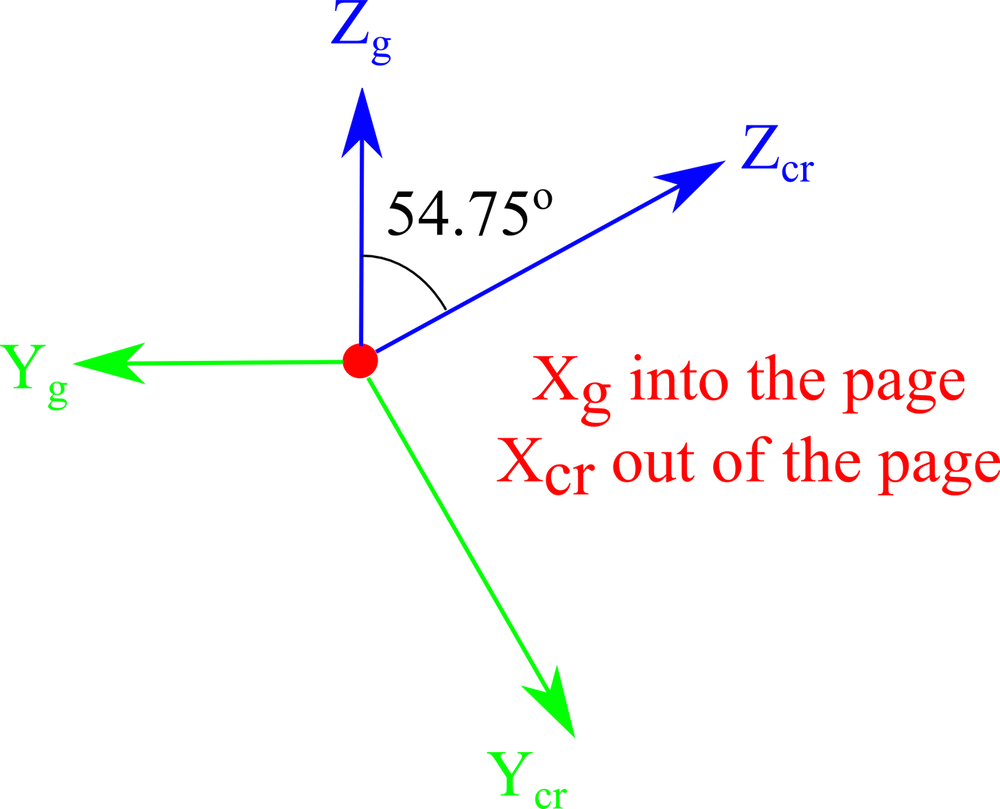 |
对应于 IEEE 1978 标准中的切割 (YXlw)-35.25° 180° 的旋转序列。
| 等效 Z-X-Z Euler 角 | |
|---|---|
| 1. 首先将晶体和全局轴对齐。 | 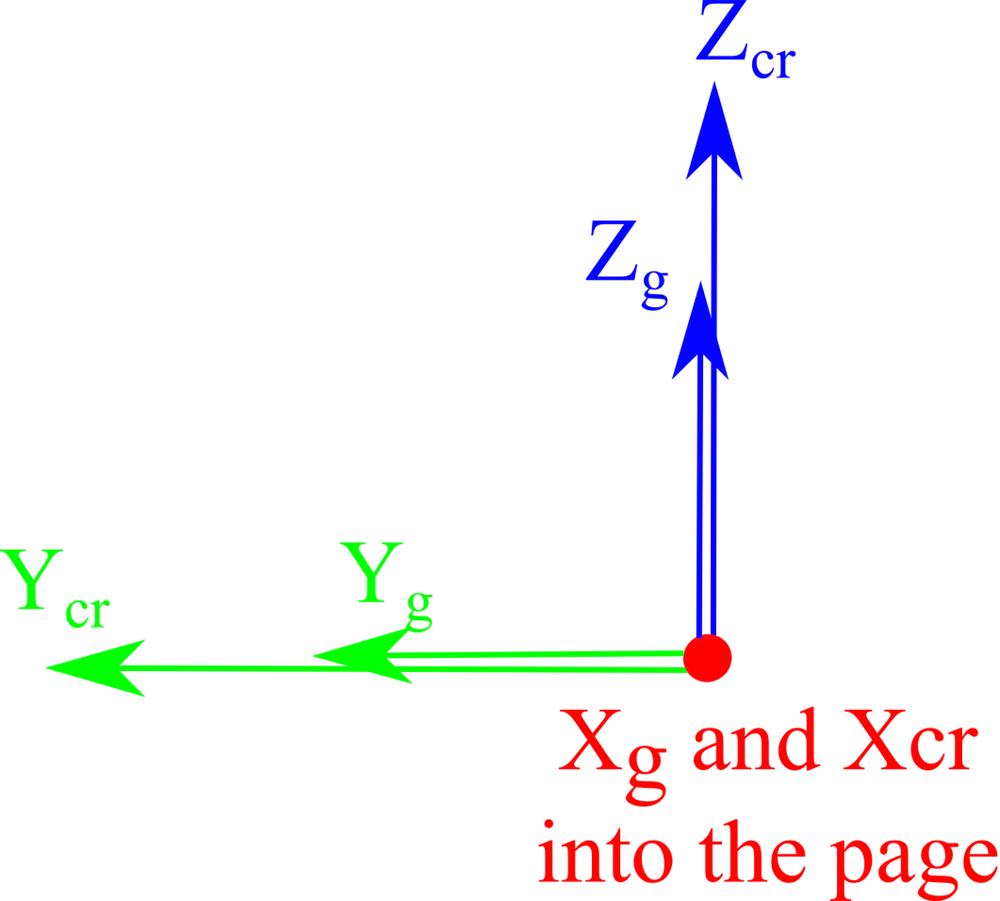 |
| 2. 将晶体轴绕 z 轴(Zcr)旋转180°。 |  |
| 3. 绕新的晶体 x 轴(Xcr)旋转晶体轴 -54.75°。 | 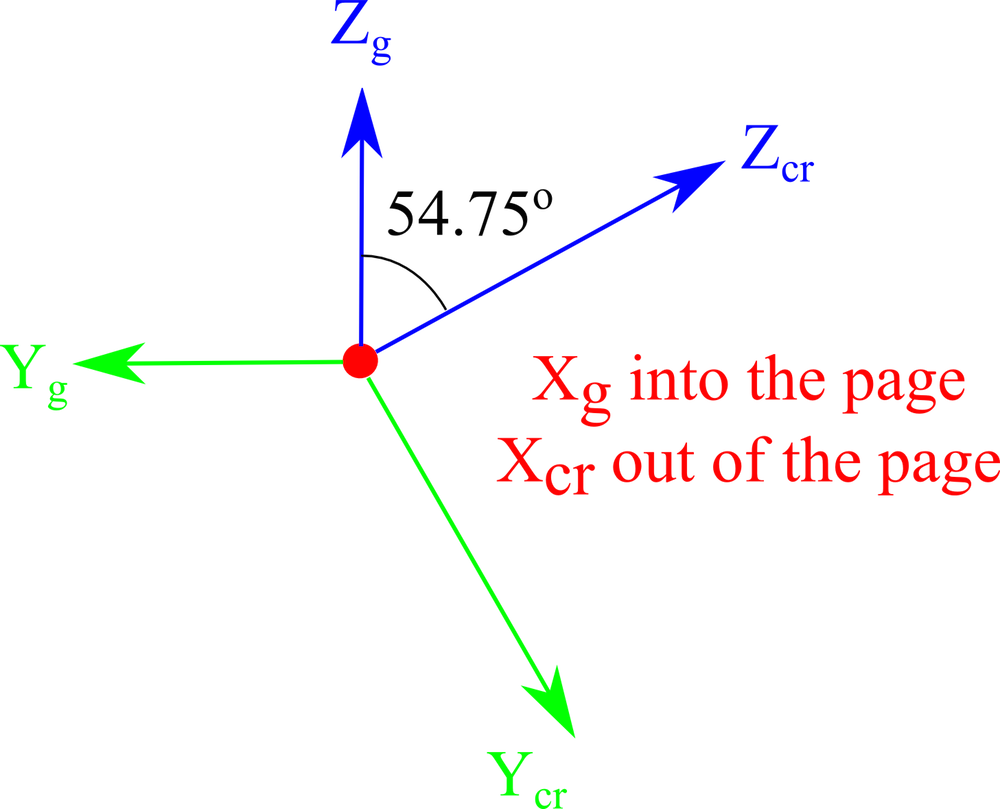 |
确定晶体轴相对于全局轴的 Euler 角的相应旋转。
| X | Z | X | |
|---|---|---|---|
| IEEE 1978 标准: (YXlw) -35.25° 180° | 180° | -54.75° | 0° |
IEEE 1978 标准中切割 (YXlw)-35.25° 180° 的 Euler 角。该切割与 IRE 1949 标准 AT 切割定义中板的方向完全相同。
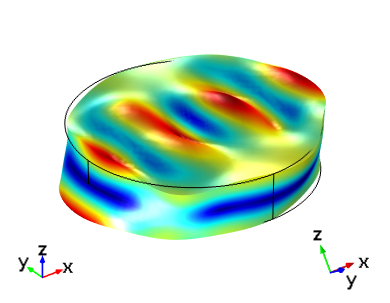
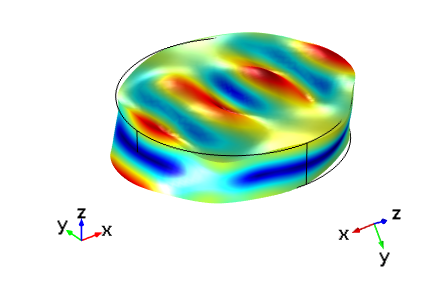
最后,下图显示了 IRE 1949 标准 AT 切与切割 (YXlw)-35.25° 180° 的频域响应的对比。不出所料,这两个设备的响应现在是相同的。
| IRE 1949 标准: (YXl) 35.25° | IEEE 1978 标准: (YXlw) -35.25° 180° |
|---|---|
 |  |
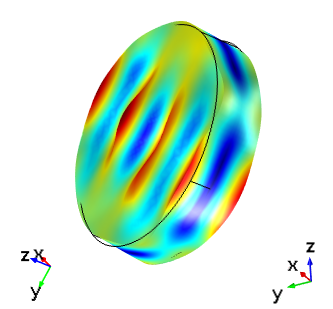 | 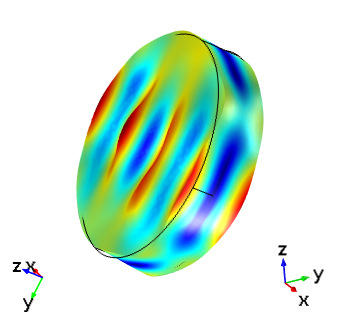 |
在驱动频率为 5.095 MHz 下,IEEE 1978 标准中的切割 (YXlw) -35.25 180 与根据 IRE 1949 标准设置的 AT 切晶体的厚度剪切模式对比。在每个图像中,左侧显示了全局轴方向,右侧显示了晶轴方向。顶部图像与全局坐标对齐,底部图像显示的晶体坐标与本文第一幅图中的方向相同。
拓展阅读
- 下载文中的教程:厚度剪切模式石英振荡器
- 阅读相关博客文章:压电材料:标准简介
对于工程师而言,标准既是我们工作中不可分割的一部分,也是我们之间用以交流复杂信息的通用语言。但标准委员会并非万能,有时一些修订标准也没能被广泛接受。压电材料的相关标准就碰到了类似问题,尤其是在石英晶体中。本篇博客将介绍目前关于压电材料的两套不同标准,虽然我们的侧重点是石英,但其中所述标准同样适用于所有压电材料。
压电材料
受到压力作用时,压电材料就会出现电极化。从微观角度来说,当实体变形时,带电原子在晶胞内的位移会在介质中产生一个净电偶极矩。在一些晶体结构中,这会造成一些宏观的平均偶极矩以及对应的净电极化。这就是正压电效应,,一般会伴有逆压电效应,即压电材料因置于电场中而产生机械形变。
要描述某类材料的压电效应,我们必须首先定义几种材料属性。材料极化与变形之间的关系可以通过以下两个方面进行定义:应变-电荷型或应力-电荷型。每个方程形式中的材料属性设定不同。
更麻烦的是,现在其实有两套不同的书面标准:IEEE 1978标准 和 IRE 1949标准,两套标准中材料属性的形式也有差异。IEEE 在 1987 年对 IEEE 1978 标准进行过修订,但因修订中包含一些错误,所以本次修订随即被取消。对此感到很困惑吗?我承认当我第一次阅读标准协议时,感觉就是如此。
本篇博客将详细介绍两套标准中不同的方程形式和标准,同时将侧重于石英晶体,这一带给我们最多困扰的材料。在学术界和工业界,较早的1949 IRE标准中对石英材料属性的定义较为常用,但其他材料的属性大多定义于1978 IEEE标准。更麻烦的是,在定义某些材料属性时,业界并没有表明他们所参照标准的习惯。
两种方程形式:应变-电荷型和应力-电荷型
至于结构域和电气域之间的耦合,可以表示为材料应力与在恒定应力下介电常数之间的联系,或是材料应变与在恒定应变下介电常数之间的耦合。以下为这两种方程形式:
应变-电荷型
应变-电荷型可以写为:
\bf{S}=s_E \bf{T}+d^T \bf{E} \\[3mm]
\bf{D}=d \bf{T}+\epsilon_0 \epsilon_{rT} \bf{E}
\end{array}
其中 S 代表应变,T 代表应力,E 代表电场,D 代表电位移场。材料参数 sE, d 和 εrT 分别代表材料的柔度、耦合属性和在恒定应力下的相对介电常数。ε0 为真空介电常数。这些物理量为分别为 4 阶、3 阶和 2 阶的张量。但由于物理原因,这些张量高度对称。它们同样可以用带缩略下标的矩阵单元表达,这更为简便。在协议中,Voigt 符号更为常用。
如果使用此符号体系,上述两个方程式则可以写为:
\left(
\begin{array}{l}
S_{xx} \\
S_{yy} \\
S_{zz} \\
S_{yz} \\
S_{xz} \\
S_{xy} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}
s_{E11} & s_{E12} &s_{E13} &s_{E14} &s_{E15} &s_{E16}\\
s_{E21} & s_{E22} &s_{E23} &s_{E24} &s_{E25} &s_{E26}\\
s_{E31} & s_{E32} &s_{E33} &s_{E34} &s_{E35} &s_{E36}\\
s_{E41} & s_{E42} &s_{E43} &s_{E44} &s_{E45} &s_{E46}\\
s_{E51} & s_{E52} &s_{E53} &s_{E54} &s_{E55} &s_{E56}\\
s_{E61} & s_{E62} &s_{E63} &s_{E64} &s_{E65} &s_{E66}\\
\end{array}
\right)
\left(
\begin{array}{l}
T_{xx} \\
T_{yy} \\
T_{zz} \\
T_{yz} \\
T_{xz} \\
T_{xy} \\
\end{array}
\right)
+
\left(
\begin{array}{lll}
d_{11} & d_{21} & d_{31} \\
d_{12} & d_{22} & d_{32} \\
d_{13} & d_{23} & d_{33} \\
d_{14} & d_{24} & d_{34} \\
d_{15} & d_{25} & d_{35} \\
d_{16} & d_{26} & d_{36} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\left(
\begin{array}{l}
D_{x} \\
D_{y} \\
D_{z} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}
d_{11} & d_{12} &d_{13} & d_{14} & d_{15} & d_{16}\\
d_{21} & d_{22} &d_{23} & d_{24} & d_{25} & d_{26}\\
d_{31} & d_{32} &d_{33} & d_{34} & d_{35} & d_{36}\\
\end{array}
\right)\left(
\begin{array}{l}
T_{xx} \\
T_{yy} \\
T_{zz} \\
T_{yz} \\
T_{xz} \\
T_{xy} \\
\end{array}
\right)
+
\epsilon_0 \left(
\begin{array}{lll}
\epsilon_{rT11} & \epsilon_{rT12} & \epsilon_{rT13} \\
\epsilon_{rT21} & \epsilon_{rT22} & \epsilon_{rT23} \\
\epsilon_{rT31} & \epsilon_{rT32} & \epsilon_{rT33} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\end{array}
应力-电荷型
应力-电荷型方程形式为:
\bf{T}=c_E \bf{S}-e^T \bf{E} \\[3mm]
\bf{D}=e \bf{S}+\epsilon_0 \epsilon_{rS} \bf{E}
\end{array}
材料参数 cE、e 和 εrS 分别代表了材料的刚度、耦合属性和在恒定应变下的相对介电常数。ε0 为真空介电常数。同样,这些物理量分别为 4 阶、3 阶和 2 阶的张量,也可以通过缩略下标的方式表达。
使用 Voigt 符号,则这些部分可被写为:
\left(
\begin{array}{l}
T_{xx} \\
T_{yy} \\
T_{zz} \\
T_{yz} \\
T_{xz} \\
T_{xy} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}
c_{E11} & c_{E12} &c_{E13} &c_{E14} &c_{E15} &c_{E16}\\
c_{E21} & c_{E22} &c_{E23} &c_{E24} &c_{E25} &c_{E26}\\
c_{E31} & c_{E32} &c_{E33} &c_{E34} &c_{E35} &c_{E36}\\
c_{E41} & c_{E42} &c_{E43} &c_{E44} &c_{E45} &c_{E46}\\
c_{E51} & c_{E52} &c_{E53} &c_{E54} &c_{E55} &c_{E56}\\
c_{E61} & c_{E62} &c_{E63} &c_{E64} &c_{E65} &c_{E66}\\
\end{array}
\right)
\left(
\begin{array}{l}
S_{xx} \\
S_{yy} \\
S_{zz} \\
S_{yz} \\
S_{xz} \\
S_{xy} \\
\end{array}
\right)
+
\left(
\begin{array}{lll}
e_{11} & e_{21} & e_{31} \\
e_{12} & e_{22} & e_{32} \\
e_{13} & e_{23} & e_{33} \\
e_{14} & e_{24} & e_{34} \\
e_{15} & e_{25} & e_{35} \\
e_{16} & e_{26} & e_{36} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\left(
\begin{array}{l}
D_{x} \\
D_{y} \\
D_{z} \\
\end{array}
\right)
=
\left(
\begin{array}{llllll}
e_{11} & e_{12} &e_{13} & e_{14} & e_{15} & e_{16}\\
e_{21} & e_{22} &e_{23} & e_{24} & e_{25} & e_{26}\\
e_{31} & e_{32} &e_{33} & e_{34} & e_{35} & e_{36}\\
\end{array}
\right)
\left(
\begin{array}{l}
S_{xx} \\
S_{yy} \\
S_{zz} \\
S_{yz} \\
S_{xz} \\
S_{xy} \\
\end{array}
\right)
+
\epsilon_0 \left(
\begin{array}{lll}
\epsilon_{rS11} & \epsilon_{rS12} & \epsilon_{rS13} \\
\epsilon_{rS21} & \epsilon_{rS22} & \epsilon_{rS23} \\
\epsilon_{rS31} & \epsilon_{rS32} & \epsilon_{rS33} \\
\end{array}
\right)
\left(
\begin{array}{l}
E_{x} \\
E_{y} \\
E_{z} \\
\end{array}
\right)
\\
\end{array}
上述方程中所定义的矩阵是对压电材料关键材料属性的定义。对于许多材料而言,由于晶体对称性,每个矩阵中都有一些单元为 0,而其他一些则可能相关。
使用国际符号来描述晶体对称性,石英晶体的对称群为 Trigonal 32。在不同标准中,非零矩阵单元的取值不同,这会给仿真中材料属性的指定造成困扰,尤其是对于石英而言,因为目前的两套标准都较常用。
最后,石英晶体中的另一个麻烦之处:石英晶体中不存在与纵轴相平行的对称面。因此,石英晶体的分类方法为:左或右对映,即左右对映现象(enantiomorphism)。 在左右对映形中,材料属性矩阵中特定单元的正负号会不同。
适用于石英及其他 Trigonal 32 材料的材料属性矩阵如下所示:请注意矩阵单元间的对称关系与我们所用的标准无关,也与该物质是左对映还是右对映无关。
\left(
\begin{array}{cccccc}
c_{E11} & c_{E12} &c_{E13} & c_{E14} & 0 & 0\\
c_{E12} & c_{E11} &c_{E13} & -c_{E14} &0 & 0\\
c_{E13} & c_{E13} &c_{E33} & 0 & 0 & 0\\
c_{E14} & -c_{E14} & 0 & c_{E44} & 0 & 0 \\
0 & 0 & 0 & 0 & c_{E44} & c_{E14}\\
0 & 0 & 0 & 0 & c_{E14} & \frac{1}{2}\left(c_{E11}-c_{E12}\right)\\
\end{array}
\right)
&
\left(
\begin{array}{cccccc}
s_{E11} & s_{E12} &s_{E13} & s_{E14} & 0 & 0\\
s_{E12} & s_{E11} &s_{E13} & -s_{E14} &0 & 0\\
s_{E13} & s_{E13} &s_{E33} & 0 & 0 & 0\\
s_{E14} & -s_{E14} & 0 & s_{E44} & 0 & 0 \\
0 & 0 & 0 & 0 & s_{E44} & 2 s_{E14}\\
0 & 0 & 0 & 0 & 2 s_{E14} & 2\left(s_{E11}-s_{E12}\right)\\
\end{array}
\right)
\\
\left(
\begin{array}{cccccc}
e_{11} &-e_{11} & 0 & e_{14} & 0 & 0 \\
0 & 0 & 0 & 0 & -e_{14} & -e_{11}\\
0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}
\right)
&
\left( \begin{array}{cccccc}
d_{11} & -d_{11} & 0 & d_{14} & 0 & 0 \\
0 & 0 & 0 & 0 & -d_{14} & -2d_{11} \\
0 & 0 & 0 & 0 & 0 & 0\\
\end{array}
\right)
\\
\left(
\begin{array}{ccc}
\epsilon_{rS11} & 0 & 0 \\
0 & \epsilon_{rS11} & 0 \\
0 & 0 & \epsilon_{rS33} \\
\end{array}
\right)
&
\left(
\begin{array}{ccc} \epsilon_{rT11} & 0 & 0 \\
0 & \epsilon_{rT11} & 0 \\
0 & 0 & \epsilon_{rT33} \\
\end{array}
\right)
\\
\end{array}
两套标准:1949 IRE 和 1978 IEEE
在 xyz 坐标系中,通过矩阵定义了不同应力或应变分量下的材料属性后,剩下的工作便是为后续写下材料属性定义一套一致的坐标系。
同样,所有标准都为相关晶类定义了一套一致的坐标系。但对于石英而言,随后的各套标准并未使用相同的坐标系,而且最新标准的普及程度不高。因此,我们必须首先明确一组给定的材料属性究竟是按照哪套标准定义的。
两套相关标准为:两套相关标准为:
- IEEE 1978标准:
- 这是大多数文献中对除石英之外其他材料最常参考的标准。有时它也会被用来明确石英的材料属性,举个例子,B. A. Auld 所著的 Acoustic Fields and Waves in Solids 中用的就是这一标准。
- IRE 1949标准:
- 各类文献通常会采用此标准中对石英材料属性的定义。
晶体坐标系的取向可以根据原子在晶胞内的指向确定(但实际的可操作性不强),或者根据晶形指向确定。晶形是指一组对称的晶面。每一种矿物都有一定的晶形,因此晶形可用来鉴别矿物。
Quartz Page中介绍了许多常见的晶形,分别以 m、r、s、x、z 和 a 表示,并且还有专门的页面介绍对应晶形的 密勒指数,这非常有助于我们辨别各种晶形。各类标准通常会用晶形来进行坐标轴取向,下图即为 1978 和 1949 中所用的坐标轴。请注意图中同时有左对映和右对映石英的坐标轴图片。
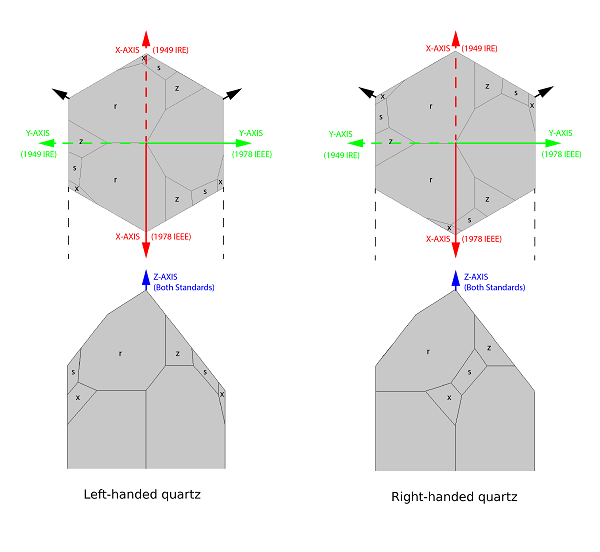
在 1978 IEEE(实线)和 1949 标准(虚线)中定义的晶轴 (点击图片放大)
由于不同晶体坐标轴的关系,当参考不同的标准时,左对映和右对映石英的材料属性的正负号会不同。下表总结了石英材料属性的正负号差异:
| IRE 1949 标准 | IEEE 1978 标准 | |||
|---|---|---|---|---|
| 材料属性 | 右对映石英 | 左对映石英 | 右对映石英 | 左对映石英 |
| sE14 | + | + | — | — |
| cE14 | – | — | + | + |
| d11 | — | + | + | — |
| d14 | — | + | — | + |
| e11 | — | + | + | — |
| e14 | + | — | + | — |
晶体切片的两个定义
通常情况下,石英类压电材料主要以薄晶片的形式使用,即按照相对于晶轴的特定角度切割的薄片。压电晶体切片的取向在 1948 及 1978 两套标准中都有定义。切片相对于晶体坐标系的指向是由一系列的旋转角度确定的,通常按照下图所示的格式表示:
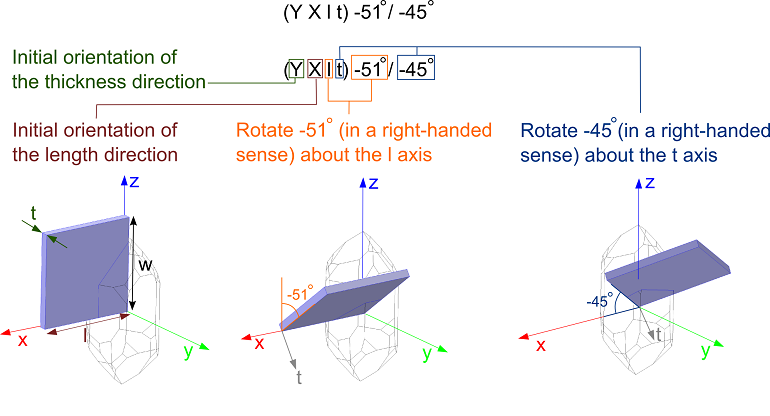
上图显示了石英 GT 切面在 1978 IEEE 标准中的定义,本晶体为右对映石英。
括号中的前两位表示从晶体上切下的压电片的厚度与长度方向。从左图中不难看出,厚度方向 (t) 与 Y 轴对齐,而长度方向 (l) 与 X 轴对齐。石英片还有第三个维度,那就是宽度 (w)。紧跟前两个字母的就是对切片边缘旋转角度的定义。
在上例中,第一个旋转角度是指 l 轴旋转 -51°。角度前面的负号表示切片将沿着坐标轴反向旋转、即向右旋转。另外一个旋转角度是指 t 轴将旋转 -45°。
在实际切割中,大多会定义一或两个旋转角度,但根据协议我们也可以定义第三个旋转角度,允许切片进行完全任意旋转。
请注意,因为 1949 标准和 1978 标准对晶轴的定义不同,所以两套协议中对晶体切面的定义也不同。AT 截法在石英片中较为常见,以上两套标准对此的定义是:
| Standard | AT Cut Definition |
|---|---|
| 1949 IRE | (YXl) 35.25° |
| 1978 IEEE | (YXl) -35.25° |
下图显示了两套标准中根据各自的坐标轴所定义的 AT 截法。
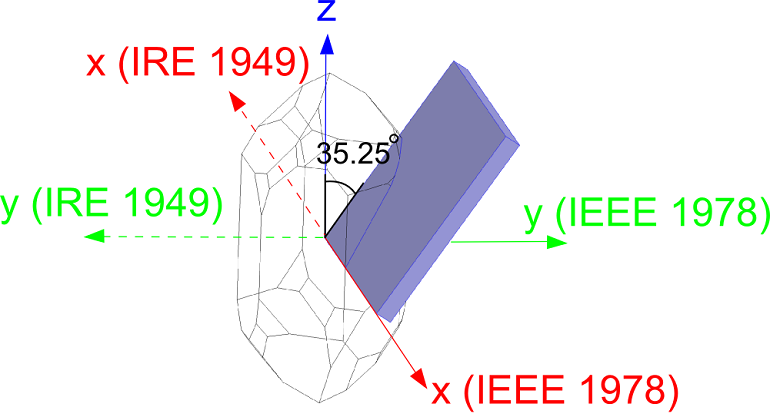
在 IRE 1949中,AT 截法定义为 (YXl) 35.25°,而 IEEE 1978 中则将其定义为 (YXl) -35.25°。上图显示了在右对映石英晶体中对切片的定义。这些标准间的差异是由于对晶轴取向的约定不同而造成的。在 IRE 1949 标准中,旋转角度为正,即如与X 轴对齐的话,则将 l 轴向右旋转。由于 IEEE 1978 标准中的规定不同,标准中所定义的旋转角度为负。
下一步
现在我们已经看出这两套不同的标准会如何影响我们对材料属性和晶体切面的定义。
在接下来的博客中,我们还将继续讲述如何根据这两套标准建立COMSOL Multiphysics模型。COMSOL Multiphysics中同时包含有两套标准中对材料属性的定义,因此您完全可以根据自己最熟悉的标准完成建模。请继续保持关注!