Temesgen Kindo – COMSOL 博客 -

非标准约束和弱贡献的力量

Tue, 16 Oct 2018 05:49:41 +0000

你有没有遇到过这种情况：你想为一个物理问题添加某个边界或域条件，但是找不到 COMSOL 软件中内置的功能？今天，我们将向您展示如何使用弱贡献特征来实现非标准约束。实际上，弱贡献是 COMSOL 软件内部用于施加内置域和边界条件的功能。它提供了一种灵活且不依赖物理场的方式，来扩展 COMSOL Multiphysics^® 软件的适用性。

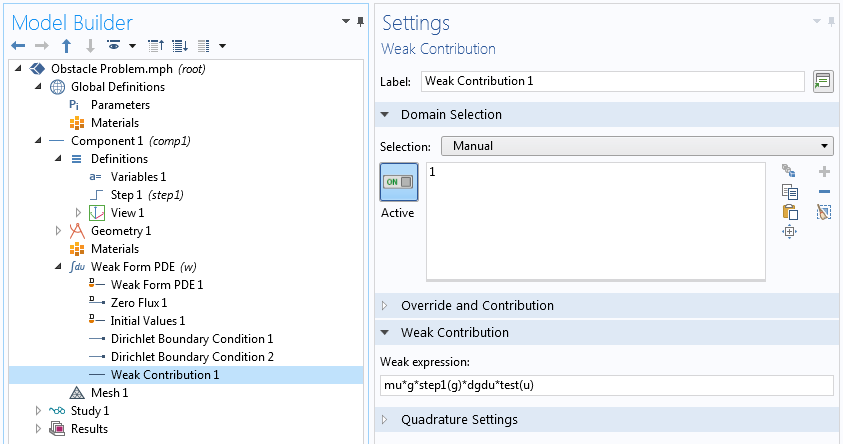
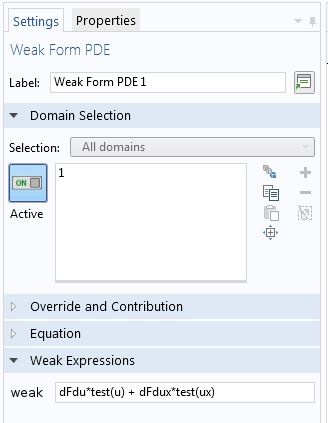
弱贡献简介

在 COMSOL Multiphysics 中解决的许多问题都可以看作是寻找能使某些量最小化的函数。例如，在弹性平衡问题中，我们要寻找的是使总应变能最小的位移。在关于变分问题和约束系列博客中，我们介绍了如何使用弱形式偏微分方程 接口来解决有约束和无约束的变分问题。我们使用了一个广义的约束框架来处理对解的各种限制。在该系列文章中，我们向您展示了如何实现无约束和有约束的问题。

通常，要最小化某个量是很好理解的，而在具体的问题中，我们要指定的是约束设置。理想情况下，我们不应该在无约束问题上浪费时间做无用功。通常，约束是边界条件，但有时它们可能是在每个点或通过解的积分来满足的要求。虽然 COMSOL Multiphysics 中内置了多个边界条件和其他约束选项，但您可能时不时的需要添加一两个新约束。今天，我们将介绍如何使用弱贡献实现这一点。

在这篇博文中，我们将：

快速回顾一下为变分问题添加约束的情况
使用弱贡献将非标准约束添加到一些著名的方程中
将这个数学思想与一些更具有物理实际意义的实现场景进行比较

为极值问题添加约束

在关于变分问题和约束的系列博客中，我们详细讨论了该主题的分析和数值模拟以及如何在 COMSOL^® 软件中实现。不熟悉该主题的读者可以先阅读该系列文章，获得一些理解。本节，我们从今天的示例中总结了所需的主要思想。

拉格朗日乘子法用于将约束的变分问题转变为等效的无约束问题。考虑约束变分问题

(1)

\textrm{找到函数} u(x) ,\textrm{ 取极小值 } E[u(x)] = \int_a^b F(x,u,u^{\prime})dx,

(2)

\textrm{ 对于任意 } x, \textrm{满足约束} g(x,u,u^{\prime})=0 .

该约束问题的可行临界点是增广泛函的驻点

(3)

E[u(x),\lambda(x)] = \int_a^b F(x,u,u^
{\prime})dx+\int_a^b\lambda(x)g(x,u,u^{\prime}
)dx.

取这个泛函的变分导数

(4)

\delta E = \delta \int_a^b F(x,u,u^

{\prime})dx+\delta \int_a^b\lambda(x)g(x,u,u^{\prime}
)dx.

假设问题不受约束的部分已经得到处理，我们只想添加必需的强制约束。那么我们的关注对象就只是上述方程中的第二项部分。在 COMSOL Multiphysics 中，当添加一个物理场接口时，可以将其视为添加无约束的变分问题。之后，可以通过一个或多个内置标准边界条件添加对边界和域的约束。如果我们有一个软件未内置的非标准约束怎么办？我们可以使用弱贡献灵活地添加此类条件。

回到上面的函数，让我们关注来自约束的贡献。

\delta E = \framebox

{其他项}+\delta \int_a^b\lambda(x)g(x,u,u^{\prime})dx = \framebox{其他项}
+ \int_a^b\left[\lambda \delta g+g\delta \lambda\right]dx .

对于上述的分布式约束，拉格朗日乘数是一个在受约束的几何实体上定义的函数。另一方面，对于全局约束，例如积分或平均约束之类，拉格朗日乘数是一个数字。假设我们要施加全局积分约束

\int_a^bg(x,u,u^

{\prime})dx-G = 0.

增广泛函是

E=\framebox{其他项} + \lambda\left[\int_a^bg(x,u,u’)dx – G\right]

它的变体是

\delta E=\framebox{其他项} + \lambda\int_a^b\delta g(x,u,u^{\prime}
)dx + \delta \lambda\left[\int_a^bg(x,u,u’)dx – G\right] ,

(5)

\delta E=\framebox

{其他项} + \lambda\int_a^b\left[\frac{\partial g}{\partial u}\delta u + \frac{\partial g}{\partial u’}\delta u’\right]dx + \delta \lambda\left[\int_a^bg(x,u,u’)dx – G\right].

因此，如果您想要对解强制执行的边界条件或其他约束不是内置的，但有一个内置的物理场接口，您需要做的就是使用 弱贡献 节点在上述方程中添加最后两项。下面，我们用一个例子来演示。

约束弹簧的平均垂直位移

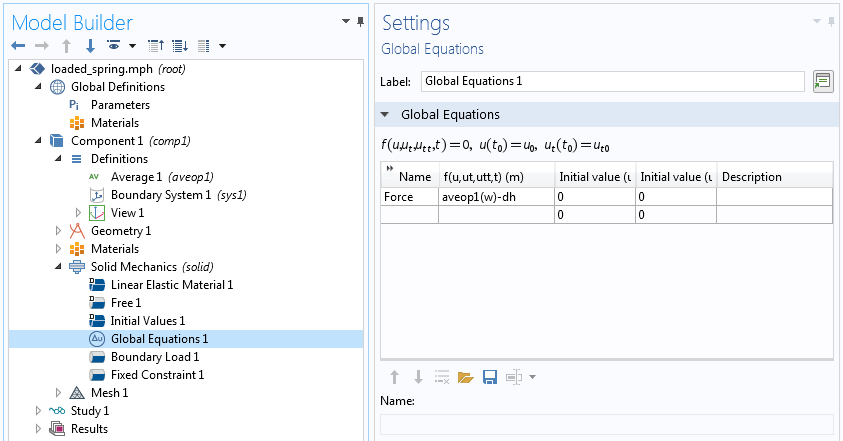
在这个示例中，一个弹簧被刚性固定在底端，我们希望顶端（下图中的边界 4）有 2 cm 的平均垂直位移。这是一个线性弹性问题，这个物理场是内置的。此外，刚性固定一个面是一个标准的边界条件。另一方面，没有指定面的平均位移。

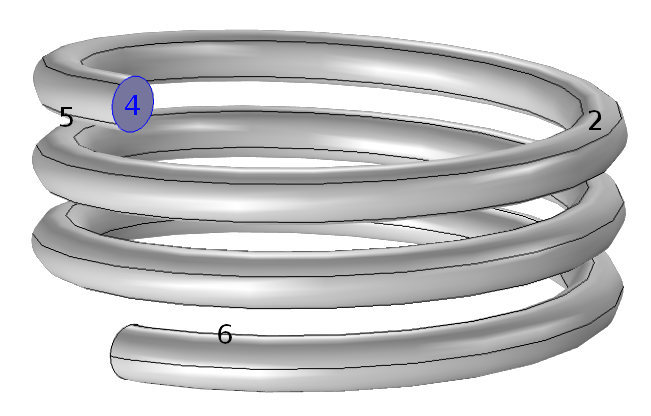
请注意，我们并不是要求面上每个点的垂直位移为 2 cm。这可以使用软件内置的指定位移 节点来指定。全局约束

(6)

\frac{\int_A wdA}{\int_A dA}-dh = 0,

其中，是有问题问题中的面，是所需的平均垂直位移（在我们的例子中为 2 cm）。这里，不是任何量的微分。它只是面上的平均垂直位移的参数名称。我们可以直接写为 2 cm。

除了使用标准特征实现这个约束之外，这个变分问题就变成了寻找增广泛函的驻点

\framebox{其他项}
+ \lambda\left[\frac{1}{A}\int_A wdA – dh\right].

对应的稳态条件是

(7)

\framebox{其他项} + \lambda\left[\frac{1} {A}\int_A \delta wdA\right] + \delta \lambda\left[\frac{1}{A}
\int_A wdA – dh\right] = 0, \quad \forall \quad \delta u, \delta v, \delta w, \delta \lambda.

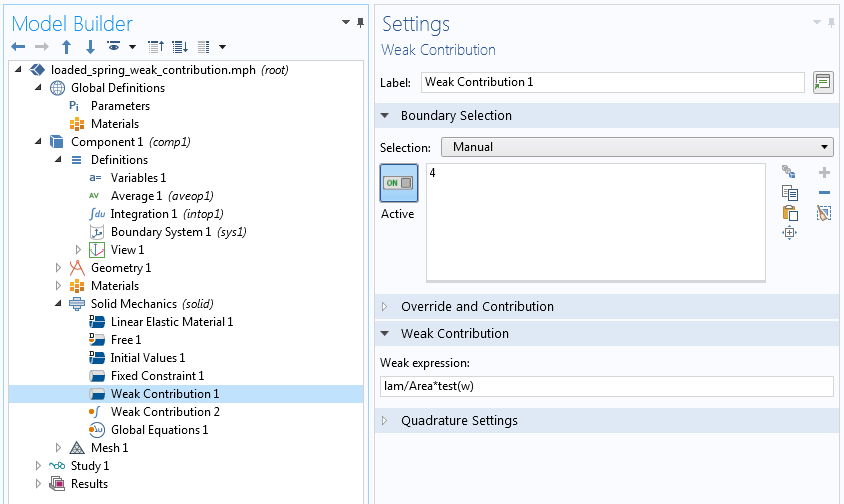
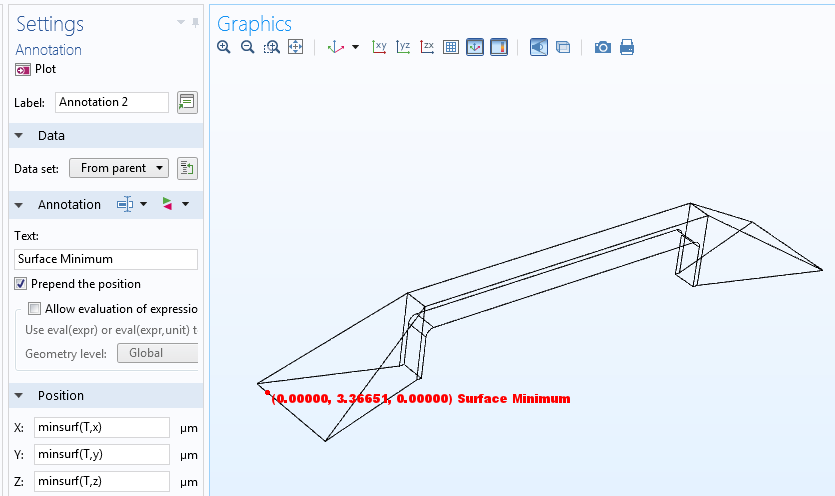
我们使用边界弱贡献和全局弱贡献来添加这两个贡献。在模型开发器中，我们可以通过图标区分边界和全局弱贡献。边界贡献与边界条件具有相同的图标，而全局贡献的图标有一个积分符号()。此外，边界贡献的设置窗口包含一个边界选择部分，而全局贡献没有几何实体选择。

对面上的平均位移施加约束边界和全局弱贡献。

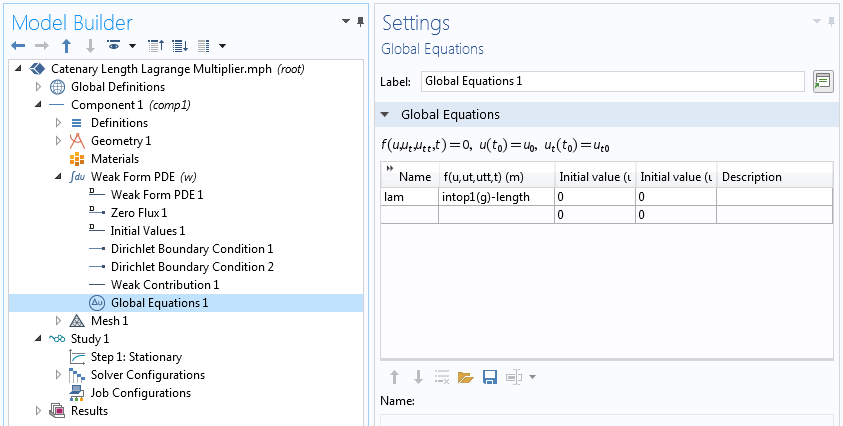
最后，变量是我们在拉格朗日乘法中定义的辅助全局变量。任何与约束相关的新变量都必须根据约束的性质在弱贡献节点的辅助变量 子节点或全局方程 节点中定义。

在我们的示例中，有一个全局约束，因此，我们必须使用全局方程 节点来定义它。通常，在全局方程 设置窗口中也会输入一个方程。这里没有必要，因为我们在弱贡献中包含了一个包含拉格朗日乘数变化的项。稍后将讨论另一种选择——使用全局方程 节点来定义全局自由度及其方程。全局方程为我们的问题增加了一个自由度。

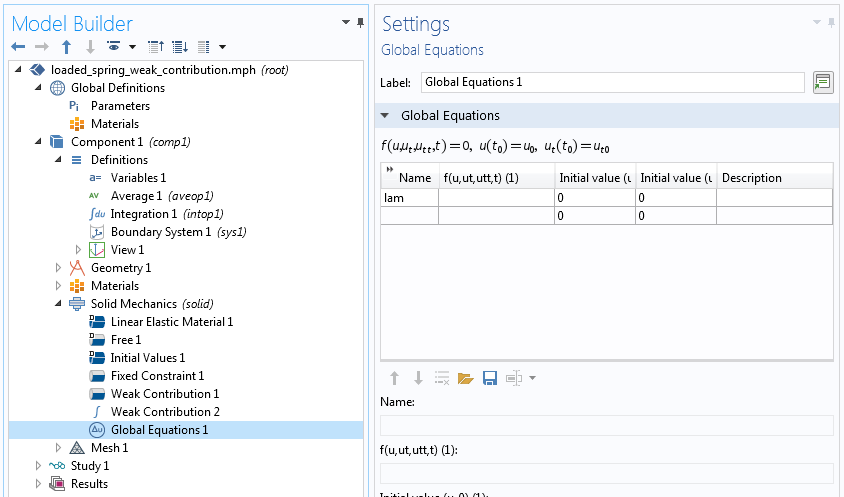
定义一个辅助全局未知数。

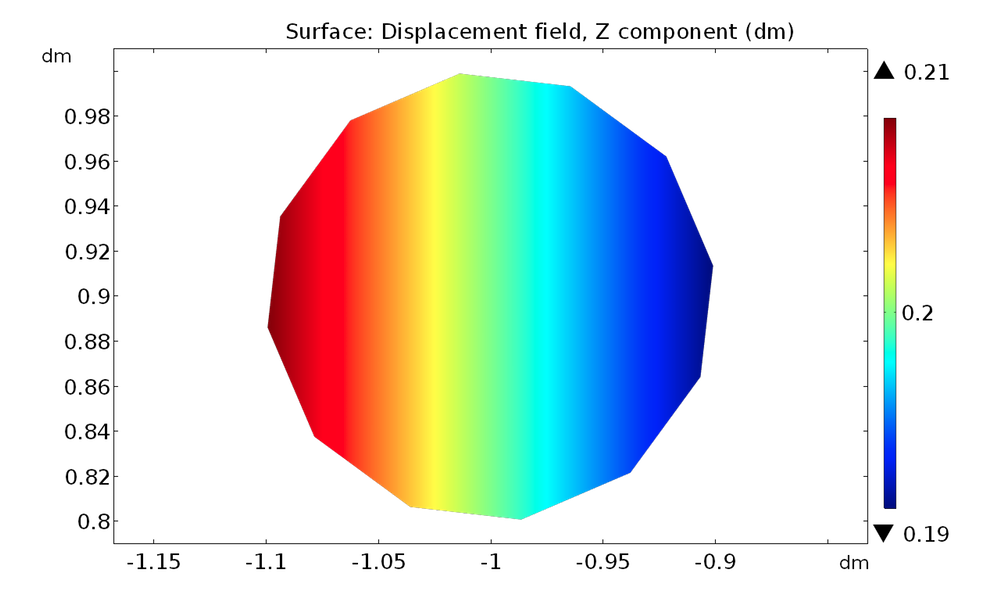
如果求解这个问题，我们会得到如下所示的解。我们可以在结果 > 派生值中看到拉格朗日乘数和平均位移。如果我们查看约束面上的垂直位移，可以发现它是不均匀的；它只是根据约束的要求平均为 2 cm。

关于上述实施的两个项目，我们想澄清两点：

(方程.7)中的第二项和第三项都包含积分。在边界弱贡献，弱贡献 1）中，我们只添加了被积函数。另一方面，全局弱贡献中的积分需要显式调用积分算子。或者，我们可以将被积函数 test(lam)*w/Area 添加到弱贡献1 并在弱贡献2 中仅保留 -test(lam)*dh。
这个示例中的约束是全局的。对于一个分布约束，拉格朗日乘数是一个位置函数，必须被定义为边界弱贡献下的辅助变量。有关这种区别的更多信息，请参阅我们关于变分约束的博客文章。

替代实现方法

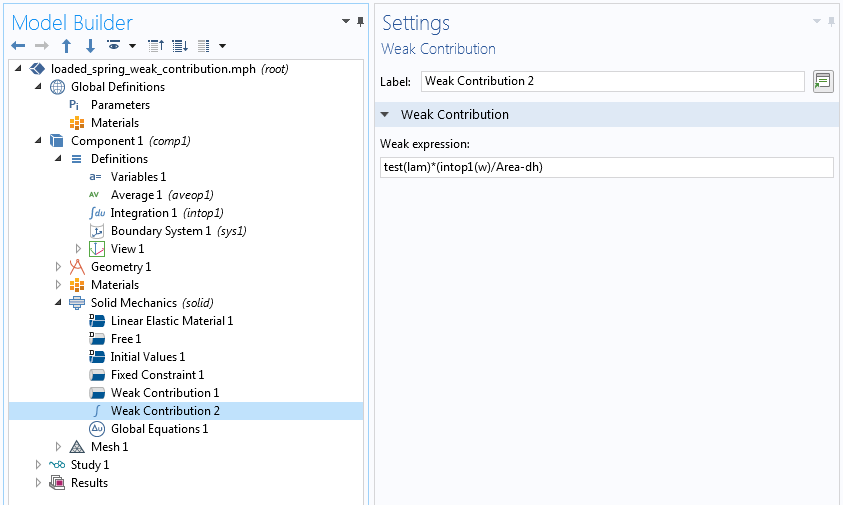
乘以拉格朗日乘数的变化项，可以在全局方程 节点中指定，该节点中定义了拉格朗日乘子。下面的屏幕截图显示了如何执行此操作。仅替换了（方程7）中的第三项。该项不包含，仍然必须指定为边界弱贡献。请注意，intop1() 是定义在边界 4 上的积分算子，Area 是由 intop1(1) 给出的边界的面积。

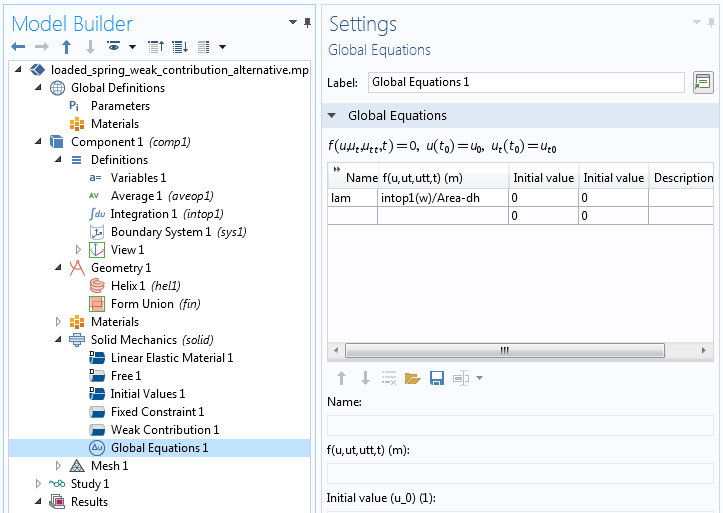
包含全局拉格朗日乘数变化的弱项的替代说明。

拉格朗日乘数的物理解释

上述解决方案为我们提供了由移动边界 4 引起的位移和应力，平均垂直位移 2 cm。问题是：我们如何在物理上强制结构符合我们的愿望？你猜对了。我们施加了一个力。拉格朗日乘数与强制执行约束所需的力（通量）有关。这里的关键词是相关的。接下来，让我们详细了解它的含义。首先，让我们尝试约束的另一种表达式。

(方程6) 中的约束在数学上等效于

(8)

\int_A wdA-Adh = 0.

对应于这种形式的约束的增广泛函是

\framebox

{其他项} + \lambda\left[\int_A wdA – Adh\right],

对应的稳态条件是

(9)

\framebox{其他项}
+ \lambda\left[\int_A \delta wdA\right] + \delta \lambda\left[\int_A wdA – Adh\right] = 0, \quad \forall \quad \delta u, \delta v, \delta w, \delta \lambda.

如果我们把这个方程中的最后两项作为弱贡献并求解，会得到一个拉格朗日乘数，这与我们在第一个操作中获得的结果大不相同。尽管如此，位移和应力仍是相同的。因此，我们可以怀疑，拉格朗日乘数本身并不是一个物理量，因此它不能告诉我们如何在物理上执行所需的约束。要找出我们应该在物理上做什么的一种可靠方法是，对结果进行后处理并查看反作用力(通量)。

为了严格确定拉格朗日乘数在物理上是什么，我们必须查看一下迄今为止一直隐藏的方程的无约束部分。在今天的这个例子中，就是查看固体力学方程的弱形式。对于处于平衡状态的可变形固体的弱形式，也称为虚功方程，由下式给出

(10)

-\int_V\sigma:\delta \varepsilon dV +\int_V\mathbf

{b}\cdot\delta\mathbf{u} dV+\int_A\mathbf{\Gamma}\cdot\delta\mathbf{u}dA =0 \quad \forall \delta\mathbf{u},

式中，是位移矢量和和分别是应力、应变、单位体积的体载荷和边界载荷。启用方程视图 可以查看任何 COMSOL Multiphysics 物理场接口的弱形式。

如果我们将(方程 10)、(方程 9) 和 (方程 7) 进行比较，会看到今天示例中的拉格朗日乘子与约束面上的边界载荷出现在同一位置。一个区别是拉格朗日乘数出现在表面积分外，而边界载荷在积分内部。这源于我们约束的全局性。另一个区别是我们示例中的拉格朗日乘数与垂直位移一起出现，而固体力学方程中的表面载荷是点乘以位移矢量的变化量。让我们逐一地来协调这些项目。

\int_A\mathbf{\Gamma}
\cdot\delta\mathbf{u}dA = \int_A\left[\Gamma_x\delta u + \Gamma_y\delta v + \Gamma_z\delta w\right]dA.

现在，我们看到拉格朗日乘数与边界载荷的垂直分量有关。最后，如果边界载荷是恒定的，有

\int_A\Gamma_z\delta wdA = \Gamma_z\int_A\delta wdA .

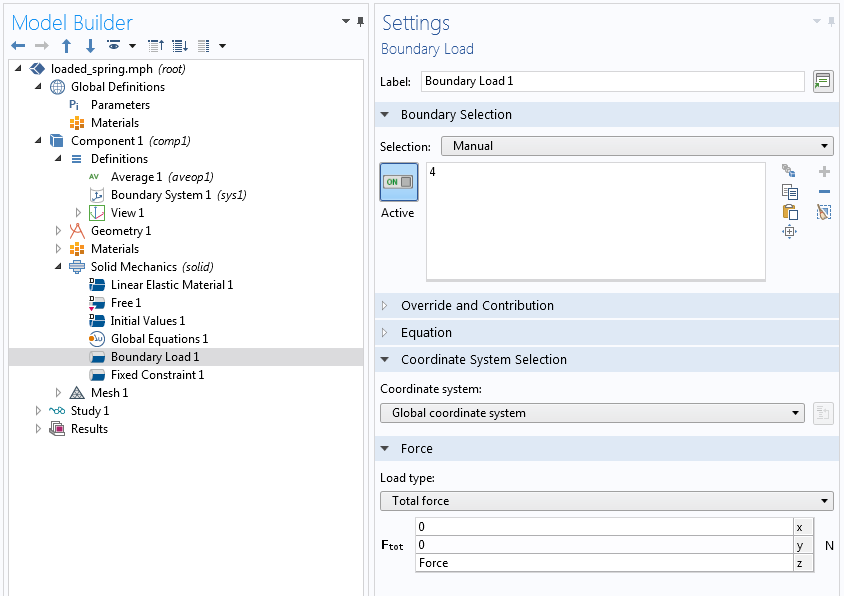
将其与（方程7）进行比较，可以看到在我们的第一个操作中，拉格朗日乘数对应于总垂直边界载荷。现在我们知道对于特定物理场和特定形式的约束方程，拉格朗日乘数是面上的总垂直载荷，我们可以使用内置的边界载荷 节点来强制约束而不是弱贡献。这一过程可以在 COMSOL 案例库中负载弹簧案例教程中详细查看。

当我们知道拉格朗日乘数的对应物理意义的替代实现方案。

最后一个实现可以看作是要求软件施加所需的任何垂直总力来强制平均垂直位移。我们可以这样做，是因为通过查看固体力学方程的弱形式，我们确定了拉格朗日乘数和总力之间的对应关系。我们并不总是可以用标准力（通量）项建立这种联系。请注意，我们可以使用默认的分布式边界载荷，这只会改变内部使用的额外自由度的数量。

一般来说，对于维度一致性，在(方程3)中，拉格朗日乘数与约束的乘积应该给出每单位体积、面积或长度“能量” 的密度，这取决于约束所应用的几何实体。在许多工程问题中，字面上代表能量，因此，我们说拉格朗日乘数与约束在能量上共轭。这意味着，例如如果我们缩放、平方或进行任何数学上改变约束方程单位的操作，那么拉格朗日乘数的单位和物理意义就会改变。然而，是不变的，因为它总是与(方程 5)能量共轭。拉格朗日乘数和雅可比约束的乘积在广义上是一个力（通量）密度。如果，这通常是线性约束的情况，拉格朗日乘数确实是广义力(通量)。

弱贡献的美妙之处在于，您可以强制执行约束，而无需通过内置物理场的弱形式。您可以对结果进行后处理以找出实际的物理过程。该实现与物理场无关。

关于弱贡献的总结性思考

今天，我们讨论了 COMSOL Multiphysics 软件如何帮助非标准边界条件的实施。使用弱贡献，我们可以用一个灵活的且与物理场无关的策略来添加不常用到成为软件标准功能的约束。该方法的数学本质是求解某个量的最小极值问题，但这种思想可用于由没有相应变分解的偏微分方程给出的问题。有关此主题的更多背景知识，我们推荐您阅读关于弱形式和变分问题的系列博客。

下一步

如果您对弱贡献或其他主题有任何疑问，或者想详细了解 COMSOL Multiphysics 的特性和功能如何满足您的建模需求，欢迎您与我们联系。

联系 COMSOL

查看以下 COMSOL 案例库中示例和博客文章，了解在各种物理领域中使用弱贡献和额外方程的更多演示：

]]>

图像去噪以及其他多维变分问题

Fri, 21 Sep 2018 01:39:45 +0000

我们之前讨论了如何用 COMSOL Multiphysics 软件解决一维变分问题，并使用统一的强制约束（第3部分: 强制约束中数值问题的处理方法）框架实现复杂的域和边界条件。今天，我们使用了一个有意思的例子：变分图像去噪，将问题的讨论扩展到多维度、高阶导数和多个未知数。文章最后，我们对这个变分问题相关的系列博客进行总结，并对进一步的研究提出了一些建议。

高维空间中的变分问题

（之前的讨论中）考虑的是一维问题，并寻找一个函数使函数最小化

E[u(x)] = \int_a^b F(x,u,u^{\prime})dx.

现在，让我们考虑更高维的空间，同时只考虑一阶导数。考虑使下式最小化的变分问题

E[u(x,y,z)] = \int_{\Omega}F(x,y,z,u,u_x,u_y,u_z)d\Omega,

定义在固定域上

相邻函数就变成

E[u+\epsilon\hat{u}] = \int_{\Omega}
F\left(x,y,u+\epsilon\hat{u},\frac{\partial}{\partial x}(u+\epsilon\hat{u}
),\frac{\partial }{\partial y}(u+\epsilon\hat{u}),\frac{partial } {\partial z}(u+\epsilon\hat{u})\right)d\Omega.

与一维问题一样，一阶最优必要条件为

\frac{d}{d\epsilon}\bigg|_{\epsilon=0}E[u+\epsilon \hat u] = 0,

这意味着

\int_{\Omega} \left[\frac{\partial F}{\partial u}\hat{u}
+\frac{\partial F}{\partial u_x}\hat{u}_x+\frac{partial F} {\partial u_y}\hat{u}_y+\frac{\partial F}{\partial u_z}\hat{u}_z\right]d\Omega = 0, \quad \forall \quad \hat{u}(x,y,z).

为了得到变分导数，我们构建了一个函数，其本质是标量参数的函数并使用单变量演算方法。对于固定域，一种更快的正式方法是用变分导数符号表示为：

\delta E = \int_{\Omega} \delta Fd\Omega=\int_{\Omega} \left[\frac{\partial F}{\partial u}\delta u + \frac{\partial F}{\partial u_x}\delta u_x + \frac{\partial F}{\partial u_y}\delta u_y + \frac{\partial F}{\partial u_z}\delta u_z\right]d\Omega

这里，对应于之前使用的符号。注意，由于域是固定的，因此我们仅考虑函数及其导数的变化。如果域可以随解而变化，那么变分导数将包含来自边界变化的额外贡献。

图像去噪：一个多维变分问题

近几十年来，变分方法为图像处理带来了强大而严谨的技术，例如去噪、去模糊、修复和分割。今天，我们就以降噪为例来说明。总变分最小化 是一种用于图像去噪的技术。假设我们有一个图像数据，已被噪声破坏。图像上有斑点（有时称为“脉冲噪声”）。我们想要尽可能多的恢复原始图像，所以图像必须被去噪。

含细节错误的图像会包含高变分；因此，去噪后的图像应具有尽可能小的变分。经 Tikhonov 处理的模型将这个总变分测量为

TV(u) = \int_{\Omega}|\nabla u|^2d\Omega = \int_{\Omega}\nabla u \cdot \nabla ud\Omega.

仅将总变分最小化会尽可能地平滑数据并返回接近常数的解，从而丢失图像中的合理细节。为了防止出现这个问题，我们还希望将输入数据与解之间的差异最小化，由保真项给出

f(u)=\int_{\Omega}(u-u_o)^2d\Omega.

现在，我们有了多个可能相互冲突的目标，我们尝试通过引入新函数来折中

E(u) = \int_{\Omega}\left[ \nabla u \cdot \nabla u + \mu (u-u_o)^2\right]d\Omega

其中，正则化参数确定强调细节还是去噪（这是由用户指定的正数）。

如上一节所述，我们现在准备导出一阶最优条件。需要一个消失的变分导数，我们得到

\delta E = \int_{\Omega}\left[2 \nabla u \cdot \delta (\nabla u) + 2\mu (u-u_o)\delta u\right]d\Omega = 0 , \quad \forall \quad \delta u.

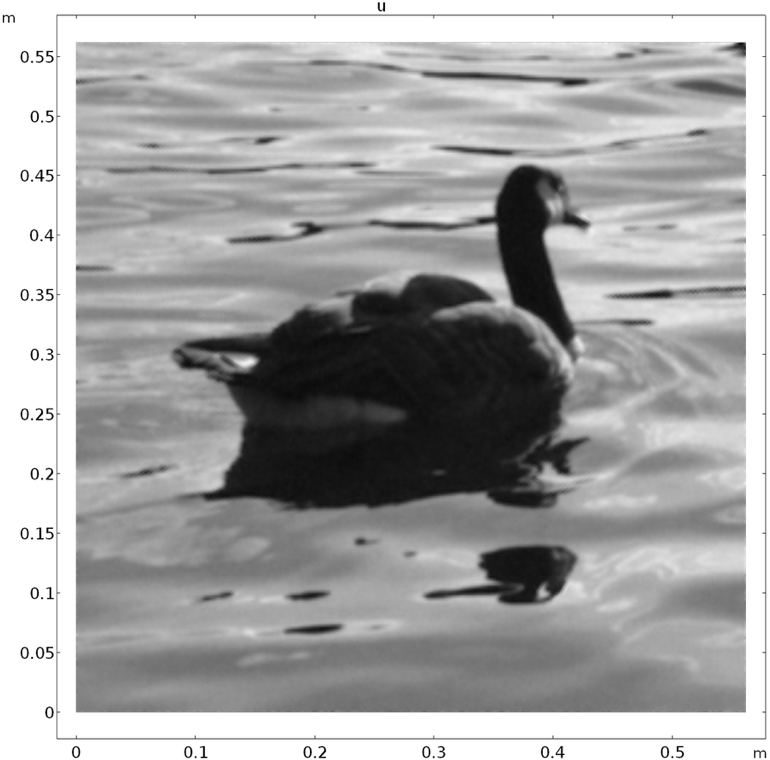
为了演示这个过程，我们将图像导入 COMSOL Multiphysics，并添加随机噪声来破坏它。以下是破坏了我同事提供的一只鹅的图像后得到的结果：

被随机噪声故意破坏的测试图像。

上面的弱形式以矢量表示法给出。为了在计算中使用，我们将其写为笛卡尔坐标表示，并忽略公因数 2。

\int_{\Omega}\left[u_x\hat{u}_x + u_y\hat{u}_y + \mu (u-u_o)\hat{u}\right]d\Omega = 0 , \quad \forall \quad \hat{u}.

将此公式输入到 COMSOL® 软件中，如下面的屏幕截图所示。通过在所有边界上使用 Dirichlet 边界条件，保留边上的数据，并使用正则化参数 1e6。在较简单的算法中，正则化参数是通过试错法确定的。如果生成的图像缺少相关细节，则我们增大参数；如果认为结果太嘈杂，我们就减小参数。

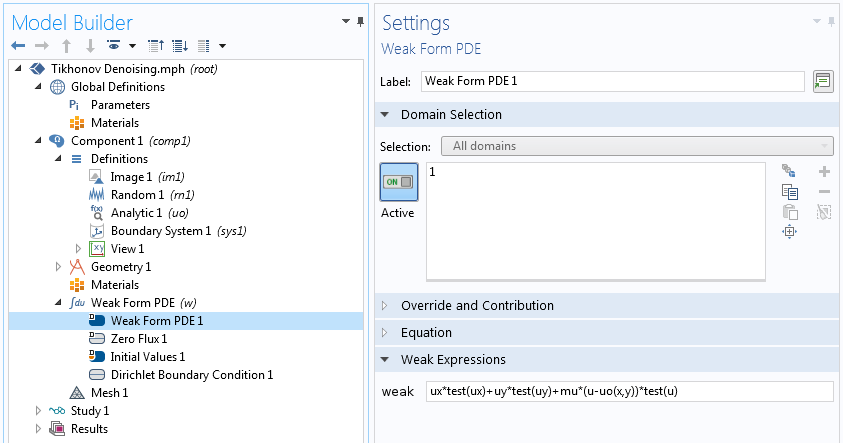
在二维中指定变分问题。

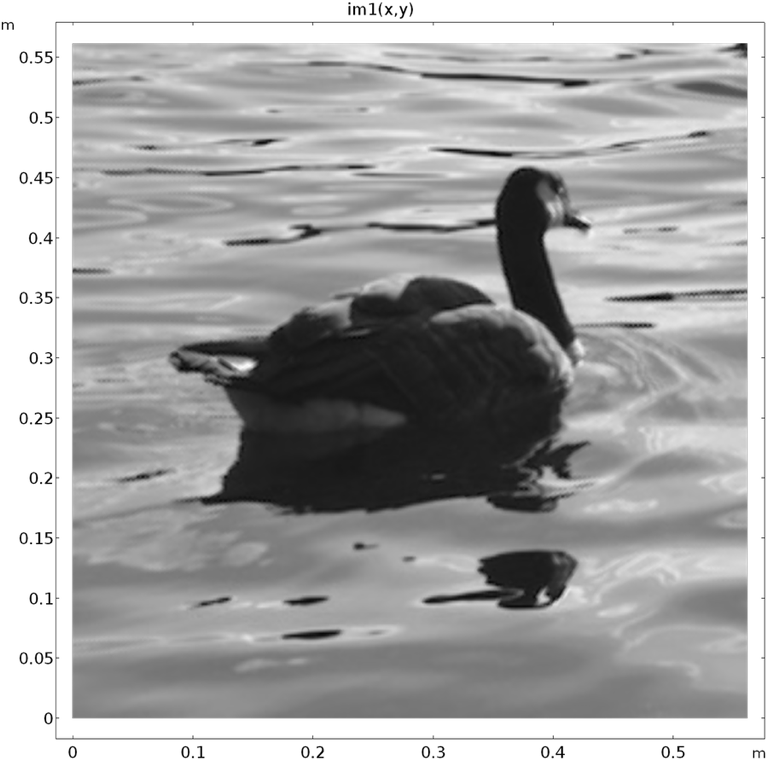
下面是去噪后的图像，以及原始图像——对于基本模型来说还不错！

去噪图像（左）和原始图像（右）。

Tikhonov 正则化会过于平滑，并且不会保留诸如边和角之类的几何特征。由下式给出的 ROF 模型的函数

E(u) = \int_{\Omega}\left[ |\nabla u| + \mu (u-u_o)^2\right]d\Omega

在这方面做得更好。

到目前为止，通过将变分导数设置为零而获得的最优性的一阶必要条件是

\delta E = \int_{\Omega}\left[ \frac{\nabla u}{|\nabla u|}\cdot \delta (\nabla u) + 2\mu (u-u_o)\delta u\right]d\Omega = 0 \quad \forall \delta u.

请注意，在函数中使用绝对值会导致高度非线性的问题。另外，分母可能在数值迭代中变为零，从而产生除零错误。为了防止这种情况，我们可以给它添加一个小正数。在 COMSOL Multiphysics 中，我们经常使用浮点相对精度 eps，大约是。

ROF 模型保留了边缘，但据说会引起所谓的“阶梯效应”。在函数中包含高阶导数有助于避免这种情况。

高阶导数的变分问题

下面，我们讨论高保真图像处理和其他涉及高阶导数的变分问题。这方面的一个传统课题是弹性梁和板的分析。例如，在欧拉梁理论中，一个具有杨氏模量 E 和截面惯性矩 I 的梁，施加横向载荷使其弯曲以最小化总势能

\int\left[\frac{1}{2}EI(\frac{d^2u}{dx^2})^2-fu\right]dx.

对于较小的变形，分析忽略了域的变化，因此可用类似于下式的变分公式求解

\delta \int\left[\frac{1}{2}EI(\frac{d^2u}{dx^2})^2-fu\right]dx = \int\left[EI\frac{d^2u}{dx^2}\delta(\frac{d^2u}{dx^2})-f\delta u\right]dx = 0 \quad \forall \delta u .

请注意，我们没有对变分导数中的杨氏模量求微分，因为我们考虑的是线性弹性材料，其中材料属性与变形无关。对于非线性材料，必须包括材料属性对变分导数的贡献。该功能内置于 COMSOL Multiphysics 的附加产品——非线性结构材料模块中。

在函数中包含高阶导数不会给我们发现一阶最优性准则的方法带来任何概念上的改变，但是它确实具有计算上的含义。有限元插值函数中在弱形式偏微分方程设置的离散化设置窗口 中，需要具有与变分形式中的最高阶空间导数相同或更高的多项式幂。例如，对于梁问题，存在变分形式的二阶导数，因此我们无法选择线性形状函数。如果我们这样做了，方程中的所有二阶导数都会一致消失。我们必须使用二次或更高阶的形状函数。

多未知数变分问题

到目前为止，我们已经考虑了最小化只基于一个未知数的函数。通常，函数包含不止一个未知数。假设我们还有另一个未知数和一个函数

E(u,v)=\int_{\Omega}F(x,y,z,u,v,u_x,u_y,u_z,\dotsc)d\Omega.

这个函数的第一个变分是

\delta E=\int_{\Omega}\left[\frac{partial F} {\partial u}
\delta u+\frac{\partial F}{\partial v}\delta v + \frac{partial F} {\partial u_x}\delta u_x+\frac{\partial F}{\partial u_y}\delta u_y+\frac{partial F} {\partial u_z}\delta u_z + \frac{\partial F}{\partial v_x}\delta v_x+\frac{partial F} {\partial v_y}\delta v_y+\frac{\partial F} {\partial v_z}\delta v_z+…\right]d\Omega.

这里，我们假设两个场和彼此独立，因此，我们可以对两个变量进行独立变分。有时，情况并非如此：变量之间可能存在约束。

变量之间最简单的约束是，当一个变量显式地以另一个变量的形式给出时，如。在这种情况下，我们对于以下函数，可以选择消除

E(u,v)=\int_{\Omega}F(x,y,z,u,v,u_x,u_y,u_z,\dotsc)d\Omega.

通常，我们有以下形式的约束，并且我们不能用代数的方法转换这个表达式。在这种情况下，我们使用系列博客第3部分中讨论的有关强制约束的技术。例如，对于拉格朗日乘数法，我们有一个由下式给出的增广函数

\mathcal{L}(u,v,\lambda) = \int_{\Omega}\left[F+\lambda g\right]d\Omega,

其中，为分布式约束，或

\mathcal{L}(u,v,\lambda) = \int_{\Omega}Fd\Omega\quad +\quad \lambda g,

其中，为全局约束的常数。

我们使用相同的 弱形式偏微分方程 接口来指定这类多场问题。问题是：我们是使用单个接口还是为每个未知函数都使用一个接口？这取决于未知函数之间的关系。一种情况，如果和是同一物理矢量的不同分量，例如位移或速度，我们可以使用相同的接口，并在因变量 部分指定因变量的数目。另一种情况，如果代表温度，代表电势，我们可以使用不同的偏微分方程接口。如果我们出于某种令人信服的原因，必须对同一未知向量的不同分量使用不同的离散化或缩放，我们也可以使用多个接口。当我们有多个未知数时，我们必须仔细选择每个场的插值函数（如之前博客文章中有关多物理场模型中单元阶次中介绍的那样。）

结束语

变分方法提供了一个统一的框架对大量科学问题进行建模。COMSOL Multiphysics 中包含的弱形式偏微分方程接口，使我们能够引入自己的变分问题来扩展 COMSOL^® 软件的功能。在这一系列博文中，我们通过解决一些问题来证明了这种功能，这些问题包括找到皂膜的形状，为湖边的徒步旅行者规划路线以及修复损坏的图像。

请记住，一些重要的偏微分方程并不是来自最小化泛函数。Navier-Stokes 方程是就是一个示例。我们仍可以在导出他们的弱形式后，使用弱形式偏微分方程 接口求解这类问题。

求解变分问题的一个重要部分是指定约束。本系列的前三篇博客文章讨论了强制约束的数学公式和数值分析。

这里需要注意的是，我们仅考虑了优化的必要条件。消除一阶导数不足以达到极小值。一阶导数在最大值上也消失了。在本系列讨论的示例中，我们考虑了众所周知的问题，在这些问题中通过解提供最小值。在处理新问题时，一定要在结束计算前检查二阶最优性准则以及最小值（最大值）的存在和唯一性。对于这个以及其他变分问题分析和数值方面的问题，我给大家提供一些我喜欢的参看文献，希望会对您有所帮助：

关于变分演算的经典文献：

I.M. Gelfand and S.V. Fomin (English translation by R.A. Silverman), Calculus of Variations, Dover Publications, Inc., 1963.

最近讨论工程问题的文章：

K.W. Cassel, Variational Methods with Applications in Science and Engineering, Cambridge University Press, 2013.
J.W. Brewer, Engineering Analysis in Applied Mechanics, Taylor & Francis, 2002.

强制约束的策略：

D.G. Luenberger, Introduction to Linear and Nonlinear Programming, Addison-Wesley Publishing Company, 1973.
S.S. Rao, Engineering Optimization: Theory and Practice, John Wiley & Sons Inc., 2009.

希望本系列文章使您对使用 COMSOL Multiphysics 模拟变分问题有所了解，尤其当你需要建模的问题还未在软件中内置时。

祝您建模愉快，如有任何疑问，请通过下面的按钮与我们联系：

联系 COMSOL

查看更多关于“变分问题和约束”的系列博客文章

]]>

实现不等式约束的方法

Mon, 17 Sep 2018 05:37:14 +0000

你知道怎样找到湖上两点之间最短的陆路距离吗?这种障碍物和解的边界通常被称为不等式约束。在接触力学中对物体间隙非负性的要求，在化学中对物种浓度的要求，以及在生态学中对种群的要求都是不平等约束的一些例子。在之前的系列博客中，我们讨论了变分问题中的等式约束。今天，我们将向您介绍如何在 COMSOL Multiphysics® 中基于方程建模时实现不等式约束。

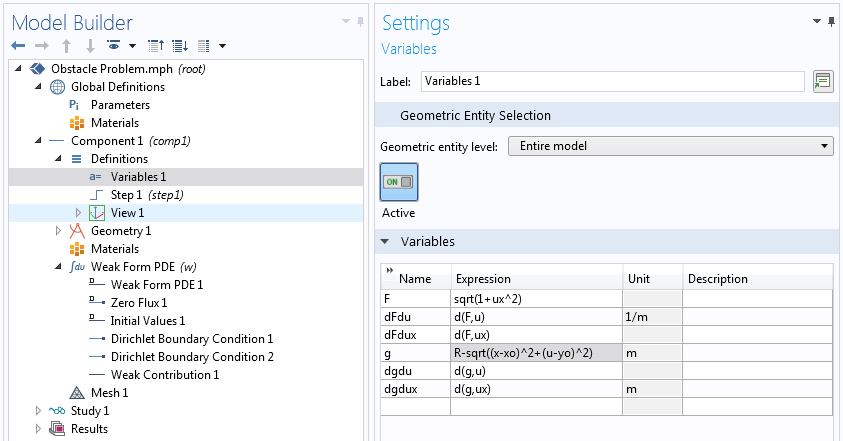
用于路径规划的罚函数法

假设你想从(0,0.2)点移动到(1,1)点，但是有一个圆心在(0.5,0.5)，半径为 0.2 的圆形障碍物。使两个端点和之间的距离最小的曲线应该使函数最小

E[x,u,u’] = \int_a^b \sqrt{1+u^{\prime}^2}dx.

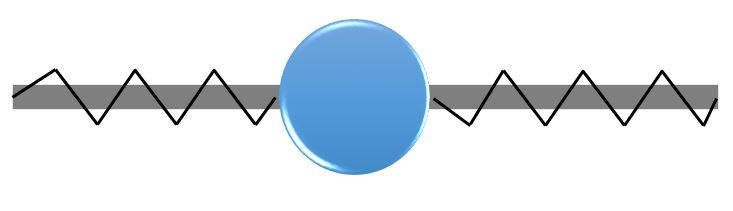
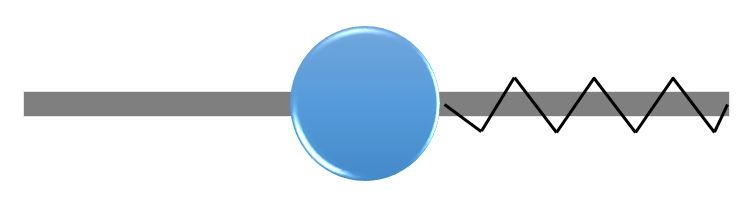
在欧几里得空间中，两点之间最短的距离是直线。因此，用我们已经讨论过的方法来解这个方程应该会得到一条直线。然而，在我们的例子中，这条直线穿过了障碍物。这是不可行的。我们必须遵循我们的路径不能进入障碍物的约束;即路径上某一点到圆形障碍物中心的距离应该大于或等于圆的半径。

R-\sqrt{(x-x_o)^2+(u(x)-y_o)^2} \le 0.

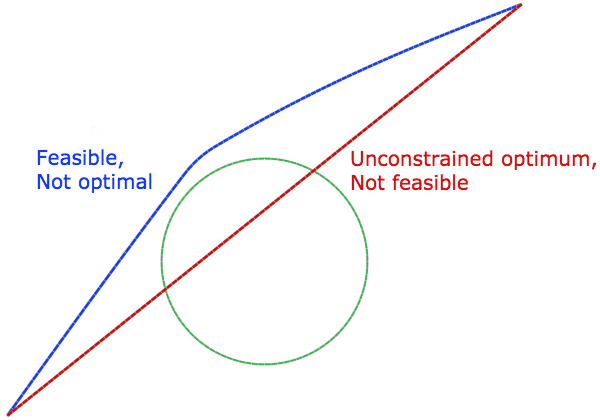
不等式约束问题的一个基本示意图。

我们要在函数中添加一个术语来惩罚约束违背。对于等式约束，我们惩罚的正负值。对于不等式约束，我们惩罚的正值，而接受负值。

在障碍物问题中，这意味着只有当路径试图穿过障碍时，我们才能进行惩罚。远离环形湖的海岸是可行的，虽然可能不是最优的，因此我们的惩罚正则化目标函数是

E_{\mu}[x,u,u’] = \int_a^b \sqrt{1+u^{\prime}
^2}dx + \frac{\mu}{2}\int_a^b\bigg\langle R-\sqrt{(x-x_o)^2+(u(x)-y_o)^2}\bigg\rangle^2dx,

其中，是惩罚参数，我们使用斜坡函数

\bigg\langle x \bigg\rangle:= \begin{cases}
x& x\ge 00 & x \le 0.\end{cases}

对于一般函数

E[x,u,u’] = \int_a^b F(x,u,u^{\prime}) dx

在不等式约束下被最小化

g(x,u,u^{\prime}) \leq 0, \qquad \forall x,

惩罚函数变成

E_{mu}[x,u,u’] = \int_a^b F(x,u,u^{\prime}) dx + \frac{\mu}{2}\int_a^b\bigg\langle g(x,u,u^{\prime})\bigg\rangle^2 dx.

最后一步是对上述函数求一阶变分导数，并将其设为零。这里，我们需要记住斜坡函数的导数是 Heaviside 阶跃函数。

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F} {\partial u’}\hat{u’}\right] dx + \mu\int_a^b gH(g)\left[\frac{\partial g}{\partial u}\hat{u} + \frac{\partial g}{\partial u’}\hat{u’}\right] dx = 0, \qquad \forall \hat{u}.

在上面的推导中，我们使用了这一事实。注意，我们在这里讨论的是非正性约束。非负性约束可以通过取约束方程的负，求解等价的非正性约束来处理。

上面变分方程的第一项是来自无约束问题的似曾相识的贡献。让我们看看如何使用 COMSOL 中的弱贡献节点添加惩罚项。我们将使用更简单的狄利克雷边界条件 节点来固定端点。

用罚函数法实现不等式约束。

注意，在上面的弱贡献中，我们没有包含，因为这个问题的约束只依赖于解，而不依赖于它的空间导数。

对一个递增的罚参数序列求解这个问题，同时重新利用前面的解作为初始估计，我们得到如下结果。

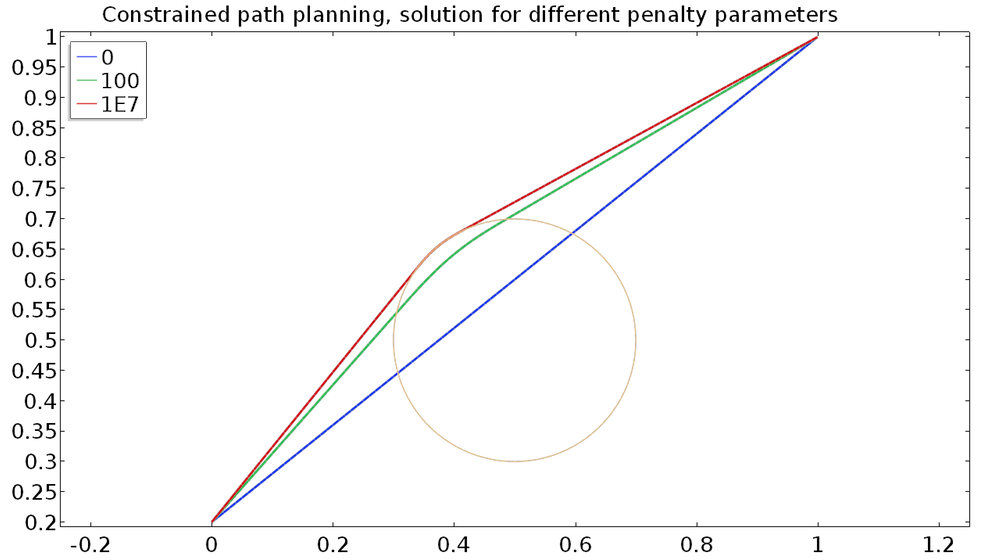
使用罚函数法寻找绕过障碍物的最短路径。零惩罚返回无约束解。

在讨论等式约束罚函数法的物理解释时，我们已经说过罚项引入了一个与违反约束成比例的反应。这种解释适用，但对于不平等约束，反应是片面的。

想象一下，使用压缩弹簧迫使一颗珠子留在原地。弹簧没有钩在珠上;他们只是接触。为了使珠子保持在x=0，我们必须在原点的每一边使用一个弹簧。如果珠子到原点的左边是可以接受的，那我们的约束是，我们必须只有右侧存在把压缩弹簧。这就是为什么我们惩罚是而不是。

一个弹簧的罚函数执行平等(多边)和不平等(单边)约束。

拉格朗日乘子法

在讨论不同约束执行策略的数值性质时，我们讨论过虽然拉格朗日乘子法严格执行约束，但它在数值解中有一些不受欢迎的性质。也就是说，它对解的初始估计很敏感，可能需要直接线性求解器。这些不利因素仍然存在，但在不平等限制下，还有一个额外的挑战。具体来说，就是约束可能并不总是活跃的。

考虑我们的路径规划问题。在不接触障碍物的部分路径中，约束是未激活的。然而，我们事先不知道哪些约束是有效的，哪些是无效的。有几种策略可以解决这个问题，下面我们只介绍两种常用的方法。

有效集策略

假设有些约束是有效的，有些不是。在一个分布式约束中，这意味着选择的点，并假设其他点在的可行区域内。在不活跃点，拉格朗日乘数应为零。在有效集上，拉格朗日乘数不应为负。这就是所谓的 Karush-Kuhn-Tucker (KKT) 条件。如果在计算后，有效集发生了变化或违反了 KKT 条件，我们必须适当地更新有效集并重新计算。下面的流程图总结了这一过程:

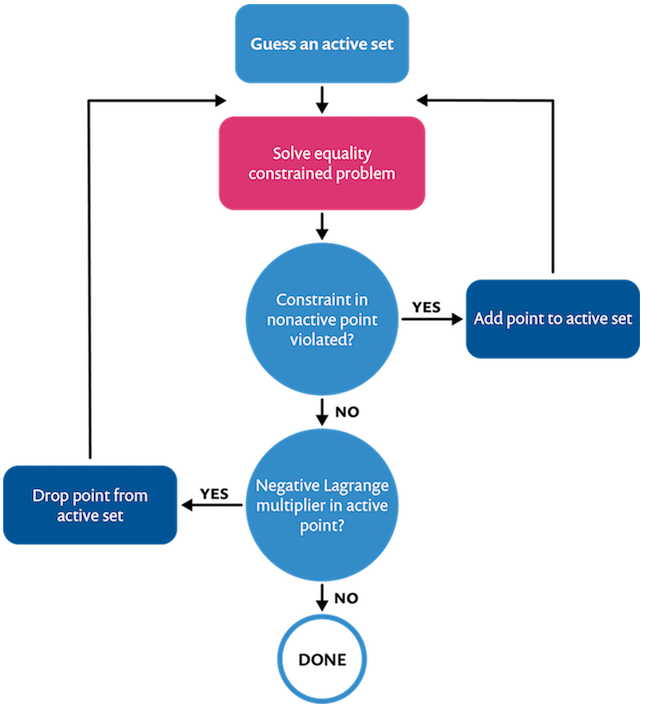
不等式约束的拉格朗日乘子执行的有效集策略。

通过这个迭代过程，每次迭代求解一个等式约束问题。等式约束的拉格朗日乘子实施已经在本系列的前一篇博文中讨论过了。

松弛变量

约束相当于。现在我们有一个引入新松弛变量的等式约束。如果不等式是分布式（逐点）约束，则松弛变量以及拉格朗日乘数都是函数。

一方面，松弛变量策略引入了另一个未知待解，但却一举解决了问题。另一方面，有效集策略不需要这个变量，但必须解决多个问题，直到有效集停止变化。

增广拉格朗日方法

就像我们处理等式约束一样，我们可以用一个微积分问题来讨论这个方法的基本思想。用拉格朗日乘数项、估计乘数项和惩罚项对无约束目标函数进行增广，得到

E_{\mu,\lambda} = f + \lambda^* g + \frac
{\mu} {2}\big\langle g\big \rangle^2.

这个约束条件的一阶最优条件为

\frac{df}{dx} + \lambda^* \frac{dg}{dx} +\mu \big\langle g \big\rangle \frac{dg}{dx} = \frac{df} {dx} + (\lambda^* +\mu \big\langle g \big\rangle )\frac{dg}{dx}
= 0.

这意味着乘数更新

\lambda^* = \lambda^* +\mu \big\langle g \big\rangle.

如果我们从对拉格朗日乘数的初始估计为零开始，那么上述等式仅在以下情况更新拉格朗日乘数是有效的。因此，拉格朗日乘数永远不会为负，并且仅在倾向于违反约束的点上为正。

增广拉格朗日方法是一种近似约束强制策略，将允许对约束的轻微违反。事实上，如果没有违反约束，拉格朗日乘数保持为零。因此，该策略完全满足 KKT 条件的双重可行性部分()，但仅近似满足互补松弛部分 ()。拉格朗日乘数法完全满足这两个条件。

不规则形状的障碍物

在今天的例子中，我们使用了一个非常理想化的湖泊，它的边界可以用一个简单的函数来描述。也可能是一个水池。有时，不等式约束有这样简单的解析形式。化学反应或种群动力学中的非负性约束就是这方面的例子。然而，其他约束没有这样简单的形式。

例如，在接触力学中，我们希望保持接触物体之间的间隙为非负值，但物体的边界很少如此简单，因此我们可以用平滑的解析函数来定义它们。最重要的是，对于大变形问题，我们希望在变形域上强制接触约束，但我们肯定没有对变形域的解析描述。因此，约束必须从满足离散版本的对象的网格下获得。当物体移动和变形时，必须使用复杂的搜索操作来找出哪些点与其他点接触或不接触。在 COMSOL Multiphysics® 软件中有用于这个和其他接触仿真程序的内置功能。

对于一些简单的几何形状和变形，我们可以使用广义拉伸算子来计算变形对象之间的距离，而无需使用接触力学功能。更复杂的几何图形才需要后者。

下一步

到目前为止，在本系列博客中，我们已经介绍了如何使用 COMSOL Multiphysics 解决有约束和无约束变分问题，并讨论了实施约束的不同数值策略的优缺点。也就是说，我们仅限于一维单物理场问题和变分问题，最多只有泛函中的一阶导数。

有了这个主题的基础知识，希望我们已经准备好处理高维数、高阶导数和多种领域的应用。这将在本系列的下一篇也是最后一篇博文中介绍。请继续关注!

查看更多关于变分问题和约束系列的博客文章

]]>

强制约束中数值问题的处理方法

Tue, 11 Sep 2018 05:29:56 +0000

在本系列博客的第一部分，我们讨论了如何通过简单的边界条件解决变分问题。接下来，我们将进行更复杂的约束，并使用拉格朗日乘子建立等效无约束问题。今天，我们讨论约束执行的数值问题。拉格朗日乘子法在理论上是精确的，但是在数值解的应用却有一定的挑战性。为了应对这个挑战，我们提出了 2 种缓解策略：罚方法和增广拉格朗日法。

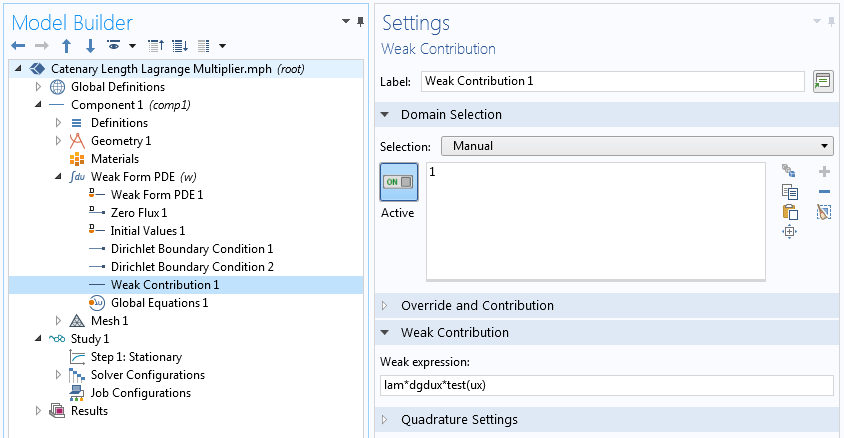
对全局约束使用拉格朗日乘子法

假设一条指定长度的均匀悬链线的形状为，悬挂在其自身重量下的单位长度的密度均匀的悬链线使函数值最小

E[u(x)] = \int_a^b u(x)\sqrt{1+u^{\prime}(x)^2}dx.

如果约束仅是边界条件，则可以自由调整悬链线的长度，以获得满足最终条件的最低势能。但是，如果我们要求悬链线具有指定的长度，于是就增加了全局约束

\int_a^b \sqrt{1+u^{\prime}(x)^2}dx = l.

如本系列博客的第二部分中所讨论的，对于拉格朗日乘子，该约束最小化问题可以转化为具有新自由度的无约束最小化问题。

\mathcal{L}[u(x),\lambda] = \int_a^b u(x)\sqrt{1+u^{\prime}(x)2}dx + \lambda \left[\int_a^b \sqrt{1+u^{\prime}(x)^2}dx – l \right].

请记住，全局约束中每个约束都具有单个拉格朗日乘子，而不是分布式（逐点）约束那样的字段。我们使用下式对此进行概括。

F = u(x)\sqrt{1+u^{\prime}(x)2}, \qquad g = \sqrt{1+u^{\prime}(x)^2}

通过将一阶变分导数和都设置为从到0，来推导一阶最优条件。有关变分导数的更多信息，请参阅读本系列博客的第一部分。

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F} {\partial u’}\hat{u’}\right]dx + \lambda\int_a^b \left[\frac{\partial g}{\partial u}\hat{u} + \frac{\partial g}{\partial u’}\hat{u’}\right]dx=0, \quad \forall \hat{u},

\hat{\lambda}\left[\int_a^b g(x,u,u’)dx – l \right]=0, \quad \forall \hat{\lambda}.

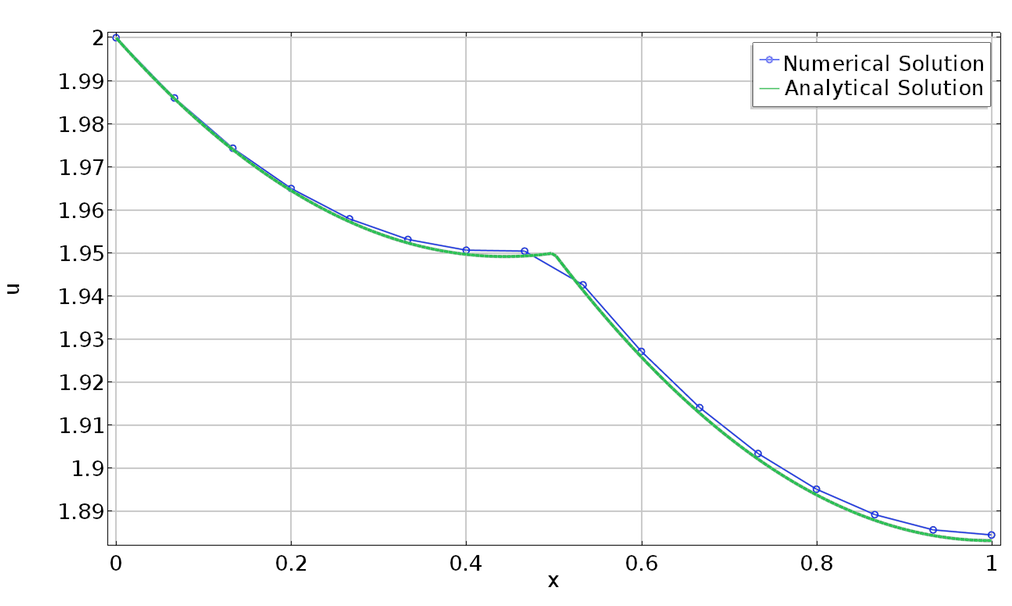
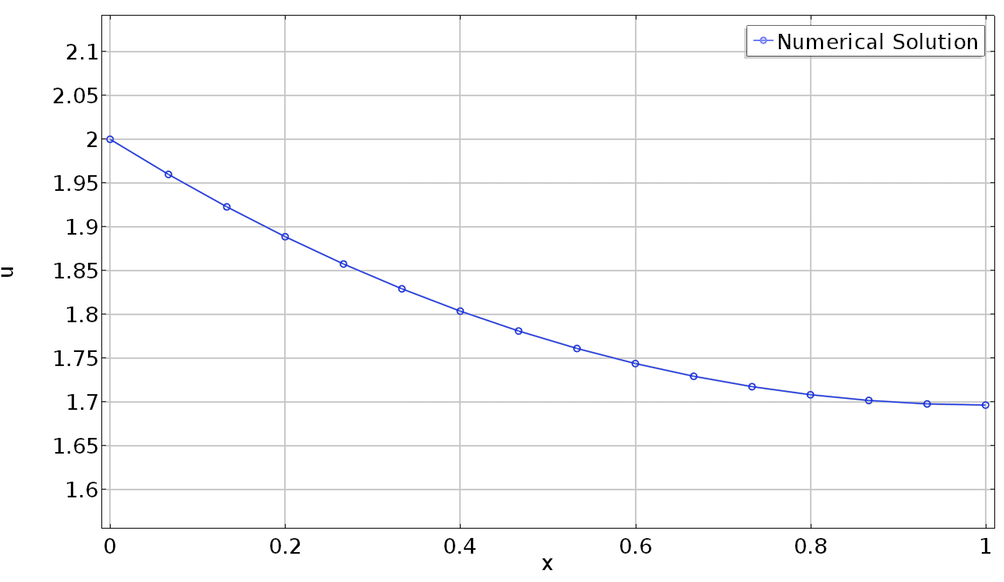
现在，我们来求解悬链线的形状，该悬链线分别悬挂在两个高 10 m和 9 m，相距 10 m的杆上，悬链线长 10.5 m。

两端狄利克雷（Dirichlet）边界条件也可以使用自己的拉格朗日乘子作为约束添加。在本系列博客的第二部分中，我们演示了如何执行此操作。本文中，我们主要讨论全局约束，使用内置的狄利克雷边界条件 节点来固定端点。

全局约束设置。

请注意，在上述弱贡献中，不包含项，因为只是的函数并不是的函数。

此时，尝试计算求解会生成错误消息。这是由当使用拉格朗日乘子法求解含全局约束或分布约束的非线性问题时一个常见数值问题引起的。对于一些试验解，有限元刚度矩阵（Hessian矩阵的优化）可以是单一的。因此，良好的初始值很重要。

应对该挑战的一种常用方法是将无约束问题的解用作约束解的初始估计。在 COMSOL Multiphysics® 软件中，这可以通过在同一研究中添加两个步骤并禁用第一个研究中的约束来实现。第一步的解将自动用作第二步的初始迭代。

使用无约束解作为约束问题的初始估计。

限定长度以及无约束的悬链线。

如果我们在结果 > 派生值>全局计算 中计算intop1（g），则该长度恰好为 10.5 m。拉格朗日乘子也可以在全局计算 中使用。原则上，此拉格朗日乘子与我们必须施加的张力有关，以使其维持所需的长度。

拉格朗日乘子的另一个常见数值问题是刚度矩阵中的正定损失。许多不受约束的变分问题都有正定刚度矩阵。此时，可以利用正定性的迭代线性求解器。使用拉格朗日乘子法执行约束会导致鞍点问题，并且相应的线性系统是不确定的。这个问题并不是不可以解决，我们可以使用直接求解器，但计算成本会很高。

我们已经设计出多种方法来避免在全局和分布式约束中拉格朗日乘子的数值缺点。在这里，我们只讨论 2 种使用最广泛的方法：罚方法和增广拉格朗日乘子法。

罚方法

约束最小化问题的惩罚性表述将拉格朗日乘子项替换为惩罚约束违反的项。在全局约束的情况下，罚目标函数为

E_{\mu}[u(x)] = \int_a^b F(x,u,u^{\prime})dx + \frac{\mu}{2} \left[\int_a^b g(x,u,u’)dx – l \right]^2.

如果罚因子太大，则上式中的第二项会使罚项太大，以至于对最小化总函数而言，满足约束条件非常必要。采用约束违反的平方，以便对长度的下冲和上冲都进行惩罚。因此，这是一个双向约束。相反，不平等约束是单向的。

在这里，罚因子是我们选择的，是唯一未知的。因此，一阶最优条件变为

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u}+\frac{\partial F}{\partial u’}\hat{u’}
\right]dx + \mu \left[\int_a^b g(x,u,u’)dx – l \right]\int_a^b \left[\frac{\partial g}{\partial u}\hat{u}+\frac{\partial g} {\partial u’}\hat{u’}\right]dx, \qquad \forall \hat{u}.

与拉格朗日乘子法相比，我们可以看到这种方法类似于用比例常数乘以约束违反来近似拉格朗日乘子。

\lambda \approx \mu \left[\int_a^b g(x,u,u’)dx – l \right].

如果我们将拉格朗日乘子视为维持约束所需的力，则罚方法提供了一种线性跳跃，当违反约束时会向后推，并确定跳跃常数。例如，如果我们的约束是温度，则罚方法将提供与试验温度和指定温度之差成比例的热通量，然后确定传热系数。

全局约束的罚执行示例。

罚方法易于实现，并且具有吸引人的数值特性。如果不受约束的刚度矩阵是正定的，那么它不会增加新的自由度并能保持刚度矩阵的正定性。但是，它也有缺点。例如，不能完全满足约束条件。为此，我们需要将罚参数设为无穷大，但是这无法在在数值上实现。实际上，一个有限但很大的罚项会使数值问题陷入困境。此外，非常大的罚参数使解过于关注可行性，而以最优性为代价。因此，诀窍是找到一个足够大的罚参数，以更好地近似约束条件，但又不要太大。

下面，我们看看罚参数的各种值对长度约束的满足程度。

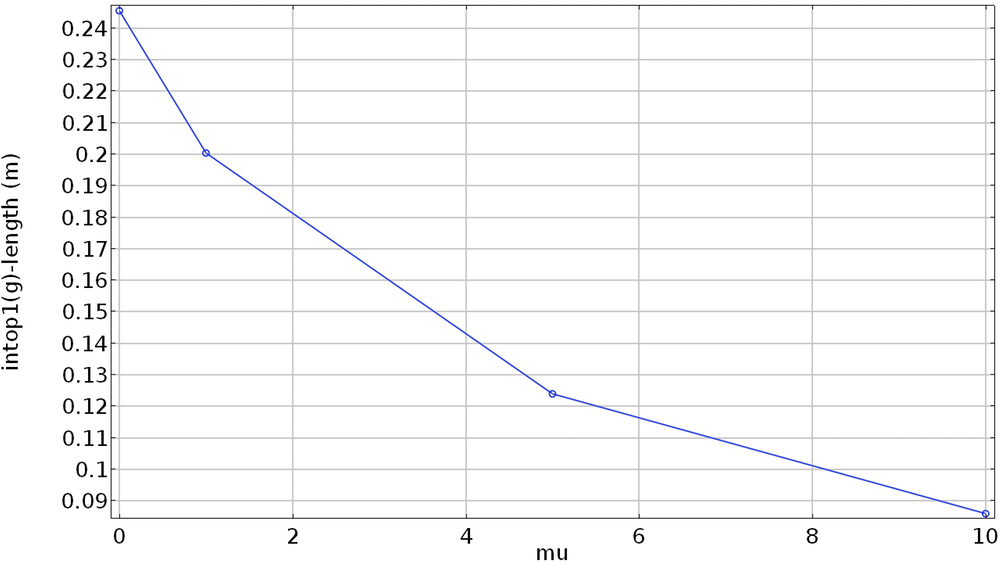
如果罚参数较高，则计算出的长度和指定长度之差将趋近于零。

从上图可以看出，罚因子越高，强制约束越好。但是，如果我们将罚因子设置为20，则会由于惩罚因子太高而出现收敛误差。

罚参数的辅助扫描

我们已经开发了一些算法来逐渐改善罚问题。一种简单的算法是逐渐增加罚因子，同时将之前罚参数的收敛解重新用作初始估计。

近似拉格朗日乘子包含约束违反和罚项的乘积。这样，当约束违反较小时，我们可以承受较大的罚参数，而不会使数值问题变得不适。因此，如果我们从其解近似满足约束条件的试验解开始，则可以使用更高的罚因子（与大量违反约束条件的试验解相比）。通过在罚参数上添加辅助扫描，可以轻松地在 COMSOL Multiphysics 中实施该策略。

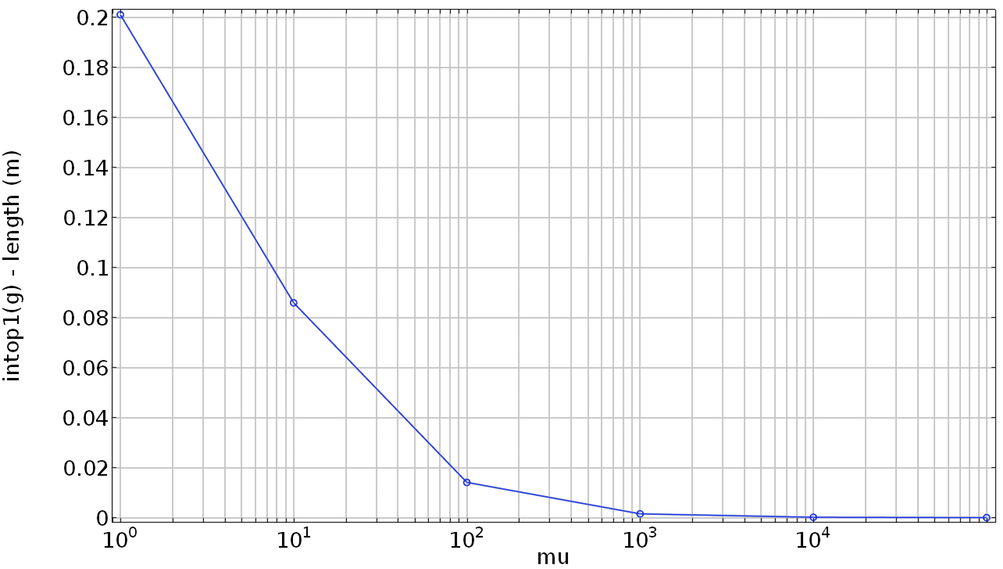
当使用辅助扫描罚因子时，计算长度与指定长度之差与罚因子之比。

如上图所示，对罚因子进行辅助扫描使我们能够使用更高的罚因子而不会产生不良情况，更重要的是，可以更好地执行约束。下图比较了这些连续解和拉格朗日乘子解的精确度。

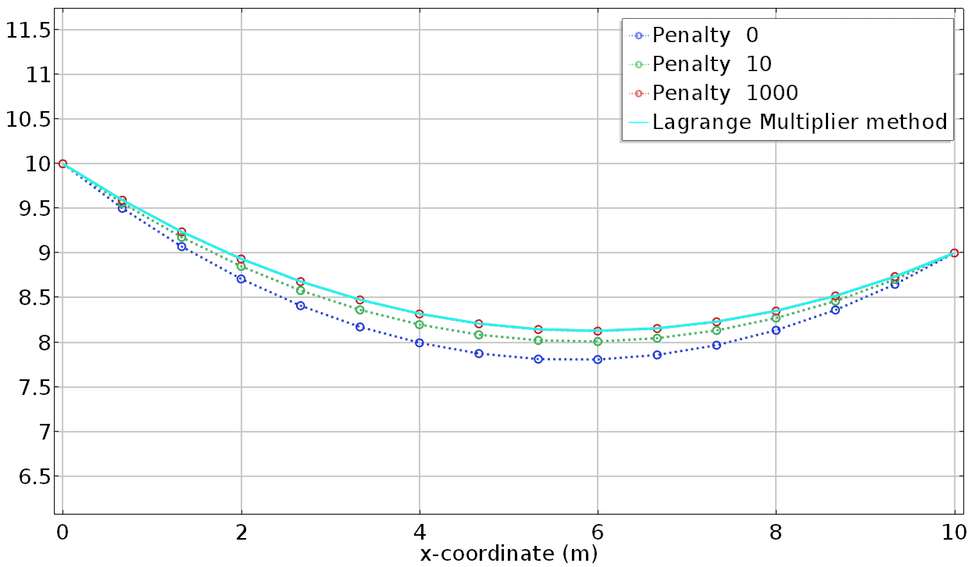
罚和拉格朗日乘子解的比较。

增广拉格朗日法

为了结合罚方法和拉格朗日乘子法的优点，同时避免它们的缺点，我们设计了增广拉格朗日法。为了清楚起见，我们从微积分问题开始。

对于问题

\textrm{minimize } f(x), \quad \textrm{subject to } g(x)=0.

拉格朗日乘子法可求解无约束问题

\mathcal{L}(x,\lambda) = f(x) + \lambda g(x),

而罚方法使用

E_{\mu}(x) = f(x) + \frac{\mu}{2}g^2(x).

增广拉格朗日法同时具有拉格朗日乘子和罚项。

E_{\mu,\lambda}(x) = f(x) + \lambda^* g(x) + \frac{\mu}{2}g^2(x).

在拉格朗日乘子法中，拉格朗日乘子为未知数；而在增广拉格朗日法中，从拉格朗日乘子的估计开始，对其进行迭代改进。

拉格朗日函数的一阶最优条件是

\frac{d}{dx} E_{\mu,\lambda} = \frac{df}{dx} + \lambda^* \frac{dg}{dx} +\mu g \frac{dg}{dx} = \frac{df}{dx} + (\lambda^* +\mu g )\frac{dg}{dx} = 0.

将其与拉格朗日乘子法的最佳条件进行比较，可以看出乘子的改进估计为

\lambda = \lambda^* +\mu g .

回到我们今天讨论的变分演算和全局约束，增广拉格朗日迭代为

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u}+\frac{\partial F}{\partial u’}
\hat

{u’}\right]dx +
\left(\lambda_k + \mu \left[\int_a^b g(x,u,u’)dx – l \right]\right)
\int_a^b \left[\frac{\partial g}{\partial u}\hat{u}+\frac{\partial g}{\partial u’}\hat{u’}
\right]dx, \qquad \forall \hat

{u}
.

\lambda_
{k+1}
=\lambda_k + \mu \left[\int_a^b g(x,u,u’)dx – l \right]

该迭代将继续进行，直到约束违反足够小（或等效，直到乘子停止明显变化）为止。初始拉格朗日乘子通常为零。请记住，解也由指引。上述方程式忽略了该值，以将注意力集中在拉格朗日乘子更新上。

通过在拉格朗日乘子中逐步积累越来越多的力（通量），增广拉格朗日方法可以很好地实施约束，同时保持较小的罚参数。增广拉格朗日法对于分布式约束特别有吸引力，因为每个点都可以根据局部条件进行不同的更新。

罚方法（不按顺序增加）和增广拉格朗日法是 COMSOL Multiphysics 中用于接触约束的内置方法，但是接触力学涉及不等式约束。在本系列博客的下一篇博客文章中，我们将展示如何在相应物理场中没有内置功能的情况下添加用户定义的不等式约束。

故意违反约束

有时我们想故意违反约束。假设在上面的示例中我们将长度约束设置为 10.04 m。这在物理上是不可能的，因为支座之间的最短距离（直线距离）为 10.05 m。

拉格朗日乘子法想要精确地执行约束，因此，这将导致收敛问题。但是，我们可能仍想在某种程度上违反约束条件来获得不精确的解。在这种情况下，约束不一致或存在多余约束时，拉格朗日乘子法就无法收敛。但是，我们可以使用近似约束方法（例如罚方法和增广拉格朗日法）来放宽约束并获得近似解。例如，多体动力学模块为关节提供了一种内置的罚方法，以使模型对过度约束不那么敏感。

后续操作

今天，我们已经证明了拉格朗日乘子法可以有效的正常工作。但是，它对解的初始估计更敏感，并且可能使不确定的潜在问题变得不确定，因此必须使用直接求解器。罚方法和增广拉格朗日乘子法克服了这些困难，以换取一些对约束的违反。

我们希望可以精确地执行约束，但是在约束不一致或过多的问题中，我们可能希望不精确地强制执行约束以获得一些近似解。在下一篇博客文章中，我们将讨论不平等约束。拉格朗日乘子法还会产生不平等约束的缺点。

本系列博客，我们更多的介绍了罚方法，并集中讨论了一维和单个未知问题。在即将发布的另一篇博客文章中，我们将讨论多个维度、多个字段和高阶导数。

单击下面的按钮联系 COMSOL ，了解有关 COMSOL Multiphysics 中基于方程的建模功能的更多信息。

联系 COMSOL

查看更多有关“变分问题和约束”问题的系列博客文章

]]>

在变分问题中指定边界条件和约束

Fri, 07 Sep 2018 02:35:31 +0000

在本博客系列的第一部分中，我们讨论了变分问题，并演示了如何在 COMSOL Multiphysics^® 软件中使用简单的内置边界条件解决它们。今天，我们将讨论更通用的边界条件和约束,并展示如何使用第一部分（皂膜）中的相同变分问题以及同样的数学方法，在 COMSOL^® 软件中实现这些边界条件和约束。

约束分类

对约束进行分类有多种方案。在这里，我们将考虑对计算实现影响最大的那些。

基于相关的几何实体，可以有点（孤立）、分布和全局的约束。例如，一方面，一维问题中的边界条件是在孤立点处的约束。另一方面，应该在每个点都满足的条件是分布式约束。全局约束指定了解的一些标准（通常是一个积分）。例如，指定悬链线的长度或肥皂膜的表面积来提供全局约束。

有些人将术语“逐点约束”用于分布式约束。这里，我们将其与“点约束”做一个明显的区分。点约束在单个点或有限数量的孤立点处执行点约束，这组点没有长度、面积或体积。但是，分布约束在域的每个点上都有效，可以是三维对象的边、面或域的每个点。

另一种分类是等式约束与不等式约束。接触力学中出现了结构力学中常见的不等式约束。装配体中接触对象之间的间隙必须为非负。在化学反应工程中，物质浓度的下界也是不等式。

这些分类也会重叠。例如，我们可以具有分布式的不等式约束和分布式的等式约束，等等。不等式约束在数学上更具挑战性，因此，我们先讨论等式约束，然后在本系列的后面部分中继续讨论前者。

等式约束理论简介

对于微积分问题

\textrm{最小化}\qquad f(\bf{x}), \qquad \textrm{使}\quad g(\mathbf{x})=0

我们可以通过找到关于坐标和拉格朗日乘子的扩展目标函数的驻点来求解

\mathcal{L}(x,\lambda) = f(\bf{x}) + \lambda g(\bf{x})

尽管有适当的扩展, 在变分演算中也使用了相同的方法。对于以下问题

\textrm{求函数} u(x) \textrm {的最小值}
E[u(x)] = \int_a^b F(x,u,u^{\prime})dx,

\textrm{ 对于所有 x 满足} g(x,u,u^{\prime})=0 \textrm.

分布式约束必须满足域当中的所有点，而不仅仅是某一点。因此，每个点都将会有自己的拉格朗日乘子，使成为一个函数，而不仅仅是一个数字。因此，增广函数如下

(1)

E[u(x),\lambda(x)] = \int_a^b [F(x,u,u’)+\lambda(x)g(x,u,u’)]dx.

在将约束变分问题从一个场转换成不受约束问题的两个场和之后，我们将寻找最优准则。我们可以通过在求解场和拉格朗日乘子场中都做独立的变分，来找到一阶最优准则

\frac{d}{d\epsilon_1}E[u+\epsilon_1 \hat u,\lambda+\epsilon_2 \hat{\lambda}]\bigg|_{(\epsilon_1=0,\epsilon_2=0)} = 0, \quad
\frac{d}{d\epsilon_2}E[u+\epsilon_1 \hat u,\lambda+\epsilon_2 \hat{\lambda}]\bigg|_{(\epsilon_1=0,\epsilon_2=0)} = 0.

对于和，有

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F}{\partial u’}\hat{u’} + \lambda(\frac{\partial g}{\partial u}\hat{u} + \frac{\partial g}{\partial u’}\hat{u’})\right]dx=0,

\int_a^b \left[\hat{\lambda}(x)g(x,u,u’)\right]dx=0.

这些是我们需要在“弱形式偏微分方程”接口中输入的方程式。首先，我们推导出全局（积分）约束和点（孤立）约束的相应条件。

当有全局约束时

\int_a^bg(x,u,u^{\prime})dx=G,

增广函数是

E[u(x),\lambda] = \int_a^b F(x,u,u^{\prime})dx+\lambda\left[\int_a^b g(x,u,u^{\prime})dx-G\right],

这里，是一个数字而不是场。

一阶最优条件是

\hat{\lambda}\left[\int_a^b g(x,u,u’)dx-G\right]=0.

最后，使用费米-狄拉克函数的属性，点（孤立）约束可以看作全局约束

\int g(x,u,u^{\prime})\delta(x-x_o)dx=0.

同样，我们可以类似地利用费米-狄拉克函数来推导二维和三维中的边以及三维中曲面的约束。

将上述结果插入到全局约束的公式中，得到一阶最优条件

(2)

\int_a^b \left[\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F}{\partial u’}\hat{u’}
\right]dx + \lambda\left[\frac{\partial g}{\partial u}\hat{u} + \frac{\partial g} {\partial u’}
\hat{u’}\right]_{x=x_o}=0,

(3)

\hat{\lambda}g(x_o,u,u^{\prime})=0.

如果我们有多个孤立点约束，则每个点都有一个拉格朗日乘子。拉格朗日乘子将不是一个场，而是一组有限的标量，在每个孤立点上都有一个有效标量。如果我们的分布约束不是施加在整个域上，而是施加在部分域上，则只能在那部分上定义拉格朗日乘子。最后，我们将有一个拉格朗日乘子场。

在 COMSOL Multiphysics^® 中施加约束

现在让我们看看如何在 COMSOL Multiphysics 中施加约束。仍以之前博客文章的皂膜问题为例，但施加了以下边界条件。

u(a) = 2, \quad u^{\prime}(b)=0.

第一个边界条件是可以使用“狄利克雷边界条件”节点指定，但是出于教学原因，我们将使用更通用的约束框架。上面的两个边界条件可以重写为

g(a,u,u^{\prime})=u-2 =0, \quad g(b,u,u^{\prime})=u^{\prime} =0.

我们需要约束方程对和求偏导。

\textrm{At } x=a, \frac{\partial g}{\partial u}=1, \frac{\partial g}{\partial u^{\prime}}=0,

\textrm{At } x=b, \frac{\partial g}{\partial u}=0, \frac{\partial g}{\partial u^{\prime}}=1

最后，我们将在相应的点上将这些作为弱贡献插入。来自的贡献保持与以前相同。

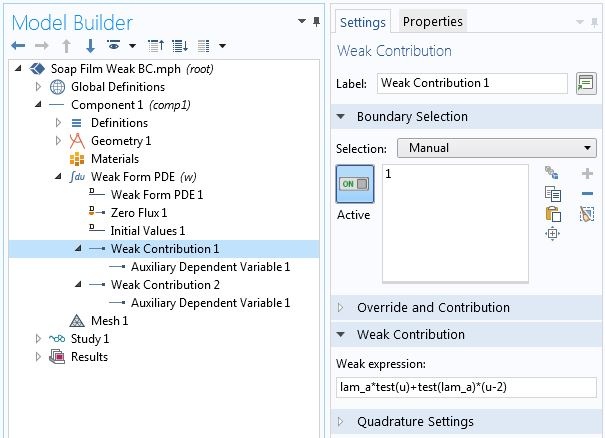
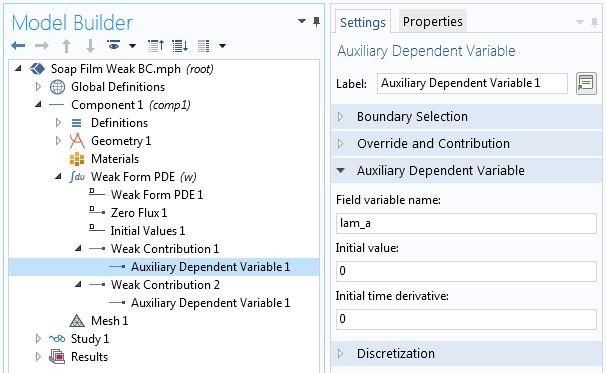
使用点弱贡献指定点约束。

注意，等式3 和等式2 的第二项当中的点贡献都已经被加到“弱贡献”1当中。这里的逻辑是，因为和是独立变分，将包含这些变分的项之和设置为零等同于将包含每个变分的项设置为零。下图显示了具有上述约束的变分问题的数值解。

左端半径为 2，右端半径为零的解。

在理论部分，我们讨论了不同类型的约束。下表总结了软件中的推荐位置，这些位置指定了约束的贡献，并根据约束的类型定义了未知数（拉格朗日乘子）。

约束类型	例子	约束贡献包含	约束贡献包含	在哪里定义
分布式约束	对材料行为的约束解的上限或下限二维和三维问题中的边界条件	弱贡献	弱贡献	辅助因变量弱贡献下的属性
全局（积分）约束	边长物体重量表面平均位移（温度）	弱贡献	“全局方程”节点	“全局方程”节点
孤立点约束	一维边界条件约束在孤立的内部点上	弱贡献	弱贡献	辅助因变量弱贡献下的属性

指定通量（力）

接下来，我们讨论指定约束条件。为此，我们引入了未知的拉格朗日乘子。在许多物理问题中，拉格朗日乘子是增强约束所必需的反作用力或通量。如果知道作用力或通量而不是约束，如何指定呢？

我们需要回到要最小化的函数并重新计算，包括力（通量）。例如，对于结构力学中的边界载荷，会由于载荷而增加虚拟功。在COMSOL Multiphysics接口中输入的表达式类似于我们对约束所做的事情。用已知的力（通量）代替了拉格朗日乘子，我们不需要拉格朗日乘子作为辅助变量。结果是，包含拉格朗日乘子变化的项消失了。

阅读之前的博客文章，了解有关如何使用弱贡献>添加点载荷（源）的更多信息。

将约束添加到不在几何序列中的点

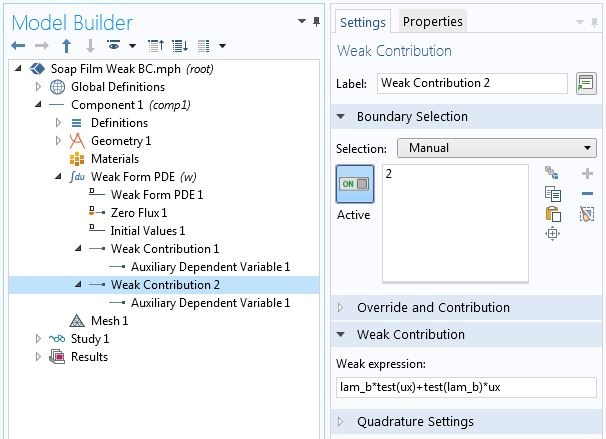
有时，我们希望向域中未在几何序列中显式插入（或通过曲线的交点创建）的点添加约束。如上例所示，我们无法选择点并将其与点弱贡献关联。但是，我们可以添加全局弱贡献，并使用域探针来引用解及其变体。

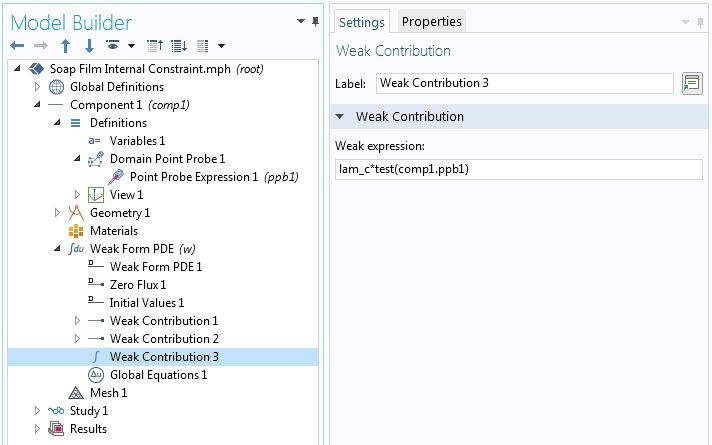
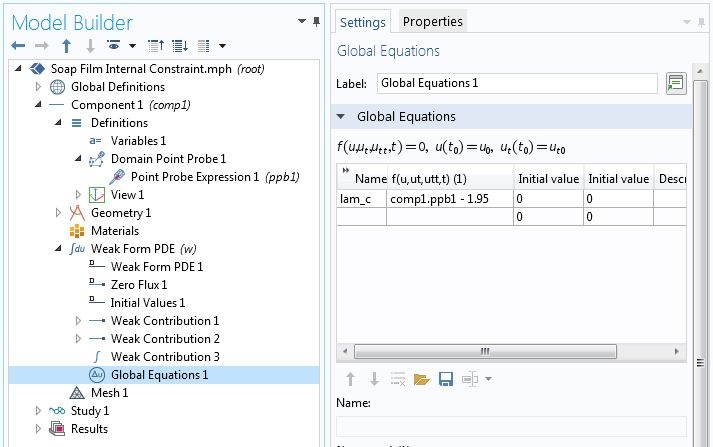
例如，对于两端支撑的悬链线。每单位长度重量均匀的电缆的变分问题与轴对称皂膜问题相同。因此，我们将使用相同的 COMSOL 模型。另外，我们希望限制中心高度为 1.95，而无需在几何序列中添加点节点。首先，我们为增加了一个域点探针。探针的名称命名为 ppb1 。对应于(等式1) 的弱贡献为 lam_c * test（comp1.ppb1)，其中 lam_c 是新的拉格朗日乘子。如下面截图所示，我们在全局“弱贡献”节点中输入此贡献。与显式定义的几何实体上的弱贡献相反，此节点不允许创建辅助变量。但是，我们可以添加一个全局方程 节点，在其中可以定义拉格朗日乘子并指定约束。

为不在几何图形中的点添加约束。

下图显示了包含该约束的解。在网格节点处添加了圆。左图显示了中心点没有与之关联的网格节点的情况。这样，仅近似满足该约束。在右图中，我们可以看到在更细的网格上解的情况，网格剖分器在想要施加约束的地方添加了节点。在此，严格满足约束条件。

验证不在几何序列中的点的内部约束。绘图中未保留纵横比。

我们还可以使用类似的策略来增加点载荷（源），以解决诸如结构力学、传热或化学传递等问题。如前所述，这些负载在数学上对应于拉格朗日乘子。如果我们知道拉格朗日乘子，则不添加全局方程式。相反，我们只有弱贡献，并且代替上面的 lam_c，我们键入了施加的机械、热、化学或其他类型的载荷。

敬请关注！

到目前为止，在本博客系列文章中，我们已经展示了如何使用“弱形式偏微分方程”接口解决变分问题以及如何包含等式约束。

约束在数值解中引入了额外的复杂性，最主要的是，它们导致了鞍点问题，并且拉格朗日乘子实施破坏了刚度矩阵的正定性。对于非线性约束，在非线性迭代期间会出现存在奇异矩阵的危险，尤其是在全局和分布式约束中。

在本系列博客的下一部分内容中，我们将介绍求解这些问题的数值策略。在使用等式约束讨论了这些策略之后，将在后续中讨论不等式约束。

查看“变分问题和约束”系列博客的更多博客文章

]]>

肥皂膜及其他变分问题建模概述

Tue, 04 Sep 2018 08:38:10 +0000

肥皂膜、悬链线电缆和光束有什么共同点？它们都有着使某些数量最小化的行为方式，这类问题普遍存在于生物学、经济学、弹性理论、材料科学和图像处理等科学和工程领域。我们可以使用 COMSOL Multiphysics^® 软件中的内置物理场接口模拟很多这样的问题，在变分问题和约束系列博客中，我们将向您展示如何使用基于方程的建模功能解决变分问题。

函数的最小值

在初等微积分中，我们为单变量或多变量函数寻找最优值，即，寻找一个单一的数字或一组有限的数字使函数最小（或最大）。在变分法中，我们寻找一个函数使泛函最小（或最大）。从某种意义上说，我们可以认为这是无限维优化。粗略地讲，就是泛函取一个函数并返回一个数值。例如，定积分就是一个泛函。

在工程问题中，这些泛函通常代表某种能量。例如，在弹性理论中，我们可以通过最小化总势能来找到平衡解。这个术语经常被用在其他变分问题上，例如变分图像处理。我们称泛函为“能量”——即使它在物理上不代表通常意义上的能量。

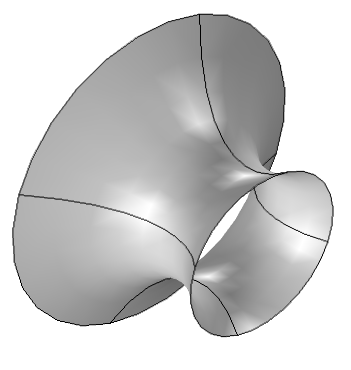
两个环之间的肥皂膜。

考虑 yz 平面上两个圆环之间的肥皂膜，其中心在 x 轴。我们希望找出这样一个函数，当我们绕 x 轴旋转它时，可以获得肥皂膜的形状。这个函数实际上是下面这个泛函的最小值，

(1)

E[u(x)] = \int_a^b u(x) \sqrt{{1+u^{\prime}(x)^2}}dx.

更一般地说法是，在变分法中，我们正在寻找一个函数，使泛函的值最小，

(2)

E[u(x)] = \int_a^b F(x,u,u^{\prime},u^{\prime\prime},\ldots)dx.

大多数工程问题处理的是最多包含一阶导数的泛函。在本系列博客的开始，我们将在一个空间维度上关注这些问题。稍后，我们将推广到高维度、高阶导数和几个未知数。最后，由于最大值和最小值本质是一样的，因此我们将在后续文章中只讨论最小值。

除非另有说明，否则我们将处理的泛函是

(3)

E[u(x)] = \int_a^b F(x,u,u^{\prime})dx.

求解变分问题

假设你发现自己被蒙住了眼睛进入一个山谷中，你怎么知道已经到达底部？（顺便说一句，摘掉眼罩不算）。你可能会用手和脚感觉周围的地面，如果你测试的每个区域都感觉都比你站的地方高，那么你就站在山谷的底部（至少是在一个局部的洼地）。在微积分和变分法中，同样的思想被用来检查最小值。在微积分中，我们测试相邻点，而在变分法中，我们测试相邻函数。

当且仅当对于微小值以及每一个容许变分都遵循以下表达式时

(4)

E[u+\epsilon \hat{u}] \ge E[u(x)]

函数使得泛函最小。

不是每个变分是可接受的，因为每一个都必须满足解的约束条件。例如，对于两端固定在线上的肥皂膜，我们用于与最小函数进行比较的每个函数也必须固定在线上。因此，我们只考虑那些满足的变分。我们将在后面的博客文章中详细讨论约束。

假设有足够的平滑度来进行微分，方程4 的必要条件是

(5)

\frac{d}{d\epsilon}\bigg|_{\epsilon=0}E[u+\epsilon \hat u] = 0,

在本系列中，我们不打算讨论移动或开放边界的问题。在这种情况下，我们可以把微分移到积分内部，并应用链式法则得到

(6)

\frac{d}{d\epsilon}\bigg|_{\epsilon=0}E[u+\epsilon \hat u] = \int_a^b [\frac{\partial F}{\partial u}\hat{u} + \frac{\partial F}{\partial u’}\hat{u^{\prime}}]dx=0.

请注意，我们只改变因变量和它的导数，而不是空间坐标。

如果您对移动边界或界面的问题感兴趣，请查看博客文章：使用 COMSOL Multiphysics^® 模拟自由液面的两种方法和在 COMSOL Multiphysics^® 中用动网格为自由液面建模。

如方程1 所示，对于肥皂膜，我们有。因此，肥皂膜的变分问题是找到，以使

(7)

\int_a^b [\sqrt{1+u’^2}\hat{u} + \frac{uu’}{\sqrt{1+u’^2}}\hat{u’}]dx=0, \forall \hat{u}.

欧拉-拉格朗日方程

在经典变分法中，我们应用分部积分从变分中移动空间微分到解以获得欧拉-拉格朗日方程

(8)

\frac{\partial F} {\partial u}-\frac{d} {dx}(\frac{\partial F}{\partial u^{\prime}})=0,

并利用常微分方程（ODE）方法求其解。

在高维空间中，欧拉-拉格朗日方程变成了偏微分方程。

在我们的例子中，我们不需要使用欧拉-拉格朗日方程，所以不再进一步讨论它，原因是使用有限元方法来求解变分公式。例如，在 COMSOL Multiphysics 中，如果我们使用系数形式偏微分方程 或者一般形式偏微分方程 接口指定欧拉-拉格朗日方程，软件会在内部指定并求解相应的变分方程，既然如此，就没有必要再浪费精力吧？正如我们将在后面看到的，变分形式还提供了很自然地考虑求解域和边界条件的方式。

在 COMSOL Multiphysics^® 中执行一个变分问题

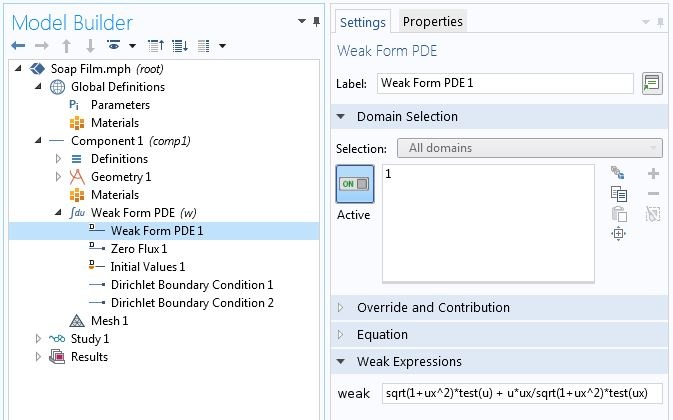
为了说明 COMSOL Multiphysics 中的变分问题，我们使用了弱形式偏微分方程 接口。那我们如何来对解以及相应的试函数求微分呢？对于后者，我们可以使用试函数算子。例如，对于肥皂膜问题，变分公式中的被积函数在弱形式偏微分方程 节点输入为 sqrt(1+ux^2)*test(u)+u*ux/sqrt(1+ux^2)*test(ux)，如下所示。

指定一个变分问题。

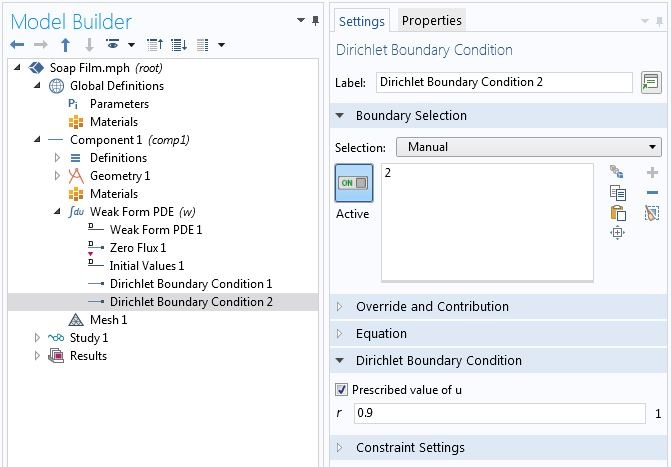
我们考虑一个简单的约束，即肥皂膜固定在左右两边的金属丝环上，左环和右环的半径分别是 1 和 0.9，因此我们知道主变量在两端的值，可以使用狄利克雷边界条件 节点指定这样的边界条件。出于数值的原因，在这个特殊的问题中，我们提供了初始值 1 替代默认的初始值 0。

使用狄利克雷边界条件节点指定已知的边界值。

如果我们求解，可得到下图所示的形状。

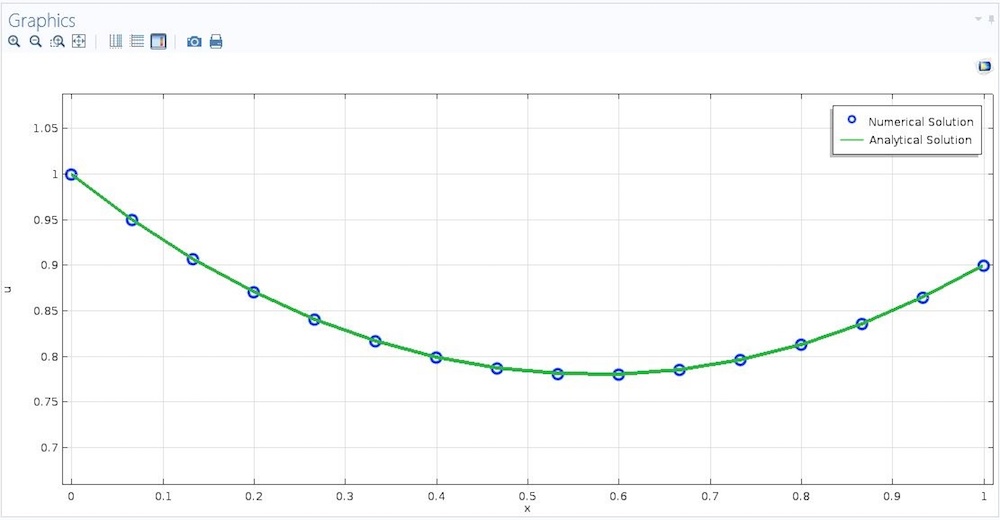
挂在两个垂直圆环之间的肥皂膜的轮廓。

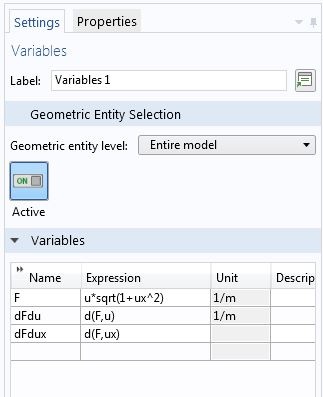
指定一个更通用的符号形式

在上面的例子中，我们手动对分别推导了和的偏微分，而利用 COMSOL Multiphysics 的符号数学能力，我们可以避免不必要的工作和潜在的错误。

用符号微分形式表达减少手动工作。

变分解与直接优化

我们还可以通过直接优化求解函数极小化问题。在这种方法中，我们不需要导出变分问题，但不利的一面是，它需要更多的计算工具。例如，在 COMSOL Multiphysics 中，直接优化需要优化模块。如果您对直接优化感兴趣，请查看我们的博客文章：如何求解两点间的最速降线。

后续操作

今天，我们向您展示了如何使用 COMSOL Multiphysics 软件中的弱形式偏微分方程 接口，您可以在弱形式概述这篇博文中了解更多关于弱形式的信息。

在接下来的文章中，我们将展示如何添加更复杂的约束，例如点约束、分布式约束和积分约束。本系列博客将逐步介绍更高的空间维度、更高阶的导数和更多物理场。敬请关注！

同时，您可以通过下面的按钮联系我们，了解更多关于 COMSOL Multiphysics 基于方程的建模特性。

联系 COMSOL

查看变分问题和约束系列中的更多博客文章

]]>

借助模型方法自动完成物理场选择和研究

Wed, 28 Jun 2017 02:08:20 +0000

想象一个场景：您在某些假设前提下求解了一个模型，却在分析结果时发现这些假设不成立，所以不得不添加新的物理场特征或改变研究类型来修正分析。那么，如何将这一过程自动完成呢？今天，我们将讨论如何使用 COMSOL Multiphysics® 软件 5.3 版本中新增的模型方法 功能来实现这一自动操作。

自定义求解过程的优势

我们经常会根据部分信息做出建模决策。例如，流体流动会一直保持层流状态还是会变成湍流？固体会保持弹性，还是会在指定的载荷和约束下变成塑性？变形是否大到应当运行几何非线性分析，还是适合小变形理论？有时，极限分析可以解答这些问题。如果我们能在求解之前知道问题的答案，就可以直接选择合适的模型。如果不能，一个低成本的办法是先求解简单模型，然后只有在求解无效的情况下，才切换为更复杂的模型。

举例来说，第一步完成弹性分析，然后只有当第一个分析得到的最大应力高于弹性极限时，才转换为弹塑性分析。类似地，先假设求解层流，然后在第一个分析得出的雷诺数足够高的情况下，再在模型中引入湍流。

根据初步结果，有时我们不得不改变建模方法，所以工作流程自动化可以减少大量工作。第一项研究所输出的信息还可以重复使用，以提高后续研究的计算效率。今天，我们将演示如何通过编写代码来自动完成弹塑性分析。代码会运行弹性分析，检查最大应力是否超过材料的屈服应力，并在必要时运行塑性模型。

在 COMSOL Multiphysics® 中创建模型方法

在 Windows® 操作系统平台中使用 COMSOL Multiphysics® 软件时，您可以开发拥有自定义用户界面的仿真 App，并通过编写方法添加更多功能。在Windows® 系统中构建的仿真App，可在任意操作系统中运行，还支持与同事、客户和学生们分享。

在 COMSOL® 软件的 5.3 版本中，我们发布了一个名为模型方法的新功能。它支持通过在 COMSOL Multiphysics 图形用户界面（GUI）中编写代码来扩展软件功能，即使您不打算开发 App 也可以使用它。“App 开发器”中的录制代码、编辑器工具、语言元素 和模型表达式 功能可以帮您轻松地生成编写模型方法所需的 Java® 代码。

要添加模型方法，请打开 开发工具选项卡，然后单击 运行模型方法，并选中一个方法。

要运行模型方法，请打开 开发工具选项卡，单击 运行模型方法，然后选择一种方法。

在之前发布的博客中，我们讨论了模型方法的运行机制，并演示了如何使用它创建随机几何。今天，我们将把这个主题延伸到物理场和研究设置中。

利用模型方法自动完成弹塑性分析

为了演示如何在物理场选择和研究序列中使用模型方法，我们选择以“案例库”中带孔板的弹塑性分析模型为例。示例模型是在预先判断压力必然超过弹性极限的前提下设置的，所以在分析中引入了塑性。今天，我们将编写一个模型方法，它能够自动检查材料属性的临界转变，如果确定塑性是必要条件，可自动引入这一属性。

我们预期自动执行的过程包含以下步骤：

运行无塑性的弹性研究。
检查最大应力是否超过材料的初始屈服应力。
如果最大应力小于初始屈服应力，则停止。反之，运行弹塑性研究。
如果塑性是必要条件，则重复使用弹性研究中的信息，以避免在弹性范围内执行冗余的非线性分析。

我们添加了两个研究，并在第一个研究中禁用了塑性。在第二个研究中，我们在弹塑性分析中增加了一个辅助扫描 来进行载荷递增。在第一个研究中，我们在全局定义 中将 para 设置为 1，从而施加了满载荷。在第二个研究中，我们利用参数 p_low 和 p_next 使研究生效。这些参数设定均基于第一次研究的结果。

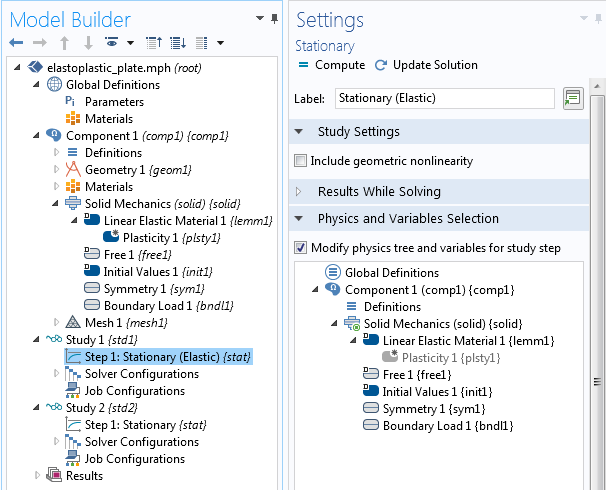
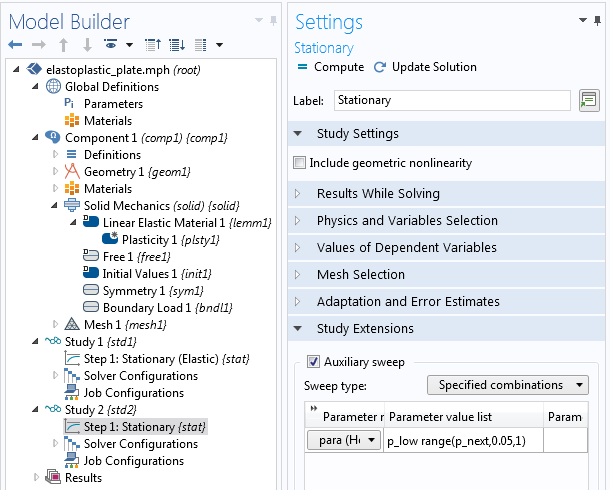
第二个研究只有在第一项研究中的假设不正确时才会开始进行计算。

在结果栏中，我们添加了一个派生值 节点来评估第一项研究中的最大应力。这一步骤也可以使用最大组件耦合 算子来完成。以帕斯卡为单位（如表面最大值 1 的“设置”窗口所示）的最大应力值将与同样以帕斯卡为单位的初始屈服应力值进行比较。为此，我们引入了参数 SY_scaled。

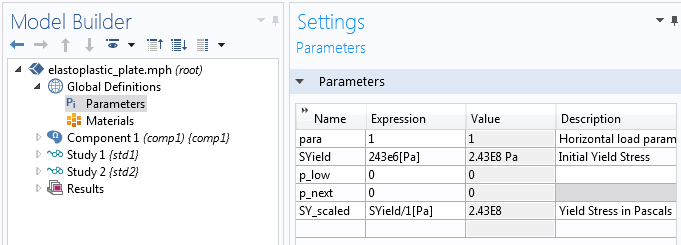
SYield 和 SY_scaled 分别应用到 材料节点和模型方法。

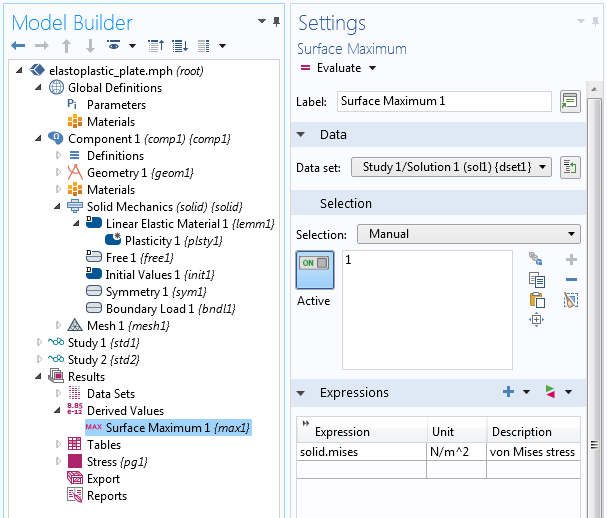
最大组件耦合算子可以替代此项操作。

现在我们获得了所需的全部数据，下面可以开始编写模型方法。

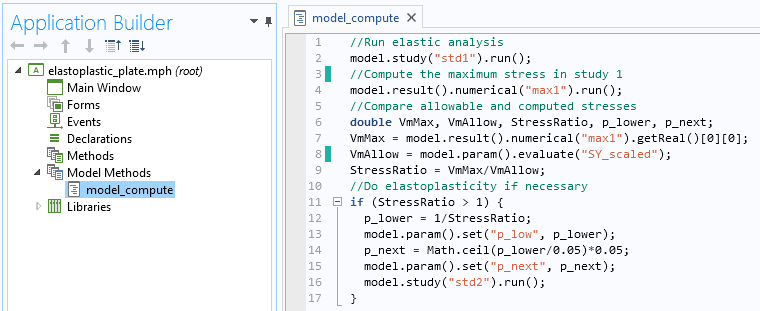
用于自动进行有效弹塑性分析的模型方法。

上图中，两行代码需要进行简要的说明：

第 12 行：
- 第一个研究是使用载荷参数 1 而完成的。如果第 9 行中的 StressRatio 大于 1，其倒数可以帮助我们得到弹性极限下的载荷参数。请注意，在此例中，我们能这样做的原因是：塑性是此问题中唯一可能的非线性。此模型中不存在几何非线性或接触。
第 14 行：
- 如果需要引入塑性，我们选择以 0.05 的步长完成辅助扫描。我们使用 Java® Math 类中的 ceil（向上取整）方法来获取载荷参数的最小值，该值是 0.05 的倍数，并且超过了上述弹性极限下的载荷参数。

根据这些信息，第二个研究（如果需要的话）只需在弹性区域内求解一次，也就是弹性极限处。我们可以在结果栏中查看使用了哪些载荷参数值。

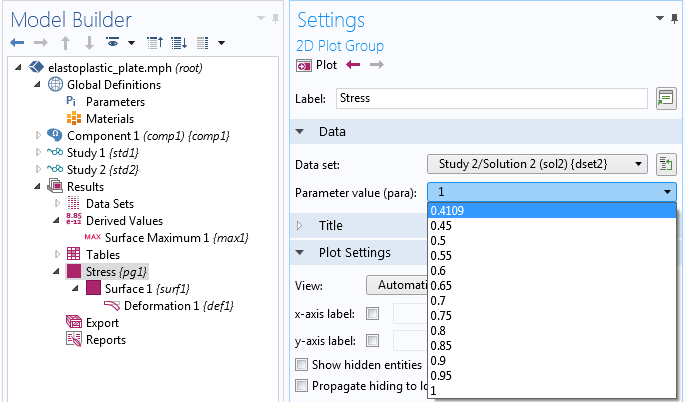
使用弹性研究来计算参数的最小值（突出显示）。

如果返回全局定义，就可以看到模型方法对初始值为零的参数 p_low 和 p_next 进行了更新。

基于初步研究的结果，借助模型方法修改参数值。

结束语

在本文中，我们展示了如何借助方法建立高效的物理场选择和研究序列。此类任务可以通过编程来完成。不过，用户也可以借助模型方法，轻松地使用“App 开发器”中的相同功能来获取所需的模型对象和方法。必要时，这些方法可以通过常规的 Java® 类（例如第一个示例中使用的 Math 类）或自定义的类进行扩展。

有关演示模型方法在物理场和求解器设置中的应用，我们只展示了一种操作方式。当然，您可以选择其他方式和改进的方法。举例来说，当分析弹塑性时，我们在“模型开发器”中添加了两项研究，这时您也选择使用单个研究，然后通过模型方法启用或禁用研究中的塑性和辅助扫描特征。

在以上案例中，我们必须在研究之间做出合乎逻辑的决策。如果您不打算做出决策，只是计划简单地参考另一个研究（比如，使用一个研究作为后续研究的预计算步骤），那么可以使用研究参考 功能。详细信息请参阅 COMSOL Multiphysics Reference Manual 中的研究参考 一节。

如果您对本文讨论的内容或 COMSOL Multiphysics 的使用操作有任何疑问，请通过下面的按钮与我们联系。

联系 COMSOL 进行软件评估

如何在 COMSOL Multiphysics® 中为求解器添加停止条件

Wed, 17 May 2017 05:06:51 +0000

有时，一个仿真运行的时间太久超过了所需的时间，从而使我们无法监控中间结果或有条件地停止运行。这可能会使我们不得不紧紧盯着监视器，随时准备“突袭”。本篇博客，我们将讨论如何在 COMSOL Multiphysics^® 软件中自动执行此过程。这样，我们可以忙其他的事情，而软件会在每个步骤之后检查条件。另外，我们还可以选择查看首次违反条件时发生的情况。

停止条件：何时以及如何使用

当满足或违反某个条件时，我们通常希望停止瞬态或参数化求解器。但是我们通常不知道停止条件将要发生的确切时间或参数值。在这种情况下，我们首先需要指定一个足够大的求解时间或参数范围，以便可以合理确定停止条件将被激活。然后，再添加停止条件以终止求解器。

一些物理条件（包括许用应力、温度极限和反应中的物质损耗等）或者计算问题（例如求解器采用的时间步长很小）可能会触发停止。

在 COMSOL Multiphysics 中，可以将停止条件添加到以下求解器：

瞬态求解器
频域求解器
带有参数或辅助扫描的稳态求解器

第一步是定义一个可以在关系或逻辑表达式中使用的标量。此标量可以是在某个感兴趣的点定义的一个量，也可以是一个全局的量，例如域或边界上变量的积分、最大值、最小值或平均值。在 COMSOL 软件中，我们可以使用点探针或组件耦合进行定义。第二步是向求解器配置添加停止条件，条件必须是评估为true或false的语句。

在瞬态求解器中使用停止条件

为了演示如何设置停止条件，我们来看一个瞬态传热问题。当最高温度超过阈值时，设置停止计算（我们也可以使用不同的条件，但是过程是一样的）。

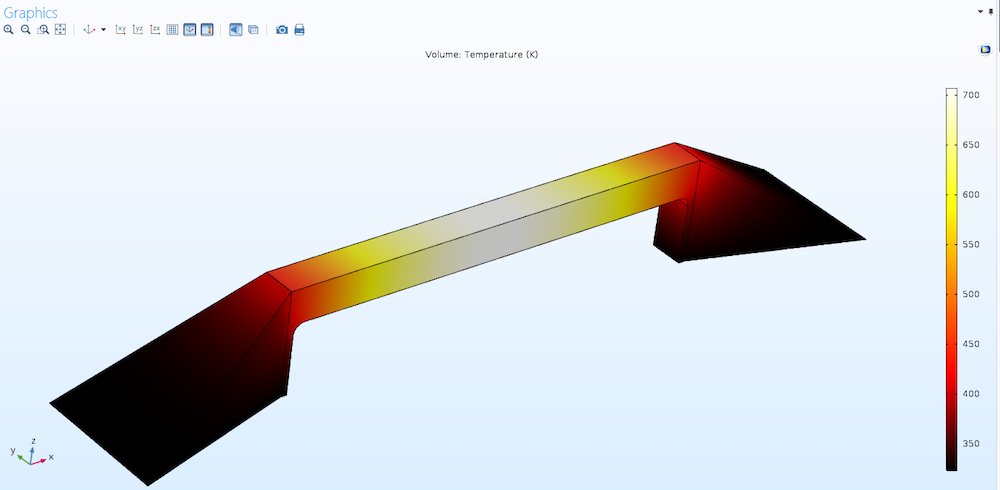
下图为一个由移动的热脉冲加热并通过辐射冷却到周围环境的硅晶片模型。（有关更多详细信息，请查看 COMSOL 案例库中的教程模型:硅晶片激光加热）我们希望通过修正模型，在达到阈值温度时停止计算。

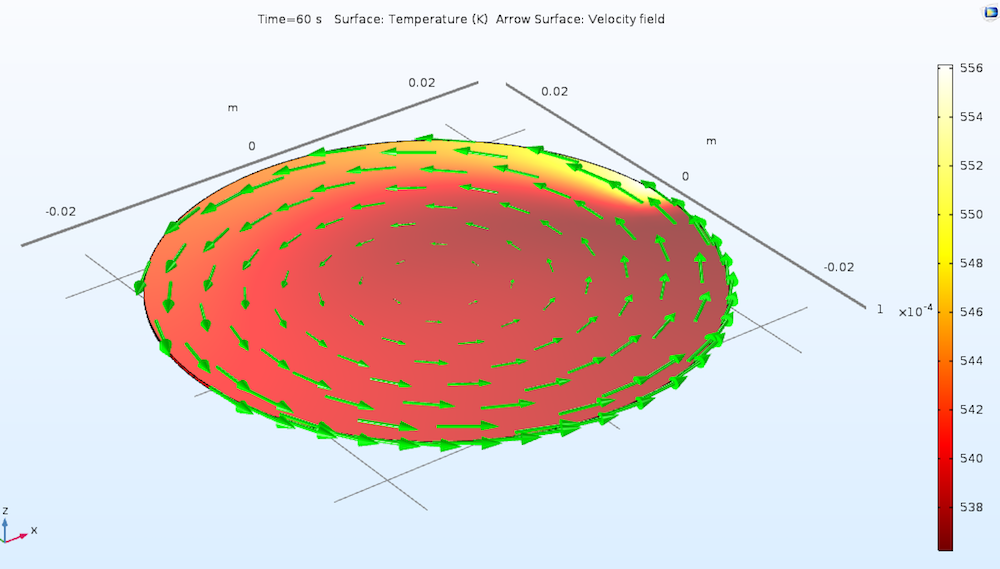
通过移动的热脉冲加热的旋转晶片上的温度分布。

首先，我们在几何实体上通过求积分值、平均值、最大值或最小值定义一个标量。如果我们对某一特定点感兴趣，可以使用点探针或积分组件耦合。在此示例中，我们监控的标量是最高温度，可以使用最大组件耦合算子来获得。

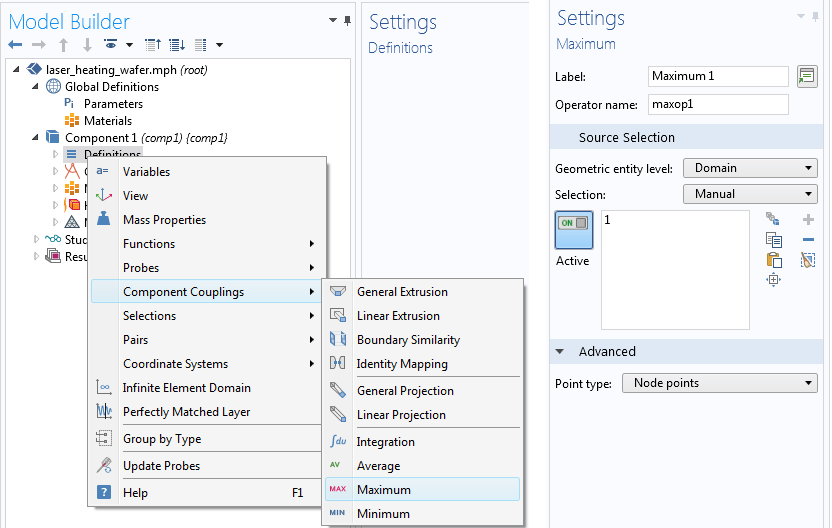
添加最大组件耦合算子的步骤。

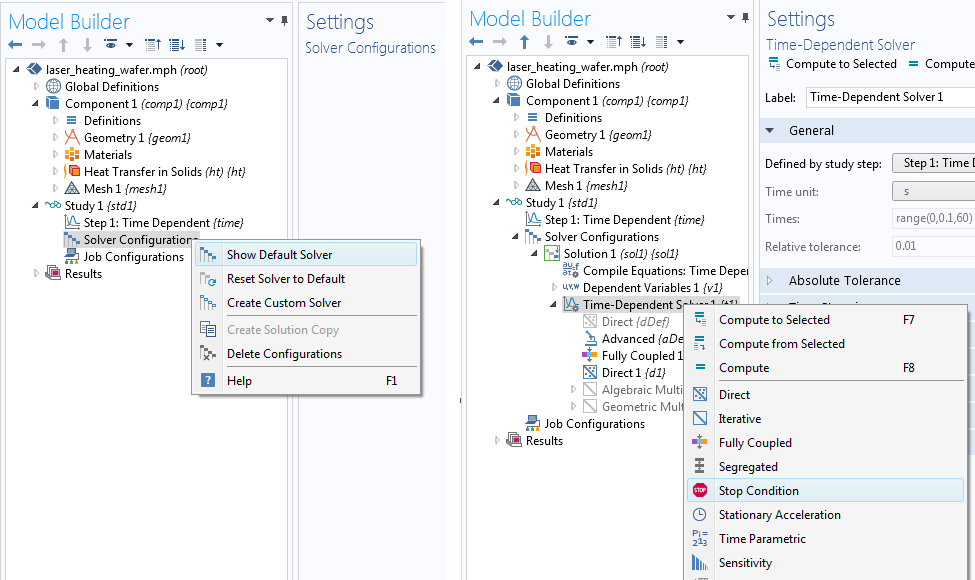
首次计算研究时，我们使用显示默认求解器 命令打开设置。然后，可以转到求解器配置 下的瞬态求解器 节点并添加停止条件 节点。

在求解器配置中，瞬态求解器节点可添加停止条件节点。

最后一步是在停止条件 设置窗口中添加表达式和条件。

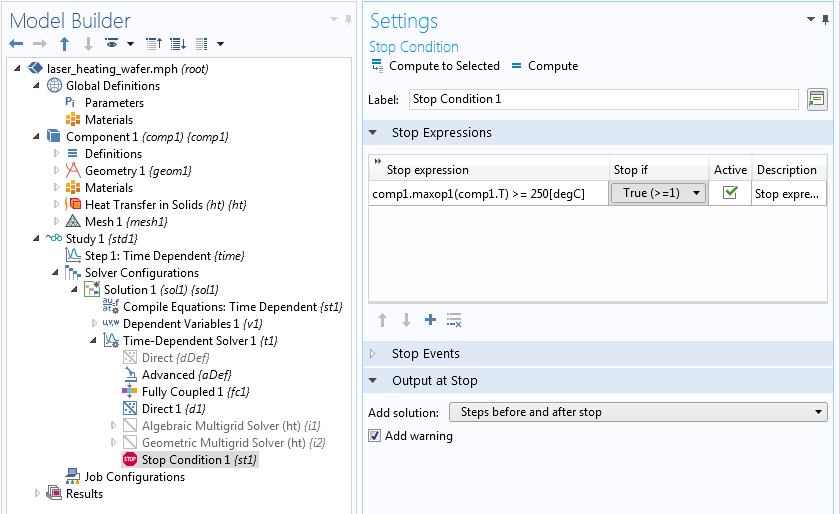
瞬态求解器的“停止条件设置”窗口。

当最高温度大于或等于 250°C 时，上述停止条件将停止求解器。因为满足了停止条件，所以求解器在 27.238 秒后停止（即使我们要求它在研究设置中计算 60 秒）。我们可以在求解器序列中添加的警告节点中看到截止时间。

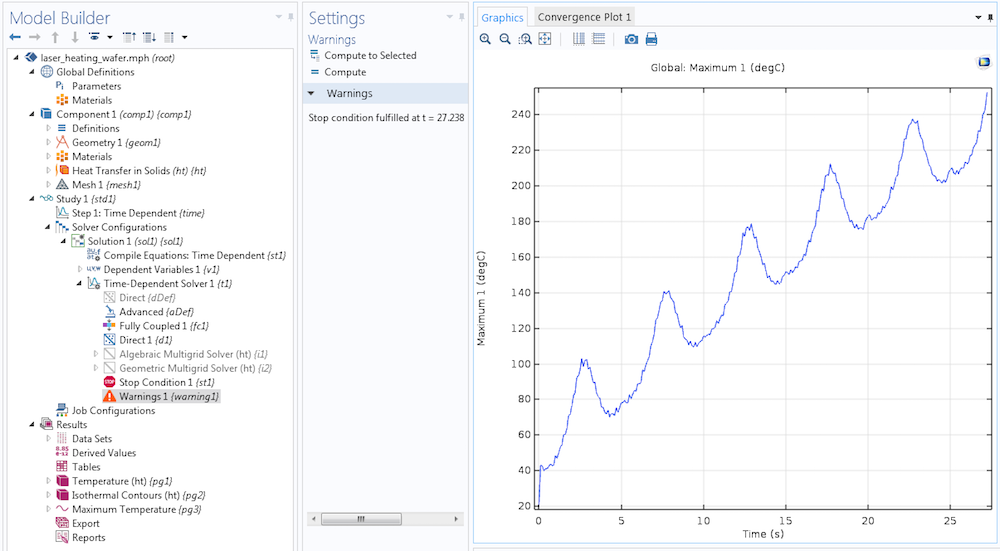
默认情况下，如果计算因停止条件而终止，则求解器会添加一个 警告节点。

在停止条件设置窗口中，我们使用 COMP1 名称范围，以确定最大的算子和温度变量 T。这些是在组件1 下定义的项目，而求解器序列是全局项目。例如，如果我们的模型中有第二个组件并重新定义了 maxop1，则求解器序列无法确定我们所指的是哪个运算符。因此，我们必须使用组件标识符。

请注意，当条件为真或假时，我们可以选择是否要停止。此外，在停止时输出部分，我们可以决定是否要在满足停止条件之前或之后添加时间步骤。

如果模型开发器中有事件接口，则可以通过在停止条件设置窗口中的停止事件 下添加以将其用作停止条件。

当时间步太小时停止

COMSOL Multiphysics 中瞬态求解器是自适应的。因此，时间步长的选择可基于用户指定的误差容限和计算出的局部误差估计值。当误差估计很高时，该软件将采取越来越小的步长。例如，当解奇异时，就会发生这种情况。如果我们想在时间步长太小时停止求解，而不是试图用越来越小的时间步长来求解奇异点，则可以通过保留变量 时间步长 来添加停止条件。

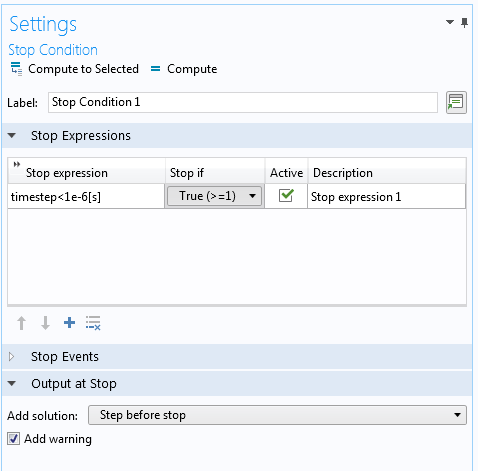
由于 timestep 是一个预定义的全局参数，因此无需名称范围即可识别它。

参数化求解器中的停止条件

停止条件还可以添加到频域研究以及参数化稳态研究中。参数化稳态研究可以是常规参数化扫描或辅助扫描。在所有这些情况下，应将停止条件 节点添加到求解器配置 > 稳态求解器 下的参数节点。

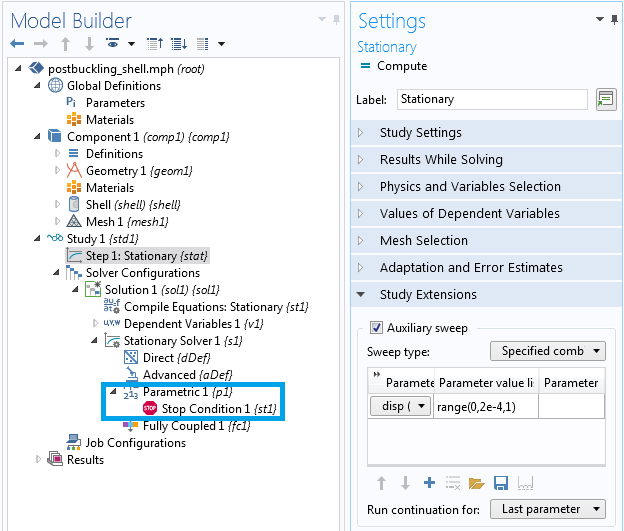
在执行辅助或参数化扫描时，可以在稳态分析中添加停止条件。

注意，与瞬态问题一样，我们需要一个标量变量进行监视，并且必须在停止条件下使用正确的变量范围。

如果你想查看如何在辅助扫描中使用停止条件来执行非标准载荷斜升过程，请查看壳结构的后屈曲分析案例模型。

变量、函数和组件耦合命名空间

停止条件中使用的表达式以及求解器配置中的其他项目必须是全局的才能自动识别。否则，我们必须提供组件名称作为前缀。组件内部的每个变量（包括温度等物理变量，如 T）和函数都是如此。另一方面，在模型开发器中的全局定义 下定义的 参数将被识别而无需组件前缀。

例如，当提到内置的积分算子时，我们可以简单地使用积分。与此相反，当涉及到在组件 comp1 中定义的积分算子 myint 时，我们必须使用 comp1.myint。

下述预定义的常量、变量、函数和运算符可以在求解器配置中使用，而无需标识组件：

物理常数，例如重力加速度 g_const
数学常数，例如 pi
内置全局变量，例如 t 表示时间，freq 表示频率
内置数学函数，例如三角函数和指数函数
内置算子，例如微分和积分算子

有关完整的列表和语法，请参见《COMSOL 参考手册》。

在本篇博客文章中，我们讨论了当满足一个或多个条件时，如何添加条件以停止瞬态或参数化求解器。如果您对此主题或 COMSOL Multiphysics 的使用有任何疑问，请点击下方按钮与我们联系。

联系 COMSOL

利用最大值原理节省计算时间和资源

Tue, 09 May 2017 06:37:02 +0000

当你的仿真计算量很大时，你会购买内存更大的计算机吗？如果求解耗时较长时，你会通宵运行它们吗？很多时候，你没有其他选择。但如果你有合适的工具，就可以通过利用数学原理找到更好的方法。今天，我们将展示如何在 COMSOL Multiphysics^® 软件中使用 最大值原理 节省计算资源和时间。

最大值原理简介

我们经常想知道某些量的最大值或最小值。当自由度数很大时，寻找极值的计算成本可能很高。如果使用极值作为输入，例如在边界条件或材料属性中，计算成本会更高。控制器设计就是这样一个例子。

假设我们事先掌握可能的关键位置的信息，那么，我们可以将搜索重点集中在这些位置。在瞬态问题中，如果可以仅存储可疑区域的数据，就可以节省内存。

挑战在于，对于许多问题，我们没有这样的信息。但是对于一些问题，我们可以证明极值出现在边界上。在数学中，这种性质被称为最大值原理。

COMSOL Multiphysics 提供了仅在边界上查找极值的方法，并允许我们将解存储在有限的一组域或边界上。

今天，我们将向您展示如何利用最大值原理高效求解和后处理。首先，我们将讨论最大值原理存在的条件，并简要叙述其数学证明。接下来，我们将演示 COMSOL Multiphysics 提供的使用这些原理的方法，包括边界上的最大值和最小值运算符、在表面上定义的物理场接口，以及边界元方法等。最后，我们将重点讨论最大值原理不成立的常见情况。

在开始之前，请注意，虽然最大值原理是有用的，但我们只应该在前提有效的情况下应用它们。否则，我们将会被路灯效应引入歧途。

当你找不到某些东西时，就会发生路灯效果，因为你只在容易查找的地方搜索。它来自一个著名的笑话，讲一个人在路灯下寻找他的钱包，即使他知道他把它留在了附近的公园里。

推导最大值原理

让我们从一个简单的一维问题开始。在一段区间范围内，考虑二阶常微分方程

\frac{d^2u}{dx^2}=0

该方程可以代表几个一维稳态边界值问题，例如在没有平流或源/汇的情况下的热传导或化学输运。不论物理性质如何，其一般解都是一条直线

u(x) = ax+b,

其中，常数 A 和 B 可以根据边界条件确定。

由于解是一条直线，它的最大值和最小值将位于域（区间）的左端或右端。因此，如果我们对极值感兴趣，只需要检查左右两端的值。如果两个边界条件都是狄利克雷类型，指定 u，我们甚至不需要求解方程来找到它的最大值和最小值。狄利克雷边界条件中较小的值为最小值，较大的值是最大值。这显然为我们节省了一些时间。

具有均匀、各向同性性质的对流扩散问题

在上面的分析中，我们利用对解的一般形式的知识得出有关极值位置的结论。对于更复杂的源项或高于一维的空间维度，这并不是一种实用的方法。与其推导出解的一般形式，不如使用初等微积分中的局部极大值或极小值的性质对以下线性偏微分方程做出类似的结论。

-\kappa\Delta u + \mathbf{v}\cdot \nabla u = f, \quad f<0, \textrm{ 在 } \Omega \textrm{中}

其中，是拉普拉斯算子；是梯度算子；k 是正标量（扩散系数或传导系数）；v 是对流速度;f 是源项。请注意，源项在域中的所有位置都是负数。

解在域的内部点能否达到最大值？从多变量函数的最优条件中，我们知道如果一个函数是平滑的，那么梯度在临界点应该为零。此外，在局部最大值处，所有二阶偏导数都应为负数或零。这两个条件导致偏微分方程的左侧为正或零。

在内部局部最大值处，

-\kappa\Delta u + \mathbf{v}\cdot \nabla u \ge 0

这与源项相矛盾。在同一等式的右侧，

f<0

这意味着我们的解的最大值只能在边界上找到。我们刚才证明的被称为强最大值原理。

还有弱最大值 原理，当允许源项为零时，该原理成立；即，是条件。在这种情况下，最大值要么出现在边界处，要么解始终是恒定的。无论哪种方式，如果要寻找最大值，只需寻找边界就足够了。我们在这里跳过弱最大值原理的证明。当，我们可以推导出最小值的类似原理。

最后，如果没有源或汇，我们可以结合弱最大值和最小值原理，得出解的最大和最小值都应该在边界上的结论。习惯上，我们使用最大值原理一词来指代最大值原理和最小值原理，具体指代哪个应结合上下文理解。

请注意，我们需要解具有平滑度才能得出上述结论。

各向异性，非均质相对流扩散问题

到目前为止，我们的结论可用于稳态对流扩散型物理问题，如传热、电流或化学传输，前提是电导率（扩散率）是均匀的和各向同性的，并且对流速度 v 也是均匀的。现在让我们取消这些限制。

通常，稳态对流扩散问题的形式为

\nabla \cdot (-\mathcal{D} \nabla u + \mathbf{v}u) = f,

其中，D 是电导率（扩散）张量，可以是各向异性和异构性的；v 是潜在的不均匀对流速度;f是热（化学/电流）源。

建立平滑解的弱最大值原理的要求如下：

扩散张量 D 是正定的
对流速度 v 是无发散的；即
源项为非正数；即

从物理上讲，这涵盖了不可压缩对流速度的传输问题，例如传热、反应流和电荷传输问题。无论如何，如果，可以得出最小值应该在边界上的结论。

考虑电加热器、保险丝和其他导体中的焦耳加热问题(详见这个视频)，其中电气部件中的电阻损耗会导致加热。固体传热方程由下式给出

\nabla \cdot (-\mathcal{\kappa} \nabla T ) = \sigma|\nabla V|^2,

其中，k 和 σ 是热导率和电导率，T 和 V 是温度和电势。

源项始终为非负数。根据我们到目前为止的讨论，可以得出结论，最低温度必须在模型的边界上。请参阅下图，其中标注了体积和表面最小值的位置。这两个位置重叠。

焦耳热问题中的温度分布(左)、最低总温度的位置(中心)和最低边界温度的位置(右)。

瞬态问题

瞬态问题大致可分为抛物线问题和双曲线问题。第一组包含扩散型现象，例如传热，化学反应和地下水流。第二组包含波型问题，如声学、电磁波和结构动力学。

对于抛物线问题，我们可以证明解的总体最大值或最小值是在初始时间或边界处遇到的。与稳态问题一样，源项的符号在这里起着决定性的作用。双曲线问题通常不遵循最大值/最小值原理。

考虑以下具有适当的初始和边界条件的抛物线方程

\frac{\partial u}{\partial t}+\nabla \cdot (-\mathcal{D} \nabla u +\mathbf{v}u) = f

如果扩散张量 D 是正定的，那么对流速度 v 是无发散的，源项。可以证明解在所有时间和点的整体最大值（而非任意给定时刻的最大值）要么出现在边界处，要么在初始时刻出现。

为了简化这里的讨论，让我们考虑上述抛物线方程的一维版本的强最大值原理。

\frac{\partial u}{\partial t}+\frac{\partial}{\partial x}(-D \frac{\partial u}{\partial x} +vu) = f, \quad x \in [0,L], \quad t\in[0,T], u(x,0) = u_0(x)

用导数的乘积法则扩展此等式，得到

\frac{\partial u}{\partial t}-\frac{\partial D}{\partial x}\frac{\partial u}{\partial x} -D \frac{\partial^2 u}{\partial x^2} +v\frac{\partial u}{\partial x}+u\frac{\partial v}{\partial x} = f, \quad x \in [0,L], \quad t\in[0,T], u(x,0) = u_0(x)

为了证明强极大值原理，我们将假设 u 的最大值位于时空域的内部点，并说明这一假设如何导致矛盾。

在内部最大值处，平滑解将具有。此外，对于一维问题，不可压缩的平流速度将处处都有。因此，在内部最大值下，上述等式简化为

– D \frac{\partial^2 u}{\partial x^2} = f

由于 D 为正，f 为负，这意味着在内部最大值，这与微积分的通常要求相矛盾，即在内部最大值时，。

这就使我们把时空域的边界作为最大解的可能位置。这个复合域的边界包括初始时间 t = 0、结束时间 t=T 以及 x=0 和 x=L 处的空间边界。

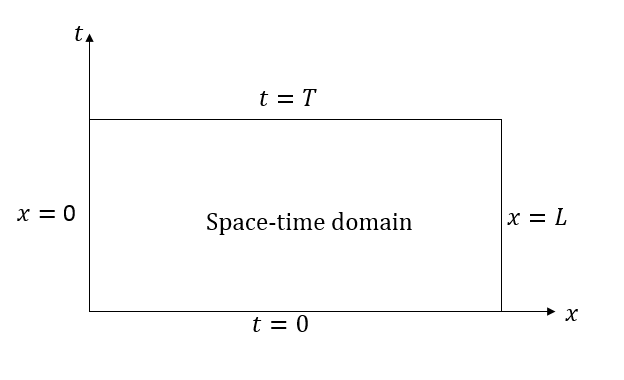
一维瞬态偏微分方程的时空域。

我们已经将最大解的位置限定在上图所示的四个边界之内。我们最初的观点是，最大解可能出现在空间边界或者初始条件所定义的时刻。这就排除了那些在空间内部但在终端时间 t=T 的点；也就是上述时域中矩形的顶部。我们来说明为什么会这样。

假设最大值位于时间边界 t=T 的一个空间内部点。如果我们从那个点向左或向右移动，即在空间中移动而不是在时间上移动，解不应该增加。因此，然而，第一个时间偏导数不必为零，因为我们只能从终端时间向一个方向移动。这里的限制是，要想在终端时间发生最大值，时间偏导数在那里不能为负。也就是说，我们需要。这与偏微分方程一致吗？将第一个空间导数设置为零，我们得到

\frac{\partial u}{\partial t}- D \frac{\partial^2 u}{\partial x^2} = f \Rightarrow \frac{\partial u}{\partial t}= f+D \frac{\partial^2 u}{\partial x^2}

由此，我们可以看到，关于源项的起始假设和对二空间偏导数的限制导致了一个负时间导数。这个基于偏微分方程的结论与我们根据局部最大值的要求所作的陈述相矛盾。相反，在初始时间使用类似的推理表明，在初始条件下可能的内部最大值处的时间导数是可能的。

在计算工作中，这意味着如果我们的目标是寻找最大的解，应该将搜索限制在边界内，但除了初始时刻，也应该考虑内部点。但是请注意，这种说法仅适用于所有时间和积分范围内的最大值。给定时间的最大值仍然可能在内部点。

系统和高阶方程

最大值原理通常不适用于高于 2 阶的方程，例如双谐波方程或二阶系统（例如二维和三维应力分析）。寻找最大值原理的基本思想是得到解向量 u 的一些标量函数 P（u）来满足泊松方程。这样的标量函数被称为 P 函数，以 L. E. Payne 的名字命名，他对这一思想做出了重大贡献。工程上的挑战是找到具有实际意义的 P 函数。

例如，考虑稳态应力分析。平衡方程由方程组给出

\sigma_{ij,j}+f_i = 0, i,j=1,2,3,

式中，σ_ij 和 f_i 分别是每单位质量的应力张量和体力的分量。

在线性弹性的情况下，应力和应变通过本构关系相关

\sigma_{ij}=\lambda \epsilon_{kk}\delta_{ij}+2\mu \epsilon_{ij}

其中，是应变张量的分量，且与位移 u_i 密切相关，这种关系通过应变-位移关系来定义

\qquad \epsilon_{ij}=\frac{1}{2}(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})

如果材料属性 λ 和 μ 是恒定的，并且体力 f 是螺线型的（无发散），例如非相对论应用中的引力情况，我们可以证明，体积变化，也称为膨胀，同时满足最大值和最小值原理。

我们可以通过代入平衡方程中的本构关系来证明这一点，得到

\lambda \epsilon_{kk,i}+2\mu\epsilon_{ij,j}=0, \quad i,j=1,2,3

并取上述向量方程的散度得到

\lambda \epsilon_{kk,ii}+2\mu\epsilon_{ij,ji}=0, \quad i,j=1,2,3.

从微分阶的应变-位移关系和微分次序互换性可以看出。这最终导致

\epsilon_{kk,ii}=\Delta \epsilon_{kk} = 0

由于膨胀满足拉普拉斯方程，因此其最大值和最小值都必须在边界处实现，除非膨胀在物体上是均匀的。对本构关系的追踪表明，在线性弹性、各向同性材料属性和无发散体积力假设下，平均应力也是如此。

虽然上述结果在理论上很有吸引力，但工程师很少对寻找膨胀或平均应力的极值感兴趣。另一方面，最大 von Mises 应力和最大剪切应力是重要的标量。例如，弹性极限（屈服标准）通常根据这两个量中的任何一个来确定。不幸的是，对于这些和其他实际利益量，我们没有广泛适用的最大值原则。但针对特殊情况仍然可以推导出相应的最大原则。

一个很好的例子是对扭转的均匀梁分析。如果我们选择 z 轴作为梁的轴，应力分析问题可以根据在横截面 Ω 上定义的应力函数重新表述。在没有体积力的情况下，应力函数满足

\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2} =-2, \quad (x,y) \in \Omega

应力的非零分量为

\sigma_{xz}=\mu\theta\frac{\partial \phi}{\partial y}, \quad \sigma_{yz}=-\mu\theta\frac{\partial \phi}{\partial x}

其中， θ 是梁每单位长度的扭转角度。

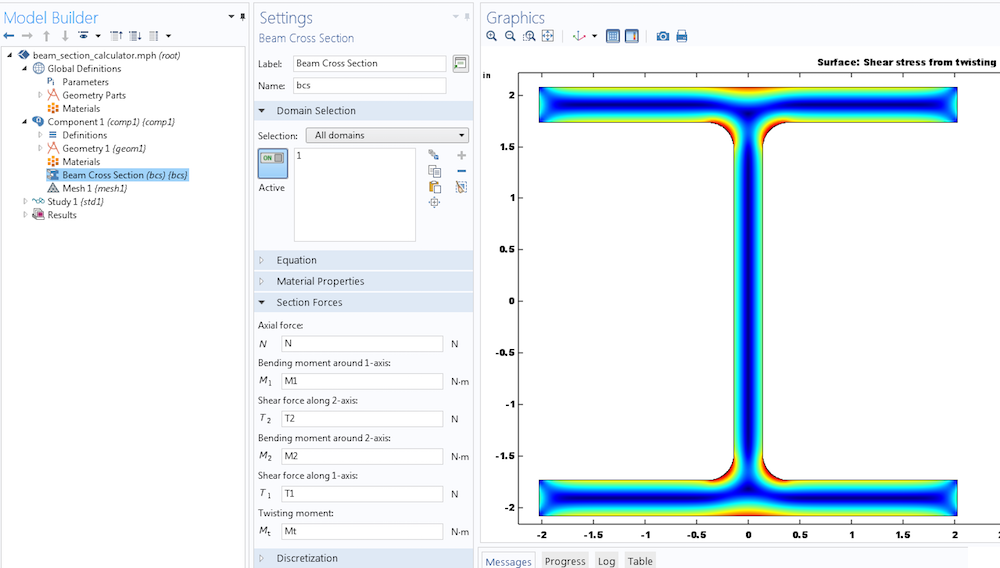
使用梁横截面接口计算的扭转应力分布。

我们对最大剪切应力感兴趣。请注意，由于扭转问题不存在法向应力，因此剪切应力的大小与 von Mises 应力成正比。对于剪切应力的大小 τ，我们有

\tau = \sqrt{\sigma_{xz}^2+\sigma_{yz}^2} \Rightarrow \tau^2= \sigma_{xz}^2+\sigma_{yz}^2=(\mu\theta)^2|\nabla\phi|^2

我们以的散度来研究最大值原理的可能性。使用指数表示法

div(|\nabla\phi|^2)=\frac{\partial^2}{\partial x_j\partial x_j}(\frac{\partial \phi}{\partial x_i}\frac{\partial \phi}{\partial x_i})=2\frac{\partial}{\partial x_j}(\frac{\partial \phi}{\partial x_i}\frac{\partial^2\phi}{\partial x_i\partial x_j})=2\frac{\partial^2\phi}{\partial x_i\partial x_j}\frac{\partial^2\phi}{\partial x_i\partial x_j}+2\frac{\partial\phi}{\partial x_i}\frac{\partial^3\phi}{\partial x_j\partial x_i\partial x_j}

如果我们交换上述等式最后一项中的微分顺序，可以得到

div(|\nabla\phi|^2)=2\frac{\partial^2\phi}{\partial x_i\partial x_j}\frac{\partial^2\phi}{\partial x_i\partial x_j}+2\frac{\partial\phi}{\partial x_i}\frac{\partial}{\partial x_i}(\frac{\partial^2\phi}{\partial x_j\partial x_j})

括号中的项是应力函数的散度。根据我们最初使用的等式，这个值是 -2。因此，上面的第二个右手项为零。第一个右手项是非负的，因为它是的 Hessian（二阶偏导数矩阵）的分量的平方和。此外，它不能为零，因为 Hessian 的对角线加起来是一个非零值 -2。

因此，我们有

div(\tau^2)>0 \quad \forall (x,y) \in \Omega

这意味着剪切应力的大小在梁横截面的边界处达到最大值。许多关于线弹性的教科书都包含了针对简单横截面和边界条件的 Saint-Venant 扭转问题的解析解。这些显式解表明，最大的剪切应力出现在边界处。我们在这里所做的是针对任意横截面和边界条件得出这一结论，而没有明确解决边界值问题。请参阅下面承受扭转的工字梁的比较。

比较扭转作用下梁中整体最大剪应力(左)和边界最大剪应力(右)的位置。

如何利用 COMSOL Multiphysics^® 软件中的最大值原理

假设感兴趣的物理量存在最大值原理，或者你只想关注边界处的物理量，那么你可能就只对在问题边界上的极值感兴趣。COMSOL Multiphysics 有哪些功能可以帮助你做到这一点呢？

后处理阶段的最大值和最小值计算

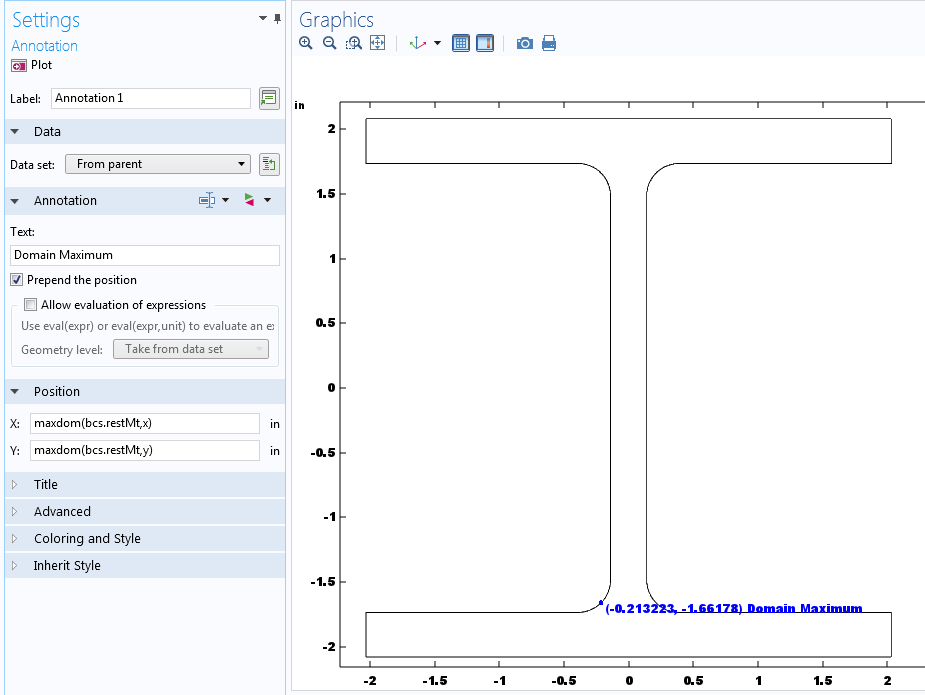
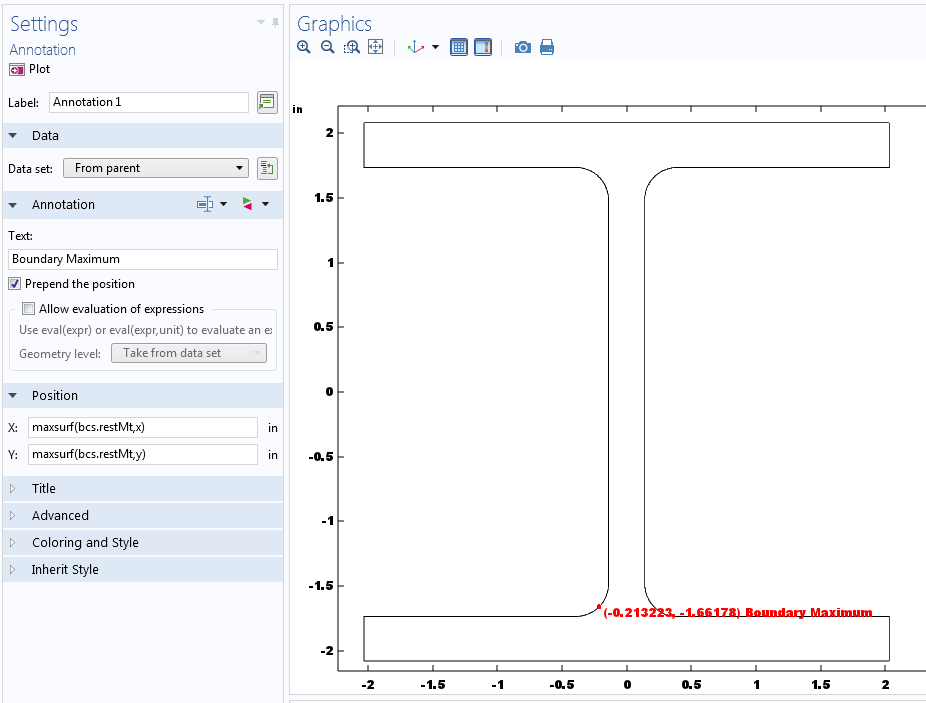
如果从模型生成器或 GUI 的菜单中进入结果 > 派生值，就会找到在体积、面或直线上定义的最大值和最小值运算符。当你对边界上的极值感兴趣时，可以使用如下所示的表面或线算子，具体取决于问题的空间维度。

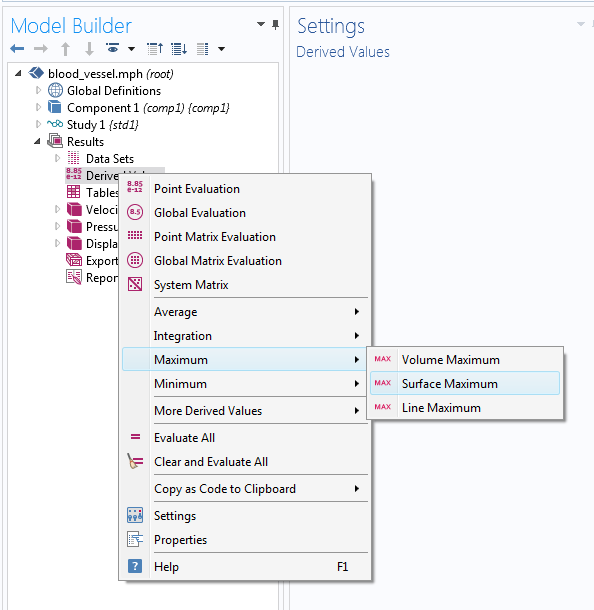
可以在不同的几何实体级别上完成最大值和最小值计算。

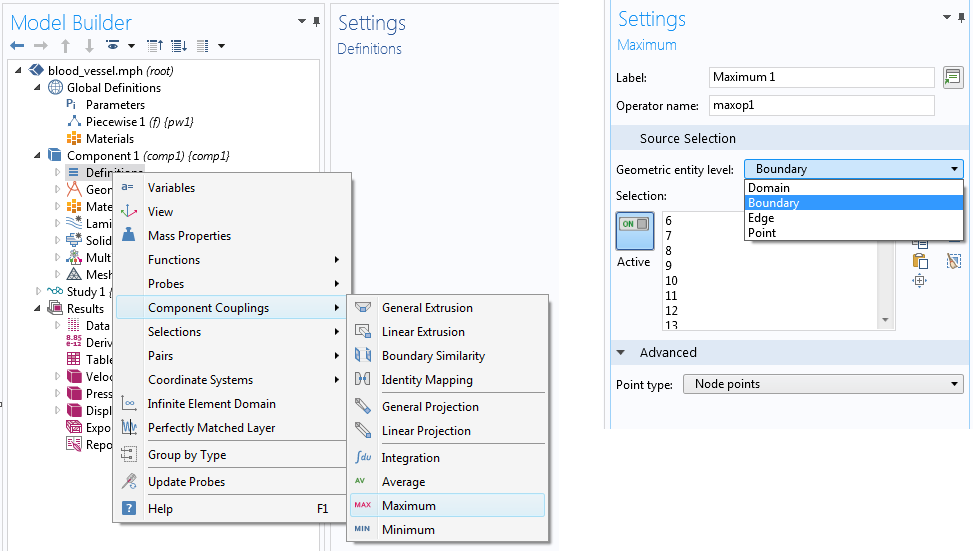
最大值和最小值组件耦合算子

上述算子的使用仅限于后处理。如果你必须在物理场中使用极值，例如实现控制器，则可以在模型的定义部分中定义最大值或最小值组件耦合算子。这些运算符还允许在体积、面、曲线或点之间选择几何实体。添加算子后，在设置窗口中选择几何实体级别，如下所示。

组件耦合运算符的几何实体选择。

除了由于自由度较低而节省时间和内存外，边界耦合运算符对所涉及的矩阵结构造成的干扰也比域耦合运算符小。如果你知道要求解的方程具有最大值或最小值原理，并且需要在问题表述中使用极值，那么 COMSOL Multiphysics 提供了一种经济的替代方案，即使用边界耦合算子而不是域耦合算子。

将解存储在几何体的选定零件上

在一个瞬态的问题中，你只对边界数据的后处理感兴趣，当模型较大且存在内存限制时，只存储几何体的关键部分的解可能是一种既经济又必要的方法。我们在之前的博客中讨论过，在 COMSOL Multiphysics 中，有不止一种方法可以做到这一点，。

表面疲劳

如果你正在进行疲劳分析，并且知道临界行为位于几何体的边界处，COMSOL Multiphysics 将为你提供仅限于边界的疲劳分析功能。

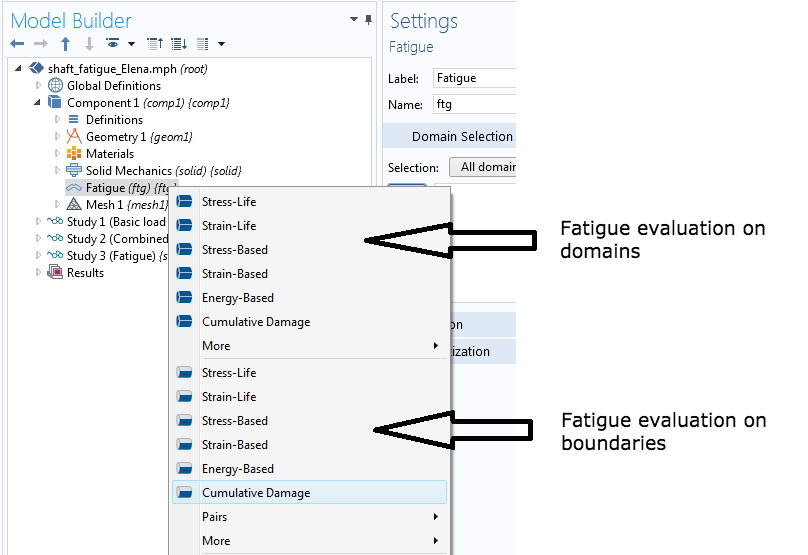
域与边界的疲劳分析。

边界元法

COMSOL Multiphysics 主要基于有限元方法。对于某些问题，它支持边界元方法。在最新版本的软件(5.3 版)中，边界元方法可用于静电、腐蚀和用户定义的方程。

边界元方法解决的问题通常不含源项，因此很可能同时满足最大值和最小值原理。不过，利用最大值原理并非选择边界元方法的充分理由。但当采用边界元方法时，问题在边界上极可能存在极值。

注意事项

最大值原理在应用于其前提适用的问题时非常有用。然而，我们应该避免将其应用于这些前提条件不适用的问题。例如，源项符号的不连续性和变化就不复合这些前提。

不连续性

在我们的数学分析中，我们假设系数的平滑度。如果存在不连续性，则这些原则不适用于整个域。然而，我们可以将域细分为若干连续的区域，并在每个子域上应用最大值原理。实际上，这意味着你必须包括内部边界和外部边界。具有不同材料属性的两种材料之间的界面就是一个例子。

我们之前提到过，在 COMSOL Multiphysics 中，疲劳分析可以在域或面上进行。在许多问题中，疲劳失效始于表面。但是在接触力学中，已知疲劳失效始于次表面点。有关这方面的更多信息，包括有限元网格划分策略的含义，请参阅以下有关接触疲劳建模的博客文章。

更改源项的符号

在非零源项的问题上，最大值原理要求源项具有非负性或非正性。因此，如果源项在域内改变符号，最大值原理将不再适用。例如，在焦耳热问题中，电磁热源始终为正。另一方面，在化学反应中，相同的化学物质在域的一部分区域产生，而在其他区域消耗。除非我们确定反应在整个域内都是单一地产生或消耗某种化学物质，否则不应使用最大值原理。

离散化的影响

我们对最大值原理的推导直接使用偏微分方程。离散化过程可能会破坏这一原理的适用性。因此，当发现某个理论上应遵循最大值原理的问题在数值求解中未能体现时，我们应检查所使用的数值方法是否遵循离散最大值原理。此外，还需仔细检查是否存在数值误差。

关于使用最大值原理的结论性思考

最大值原理在偏微分方程的分析中占据重要地位，常用于证明解的存在性与唯一性、确定误差界限以及实现其他类似目标。在这篇博客中，我们展示了如何利用这些原理进行高效的计算分析。

请注意，本文第一部分中提供的数学讨论针对更广泛的受众。有关更严格的讨论，请参阅偏微分方程分析中的标准文本。以下是我个人推荐的有关这个主题的一些参考：

Lawrence C. Evans, Partial Differential Equations, American Mathematical Society, 2010
Rene Sperb, Maximum Principles and Their Applications, Academic Press, Inc., 1981

如果你对本主题或使用 COMSOL Multiphysics 有任何疑问，请联系我们。

联系我们

变化极限的积分和求解积分微分方程

Thu, 06 Oct 2016 07:38:08 +0000

在上一篇博客中，我们讨论了时间和空间的积分方法，了解了如何使用积分耦合算子计算反导数。今天，我们将进一步扩展这个想法，介绍如何分析变化极限的空间积分，无论它们是显式指定还是隐式定义。这个技术对分析结果以及在 COMSOL Multiphysics^® 软件中求解积分和微分方程都有帮助。

积分的变化极限

在 COMSOL Multiphysics 中，我们可以通过使用积分组件耦合算子或结果部分派生值 下的积分工具来计算空间积分。虽然这些积分总是在一个固定的区域内进行计算，但有时我们会想改变积分的极限，并获得与新极限有关的结果。

例如，在一个一维问题中，积分算子通常会作如下计算：

I = \int_a^b f(x)dx.

其中，a 和 b 是域中的两个端点，代表积分上下限。

不过，我们要做的是，计算出：

I(s) = \int_a^sf(x)dx, \qquad s\in [a,b],

并得到关于积分 s 的可变极限的结果。

由于积分算子在一个固定的域内工作，我们来考虑如何使用它们来获得变化极限的积分。一个小窍门就是通过与一个在积分极限内等于1、在极限外等于0的函数相乘来改变积分值。也就是说，定义一个核函数

k(s,x) =
\begin{cases}
1 \quad x \leq s\\
0 \quad \mathrm{otherwise},
\end{cases}

并计算

I(s) = \int_a^Lk(s,x)f(x)dx = \int_a^sf(x)dx.

就像我们在上一篇关于时间和空间的积分方法的博客中所指出的，我们可以通过使用逻辑表达式或阶跃函数来建立这个核函数。

我们还需要知道在 COMSOL Multiphysics 中是如何指定辅助变量 s 的。这就是 dest 算子发挥作用的地方。dest 算子强制其参数在目的点上而不是在源点上被计算。在这个例子中，如果我们在 COMSOL 软件中把上述方程的左边定义为一个变量，那么我们就在右边输入 dest(x) 而不是 s。

我们用一个例子来证明这一点。例如，一个模拟了一个平行板反应器中的稳态放热反应的模型。在中心附近有一个加热筒，左边有一个入口，在 x = 0 处。其中一个化合物的浓度为 cA。

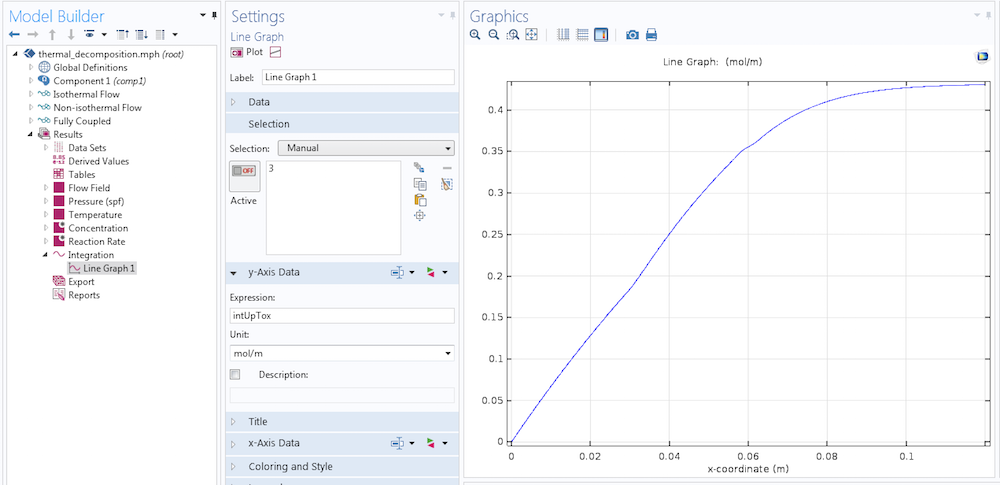
我们要做的是计算进气口和与进气口距离为 s 的横截面之间每单位厚度的总摩尔数。然后，将结果与进气口的距离作对比。

首先，我们为整个域定义一个积分耦合算子，保留默认的积分算子名称为 intop1。如果我们评估 intop1(cA)，就可以得到整个域的积分。为了水平地改变积分的极限，我们用一个阶跃函数建立一个核，我们把它称作step1。然后，我们定义一个新的变量，intUpTox。

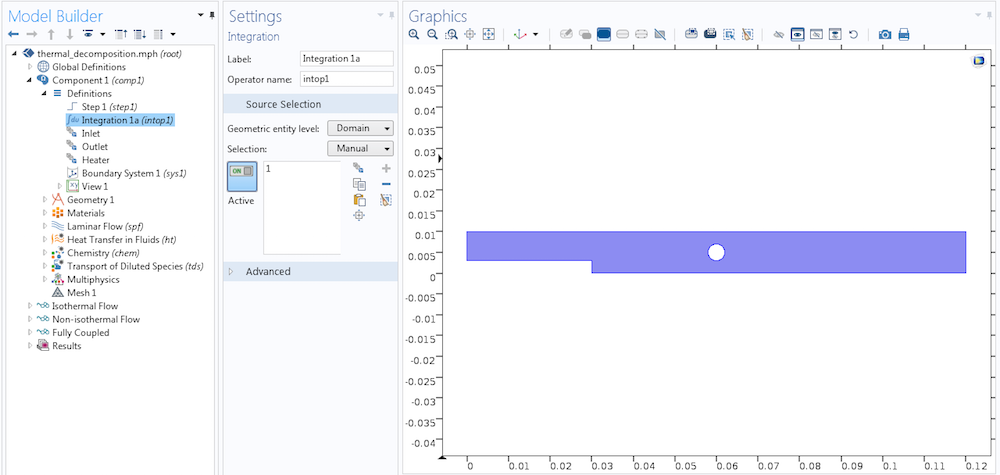
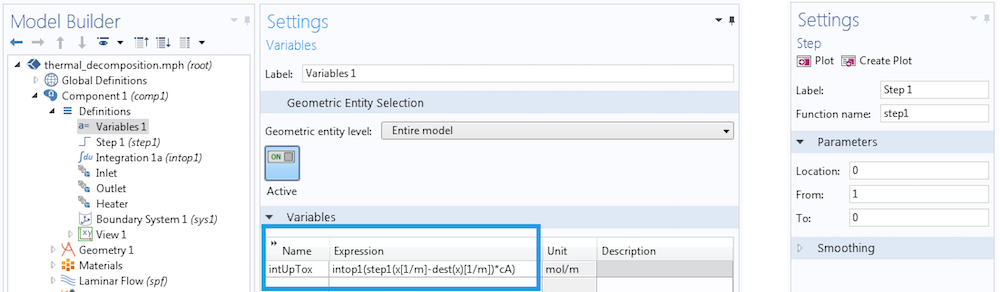
结合积分耦合算子、dest 算子和新变量来计算具有变化极限的积分。

我们来看看上图中描述的变量是如何工作的。作为一个变量，它是一个分布式的量，其值等于积分算子返回的值。在积分过程中，我们在积分域的每一个点上计算 x，只在计算 intUpTox 的点上计算 dest(x)。我们找到一条水平线，从入口处一直延伸到出口处，并绘制 intUpTox。

将浓度 cA 在一个积分域沿水平变化的极限上进行积分。

I(s) = \underbrace{\int_0^s\int_{y_{min}}^{y_{max}}c_A(x,y)dydx=\int_{\Omega} K(s,x)c_A(x,y)d\Omega}_{\text{Mathematical Expression}}=\underbrace{\mathrm{intop1(step1(x-s)*cA)=intop1(step1(x-dest(x))*cA)}}_{\text{COMSOL Implementation}}

如果我们改成绘制 intUpTox/intop1(cA)*100，就会得到一个给定点左边的百分数质量与 x 坐标的关系图。

在上述积分中，积分的极限是以x坐标为单位明确给出的。但有时，极限可能只以隐式标准给出，而反转这种标准并获得显式极限可能并不直接。例如，假设我们想知道在离加热缸中心一定径向距离内的总摩尔的百分比。给定从缸中心(x_pos, y_pos)的距离 s，我们希望核函数在径向距离内等于1，在其外等于 0。要做到这一点，我们可以使用：

k(s,x,y) = \mathrm{step1}\left[(x-x_{pos})^2+(y-y_{pos})^2-s^2\right].

但我们如何指定 s 呢？再次使用 dest 算子，带入等式得到：

k(s,x,y) = \mathrm{step1}\left[(x-x_{pos})^2+(y-y_{pos})^2- (\mathrm{dest}(x)-x_{pos})^2-(\mathrm{dest}(y)-y_{pos})^2\right].

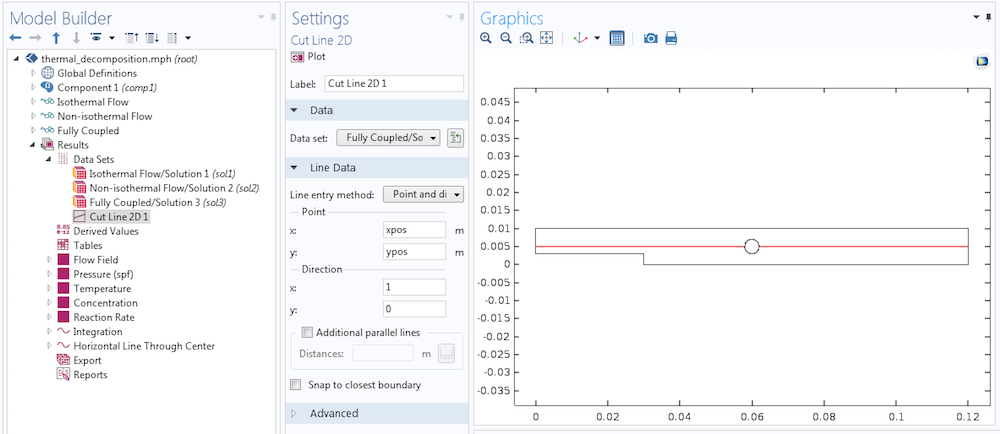
通过定义一个截线数据集来实现这个方法，用于获得通过孔中心的水平线，并将我们的积分表达式的图形置于其上。截线不一定是水平的，它只需要穿越积分算子定义的整个域。此外，s 应该在截线上单调地变化。

用穿过孔中心的截线制作的新数据集。

在下面的图片中，我们通过放大图表的左下角区域添加了一个函数这一部分显示，在距离加热孔中心不到 2 mm 的地方，绘图上没有结果。这是因为该区域不在我们的计算域内。由于孔的半径为 2 mm ，所以在 2 mm 的标点上，序数从 0 开始。

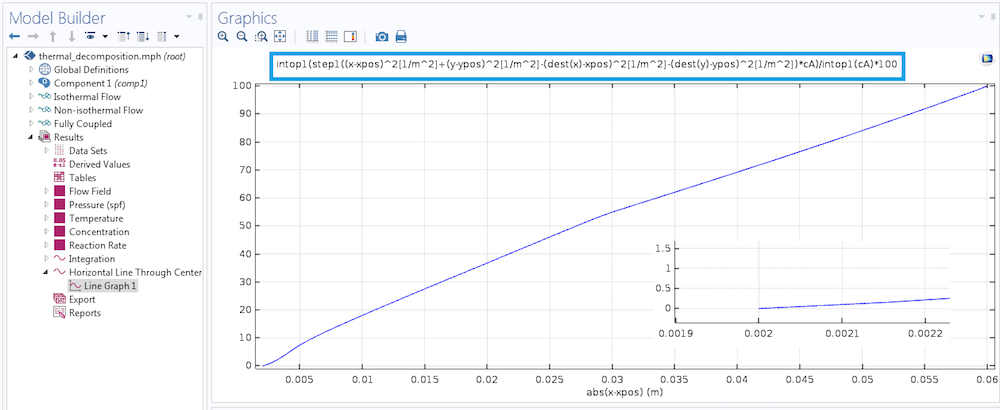
一个域中的质量百分比，在固定点的径向距离内。径向距离是通过使用隐式表达式中的dest算子来改变的。

积分和积分微分方程

在前面的小节中，我们在给出积分的情况下对积分进行了计算。但是，如果我们有了积分并想求解积分，该怎么处理？这种问题的一个例子是 Fredholm 第一类方程

g(s) = \int_a^b K(s,x)u(x)dx,

当给定函数 g 和核 K 时，我们要求解函数 u。这些类型的积分方程经常出现在反问题中。

在整数微分方程中，未知函数的积分和导数都会涉及。例如，假设我们有

\frac{du} {dx}+\int_a^bf(x,u(s))ds = g(x),

并且对于给定的所有其他函数，想要求解 u。

在 COMSOL 案例库中，有以下整数偏微分方程：

\rho C_p \frac{\partial T}{\partial t}+\frac{\partial }{\partial x}(-\kappa \frac{\partial T} {\partial x}) = \frac{4D_i} {D_o^2-D_i^2}\varepsilon \sigma T^4 – \frac{4}{D_o^2-D_i^2}\varepsilon \sigma\int_0^LK(x,s)T(s)^4ds,

其中，求解温度 T(x)，并给出所有其他函数和参数。

我们可以使用固体传热 接口来解决上述问题。在这个接口中，将上述方程的右侧添加为随温度变化的热源。第一个源项是可直接求解的，但我们需要使用积分耦合算子和 dest 算子在第二项中添加积分。对于名为 intop1 的积分算子，我们可以使用 intop1(k(dest(x),x)*T^4) 计算

\int_0^LK(x,s)T(s)^4ds

关于这个问题的实现和物理背景的更多细节，您可以点击这里下载整数-偏微分方程教程模型。请注意，一些积分方程往往是奇异的，我们需要使用正则化来获得解。

不同极限的空间积分总结

在今天的博客中，我们学会了如何在不同的空间极限上进行积分。这对于在后处理中计算积分或定义积分和微分方程是必要的。想要了解更多信息，请浏览以下 COMSOL 博客的相关内容。

关于积分和其算符的子完整列表，请参考 COMSOL 参考手册。

如果您对文中讨论的技术或对您的 COMSOL Multiphysics 模型有疑问，请随时与我们联系。

]]>

Temesgen Kindo – COMSOL 博客 -

非标准约束和弱贡献的力量

弱贡献简介

为极值问题添加约束

约束弹簧的平均垂直位移

替代实现方法

拉格朗日乘数的物理解释

关于弱贡献的总结性思考

下一步

图像去噪以及其他多维变分问题

高维空间中的变分问题

图像去噪：一个多维变分问题

高阶导数的变分问题

多未知数变分问题

结束语

查看更多关于“变分问题和约束”的系列博客文章

实现不等式约束的方法

用于路径规划的罚函数法

拉格朗日乘子法

有效集策略

松弛变量

增广拉格朗日方法

不规则形状的障碍物

下一步

查看更多关于变分问题和约束系列的博客文章

强制约束中数值问题的处理方法

对全局约束使用拉格朗日乘子法

罚方法

罚参数的辅助扫描

增广拉格朗日法

故意违反约束

后续操作

查看更多有关“变分问题和约束”问题的系列博客文章

在变分问题中指定边界条件和约束

约束分类

等式约束理论简介

在 COMSOL Multiphysics® 中施加约束

指定通量（力）

将约束添加到不在几何序列中的点

敬请关注！

查看“变分问题和约束”系列博客的更多博客文章

肥皂膜及其他变分问题建模概述

函数的最小值

求解变分问题

欧拉-拉格朗日方程

在 COMSOL Multiphysics® 中执行一个变分问题

指定一个更通用的符号形式

变分解与直接优化

后续操作

借助模型方法自动完成物理场选择和研究

自定义求解过程的优势

在 COMSOL Multiphysics® 中创建模型方法

利用模型方法自动完成弹塑性分析

结束语

更多相关资源

如何在 COMSOL Multiphysics® 中为求解器添加停止条件

停止条件：何时以及如何使用

在瞬态求解器中使用停止条件

当时间步太小时停止

参数化求解器中的停止条件

变量、函数和组件耦合命名空间

相关资源

利用最大值原理节省计算时间和资源

最大值原理简介

推导最大值原理

具有均匀、各向同性性质的对流扩散问题

各向异性，非均质相对流扩散问题

瞬态问题

系统和高阶方程

如何利用 COMSOL Multiphysics® 软件中的最大值原理

后处理阶段的最大值和最小值计算

最大值和最小值组件耦合算子

将解存储在几何体的选定零件上

表面疲劳

边界元法

注意事项

不连续性

更改源项的符号

离散化的影响

关于使用最大值原理的结论性思考

在 COMSOL Multiphysics^® 中施加约束

在 COMSOL Multiphysics^® 中执行一个变分问题

如何利用 COMSOL Multiphysics^® 软件中的最大值原理