由 Temesgen Kindo 创作的所有博客

利用最大值原理节省计算时间和资源
通过利用大型复杂模型中的最大值原理,你将节省时间和计算资源,而不必购买更大的计算机或让你需要一整夜来求解模型。
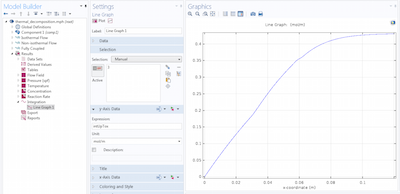
变化极限的积分和求解积分微分方程
学习如何分析变化极限的空间积分,无论它们是明确指定的还是隐式定义的。(第二部分,共2部分)

基于方程的轴对称组件建模指南
柱坐标系对于高效求解和后处理旋转对称问题而言很有用。COMSOL Multiphysics® 软件为轴对称物理场接口中的柱坐标系提供了内置支持。当您使用数学接口对定制的偏微分方程(partial differential equation,简称 PDE)进行定义时,请务必仔细辨明它们的意义。
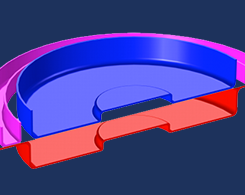
如何将变形形状作为几何输入重新使用
假设对一块金属(如一块薄板施)施加一定程度的机械载荷,金属将发生变形并呈现出一种与原始未变形构型不同的新形状。接下来,假设我们想将这个变形的形状作为一个新几何结构的一部分,然后在新复合域内求解其他物理场问题。今天,我们将为您演示如何将一个变形的对象作为几何序列的输入使用。
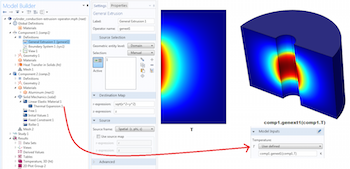
第 2 部分:用广义拉伸算子映射变量
在上一篇博客中,我们介绍了线性拉伸算子并演示了如何使用它们在源和目标之间映射变量。如前面所讲的,这种方法仅限于通过仿射变换将源和目标相关联的情况。今天,我们将讨论广义拉伸算子,旨在处理非线性映射和不同维度的几何实体之间的变量映射。 拉伸算子简要回顾 在目标实体中的一点处 Pd,我们希望计算一个量,该量是在源实体中定义的另一个量的函数。因此,来自源点 Ps 的量需要被复制到目标实体。拉伸算子用于识别源实体中的哪一点与目标实体中的某点相对应。换句话说,算子定义了点到点映射。 \textbf{T}:Pd \rightarrow Ps. 如果映射是仿射,知道源中的一些点如何对应于目标实体中的点就足够了。从这样的源-目标对中,可以从叠加推断出一般的映射。然而,一般来说,我们需要为映射编写数学表达式。这个表达式可以是源点 Ps 作为 Pd 的函数的显式定义,或者是 Pd 和 Ps 之间的隐式关系。 在 COMSOL Multiphysics 中使用广义拉伸算子 当使用 线性拉伸算子 时,我们直观地指出了足够多的点(基)的映射,COMSOL Multiphysics 计算出了如何转换剩余的点。使用广义拉伸算子 时,我们写出了目标域中任意点映射的数学描述。 首先,我们来重点讨论如何使用广义拉伸算子复制线性拉伸算子。然后,我们可以考虑必须使用一般拉伸算子的示例。 对于仿射关系,广义拉伸算子可以用作线性拉伸算子的替代。当涉及到一般的非线性映射时,广义拉伸算子是必要的。要添加广义拉伸算子,请点击 定义 > 非局部耦合 > 广义拉伸算子。 示例1 在关于线性拉伸算子的博客文章中,我们考虑了一个放射,它将源域中的点 1、4 和 2 与目标域中的点 1、5 和 3 配对。请看下面的图,几何图形中的两个圆的圆心在原点,半径分别为 1.0 和 1.5。 任何仿射变换都可以表示为线性变换和平移运算的和。因此,我们有 xs = axd + byd + e, \qquad ys = cxd + dyd + f. 现在我们需要找到常数 a,b,c,d,e, 和 f。由于源点(0,0),(1.0, 0)和(0,1.0) 分别对应于目标点(0,0) ,(1.5, 0)和(0,1.5),我们得到 xs = \frac{2}{3}xd, ys = \frac{2}{3}yd. […]

使用线性拉伸算子访问非局部变量
在许多仿真任务中,需要将变量从计算域的一个区域(源)转移到另一个域或组件(目标)。在 COMSOL Multiphysics 中,这种功能是通过定义一个点对点映射(即 拉伸算子),将一组目标点与一组源点相关联来实现的。一旦拉伸算子建立了映射,就可以使用相同的算子从目标访问在源处定义的所有变量。 在域之间映射变量 在许多实际情况中,需要将变量从一个组件或组件的一部分映射到另一个部分。两个子模型的连接就是这样一个实例,例如为湍流模型生成入口边界条件。入口处的边界条件明显影响域内的流体流动。然而,入口处的流动轮廓不像层流那样容易定义。为了产生湍流入口边界条件,可以使用法向流入的辅助模型。然后,需要将出口处的最终速度分布复制到主模型的入口。 效率可能是在域之间映射变量的另一个原因。例如,具有轴对称热边界条件和材料特性的热膨胀。如果结构边界条件不是轴对称的,我们可以通过先执行轴对称热分析,然后将温度从 2D 轴对称域映射到 3D 域进行结构分析以节省时间。 另一种常见的情况是周期性或其他边界条件的实现,其中边界上某个点的量与另一边界上某个点的量相关。例如,在二极管中,p-n 结一端的法向电流密度取决于同一点的电势和结另一端的电势。虽然在 COMSOL Multiphysics 的适当的物理接口中内置了大量这样的边界条件,但是用户有时可能会需要构建自己的边界条件。 以上这些情况都需要将变量从一个域或边界逐点映射到另一个域或边界。今天,我们为您展示将如何构建这些映射。 源和目标之间的映射 映射的思想涉及两个几何实体: 已知变量的源和将使用这些变量的目标。已知在源处的一个量,我们想计算目标域的另一个量。新的量可以与相同,或者是它的一个函数。 我们可以把这个问题分成以下几个步骤: 对于点 xd,想要评估 qd。 识别对应于点 xd 的源点 xs,此坐标变换由下式给出:xs = T(xd)。 提取 qs = qs(xs)。 建立关于变量 qs 的函数:f:qs\rightarrow qd 来计算 qd。 然后得到 qd(xd) = f(qs(T(xd))) 所以,本文的重点是转换 T : xd \rightarrow x_s。 COMSOL Multiphysics 提供了两种耦合算子来指定这种映射: 线性拉伸算子 和广义拉伸算子。线性拉伸算子更容易构建,但它们的用途仅限于仿射变换。广义拉伸算子更通用,但需要更多的精力进行定义。 这里,我们将讨论线性拉伸算子。在下一篇博文中,我们将讨论广义拉伸算子。 在 COMSOL Multiphysics 中使用线性拉伸算子 当源点和目标点通过仿射变换(如平移、缩放、反射、旋转或剪切)相互关联时,COMSOL Multiphysics 提供了一种指定拉伸算子的简单方法:线性拉伸算子。要添加线性拉伸算子,我们可以选择:定义 > 非局部耦合 > 线性拉伸。 线性拉伸算子的基本思想是:如果我们知道线上的两对对应点时,就可以定义两条线之间的仿射变换。类似地,三对非共线点和四对非平面(不超过两个共线)点分别描述2D域和 3D 域的仿射映射。 这和一般的线性系统分析类似。如果我们知道足够数量的基点(或向量)的变换,就可以使用线性叠加来变换每个点(或向量)。将线性拉伸算子视为选择基础及其变换的可视化方式。根据这些信息,COMSOL Multiphysics 自动导出需要应用于任意点(或向量)的映射。 下面,我们将用几个例子来说明这一点。 示例1 第一个算子用于将数据从含有端点1和4的线段映射到含有端点4和5的线段,并保留方向。我们所需要做的就是向 COMSOL Multiphysics 指出哪个点通向哪里,如下图所示。 […]

借助虚构解方法验证仿真
我们该如何检验仿真工具是否正确工作?方法之一就是虚构解方法。该方法涉及假设一个解,获取与假设一致的源项及其他附加条件,使用上述条件作为模拟工具的输入项来求解问题,以及对比结果与假设解。该方法使用简单且用途广泛。例如,桑迪亚国家实验室的研究人员将该方法与一些内部代码一同使用。

参数化扫描、特征频率和瞬态问题的合并解
在之前的博客文章中,我们讨论了在 COMSOL Multiphysics 中求解稳态问题的合并解特征。本篇博文,我们将介绍参数化扫描、特征频率、频域和瞬态问题的合并解。此外,我们还将合并解与内置的 with 算子和 at 算子进行了对比。
