电镀 101

电镀或电沉积是指在金属表面镀上一层其他金属或合金薄层的过程。它可以使廉价的金属看起来很贵重，同时还可以防止腐蚀和生锈，以及增大零件尺寸等优点。

有趣的实例：易拉罐实际上是由 98.5％ 的钢制成的，仅外表电镀了一层薄锡。

常见的电镀物品包括厨房用具、汽车零件和日常配件。

意大利化学家Luigi V. Brugnatelli于1805年发明了电镀。他用钢丝将第一个伏达电堆（Voltaic pile）连接到装有金和金属物体的溶液中。伏达电堆被激活后释放出电流，金被附着在金属物体上，使金属物体具有光泽。Brugnatelli将他的发现发表在Belgian Journal of Physics and Chemistry上，他写道：

“最近，我给两枚大大的银奖章完全地镀上了金。方法是：用钢丝将两枚银奖章与一个伏达电堆的负极连接起来，并将它们依次浸入新制成的饱和金铵溶液中。

Luigi V. Brugnatelli的肖像。图片由Rijksmuseum提供。获CC 1.0许可，通过 Wikimedia Commons共享。

在电镀过程中，将带正电的电极（又称阳极）和带负电的电极（又称阴极）放入电解液中。两个电极都连接到电源，就像电池一样。通电后，电源在电极之间施加电压，最终导致阳极溶解到电解液中，而阴极镀上所需的金属涂层。

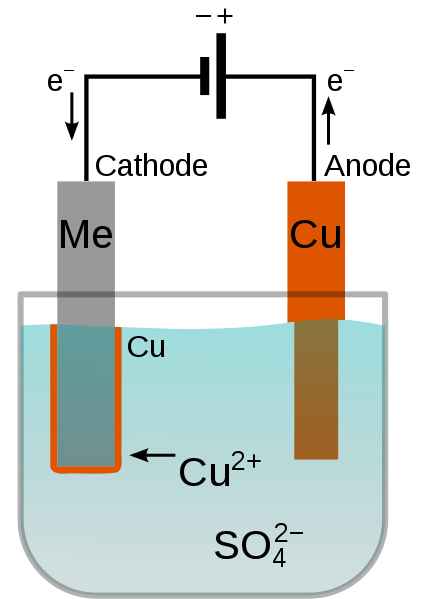
在硫酸铜浴中用铜电镀金属（Me）。图片来自：Wikimedia Commons。

化学电镀工艺的主要原理图

在之前的博客文章中，我们以美国造币厂的电镀铜精铸硬币为例，详细讨论了电镀工艺的工作原理。本文我们将重点介绍如何通过仿真提升挂具上多个工件的电镀效率。

模拟挂镀过程

当电镀复杂的或大型的金属物体时，挂镀是一种常用的方法。与滚镀相比，在汽车、医疗、军事和电子制造等需要高质量饰面的行业中，挂镀是首选的方法。 挂镀也比一次电镀一件的方法要快得多。

挂镀的过程具有一定的挑战性，因为它必须给所有基材或需镀覆的物品上都涂上一层均匀的金属层。借助 COMSOL 软件的电镀模块可以研究几何形状和操作参数对电镀均匀性的影响，有助于优化挂镀过程。

建立几何模型

在建立的模型中，将 20 个机油泵盖安装在挂具中（参考文献2），盖子上均镀了镍。镀镍之所以受欢迎，是因为它具有出色的耐化学腐蚀性能以及更好的耐磨性，从而延长了产品的使用寿命。

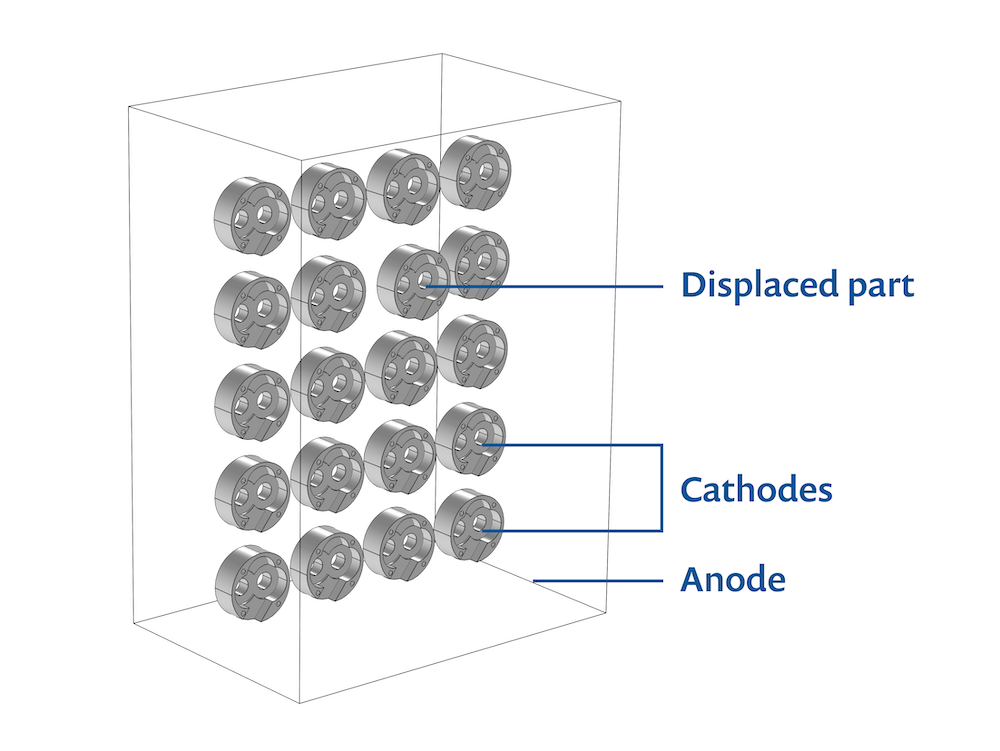
阳极是一个平面的溶解阳极，阴极是油泵盖的阵列。

参数化几何模型，以使油泵盖朝着或远离阳极表面移动。如下图所示，一个油泵盖向阳极移动，以演示几何形状对电解液中电流分布的影响。

下面，我们可以看到单个机油泵盖的几何形状。

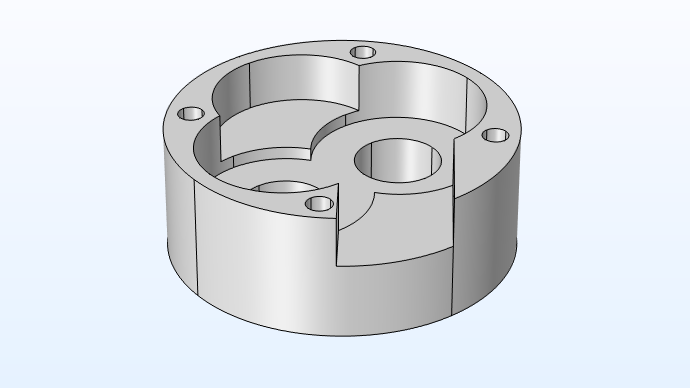
模型使用了二次电流分布接口，并采用 Butler-Volmer 动力学公式描述阳极和阴极的电化学反应，计算得到阴极表面的沉积层厚度。

结果分析

下面，我们可以看到油泵盖或阴极表面上电解液电流密度的流线图和表面图。在电解质中，电流从阳极表面流向阴极表面。总电流密度的表面图显示了整个油泵盖表面（以及它们之间）上不均匀的密度分布。在靠近阳极的油泵盖处，电流密度最高。沿挂具边缘的机油泵盖接收的电流要大于挂具中央的电流。

电流分配不一致的原因是：

1. 油泵盖形状复杂
2. 油泵盖在挂具上的安装位置

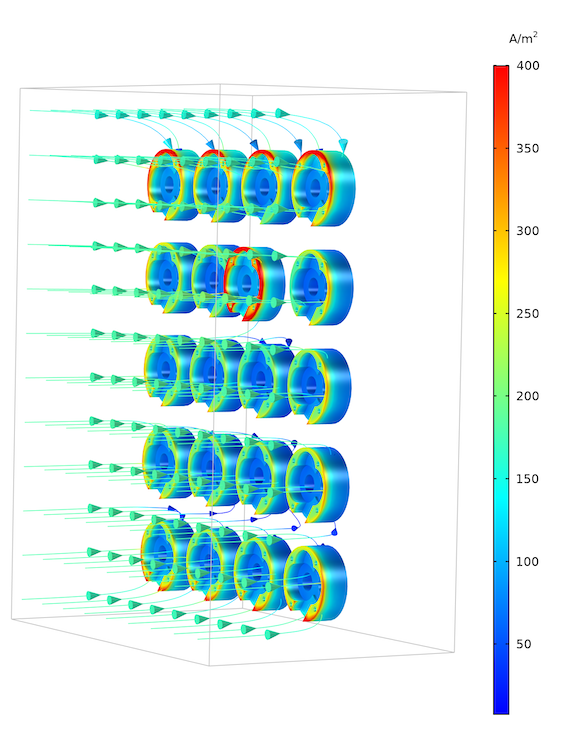
挂具上工件的电流密度分布。该图显示了增厚的阴极上较高的电流密度，以及位于挂具边缘的工件的边缘效应。由于侧面有空间允许更多的电流通过较长的路线到达阴极表面，因此边缘工件的电流密度更高。

接下来，让我们看一下阴极表面上的电镀厚度，这与上述电流密度分布图直接相关。如下图所示，我们可以看到在阴极底部表面沉积厚度最薄，而顶部的沉积厚度最厚。

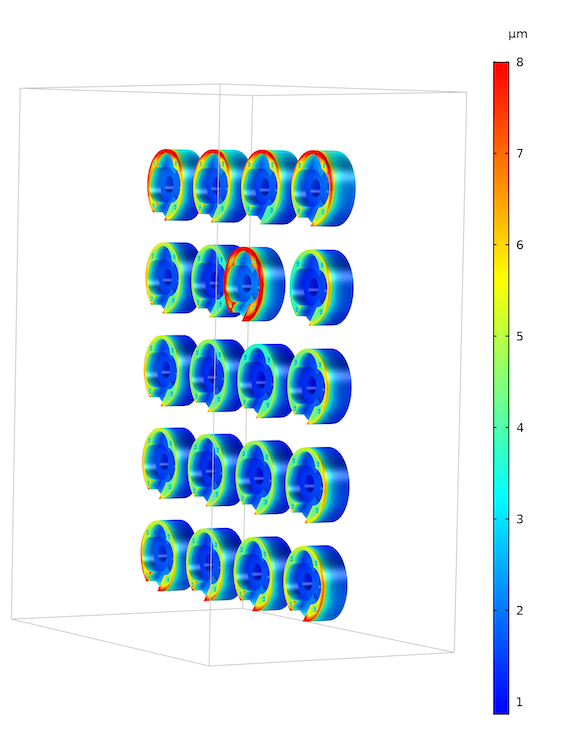
阴极处的电镀厚度。上图中的不均匀电流密度分布也显示在沉积厚度中。电流密度最高的阴极显然沉积物最厚。而且，边缘效应导致放置在挂具边缘的工件镀层变厚。

此数值模型对于优化沉积过程非常有用，它使工程师可以更改设计和操作参数，例如：

• 电镀挂具布置
• 挂具平面的工件排布
• 阳极和阴极表面之间的距离
• 电解质的电导率
• 施加电流
• 电极电势

下一步

单击下面的按钮，进入 COMSOL 应用程序库，尝试对挂具中多个工件的电镀过程建模。请注意，您需要一个 COMSOL Access 帐户和有效的软件许可证，才能下载 MPH 文件。

延展阅读

了解有关电镀的更多信息，请阅读 COMSOL 博客文章：

• 电镀法的艺术与科学
• 零经验进行 PCB 板电镀仿真

1. C. Bell, “What You Probably Never Realized About Award Show Trophies“, Reader’s Digest, 2019.
2. J. Deconinck, G. Floridor, B. Van den Bossche, L. Bortels and G. Nelissen, “Numerical 3D BEM Simulation of the Chromium Layer Thickness Distribution on Parts in a Rack Plating Configuration”, Simulation of Electrochemical Processes, vol. 48, p. 173, 2005.

什么是反向脉冲电镀？

电镀过程涉及将金属电极浸入电解液槽中，然后在电极上施加外部电流。在阴极，槽中离子在其上还原，形成金属镀层。阳极可以是不溶性阳极，其中发生析氧或析氯反应，也可以是溶解性的电极（也称为退镀），其中电极会被氧化，使得金属作为离子进入溶液。

家具配件的装饰性电镀模型 。

在电镀过程中，通常可以施加直流（direct current，DC）或电流脉冲。脉冲电流技术是在一定时间间隔内施加正向电流，其间插入短间隔的大电流反向脉冲或零电流周期。这些电流脉冲间隔的设置也称为占空比。在 RPP 工艺中，我们使用相同或不同幅度、持续时间和极性的电流脉冲来进行电镀和退镀。

RPP 由正向占空比（ ）和反向占空比（ ）组成，在正向占空比（ ）下，施加阴极电流，进行金属沉积（电镀），在反向占空比（ ）下，电镀电流变为反向，进行金属离子溶解（退镀）。在每个方向（正向和反向），占空比定义为电镀/溶解时间与施加电流总时间的比值。占空比的平均电流密度由下式给出：

其中， 和 分别是正向和反向占空比，两者之间的关系为 。

通过优化电镀和退镀工艺以及控制占空比，我们可以使用 RPP 工艺制备光滑的镀层。对于恒定的平均电流密度（ ）和溶解电流密度（ ），电镀电流密度 可定义为：

量化电流分布

根据 IUPAC 定义，当活化过电位的影响不可忽略而浓度过电位可忽略时，二次电流分布有效。当包含活化过电位时，高局部电流密度在电极表面引入高局部活化过电位，使电流自然地变得更加均匀。（有关更多信息，请阅读关于电流分布理论 以及如何选择电流分布接口的博客文章。）

二次电流分布通常用瓦格纳数（ ）来分析，这是一个无量纲量，由下式给出：

其中 ，是电解质槽的电导率；是在上述条件下过电位-电流曲线的斜率；是系统的特征长度（例如，电极长度）。因此，瓦格纳数也可被视为一次电流分布效应（由表示，受几何结构和电解质特性的影响）与二次电流分布效应（由表示，动力学极化）之比。

在 Tafel 极限或高（阳极或阴极）过电位条件下，与工艺的电流密度成反比：

其中，是 Tafel 斜率。

较高的瓦格纳数本质上意味着一次电流分布效应被二次电流效应取代，会产生更均匀的电流分布。另外，对于具有尖端和凹陷的几何结构，可通过使用工作电极周围的一次电流密度分布来实现拉平效应。在下面的例子中，我们将看到如何使用 RPP 在具有给定凸起的几何结构上实现更好的表面光滑度。

使用 COMSOL Multiphysics® 为 RPP 建模

“案例下载”中的反向脉冲电镀模型利用二次电流分布 接口来分析活化过电位（反应动力学）和一次电流分布效应（几何效应和电解质电导率）。

我们建立了一个简单的二维几何结构，其中有一个小突起，当受到不同形式的外加电流影响时，该突起可作为形状演化的标志位置（见下图）。二维模型模拟了一个铜衬底，其中包含一个突起。假设电化学电池因为有良好的搅拌使其具有恒定电导率（无浓度梯度）的电解液、可忽略欧姆损耗的阳极和阴极组成。

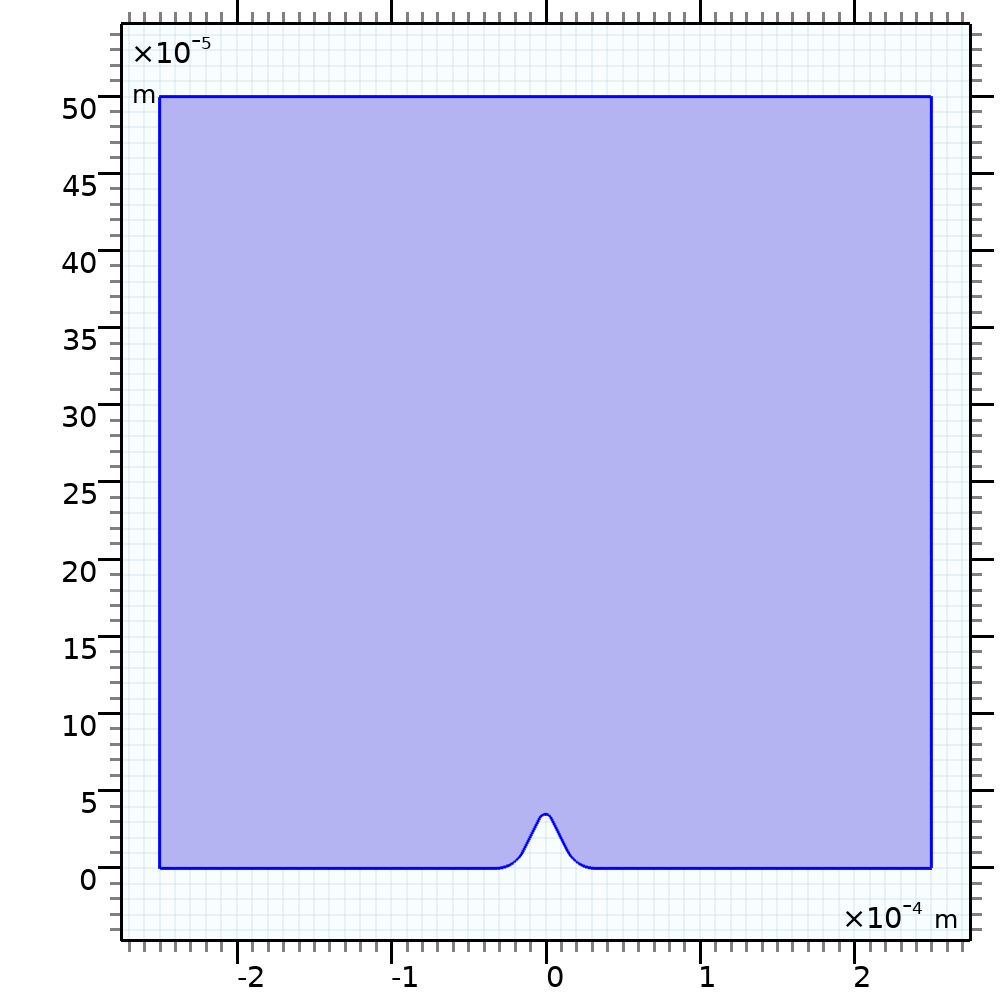
用于建立电镀模型的二维几何结构。

如果要为 RPP 工艺提供参考，我们首先需要建立并求解直流电镀模型。

电解液的电导率为 ，电解液中的电流密度可以根据以下欧姆定律进行描述：

在电极-电解质界面，局部电流（ ）由下式给出：

其中， 由 Butler-Volmer 方程给出：

其中，是交换电流密度；是传递系数；是过电位；是法拉第常数；是气体常数；是温度。

上述方程定义界面上的电荷转移动力学。当考虑欧姆定律和电荷转移动力学这两个过程时，该分析被称为二次电流分布。

电流被施加到对电极的边界表面。在电镀表面，发生了氧化还原反应，该反应的动力学参数（反应速率常数）已知。随后，根据正向和反向脉冲期间局部电流密度的时间平均和来计算电极表面的局部生长速度。在电镀过程中的任意时刻，电极表面的每个点在垂直于电极表面的方向上与局部电流密度成正比：

其中，是摩尔质量；是质量沉积速率；是密度；是沉积铜的化学计量系数。

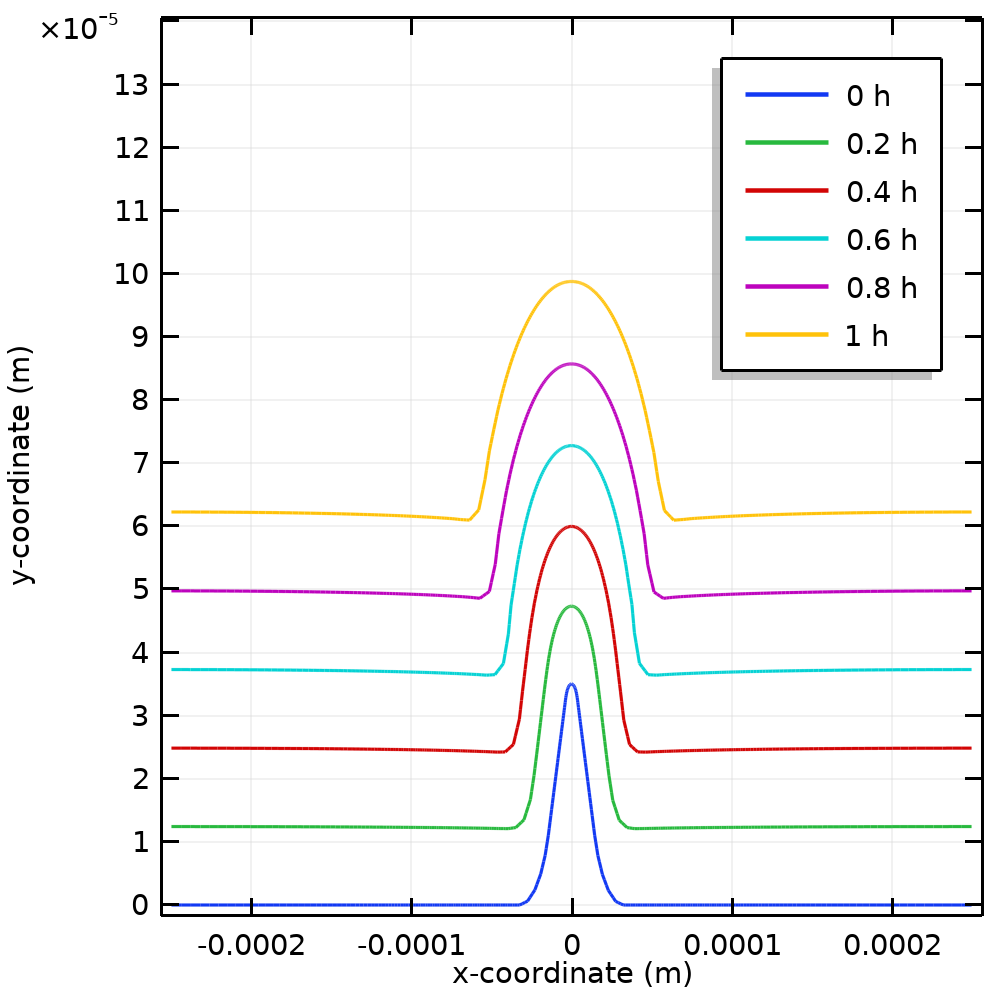
使用直流脉冲电镀时，表面轮廓演变与弧长的关系。

我们设置一小时的瞬态研究，来观察直流电镀情况下指定电流分布条件下的电极形状演变。上图显示了在直流电镀过程中突起如何变得更深更宽。

反向脉冲如何提高电镀工艺水平？

在 RPP 工艺中，电流密度和脉冲宽度等操作参数对于获得理想结果至关重要。通过方程 1可知，工作电极处的平均电流密度与占空比的比率相关。因此，电镀工艺可以通过选择操作循环参数进行微调。接下来，我们继续比较直流模式和 RPP 模式的结果。

我们通过将现有研究中的电解质电流 节点修改为（定义电镀的正向脉冲）并引入额外的二次电流分布 节点来定义溶解（退镀）的叠加反向脉冲，从而建立 RPP 模型。在第二个二次电流分布 节点中，我们将反向脉冲的电解质电流设置为，同时保持动力学参数与先前研究中的参数相同。

平均电解质电流保持恒定，同时仅使用（即正向占空比）改变脉冲宽度。然后，使用方程 2 预测阴极表面的电镀电流密度，并使用方程 8 影响形状演变。我们计算一个小时的瞬态研究，以获得脉冲反向电流的表面轮廓。

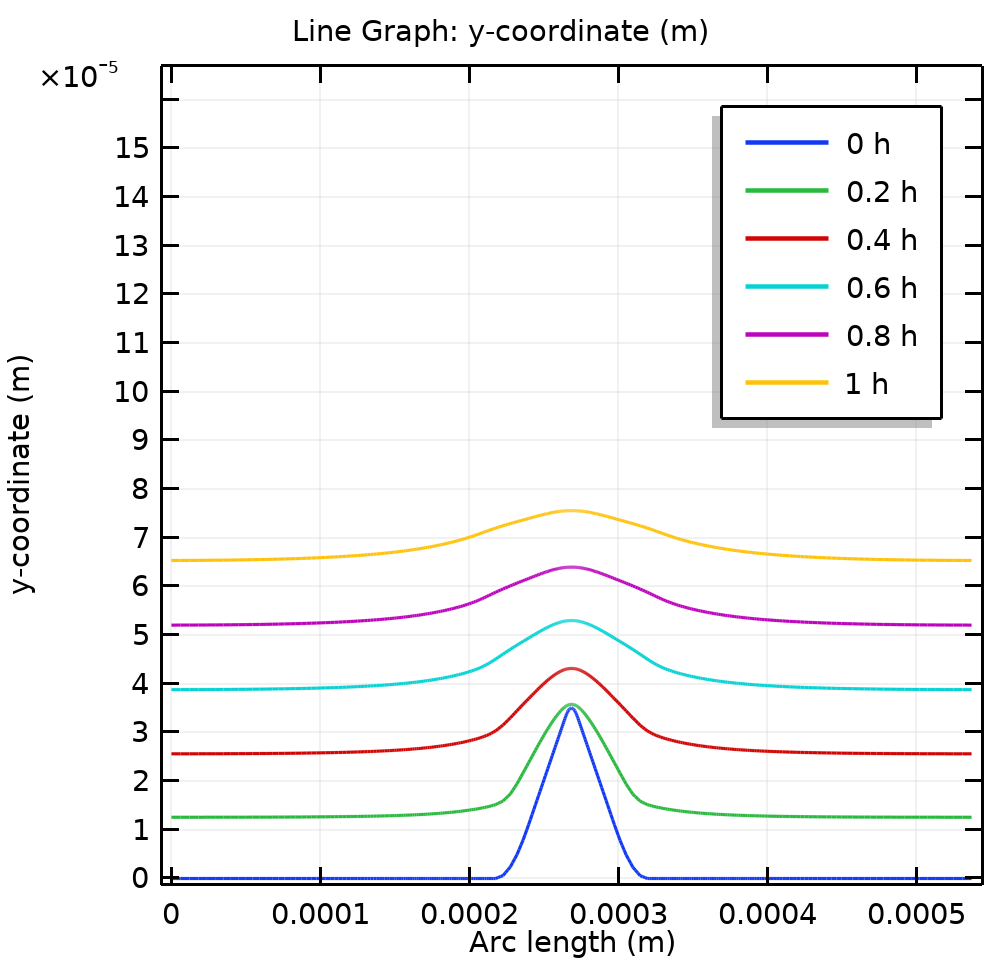
在占空比为 0.85 的情况下，使用 RPP 工艺得到的表面轮廓演变与弧长的关系。

如上所示，与使用相同平均电解质电流的直流电镀相比，表面轮廓的金属表面抛光效果更好。该研究说明，应用脉冲电流可以实现电极表面周围的最佳电流分布。在电极表面使用脉冲电流密度可以在不使用任何电解槽添加剂的情况下获得更平滑的表面轮廓，从而降低与附加化学添加剂相关的成本和毒性。

当使用反向脉冲工艺时，由于我们得到了更高的瞬时电镀电流密度（见方程 2 中的 ），因此电镀工艺的瓦格纳数（ ）总是小于直流工艺时的瓦格纳数，这表明它对几何特征的敏感性；因此，当使用反向脉冲电流时，电流分布的局部化得到增强。我们现在尝试利用局部电流分布通过调整正向和反向脉冲的比率得出一个平滑表面。

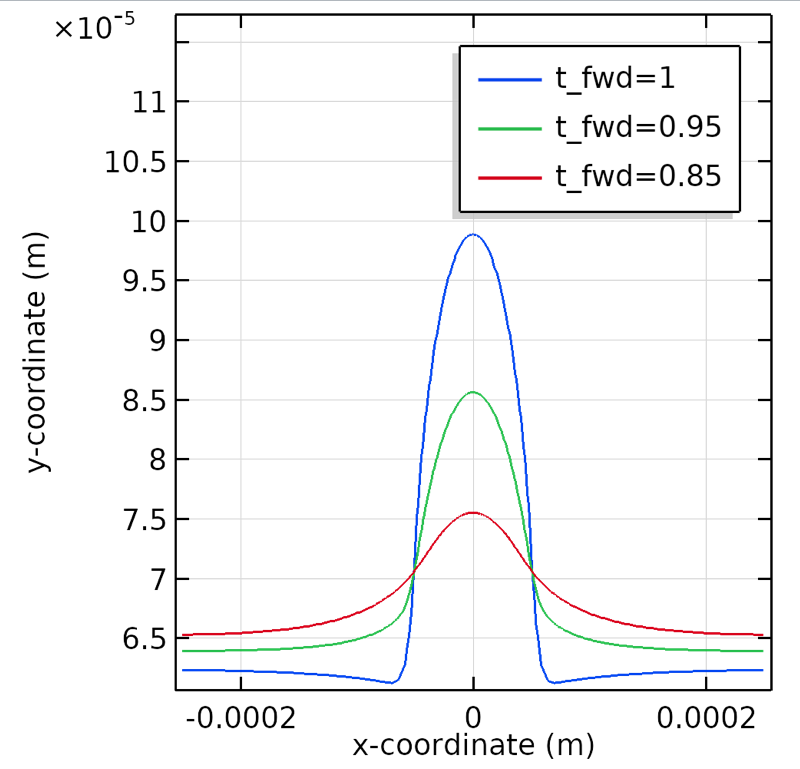
不同占空比情况下使用 RPP 工艺得到的表面轮廓演变与弧长的关系。

在上图中，我们看到了减小反向脉冲电流的正向与反向占空比比率产生的持续磨光效果。对于 RPP 来说，增加反向占空比（ ）会增加溶解时间，并且整体电流分布会变得更不均匀，从而导致不断变化的表面轮廓上出现不同镀速。在这个增加的溶解时段，随着欧姆效应主导溶解过程，在更高的电流密度下溶解反应延长，因此峰凹陷。当我们减小 时，欧姆损耗相对于电镀和反向循环期间的活化损耗变得更大，从而产生对几何敏感的瞬时电流密度分布。通过改变占空比获得的这种电流密度分布使表面更平滑，并且产生突起相对于镀层厚度的几何水准。

结束语

我们讨论了如何使用电流脉冲（而不是额外的化学添加剂）来探索电镀电流操作条件，以使电镀表面尽可能光滑。对于具有已知动力学参数的系统，瓦格纳数与电流密度成反比，并且可以进行相应的调整，从而在表面上实现预期的电镀效果。如果我们想填补裂缝或使波峰凹陷，则应该瞄准瓦格纳数较低的系统，如本例所述。当表面需要均匀的涂层厚度时，我们应在电镀工艺中使用较高的瓦格纳数。用于 RPP 的电流脉冲的正向占空比越小，瓦格纳数越低，从而可以打磨掉小凸起和小缺陷。这是电镀科学中的一门艺术：在不真正影响电解槽化学成分的情况下调整操作条件，并且不需要化学添加剂。

该模型演示了以下功能：

• 与直流电镀工艺相比，RPP 获得了更平滑的表面轮廓
• RPP 脉冲宽度的选择可以显著改变工作电极上的电流分布
• 通过调整正向与反向占空比的比率，可以获得更平滑的光洁度

在仿真中调整操作参数有助于我们理解在相同电解槽中使用 RPP 技术相对于使用直流电镀的优势。因此，仿真提供了一种工具，可以最大限度地减少化学添加剂的使用，减小毒性，降低成本和维护费用。对于化学等效的电解槽，RPP 提供了比直流电镀更出色的金属分布和拉平效应。

后续操作

了解更多关于如何在 COMSOL Multiphysics 中模拟 RPP 工艺的信息。单击下面的按钮进入“案例下载”页面，其中包含 MPH 文件（请注意，你必须拥有 COMSOL Access 帐户和有效的软件许可证）。

你还可以查看电化学抛光模型，该模型是使用电流 接口针对二维几何结构定义的。

利用电沉积制造印刷电路板

简而言之，电沉积 是一种使用其他材料给基底上涂层的电化学过程。这种工艺兼具装饰功能和实用功能，可用于各种不同领域，如电子、采矿和纳米技术。电镀 属于电沉积的一种，主要用途是电路板制造。

PCB 通常由一层或多层铜制成，这些铜沉积在非导电基底之上或之间。铜层被分割成导线或在 PCB 中传输信号的走线。在印制这些图形线路时，工程师会将铜电镀到电路板上的微腔中。

PCB 实例。图片来自 AB Open。在 CC BY 2.0 许可下使用，通过 Flickr Creative Commons 分享。

利用电镀工艺制造 PCB 需要克服许多难题。举例来说，如果 PCB 表面的镀铜速率发生变化，可能会导致性能问题甚至是设备故障。为了找到并消除电镀过程中的问题，工程师可以使用 COMSOL Multiphysics® 软件和附加的“电镀模块”。

分析电路板沟槽中铜的电化学沉积过程

本文的示例模拟了带细小沟槽或微腔的电路板上的铜电化学沉积过程。在恒电位控制下的实验室电池充当了电镀电池，阳极与阴极相互靠近。沉积发生后，阴极和阳极的边界开始移动，因此仿真本质上依赖于时间。另外，阴极表面的镀铜沉积速率是不均匀的。

此模型是电沉积的基准模型，它充分说明了 COMSOL® 软件在求解涉及变形几何的电化学问题方面的强大能力。此例使用变形几何分析了电镀过程及空腔对电镀结果的影响。通过使用变形几何，工程师能够研究在电镀过程中阴极边界的生长过程。

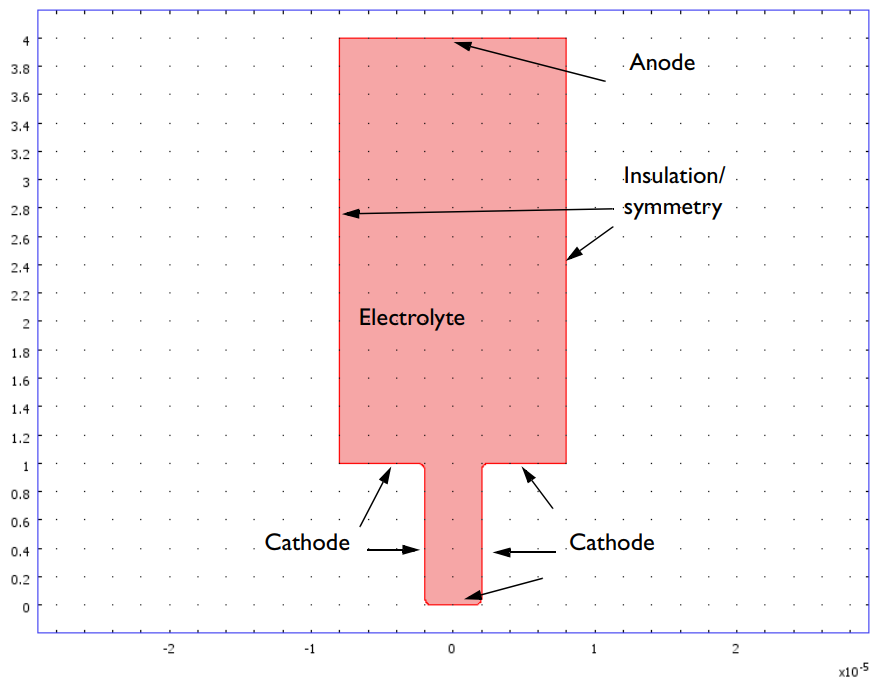
铜沉积的几何模型。垂直的壁表示主电极的图案，壁为绝缘体。

要求解此问题，工程师可以使用内置的任意拉格朗日-欧拉（ALE）方法，该方法可以根据底层物理场预测物体的变形或位移。借助 ALE 方法，工程师能够正确地研究高精度电沉积模型中的沉积物形状。

如果您想了解更多有关模型设置的信息，包括 E. Mattsson 和 J.O’M. Bockris 创造的基础模型，请查看此处的模型文档。

铜电化学沉积过程的仿真结果

下面，我们查看 5 秒钟之后铜的沉积过程。此时，整个电池中的铜离子浓度差异巨大。这些差异最终可能导致电池内产生自由对流，不过基准模型没有考虑这一点。我们可以看到沟槽出口开始变窄，这是由于铜沉积厚度不均匀而导致的。

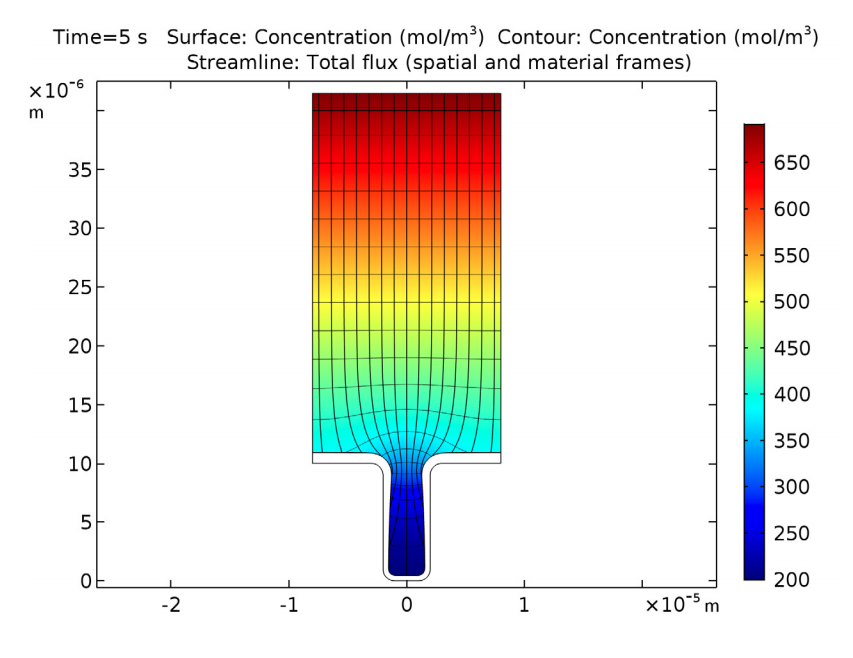
铜离子浓度、等电位线、电流密度流线以及阴极和阳极位移。模型沿电池中间的垂直线呈轴对称。这是个好现象，因为结果不对称说明网格分辨率较差。

下方结果表明，随时间推移，沟槽顶端持续变窄。这会破坏沉积质量，因为被捕获的电解质可能导致电路板组件遭受腐蚀。

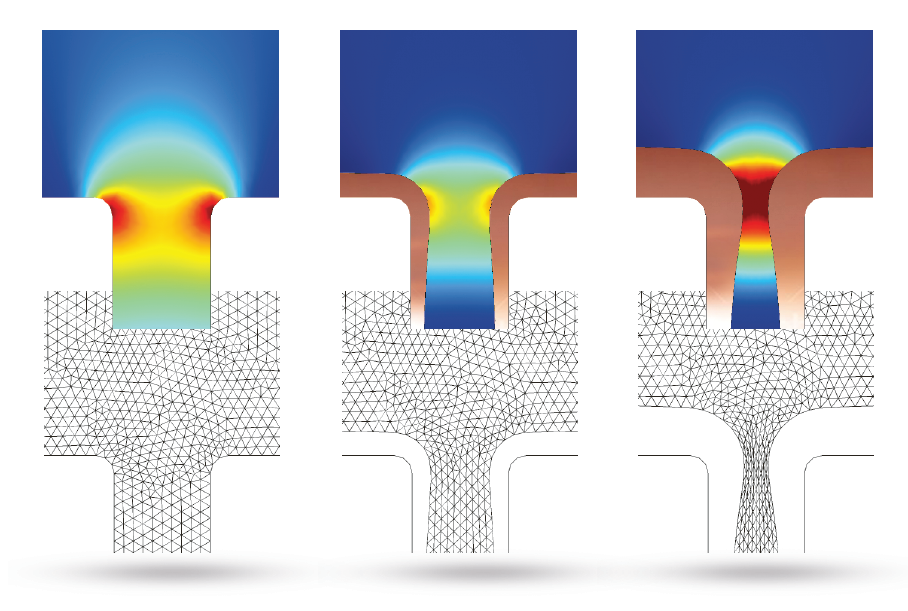
图片（上排）和动画（下排）显示铜材料随时间的沉积过程。图片也突出演示了用于求解此示例的移动网格。

下一张图研究了垂直阴极表面上的沉积层厚度。这张绘图从另一个角度展示了不均匀沉积发生的过程。根本原因在于电流密度分布不均匀，另外，沿腔深度的铜离子不断被消耗，从而加剧不均匀分布。

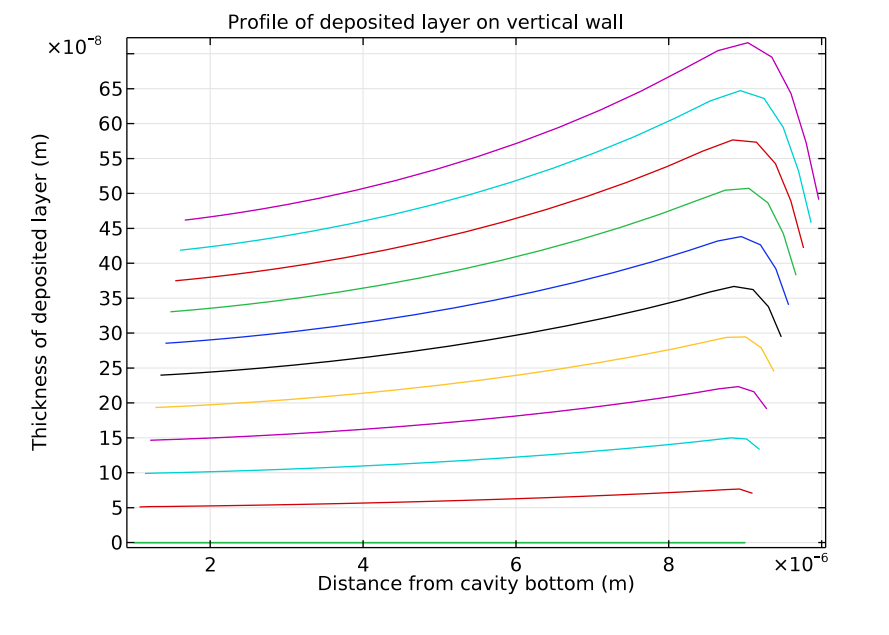
沿垂直阴极边界的沉积层厚度。图中的每条线表示在 0.4~4.4 秒范围每 0.4 秒的增量。

如果需要的话，工程师可以将 ALE 法更换为水平集方法，从而延长这项分析的研究时间，如链接案例所示。这样，我们就可以分析微腔形成之后 的沉积过程，因为水平集方法能够研究拓扑变化。扩展分析表明，不均匀沉积导致形成具有潜在危害的空腔或空隙。与上一轮的 ALE 结果一样，铜离子浓度也显示出了明显变化。

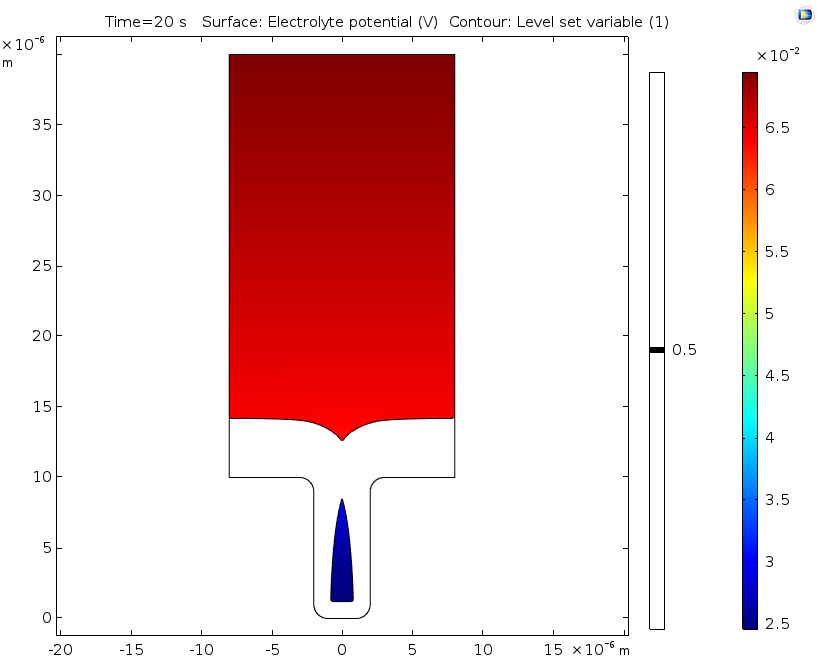
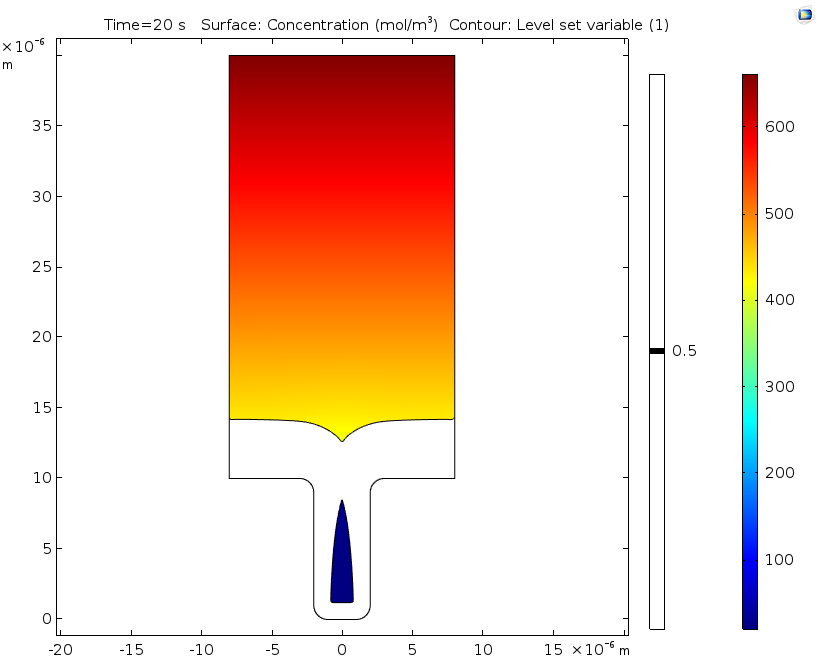
沉积发生了 20 秒后，水平集变量为 0.5 的等值线对应的电解质电位（左）和铜离子浓度（右）。

总而言之，上述结果表明，目前的设计可能会损害沉积层的质量，导致腐蚀和材料浪费。通过数值建模确定这些潜在问题后，工程师就找到了改进设计的突破口……

仿真助力优化铜电化学沉积工艺

借助类似的模型，工程师可以准确地分析电沉积过程，并测试不同的操作参数、施加电位和沉积表面的几何形状。通过这种方式，他们可以找到最优的电沉积参数，提高沉积层的均匀性，从而制造出高质量的产品。

本文中的模型可用作实现这些目标的起点模型。工程师可以根据具体需求来改造此基础模型，例如引入其他离子的影响和测试更多不同的复杂几何。如需自己动手尝试，请单击下方按钮进入“案例下载”页面，如果您拥有有效的软件许可证和 COMSOL Access 帐户，即可此下载相关的 MPH 文件和教程文档。

什么是阻性电流和容性电流？

在描述电路的性能表现时，我们经常会提到电阻和电容。通过阻值为 R (Ω) 的电阻器的电流与外加电压 V 成正比，通过电容值为 C (F) 的电容器的电流与电压变化率成正比：

在电化学电池中，我们可以通过外加电压来测量电流，反过来也同样可行。因此，人们常常从电阻和电容的角度来研究电池的响应。在交流阻抗分析中，阻性电流与外加电压同相，而容性电流与外加电压不同相。虽然我们可以基于测量数据推算电阻和电容，但是许多物理效应都会增加电流的测量值。更有效的方法是对描述电阻和电容效应产生过程的方程式进行求解，方程的结果能帮助我们透彻地理解其中的物理过程。我们使用仿真作为分析测量数据的手段，并结合底层物理原理来进行解释。

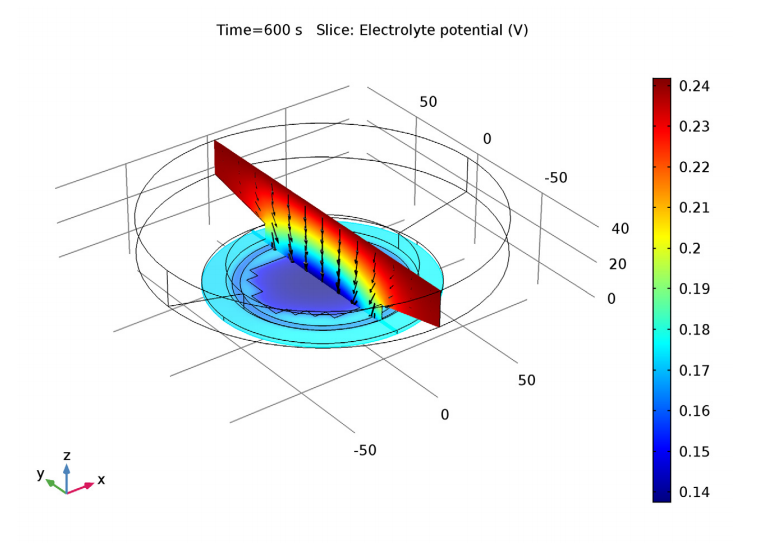
电解质电位图（颜色图）显示了在用于掩膜圆晶片镀铜的电镀槽中，与阻性电流（黑色箭头）相关的电压。镀层的电阻变化也包含在了模型中。

产生电阻和电容的电化学效应

由于电解质的导电能力有限，因此电化学电池中经常需要考虑电阻效应。为了使电流能够通过电极，需要在阴极和阳极之间施加一定的电压，这与使用了常规电阻器的电路是一样的。COMSOL Multiphysics 中的一次电流分布 和二次电流分布 物理场接口可以求解欧姆定律，并据此预测外加电压的大小（通常被称为电阻降），其数值与电解质电导率和电极几何结构之间存在函数关系。

如果无法忽略电极反应动力学的影响，则需要引入额外电压（称作过电位），以抑制发生在电极表面的电化学反应的活化能。常见的电极反应动力学速率定律（例如 Tafel 定律或 Butler-Volmer 方程式）是以过电位的形式对电流密度进行定义的——这里的电流-电压关系可以解释为电阻。然而，与电路中简单的电阻器不同，由电极动力学引起的电阻通常是非线性的。这一点体现在了 Tafel 定律中，即过电位与电流密度的对数成正比。只有外加电压的变化幅度非常小时，电流-电压关系才会呈近似线性，例如电化学阻抗谱。

在电分析和阻抗谱中，人们通常基于电阻和电容的测量值来研究由扩散引起的质量传递。在传统的等效电路分析中，可利用 Warburg 阻抗来解释人们观察到的、由扩散引起的效应。类似地，人们通常使用 Randles 电路来描述上述所有效应的集合，即扩散、电极动力学和溶液电阻。

不过，我们也可以利用对应的物理方程式来直接描述动力学和扩散对电化学电池性能带来的影响。在电分析 接口中，我们对菲克扩散定律与电极动力学关系式（例如 Tafel 或 Butler-Volmer 方程）同时进行求解，直接计算出了基本电化学过程的阻抗谱。在三次电流密度接口中，除了扩散之外，质量传递阻抗还可以引入迁移和对流的贡献。

如果您希望了解在不使用等效电路的情况下，根据物理方程式对电化学阻抗谱进行预测的示例，请参阅电化学阻抗谱教程和锂离子电池案例。

膜阻

当处理电极-电解质交界面上薄层或表面膜的特性这一重要因素时，也需要引入电阻和电容效应。在这些情况下，直接以电阻或电容的形式来表示其特性往往会更简洁明了。

由于电极表面与电极内部的电导率差异较大，因此只要在电极表面创建一个材料薄层，便会产生膜阻。这种额外的阻抗可能导致系统效率降低。如果膜阻出现在电池中，由电化学反应产生的电池电压便会下降，也就是说，外部电路可用的电能变少了。

当暴露在空气中时，大多数金属表面会迅速氧化，直到被一层金属氧化物覆盖。一般来说，金属氧化物比原来的金属导电性更差，由此向系统中引入了额外的膜阻。海底腐蚀便是这种情况，具体情况可参考阳极膜阻效应的案例。

另一个与膜阻相关的示例是电沉积，在此类情况中，电极体材料和表面沉积物质不同。当电导率不同、厚度逐渐增加的物质层在电极表面沉积时，电极表面与电极内部材料属性不同。

在 COMSOL Multiphysics 中，可在电极表面对膜阻进行定义。最直接的方式是设置给定的膜阻，单位为 Ω·m²。单位中包含了 m²，说明了此单位须用来表示单位为 A m^-2、垂直于薄膜的电流密度的局部电阻，薄膜中可驱动电流的电势差单位为 V。另一种方式是我们输入参考膜厚、膜厚变化和薄膜电导率。当薄膜厚度随时间变化时，这些数据将十分有用。

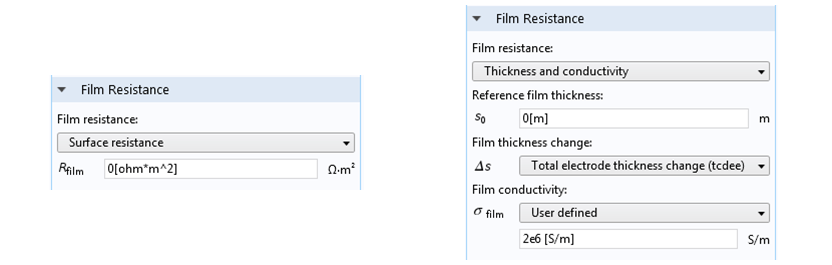
膜阻的设置。左图：电极的表面形状和成分恒定不变、膜阻为常数的情况。右图：在电沉积正在进行时，仿真中的薄膜厚度会发生变化，这是更常见的情况。

双电层电容

带电电极和电解质之间的交界面处会产生被称为双电层（electrical double layer，简称 EDL）的区域。在这块区域中，电荷间的吸引和排斥会导致离子浓度的分布相当不均匀。（在即将发布的博客文章中，我们将更详细地讨论 EDL 的物理场和建模知识。同时推荐您阅读一篇介绍电池中的电流流动的博客文章。）

通过随时间变化的外加电压来改变电极电位，会在双电层中积累或释放电荷。人们使用双电层电容 来描述双电层中积累的电荷量。双电层的尺寸取决于系统中的 Debye 长度，通常为纳米级。相比之下，扩散层或电化学电池的尺寸范围通常在微米到米之间，因此这类电容可以被视为在电极-电解质交界处发生的表面效应。

在 COMSOL Multiphysics 中，您可以使用多种 EDL 建模工具（请参照带电荷传递的扩散双电层教学模型）。COMSOL Multiphysics®5.2a 版发布了全新的 Nernst-Planck-Poisson 方程 多物理场接口，让建模变得空前简单。不过，即使相关的理论成果十分丰富，但设计一个能精确描述 EDL 中实验观察现象的模型仍是无稽之谈。因此，我们优先考虑双电层电容的经验描述，即通过拟合实验数据凭经验定义电容。

在阻抗谱中，高频下电压会迅速变化，因此双电层电容尤为重要。有限的电极反应速率、有限的质量传递速率，再加上双层电容，许多电化学系统的奈奎斯特图常出现的“半圆加尾巴”的特征形状与三者紧密相关。

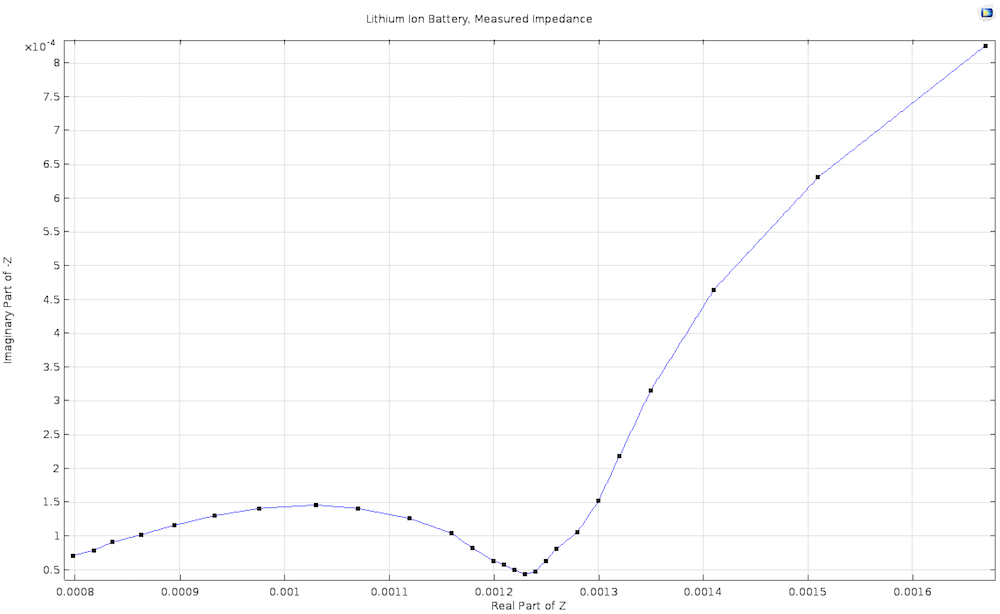
锂离子电池的实验测量奈奎斯特图，来源于锂离子电池的阻抗演示 App。

在定义电极表面时，我们可以添加一个双电层电容 子节点。为了建立这一电极特征，我们须输入单位面积的表面电容（单位为 F m^-2），不过某些情况下还需要额外的输入。以多孔电极为例，多孔基体双电层电容 特征需要输入一个具体表面积，以确定电极-电解质交界面的真实表面积，而我们知道，这个交界面上存在着双电层，并且发生了电容性充电。除此之外，您也可以使用内置工具，根据球体、圆柱体或薄片的粒子属性来计算多孔电极的双电层面积。在这种情况下，您不需要明确了解电极的具体表面积。

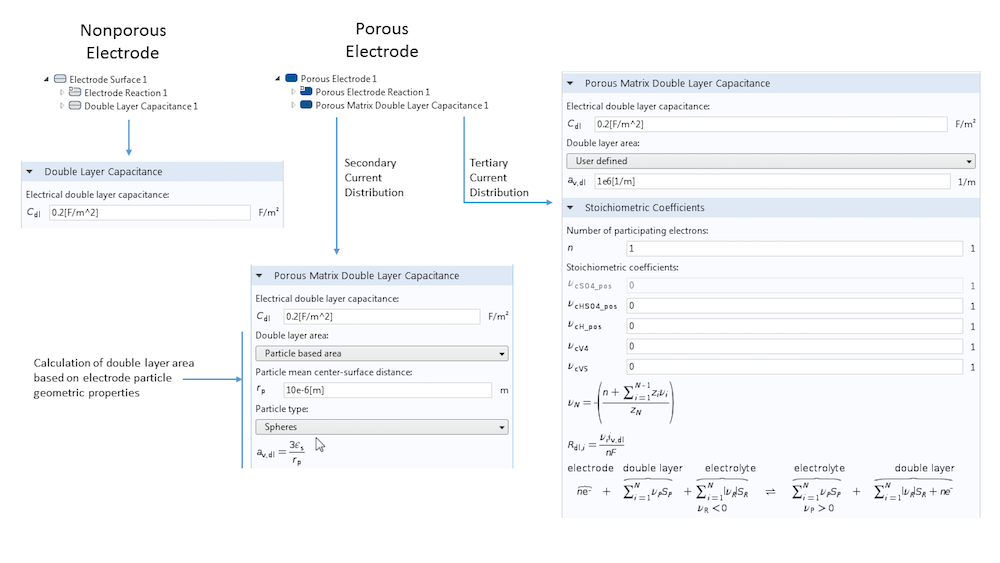
“双电层电容”特征的设置概览。图片显示了无孔电极和多孔电极之间的差异，以及根据某些基本几何属性来计算双电层表面积的可能性，而没有直接将表面积添加为输入的方式。

解决更复杂的电路设置

在少数情况下，建议您将电极连接到更复杂的电路，借此更加清晰地了解电化学系统如何与复杂的驱动电路耦合。COMSOL Multiphysics 再次表现了出色的灵活性，可以将任何电化学物理接口连接到电路 接口。

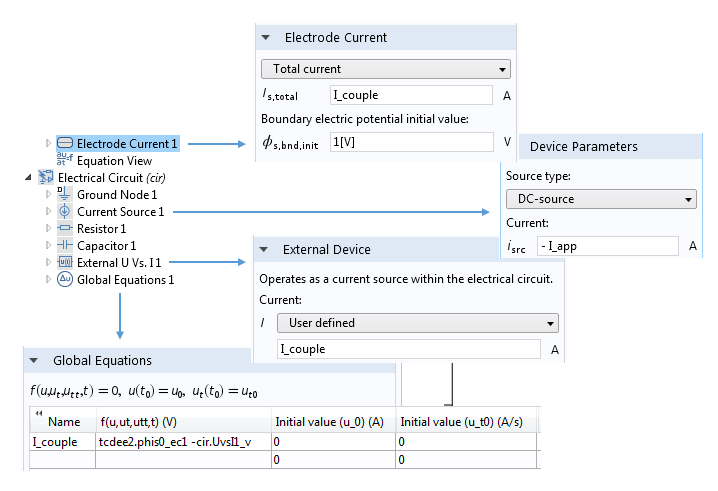
将电流驱动的电化学系统耦合到提供电流激励设备的电路，上图显示了此系统的常规设置。需要特别注意的是 电极电流和 外部设备栏中的电流如何被设置为了共用变量 I_couple。我们对与这两个节点相关联的电压施加约束，使二者相等，由此确定上述变量的值。

通过精确描述电阻和电容提高电化学模型的准确性

在本篇博客文章中，我们解释了如何描述电化学系统的电阻和电容，并详细介绍了每种方法的适用情况。我们建议您将本文中介绍的工具和知识用于实际的建模工作，帮助您最大限度地提高电化学模型的准确度和实用性。

在 COMSOL Multiphysics® 中模拟电化学系统的其他资源

• 如需了解如何在电化学模型中添加电阻和电容特征，请下载以下教程：
  • 电化学阻抗谱
  • 锂离子电池的容量衰减
  • 模拟锂离子电池的阻抗
• 观看已归档的网络研讨会，了解更多有关在 COMSOL Multiphysics 中模拟电化学系统的信息

定制电镀仿真 App 应用程序

可以使用 App 开发器和 COMSOL Multiphysics 5.0 版本中的电镀模块定制电镀 App 应用程序。有了它，PCB 板设计人员可以利用仿真来分析设计和制造过程中的诸多因素。他们可以判断一项设计能否满足铜线规格要求、评估这类器件的表现，同时估算电镀过程的制造成本，而无需具备电镀方面的知识。

电镀铜图形中的设计挑战

常见的 PCB板会使用一层或多层铜线来连接板上的有源和无源器件。另一方面，更高级的 PCB 板中则会使用电镀铜图形来生成线路。实际开始电镀之前，应在 PCB 板上先准备一层图形化绝缘膜。这一过程通过以下几个步骤实现。

在 PCB 板上准备一层图形化绝缘膜

第一步是在 PCB 板上镀一层薄薄的导电铜种子层。接下来，PCB 板的表面需要再涂上一层光刻胶（光敏聚合物薄膜），这一过程通常称作光刻。该过程会将覆盖了图形化掩膜板的光刻胶置于紫外线之下，曝光区域发生溶解。结果是得到了带有图形化绝缘膜、且已露出图形底部种子层的 PCB 板。

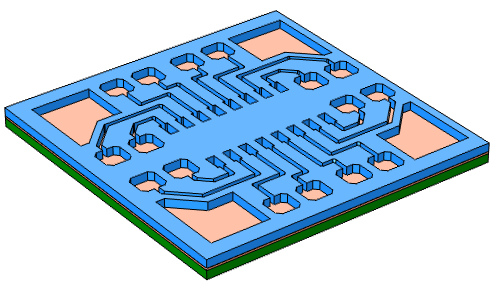
将种子层镀于 PCB 板之上（左）。通过光刻法利用光刻胶绘制 PCB 板图形（右）。

在电镀过程中，PCB 板和铜阳极（例如实心铜条）被浸入电镀槽，其中包含硫酸和硫酸铜的电解液。在阳极和种子层阴极之间施加一个电压，这会引起电化学还原反应，铜离子被还原到镀（沉积）在种子层上的铜金属之中。随着时间的推移，镀层厚度直接与电化学反应的速率成正比，而速率则由种子层不同位置处的电流密度所确定。因此，图形化光刻胶腔体中填满了固体铜。可通过控制平均电流密度来保持电镀速度（例如，待镀图形化区域中的总电流大小）。

最后，清除剩余的光刻胶，蚀刻薄种子层以分隔开不同的镀铜线。

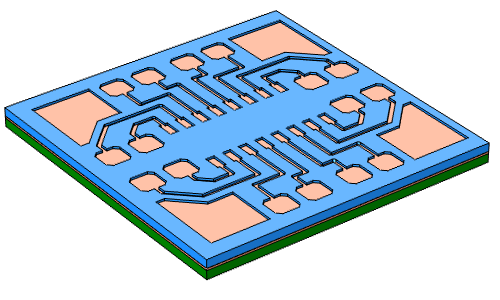
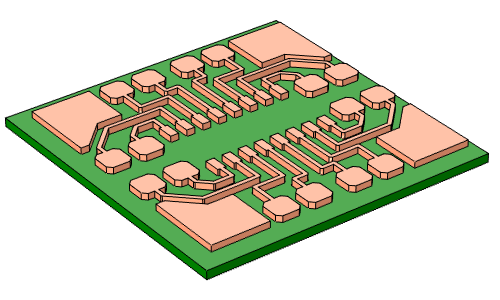
铜被电镀在导电种子层之上，从而填满了 PCB 板上的图形化光刻胶腔体（左）。清除光刻胶，蚀刻暴露出的种子层以分隔开不同的铜线（右）。

电镀速度的均匀性

该过程中已知的一个问题是，整个 PCB 板中的电镀速度并非总能保持均匀。电解液中的电场集中于被大块绝缘区域所包围的导电图形，以及靠近 PCB 板边缘的图形处。电场的非均匀性在这些区域的阴极表面产生了更高的局部电流密度，该效应通常称为电流丛聚。随着时间的推移，镀层厚度与电流密度成正比，这会在 PCB 板中造成我们所不希望的铜线厚度变化。这意味着 PCB 板不同位置处铜线间的电阻会有差异。当 PCB 板用于电子器件时，这种厚度变化可能是性能问题，甚至在最坏的情况下，引发器件故障的根源所在。

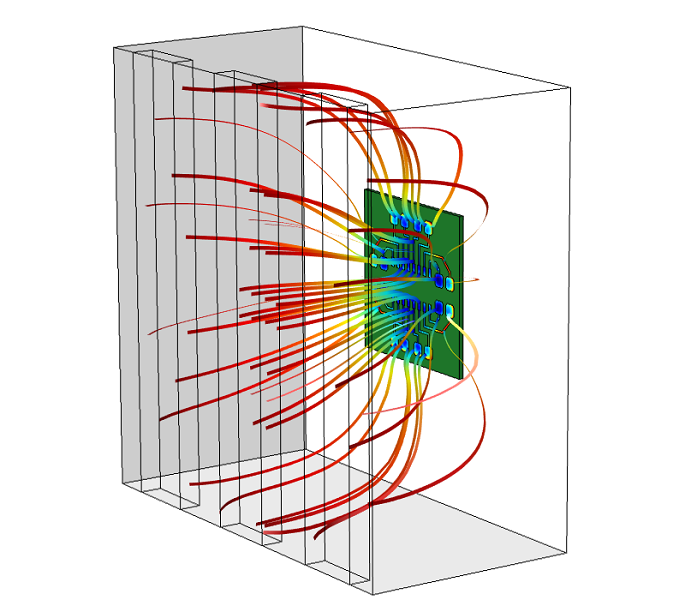
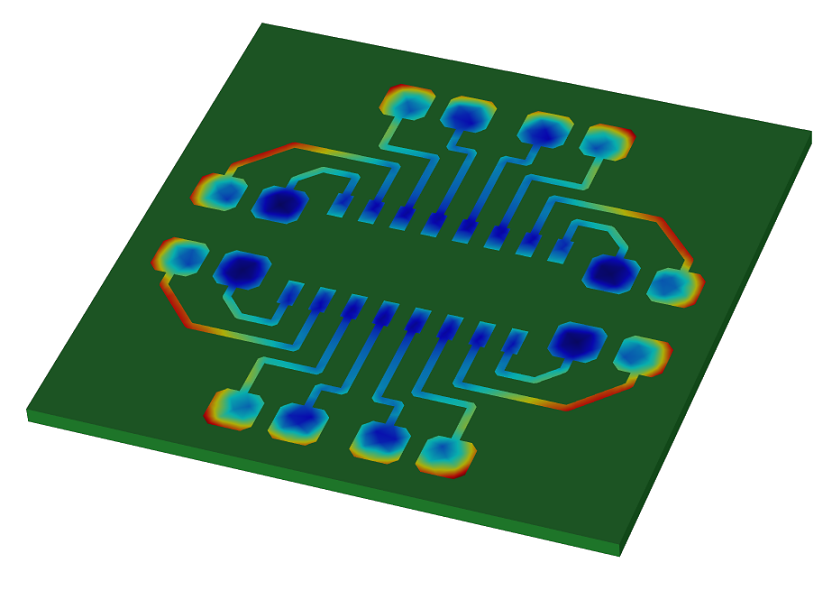
在电镀铜图形的步骤中，PCB 板和铜阳极被浸在电镀槽（电解液）中（左）。在阳极和 PCB 板之间施加电压后，铜会沉积并形成导线图形。从阳极到 PCB 板导电部分的电场在靠近大块绝缘区域以及 PCB 板边缘处出现丛聚（左图中以彩色电场线图显示）。这将在这些区域形成更高的局部铜厚度（参见右图导线图形中的红色部分）。

设计阶段的仿真和优化

为避免在电子器件的运行中出现性能下降或器件故障，铜线电路必须满足一套厚度均匀性的规格。通常情况下，印刷电路板的设计人员会依赖一些简单的设计规则，例如最大与最小线宽、间距，以及图形密度。然而，通过电镀仿真，可以更精确地计算能达到的预期铜层厚度变化。有了这一信息，就可以在早期修改设计，而无需等待原型机结果。

为了降低电流丛聚，可以在通常是大块绝缘区域的位置加入“虚置”图形设计。此时，虚置图形会接受部分电流，这将降低实际布线图中的高电流密度。虚置图形的部分区域仍会有较高的电流密度，但由于它并非实际布线的一部分，所以没有关系。通过仿真，可以快速简单地重新设计并计算不同图形布局所得到的厚度均匀性。

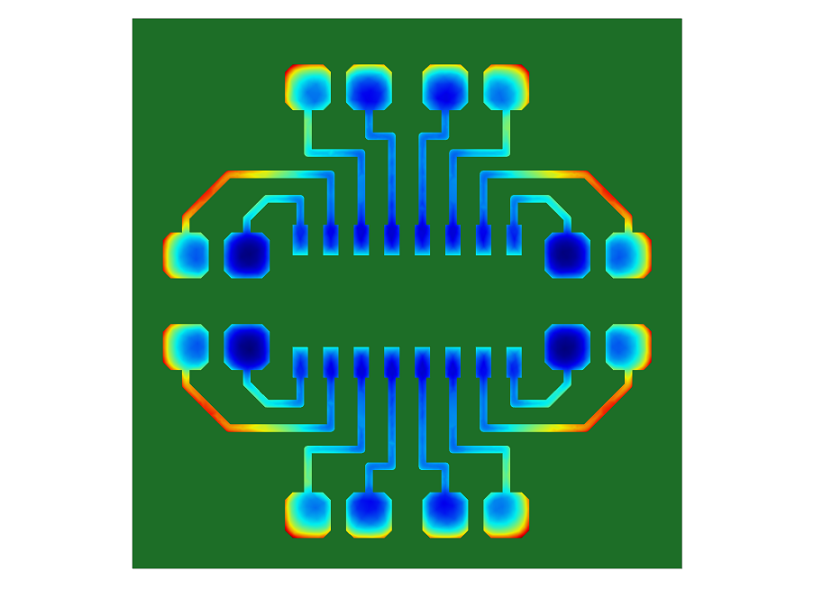
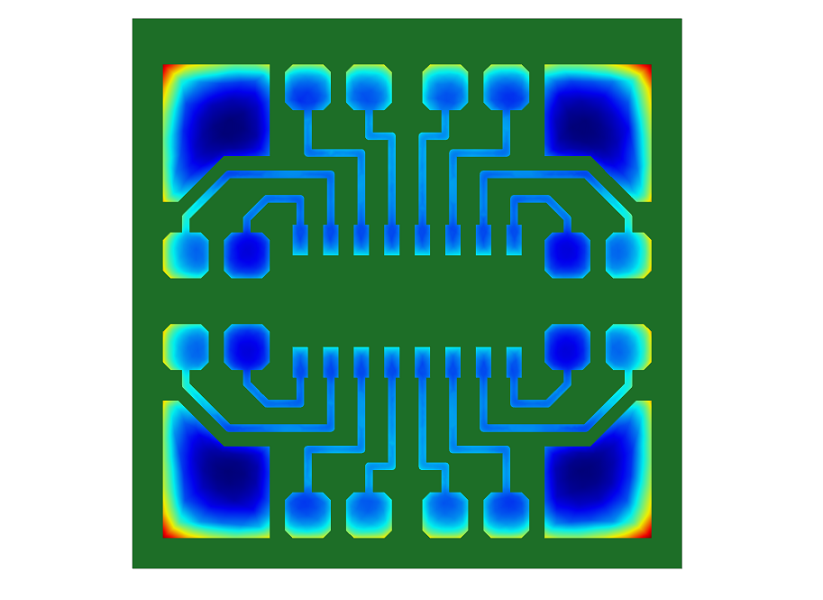
为了减小铜图形的厚度变化，可在通常是大块绝缘区域的位置加入虚置图形。左图中，红色区域显示靠近绝缘区域的铜图形中厚度较高的部分。右图显示了如何加入虚置图形以降低铜布线图形中的厚度变化。

减小厚度变化的另外一个步骤与电镀槽设置有关。为降低边缘处的电流丛聚效应，可以使用称为孔隙的器件。

孔隙本质上是带有开口的一个绝缘屏蔽层，在电镀槽中，它被放置在铜阳极和 PCB 板之间。孔隙开口的尺寸必须小于 PCB 板的尺寸，以降低边缘处的电流丛聚。除此之外，很难估计出孔隙的最佳尺寸和安置位置。

幸运的是，通过仿真可以快速简单地进行优化。下图模拟了带有矩形开口的孔隙。孔隙开口的长度与宽度及其在电镀槽中的放置位置得到了优化，从而使 PCB 板上的厚度变化降到最低。

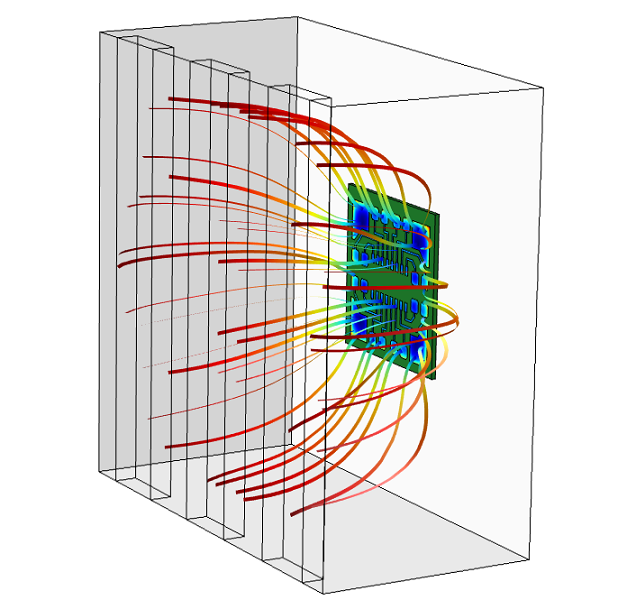
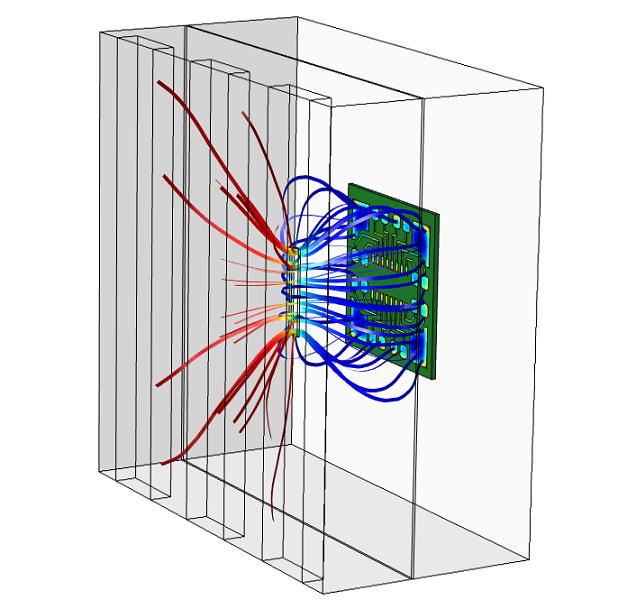
为了避免靠近 PCB 板边缘处的丛聚效应（如左图所示），可在电镀槽的阳极和之间放置一个带有开口的孔隙，即绝缘屏蔽层。右图显示了经仿真优化后可以达到最小厚度变化的孔隙开口大小，及其在电镀槽中的放置位置。

制造成本方面的考虑

PCB 板制造商如要拥有竞争力，就必须考虑制造成本。如前所述，最终产品总是需要满足一个铜厚度均匀性规格。厚度均匀性本质上取决于电镀过程中的总电镀速度；整体速度越高，厚度变化越大。此外，总加工时间决定了生产线的生产量，因此，也决定了制造成本。

成本最小化

为了最小化制造成本，加工会按照能满足厚度规格的最大可能速度进行。通过使用仿真研究电镀速度的影响，可以计算出针对给定厚度均匀性规格应采用的电镀速度。这使我们在设计阶段就能估算出制造成本。

通过改进设计，或使用孔隙来改进均匀性，可以模拟得到能够支持的最高电镀速度，以及 PCB 板生产中可以节省的成本。

通过电镀 App 运行仿真

拥有电化学背景，同时理解仿真模型和软件的人士创建了电镀仿真模型。PCB 板设计人员通常擅长电气设计，但对制造中的电化学过程了解不多或完全没有相关知识。

我们已经讨论了电镀仿真的诸多优势，但如何才能使 PCB 板设计人员使用上仿真模型呢？

创建 App

解决方案之一是创建界面易于使用的定制电镀 App，这使 PCB 板设计人员可以研究一些重要参数，同时只需点击几下鼠标就能运行仿真。

利用 COMSOL Multiphysics 5.0 版本中所带的 App 开发器，仿真专家们只需投入很少的精力就可以创建出这类 App，从而使组织中的其他人都可以运行仿真。

电镀 App 允许 PCB 板设计人员导入不同的设计（包含或不含虚置图形），点击计算，然后就能查看所仿真的厚度均匀性。也可以改变电镀槽和阳极的尺寸，或加入一个孔隙。只需简单一个点击，即可运行 App 来优化孔隙的尺寸和放置位置。最后，可利用 App 找出针对给定厚度均匀性规格的最高电镀速度。通过这一信息，可以计算出制造成本。

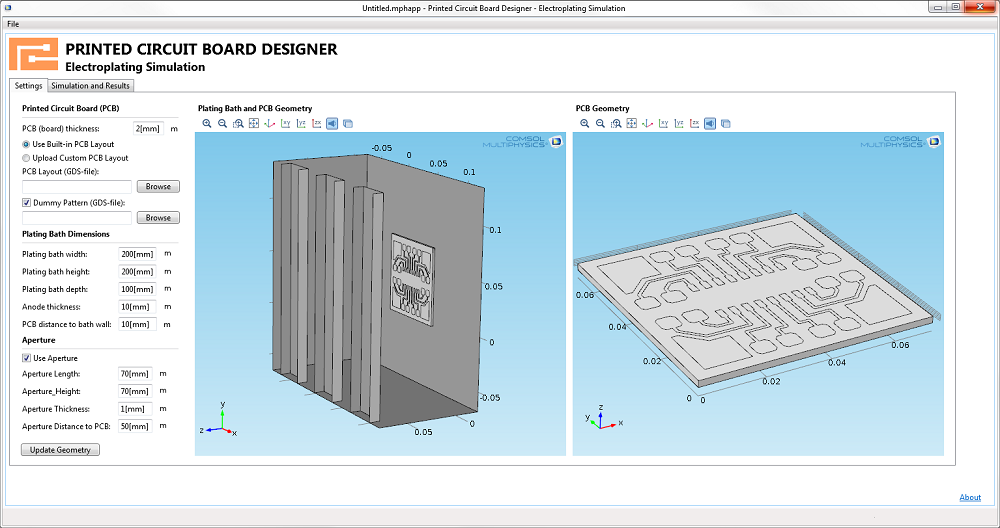
电镀 App 的用户界面。它支持 PCB 板设计人员上传不同的设计，修改电镀槽尺寸，以及加入特定尺寸的孔隙（可选）。

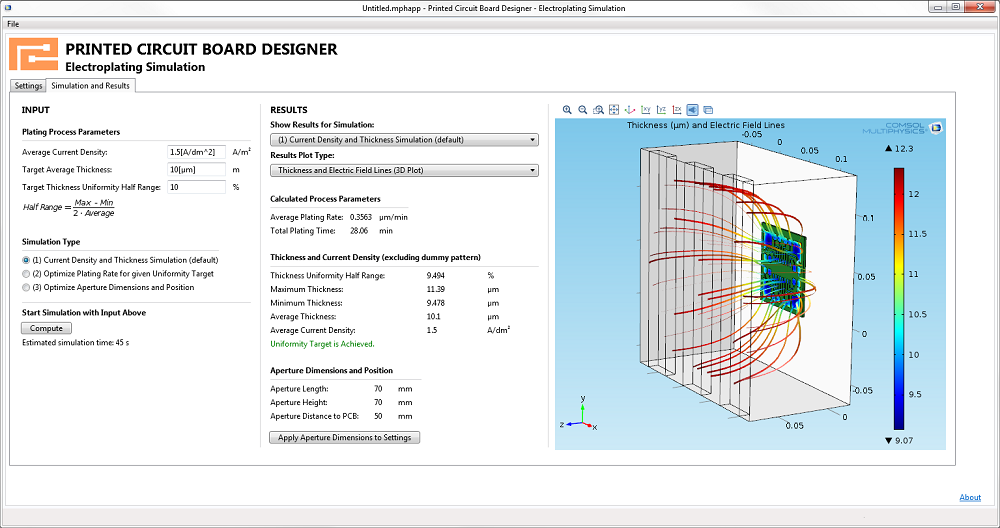
有了电镀 App，用户只需简单点击就可以运行仿真。用户可以研究铜线厚度的均匀性，以及不同设计、电镀速度和电镀槽设置对它的影响。此外，也可以运行 App 来仿真用于减少厚度变化的最佳孔隙尺寸。最后，App 可用于计算针对给定的厚度均匀性目标、所支持的最高电镀速度。

结束语

我们已经讨论了仿真对于使用电镀铜图形工艺的高级 PCB 板而言的重要性。在设计阶段运行电镀真，可以减少由于电镀过程中的厚度变化而产生的性能下降，甚至可以减少器件故障。

传统意义上，这类仿真模型并非由 PCB 板设计人员所操作，更多的是电镀和仿真专家们的工作。但是，通过构建界面易于使用的专业电镀 App，我们可以将电镀仿真带给 PCB 板设计人员。设计人员能够在日常工作中运行仿真，并充分享受它带来的各种优势。

最后，通过减少原型机的数量以及优化设计和工艺来最小化制造成本，资金得到了节省。进一步而言，类似的 App 可以加入到制造过程中，由负责此阶段的工程和技术人员运行。这使他们可以自行对电镀的操作进行微调和校准，以及辅助进行质量保证。

扩展阅读

• 了解更多关于 App 开发器的信息
• 研究电镀模块

三种电流分布接口

与上一篇博客文章一样，我们可以借助线电极模型的案例比较三种电流分布接口。下方是线电极的几何结构示意图：

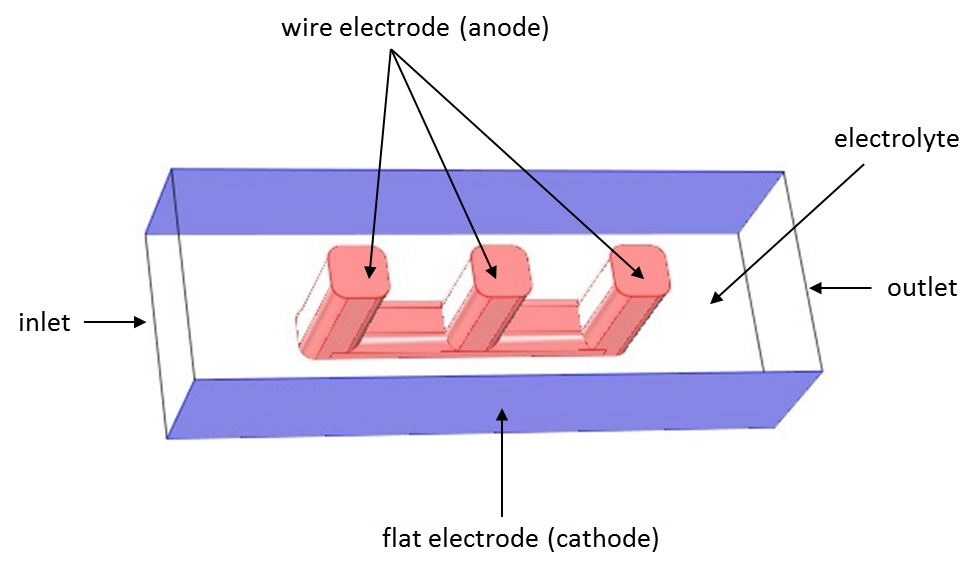
使用 COMSOL Multiphysics 求解的线电极模型。电解质可以在导线和平坦表面之间的开放空间内流动。

本文提及的三种电流分布情形采用了相同的几何模型：在两个平坦的电极表面之间放置一个线电极结构。该电化学单元电池可视为一个体积更大的线网格电极中的一个单元，后者是许多大规模工业生产过程中常见的电化学电池装置。

回顾基本方程

以下是我们在上一篇博客中详细说明的基本方程式：

Nernst-Planck 方程：

(1)

包含 Nernst-Planck 方程的电流密度表达式：

(2)

一般电解质电流守恒：

一次电流分布

一次电流分布仅适用于解释溶液电阻造成的损耗，而忽略了电极动力学和浓度依赖性效应造成的损耗。它假定电解液中的电荷转移遵守欧姆定律。在这里，我们做出了两个假设：第一，电解质是电中性的，它抵消了对流项在表达式（2）中对电流密度的贡献；第二，电解质的成分变化微不足道（即分布均匀），这抵消了扩散项在表达式（2）中对电流密度的贡献，允许我们将离子强度看作一个常数。由此一来，表达式（2）的剩余项即为欧姆定律用于描述电解质电流密度。

我们认为，电极-电解质界面上的电解反应发生得非常快，以至于可以忽略电极动力学的影响，因此，电极-电解质界面上的电势差基本不会偏离平衡值。换句话说，没有活化过电位，而且通过电解会产生任意的电流密度。由此可见，一次电流分布仅取决于正极和负极的几何构造。

COMSOL Multiphysics 的一次电流分布 接口定义了两个相关变量：一个是电解质电势（），另一个是电极电势（）。基于上述的一次电流分布假设，可得以下方程:

电极： 和

电解质： 和

电极与电解质界面：

其中， 表示电解质的电导率，根据上述假设它是一个常数。下标 代表电极， 代表电解质。 表示反应 的平衡电位。

在下图中，我们展示了线电极示例的一次电流密度分布。如您所见，电流密度分布在直面负极板的导线的拐角处，在导线结构的中心区域则趋近于零，原因是从几何结构上该区域与负极隔开了。

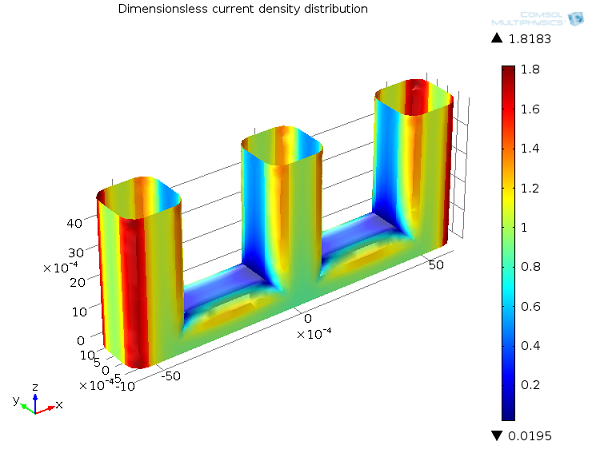
一次电流分布，Ecell = 1.65 V。正极上的电流密度分布（无量纲）。

何时使用一次电流分布 接口？

如果电池的电解质浓度（相对于电流密度）较高，或者经剧烈搅拌混合后，电解质浓度可以假设为均匀。并且，电化学反应速度非常快，以至于反应电阻的大小与电阻损耗（溶液电阻）相比可忽略不计。如此，便可以使用一次电流分布来模拟电池。

上述条件的应用之一是在施加外加电流阴极保护系统的阳极上，与此同时，在一次电流密度分布接口中，我们可以将相当于氧还原反应中受质量传递限制的电流，以恒定电流的条件设为阴极的边界条件（参照案例）。这也是对反应速度相对较快的电化学过程的一个有效近似，例如氯碱工艺流程中氯离子的快速氧化。

由于一次电流分布 接口易于求解，且不涉及非线性动力学表达式，因此通常适合于计算基准近似结果，为处理较复杂的模型做好准备。

二次电流分布

二次电流分布用于解释电极动力学和溶液电阻的影响。它关于电解质的组成和特性的假设与一次电流分布是一致的，也就是说电解质电流同样遵守欧姆定律。一次和二次电流分布的区别在于对电解质和电极界面上的电化学反应的描述。

二次电流分布引入了电极动力学的影响；由于电解反应速率有限导致额外的阻抗，电位差可能偏离其平衡值。实际电位差和平衡电位差的差值即活化过电位（）。因此，你会发现一次电流分布 和二次电流分布 接口的域方程完全相同，但是由于过电位的存在，电极-电解质界面的电位方程式存在差别:

电极： 和

电解质： 和

电极与电解质界面：

在二次电流分布 接口中，由于电化学反应而产生的电流密度被描述为过电位的函数。物理场接口可以使用电流密度和过电位之间的任何关系，例如 COMSOL 的常用内置选项 Butler-Volmer 方程式（3）和 Tafel 方程式。

(3)

上述 Butler-Volmer 方程针对反应 规定： 代表局部电荷转移电流密度， 代表交换电流密度， 代表阳极电荷传递系数， 代表阴极电荷传递系数。 是通用气体常数。这个方程式描述的情形是：单电子的电荷转移是净电荷转移反应的速率控制步。我们可以以描述均质化学反应的 Arrhenius 方程进行类比，从而推导出方程式，前提是假设带电物质的自由能会受到电位的影响。因此，活化能将随电极-电解质界面的电位差而变化。

根据下方公式，将全部电极的反应电流之和用作电极和电解质域之间边界上的电流密度条件:

附加电容电流 产生于双电层的充电和放电过程。

一般情况下，通过活化过电位来解释电极动力学的影响，往往会使电流分布更加均匀。下图中的线电极示例说明了这一点。

与一次电流分布相比，二次电流分布更加平滑，最小值与最大值之间的差异更小。引入了活化过电位的影响后，局部高电流密度将在电极表面引发高的局部活化过电位，自然导致电流流向其他的路径。换句话说，你可以理解为电化学反应以有限的速率进行。在某些区域，反应动力学受到了限制，因此表面的电流密度分布会比不受限制的快速反应的情形更加平滑。

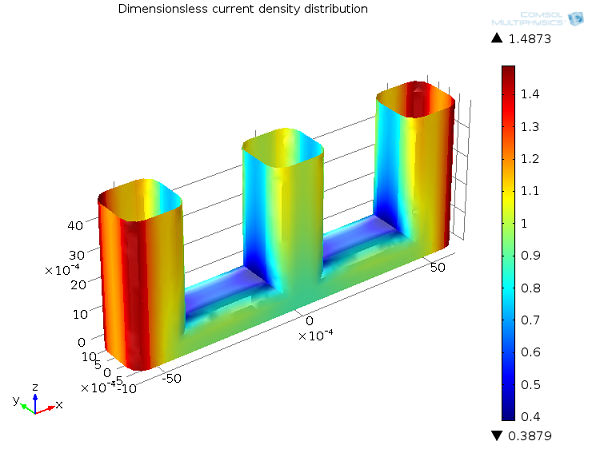
二次电流分布，Ecell = 1.65 V。正极的电流密度分布（无量纲）。

何时使用二次电流分布 接口？

二次电流分布 是电化学工业应用建模的“主力”接口。你可以将二次电流分布用于电池建模，前提是电解质充分混合或浓度相对较高，因而可以忽略浓度过电位，若电极动力学引起的损耗与电阻损耗相比不可忽略，则不可行。众所周知，在工业应用中充分混合高浓度的电解质不是一个难题。你还可以将使用二次电流分布 接口作为电化学电池仿真的第一步，先计算出活化损耗，之后再引入浓度依赖反应动力学。

三次电流分布

三次电流分布用于解释电解质组成和离子强度的变化对电化学过程的影响，以及溶液电阻和电极动力学的影响。为此，它完整求解了 Nernst-Planck 方程（1），借此描述每一种化学物质通过扩散、迁移和对流的质量传输。此外，物质的浓度需要满足电中性假设。电化学反应的动力学表达式解释了活化过电位和浓度过电位，这意味着在电极-电解质界面，反应物的耗尽会导致电解反应的速率受到传输的限制。这也暗示了，电解液中的全部离子和全部活性物质都必须包含在模型中。

与一次和二次电流分布不同的是，三次电流分布中的电解质电流密度不再假定遵循欧姆定律。根据方程式（2），电中性的施加仍然意味着对流通量对电流密度没有贡献，但现在不能忽视电解质浓度变化带来的影响。因此，方程式（2）中的扩散项可能是非零项。

在电极-电解质的界面上，电荷转移反应的电流密度不仅被表示为过电位的函数，也是界面处电活性物质浓度的函数。相对于取决于单电子电荷转移步骤的反应速率，反应动力学方程采用了计算电荷传递电流密度 的 Butler-Volmer 表达式（与方程式（3）对比），在三次电流分布情况下表达式还包含了浓度依赖性。

COMSOL 软件中的三次电流分布 接口求解了电解质电位（）、电极电位（）和一组物质浓度 。根据上述假设，可得到以下方程：

电极： 和

电解质： 和

电解质电中性：

电极与电解质界面：

典型的电流密度表达式：

对于所有参与反应的物质而言，参考浓度 必须是相同的，这确保了过电位在零电流密度（平衡）状态下会遵守热力学 Nernst 方程。

下图展示了线电极示例的三次电流分布情况。由于具有浓度依赖性，三次电流分布会受电解质流动的影响，因此会受到质量传递控制的反应物的影响。当导线之间的流速很小时，为了获得法拉第电流而消耗的电解质不能得到有效补充，从而使电池内的这些部分形成了反应物的耗尽区。这大大降低了局部电流密度，这一现象可描述为“质量传递限制”，它进一步导致更多电流产生于线电极的外边缘。由于电流受到质量传递的限制，因此可以观察到电压降相应地增加，这就是所谓的“浓度过电位”。

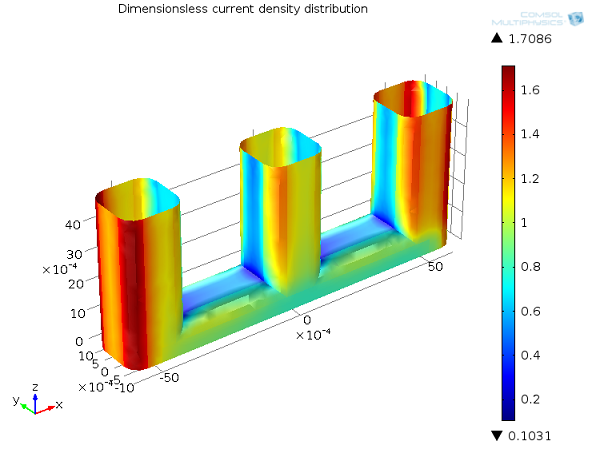
三次电流分布，Ecell = 1.65 V。正极上的电流密度分布（无量纲）。

何时使用三次电流分布 接口？

当电解质混合不均匀或者(与净电流密度相比）浓度相对较低时，可以使用三次电流分布对电池进行模拟，原因是电池内的电解质的组成变化很大，电阻损耗不遵守欧姆定律。在三次电流分布中，利用电流密度和电中性来求解所有 物质浓度的 Nernst-Planck 方程，会使方程组变得非线性和复杂化，致使仿真时间拉长，内存需求增加。在对三次电流分布进行模拟之前，最好利用二次电流分布来预测和判断电化学电池的可能性能。

还有哪些其他选项？

在分析电化学电池的电流-电压关系时，一次、二次和三次电流分布的近似程度依次增加。除此之外，还有其它的建模方法可以最大限度获取有关电池性能的信息，同时尽可能地减少模型的复杂度。

化学物质质量传递和二次电流分布

如果电流密度受到电活性物质质量传递的限制，但电解质组成基本不变，则可能不需要完整求解三次电流分布。相反，离子强度恒定不变意味着我们可以假设电解质溶液服从欧姆定律，具有恒定的电导率，因此可以利用二次电流分布 来求解电解质电位。然而，将动力学速率定律耦合到一个求解化学物质扩散问题的传递模型（必要时也可以求解迁移和对流问题）后，动力学速率定律变得与浓度相关。

事实上，这种耦合方法被用于线电极的三次电流分布案例，这是因为在此案例中是反应物的消耗过程，而非大量电解质物质起到了决定作用。这种耦合方法的另一个应用示例是橙子电池模型。此外，在分析电池和燃料电池时，将电荷传递与质量传递部分耦合是一种普遍的方法。

电分析

当惰性（支持）电解质数量远远超过反应（电活性）物质数量时，就会发生一种特殊情况。因此，与法拉第电流密度相比，溶液的离子强度很大。在这种情况下，电场非常小，因此电解质电位几乎处处相等——电解质溶液电阻对电化学电池的特性没有显著的影响。

当电极动力学（活化）和电活性物质的质量传递的影响远大于电解质溶液电阻的影响时，你可以使用电分析 接口。这个化学物质的传递接口可求解质量传递的对流扩散方程，它包含了电极动力学边界条件，以驱使电极-电解质界面的化学物质通量随局部过电位的变化而变化。

溶液电阻为零的电分析近似适用于电化学技术的标准实验装置，例如循环伏安法、计时安培分析法和电化学阻抗谱。在“案例下载”库中，你可以查看循环伏安法模型的案例，此案例便采用了这种近似方法。

总结思考

本篇博文介绍了 COMSOL Multiphysics 中四个电化学相关模块中都可用的三个电流分布接口，以及何时、为什么要使用它们。COMSOL Multiphysics 软件的强大之处在于，它能够模拟所有电流分布类型（一次、二次和三次），因此在分析电化学电池时，你可以灵活地逐步引入并掌控理论模型的复杂度。

如果你有兴趣使用 COMSOL Multiphysics 来模拟电化学电池设计，或者遇到了本文未提及的问题，请与我们联系。

浏览电化学加载模块

• 电池和燃料电池模块
• 电镀模块
• 腐蚀模块
• 电化学模块

电流分布简介

电化学电池的主要特征表现在电池电流与电池两端电压之间的关系。电流-电压关系取决于不同的物理现象，从根本上影响电池性能。当蓄电池或燃料电池的电流为零（处于平衡状态）时，理论上电压最大，但要想获得电能，就必须产生电流。

当电流通过电池时，电压会发生损耗；相应地，电流密度或许不会均匀分布在电极表面。因此，人们常常通过使电流密度分布均匀化来提高电化学电池（例如电镀电池或蓄电池）的性能和寿命。

相比之下，糟糕的设计会导致电池性能不佳，例如:

• 当实际工作电流通过蓄电池或燃料电池时，电极材料会产生大量损耗，寿命由此缩短
• 电镀过程中涂层厚度不均匀
• 阴极保护系统的表面未受保护

仿真电流分布可以帮助人们更好地了解上述问题，避免此类问题再次发生。

电流分布取决于以下因素：

• 电池几何构造
• 电池工作条件
• 电解质电导率
• 电极动力学（“活化过电位”）
• 反应物的质量传递（“浓度过电位”）
• 电解质离子的质量传递

由于上述复杂性，许多产品应用在建模时会经历适当的简化处理。如果某一个因素主导了电池的性能，其它的因素就不需要考虑在内了。因此，通过一次、二次和三次电流分布的分类，COMSOL 引入了逐次近似方法。

在 COMSOL Multiphysics 中三种电流分布均拥有对应的接口，即一次、二次 和三次电流分布 接口。在对电化学电池进行模拟时，四个针对不同应用的产品模块提供了上述接口，它们是“电池和燃料电池模块”、“电镀模块”、“腐蚀模块”和“电化学模块”。

基本理论

在模拟电化学电池时，必须分别求解电极和电解质中的电位和电流密度。或许还需要考虑做出贡献的物质浓度和涉及的电解（法拉第）反应。

电化学电池中的电极通常是金属导体，所以它们的电流-电压关系遵循欧姆定律：

和电流守恒公式

其中， 表示电极的电流密度矢量（A/m²）， 表示电导率（S/m）， 表示在金属导体（V）中的电势， 表示一般电流源项（A/m³，通常为零）。

电解质是一种离子导体，它的净电流密度可以用所有离子的通量总和来描述:

其中， 表示电解质的电流密度矢量（A/m²）， 表示法拉第常数（C/mol）， 表示物质 的通量（mol/(m²·s)），该物质的电荷数为 。理想电解质溶液中的离子通量可以用 Nernst-Planck 方程来描述，它解释了溶质物质通过扩散、迁移和对流（分别利用三个添加项）的通量：

(1)

其中， 表示离子 的浓度（mol/m³）， 表示扩散系数（m²/s）， 表示迁移率（s·mol/kg）， 表示电解质电位， 表示速度矢量（m/s）。

将 Nernst-Planck 方程代入电流密度表达式后，我们发现：

(2)

同时含有一般电解质电流源项 （A/m³）的电流守恒公式：

除了电极和电解液中的电流守恒之外，您还必须考虑电极和电解质之间的界面，界面上的电流也必须守恒。电流通过两种方式在电极域和电解质域之间进行传递：一是通过电化学反应，此类电流称为电解或法拉电流；二是通过紧邻电极的离子带电双电层的动态充电与放电过程，此类电流称为电容或非法拉第电流。

这种对电化学理论的通用处理方式过于复杂，并不实用。我们可以假设方程（2）中的一个或多个项影响过小，可忽略不计，由此简化并线性化方程。在电化学分析中，三种不同电流分布的应用基于一系列针对一般方程式做出的假设，取决于上文列举的多个影响电流分布的因素的相对影响。在本系列的下一篇文章中，我们将详细讨论假设的内容：从一次、二次到三次分布，假设会依次减少。因此，问题的复杂性增加，但从仿真的详细程度也会相应提高。

下方是线电极建模案例中的几何结构。此案例模拟了电化学电池的一次、二次和三次电流分布。电解质在导线和平坦表面之间的开放内流动。该电化学单元电池可视为一个体积更大的线网格电极中的一个单元，后者是许多大规模工业生产过程中常见的电化学电池装置。

电化学电池的几何结构。两个扁平电极（阴极）之间是线电极（阳极）。左侧是流体入口，右侧是流体出口。顶部和底部平面是惰性的。

下一步：选择正确的电流分布接口

现在，在处理具体的电化学电池仿真模型时，或许您不清楚应该选择三种电流分布接口中的哪一个。在下一篇博客文章中，我们将利用本文中的线电极示例，比较三种电流分布。敬请关注!