电磁学 博客文章
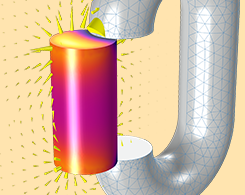
使用 COMSOL Multiphysics® 模拟铁磁材料
欢迎阅读 COMSOL Multiphysics® 铁磁材料建模综合指南,其中包括理论概述与一系列配套动画。

基于 MEMS 技术的应变计仿真设计分析
在土木工程和生物医学领域,应变计用于测量不同物体所承受的形变。通常使用箔式应变计,但灵敏度较低。基于 MEMS 技术的应变计,如双端音叉(double-ended tuning fork,DETF)应变计,可以提供更好的性能。研究人员使用 COMSOL Multiphysics® 软件对一种新型 DETF 应变计的设计进行优化,并将结果与理论模型进行了比较。

使用任意拉格朗日-欧拉方法模拟变形物体
任意拉格朗日-欧拉(ALE)方法在许多模拟应用中被使用。了解帮助创建该方法的数学家,并了解如何在COMSOL Multiphysics®中使用它。

利用射线追踪仿真分析白瞳中阶梯光栅光谱仪
宇航员们常利用中阶梯光栅光谱仪探索遥远太空中的星球。射线追踪软件可以帮助工程师优化白瞳中阶梯光栅光谱仪的灵敏度。
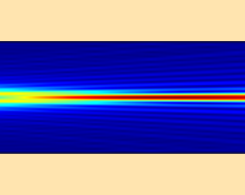
如何使用波束包络法进行波动光学模拟
模拟大型光学系统以一种严格解决麦克斯韦方程的方式是不容易的,由于精细网格的要求。一种解决方案是采用梁包络法。这是如何。
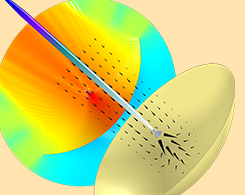
先进天线设计助力空间互联网的开发
如鸟儿展翅,如飞机翱翔,未来的数据共享方式是如此的快捷、自由。环绕地球运行的卫星有可能彻底地改变人类收集与共享信息的方式。相比于有线或无线数据网络,以卫星系统为基础的空间互联网(Internet of Space,简称 IoS)技术能够向全球各地,甚至是最偏远的地区提供网络接入服务。
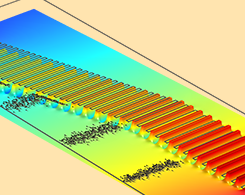
使用 COMSOL Multiphysics® 分析电动离子漏斗
四极滤质器和离子迁移谱仪用于检测爆炸物、研究复杂的生物分子等。 离子漏斗是这些设备的重要组成部分。
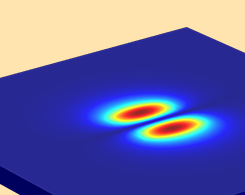
如何使用 COMSOL Multiphysics® 为光学各向异性介质建模
1669 年一个晴朗的夜晚,Erasmus Bartholinus 教授正在把玩一块放在长凳上的冰岛方解石晶体。他突然发现,当方解石覆盖长凳上的文字时,这些文字看起来像一个双重图像。他观察到的这个光学现象称为双折射,是由一束光从晶体中射出时分裂成两个平行光束引起的。我们将在本篇博客中演示这种效应的建模方法。 了解各向异性材料 Erasmus Bartholinus 观察到的穿过晶体的直射光束称为寻常光线,另一种在穿过晶体时发生弯曲的光束,是一种非常光线。从检测有害气体到光子集成电路光束分裂的应用中都广泛存在着各向异性材料,例如上述方解石和长凳实验中的晶体。 穿过各向异性晶体的寻常光线和非常光线。 在物理环境中,当非偏振电磁波束通过各向异性电介质材料传播时,将使得电介质发生极化,产生称为电偶极子 的电荷分布。这种现象导致各向异性电介质材料内出现感应场,其中两种波的折射率不同(寻常波和非常波)。 寻常波在垂直于主平面的方向发生偏振,非常波在平行于主平面的方向发生偏振,其中光轴和晶体中的两个传播方向位于主平面。由于这种特性,波以不同的速度和轨迹传播。 在硅波导中引入各向异性 在之前的一篇博客文章中,我们讨论了由于与 CMOS 制造技术的兼容性,硅及其衍生物二氧化硅如何在光子集成芯片中广泛使用。具有各向同性特性的硅材料用于开发光子集成芯片的原型。然而,由于具有分裂光束和基于偏振的光学效应等光学特性,各向异性材料逐渐显露头角。 在制造波导时的退火过程中,硅光子学中的各向异性偶有显现。由于应力光学效应,纤芯与包层之间的热膨胀差异会导致几何结构失配,从而导致模式分裂和脉冲展宽等效应。各向异性也可以通过改变二氧化硅的孔隙率而有意引入,这样,研究人员能够使用包括二氧化硅(n~1.44)和空气(n~1)在内的一系列有效折射率,从而能够实现非常灵敏的光学传感器应用。 光学传播模式 为了对各向异性介质进行定性分析,研究人员研究了光能如何在平面波导内传播(也称为传播模式)。在平面波导中,我们使用 E^{x}{p,q}和 E^{y}{p,q}(参考文献 2)定义模式,其中 x 和 y 表示偏振方向,p 和 q 表示 x 和 y 坐标中的最大值。 想象一下:你走在一幅 E^{x}{2,1}“风景画”上(如下图所示),“风”(偏振)沿 ±x 方向吹过。从 -x 到 +x 方向行进时,你会遇到两个不同的峰。当你从 -y 方向朝 +y 方向移动时,可以同时观察到两个峰值。 平面波导的模式分析。顶行,从左到右:E^{x}{1,1} 和 E^{y}{1,1}。中间行,从左到右:E^{x}{1,2} 和 E^{y}{1,2}。底行,从左到右: E^{x}{2,1} 和 E^{y}{2,1}。箭头图表示电场; 云图和表面图表示面外功率流(红色表示高幅值,蓝色表示低幅值)。 在 COMSOL Multiphysics® 软件中分析各向异性结构 在使用激光源通过波导发射光束之前,了解哪些光学模式可以在波导的特定芯/包层尺寸内持续存在是非常重要的。使用全矢量有限元工具(例如 COMSOL Multiphysics® 软件)进行模式分析,有助于分别定性和定量地分析光学模式和色散曲线。 引入对角各向异性 对任何各向同性材料进行模态分析都需要定义单个复数值,而对于各向异性材料的情况,需要采用全张量相对介电常数方法。介电常数本质上是电场与材料属性的关系。这里,张量 指的是一个 3 x 3 矩阵,它同时具有对角线(\epsilonxx, \epsilonyy, \epsilonzz)和非对角线(\epsilonxy, \epsilonxz, \epsilonyx, \epsilonyz, \epsilonzx, \epsilonzy)项,如下所示。 \epsilon = \begin {bmatrix} \epsilon{xx}&\epsilon _{xy}&\epsilon _{xz}\ \epsilon _{yx}&\epsilon _{yy}&\epsilon _{yz}\ \epsilon _{zx}&\epsilon _{zy}&\epsilon _{zz} \end{bmatrix} 但是,对于所有材料来说,你可以找到一个坐标系,在这个坐标系中,介电常数张量中只有非零对角线元素,而非对角线元素都为零。这个旋转坐标系中的三个坐标轴是材料的主轴,相应地,介电常数张量中对角线元素的三个值被称为材料的主介电常数。 各向异性晶体主要有两种:单轴晶体和双轴晶体。在选择适当坐标系(其中只有介电常数张量的对角线元素是非零的)的情况下,就光学属性而言,单轴晶体 仅考虑对角线项,即 \epsilonxx = \epsilonyy = (no)2, \epsilonzz […]
