COMSOL 博客

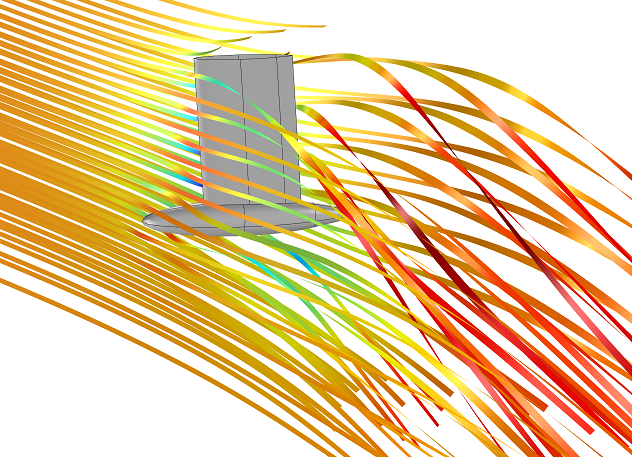
通过 CFD 仿真分析帆船航行的物理原理

在所有类型的船只中，我发现帆船是最迷人的一种，尤其是当帆是唯一的推进方式时。动能从风传递到帆，产生能够平衡阻力并使帆船在水中移动的升力。

石墨烯革命：第四部分

石墨烯可以在高真空下利用热分解制造。为了设计和优化这些高真空系统，工程师可能转向仿真寻求帮助，不过目前还没有多少仿真工具能胜任这一工作。让我们来看一下真空系统如何与石墨烯的生产相关，为什么要模拟它们，以及如何模拟。

非牛顿流体：倒番茄酱的困惑

如果你喜欢吃番茄酱，那么很有可能你已经体验过我们称之为“要么全有要么全无的番茄酱困境”。想象一下，你伸手去拿一个新的番茄酱玻璃瓶，取下瓶盖，把瓶子倒过来时，然后——“什么都没有发生”。直觉上，我们会摇晃或轻拍瓶子，然后——突然你的食物就完全被涂上了番茄酱(当然，除非你的反应真的很好)。在这篇博客文章中，我们将通过仿真模拟瓶子中的番茄酱的流量来演示倾倒番茄酱时的“全有或全无”效果。 我的番茄酱在哪里？ 番茄酱除了是一种特别受欢迎的调味品以外，也是一种非牛顿流体。这是它会出现上述奇怪现象的关键。作为一种非牛顿流体，番茄酱的黏度——以及其流动能力——会随着流体的速度梯度或剪切速率变化。当第一次把番茄酱瓶子倒过来的时候，由于番茄酱的初始黏度很高，很可能你只能得到非常小的流量，如果有的话。好在番茄酱还有一个有趣的剪切稀化特性。当在重力之外施加外力时，增加的剪切力将导致番茄酱的黏度降低，更容易流动。这就是为什么我们有时必须轻拍或摇晃瓶子才能享受番茄酱加薯条。 模拟瓶子中的非牛顿流体流动 为了满足我们的好奇心，以及我们的胃口，并进一步完善我们的番茄酱倾倒技术，我们使用COMSOL Multiphysics 软件和其附加的计算流体力学模块对这个过程进行模拟。在模拟中，我们做了几个简化的假设，包括瓶子的无限延伸(即番茄酱一直都有)和单相层流，忽略了瓶内滞留的空气。所有速度均以米/秒（m/s）为单位。 我们规定了瓶子的几何形状和层流的边界，包括无滑移壁面、压力入口(代表未建模番茄酱部分的重量)和压力出口(外部大气)，如下图所示。 用于模拟的二维几何图形。显示了应用的边界条件。 我们还添加了体积力特性，以包括重力和沿着 y 轴摇晃瓶子 0.2 秒所产生的力。 为了给求解器提供一致的初始条件，重力产生的体积力通过阶跃函数从 0 上升到其最大值(过渡区域为 0.05 秒)。摇动动作是以 0.2 秒宽的矩形函数模拟的。在此期间，体积力加倍。 倾倒番茄酱 我们基于Koocheki 等人的工作，我们先做了一个仿真为之后模拟番茄酱的流动做准备。为了模拟番茄酱的流动，我们使用了非牛顿幂律来表示动力黏度。番茄酱配方通过在幂律方程中指定稠度系数和流动特性指数来模拟。下面的图像显示了添加1%黄原胶的番茄酱配方中较高的初始黏度和非牛顿流动性。 左:以p1(见上面的模型设置)为单位测量的黏度是时间的函数，时间间隔 [0，0.1]秒。右图:以p1(见上面的模型设置)为单位测量的黏度是时间的函数，时间间隔为[0.1，2]秒。番茄酱的剪切稀化特性很明显，尤其是在瓶子摇晃的[1，1.2]秒间隔内。黏度降低，从而允许更多的番茄酱流出瓶子。 左:在三个不同时间沿线 1(见上面的模型设置)测量的黏度。右图:平均出口速度与时间的函数关系。可以看出，番茄酱在重力的作用下慢慢开始流动，然后在摇晃瓶子时容易增加。 左:速度幅度动画从 0.05 到 2 秒。右:1.1 秒时的速度大小。 “番茄酱困境” 等待流速的变化对你来说可能很熟悉。一旦流速开始改变，就会快速变化，导致番茄酱泛滥，覆盖在你的食物上。流速顺其自然地增加导致了剪切力增加，进而降低黏度，导致更高的流速。这就是为什么番茄酱最初似乎是静止的，但后来突然又像水一样流动的原因。 番茄酱从瓶子中流出这个特殊的问题比一开始看起来要复杂得多。有许多变量会影响我们体验一个“绝对的” 番茄酱惊喜。如果你有兴趣进一步研究这种效应，建议你使用 COMSOL Multiphysics 和计算流体力学模块进行模拟实验。例如，你可以研究诸如倾斜角度、瓶子里的空气、甚至瓶子的设计等变量是如何影响番茄酱的倾倒体验的。