网格 博客文章
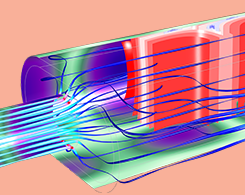
如何在声学仿真中根据频带自动划分网格
想象一下一架优雅的三角钢琴的弧形琴盖。曲线对应于琴弦的长度,琴弦的长度对应于音高的感知。这种视觉感知体现了声学的一个重要元素:我们对音调的感知是基于对数的。这意味着声学现象涉及到较大的频率范围。

COMSOL Multiphysics® 中的网格划分是否并行运行?
网格划分是 COMSOL Multiphysics® 中建模不可或缺的一部分,它会占用大量时间和资源。 并行网格划分通过将域的网格分布在更多内核上来加快速度。
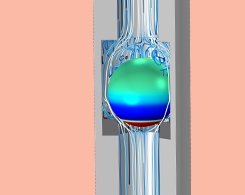
模拟球形止回阀中的流-固耦合作用
在球型止回阀中模拟FSI,找出流量、流体压力和流体速度。COMSOL®软件包含一个预定义的多物理耦合,这使得它很简单。

通过 2 种网格自适应方法实现更高效的计算
网格自适应的目标是通过修改网格实现更高效地求解。通常,我们希望使用尽可能少的网格单元获得精确的解,在不太重要的区域使用较粗的网格,在感兴趣的区域使用较精细的网格。有时,我们甚至可能会考虑各向异性单元。从 5.4 版本开始, COMSOL Multiphysics® 软件包含了一些增强方法以调整网格。这篇博客,让我们来看看如何使用这些方法。 确定所需网格单元的大小 要对网格进行自适应操作,必须知道所需的网格单元大小。然而,找到合适的网格大小并不容易,事实上这需要进行大量的研究。对于稳态和特征值问题,我们可以使用COMSOL Multiphysics 中的 自适应和误差估计 功能基于内置的误差估计自动调整网格。 COMSOL 软件中的网格自适应方法并不局限于使用内置的误差估计,它还具有更高地灵活性。可以先在粗网格上求解一个较简单的问题,然后基于此解通过求解一个表达式来控制较难问题的单元大小。另外,还可以使用导入的插值函数或任何自定义表达式来控制单元大小。 本文不讨论这方面内容,而是假设已经隐式或显式地知道所需的单元大小是 x,y 和 z(三维空间)的函数。也就是说,网格单元的边长由该边中点坐标的函数表达式确定。当然,一般情况下不可能完全满足此要求,即使是一个三角形单元也需要满足三角形不等式。但是,请记住:大小表达式代表空间中每个点所需的单元边长。 根据大小表达式调整网格的 2 种方法 COMSOL Multiphysics 的 网格节点下有 2 种不同的方法可以构建适应大小表达式的网格。 第一种方法,我们可以在网格划分序列中使用大小表达式 属性来改变生成网格的大小。如果使用研究中的网格自适应功能,则相当于选择了 重新生成网格 选项,其中的自由网格生成器(自由三角形网格,自由四边形网格和自由四面体网格)会考虑网格大小。另一方面,例如 映射 、扫掠 和某种程度上的 边界层)会忽略大小表达式属性(根据定义,结构化网格不能遵循大小可变的字段)。简单来说,就是如果我们构建的是结构化网格,可能无法使用此方法。 另一种方法是使用 自适应 操作。此操作通过单元细化和粗化来修改现有网格。我们可以在具有任何单元类型的网格上以及在导入的网格上使用 自适应 操作。这是一种更强大的方法,并且可能更好地遵循指定的大小表达式。但是,结果通常不如从头开始生成的网格平滑。 下面,我们将详细讨论这 2 种方法,并看看二者产生的结果有何不同。 使用大小表达式属性 如前所述,使用大小表达式属性方法通常能获得高质量的网格。但是,如果这种方法产生的单元质量较差(在大小过渡较快时会出现这种情况),则可能无法达到所需的单元大小。有关网格质量的讨论,请阅读博客:如何检查 COMSOL Multiphysics® 中的网格质量。由于每次调整都是从头开始构建网格,因此对于复杂的几何结构而言,此过程可能非常耗时。 使用 大小表达式 属性对一个圆形几何的三角形网格应用大小表达式,得到高质量的网格单元和大小过渡平滑的网格。 如果已知大小表达式(例如,一个全局插值函数),在背景栅格上进行计算通常很方便(上图中的基于栅格计算)。需要确保栅格分辨率足够高,才能捕获大小表达式描述的所有特征。 当大小表达式取决于已知的空间变化量(例如材料),可以使用 初始表达式 计算选项。这样,就可以使用模型中的任何表达式。软件将在求解前计算表达式(与可用于研究步骤的 获取以下步骤的初始值 命令对比)。我们还可以指定某个研究步,因为一些表达式的值取决于研究。 最后,还可以基于现有解计算。内置的 误差 估计使用的是 误差指示器 表达式类型 ,但也可以使用任意的大小表达式,这取决于现有的解决方案。例如,有时可能想在应力较大的地方细化网格。 使用自适应操作 另一种方法是基于现有的网格进行修改来匹配所需的单元大小。这就是 自适应 操作的作用。它适用于所有单元类型,也可作用于导入的网格。它的许多选项和输入字段与 大小表达式 属性相同。 该操作有三种适应方法:最长边细化,常规细化 和 通用修改。前两种细化方法是基于单元边的二等分法操作。由于这些单元边太长,所有现有网格的顶点被保留,因此这些方法无法被粗化。 自 5.4 版本开始,COMSOL Multiphysics 软件内置了 通用修改 方法。顾名思义,就是以非常通用的方式修改网格: 单元可以被细化 […]

使用不连续网格模拟共轭传热
在COMSOL Multiphysics®中,您可以在邻近域使用不同的不连续网格。这种能力非常有用,尤其是在模拟共轭传热问题时。

高效 CFD 仿真的网格划分技术指南
上一篇博客,我们讨论了生成高质量网格的因素以及如何建立 CFD 模型几何结构来进行网格划分。本文,你将了解物理场控制的网格划分,自适应网格细化以及如何在 COMSOL Multiphysics® 软件中使用不同的网格划分技术执行流体流动仿真。

如何在 COMSOL Multiphysics® 中设置网格进行 CFD 分析
计算流体力学(CFD)模型的质量通常由求解问题时所采用的网格质量决定。优质的网格有助于模型收敛、降低内存需求,最终得到精确的解。因此,在求解 CFD 问题时,值得我们投入时间和精力认真创建网格。在本篇博客文章中,我们将介绍影响网格质量的各种因素以及如何准备用于网格划分的流体流动模型的几何结构。

使用任意拉格朗日-欧拉方法模拟变形物体
任意拉格朗日-欧拉(ALE)方法在许多模拟应用中被使用。了解帮助创建该方法的数学家,并了解如何在COMSOL Multiphysics®中使用它。
