结果与可视化 博客文章

如何在 COMSOL Multiphysics 中合并解
在工程分析中,经常需要比较在不同工况下获得的解。可能包括比较不同载荷或参数配置的影响,以及在域的每个点上对解进行包络以找到最差或最佳的情况。对于上述每一种情况以及其他类似情况,我们都需要访问多个数据集。

绘制磁场的空间导数
对于放射学、磁电泳、粒子加速器和地球物理学等领域的应用,计算磁场或磁通量密度的空间导数都很有用。

使用投影算子分析仿真结果
还记得用手在墙上制作皮影戏吗?投影算子,可以用类似的方法分析你的仿真。让我们来解释一下…
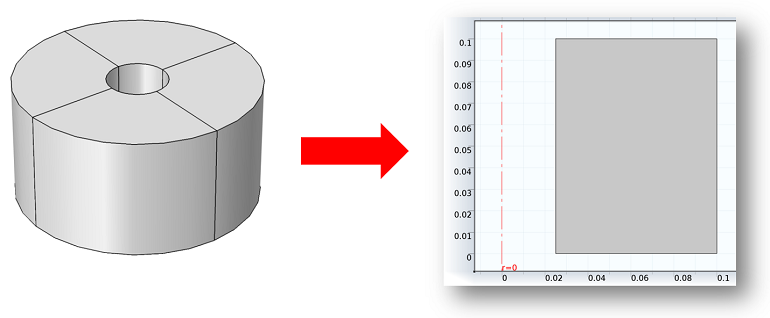
由二维轴对称电磁模型创建可视化三维绘图
今天,我们将介绍在 COMSOL 软件中如何绘制矢量场的三维视图,这些矢量场由 RF 模块和波动光学模块中的电磁波、频域 接口的二维轴对称公式计算获得。 由二维轴对称解生成三维绘图 回想一下,COMSOL 软件中的时谐分析 假设场分量根据 e^{j\omega t} 在时间上振荡,其中 \omega 是角频率。在二维轴对称公式中,电场的角度依赖性由 e^{-j m \phi} 计算,其中 m 是用户指定的整数。由时间和角度的相关性 e^{j(\omega t-m \phi)},可知电场围绕 Z 轴 旋转。我们的目标是由具有这种角度依赖性的二维轴对称解创建三维绘图。 使用二维旋转数据集创建三维绘图 在计算出二维轴对称问题的解之后,COMSOL Multiphysics 会自动生成一个名为“二维旋转”的位于“数据集”节点下的二维数据集,如下图所示。 旋转数据集可用于绘制三维视图。由于我们绘制的是三维绘图,因此将完成一次从 0° 到 360° 的完整旋转。“二维旋转1”的设置如下所示。可以看到,在 “旋转层”下,起始角度被设置为 0,旋转角度被设置为 360。 二维轴对称计算中的平面坐标为 (r,z)。由于角度 \phi 不属于计算域,因此没有被定义。不过,可以通过选中“定义变量”旁的复选框将它添加为三维数据集中的坐标。“二维旋转1”数据集中的角度变量名被设置为“rev1phi”,并可用于下文中的绘图和导出值的表达式中。 如下图所示,考虑一个带矩形截面的轴对称谐振腔。在二维轴对称公式中仅模拟矩形截面。 我们可以使用特征频率研究计算谐振模式。假设我们想绘制 m = 1 模式的场量。下图左侧为在 rz 平面 绘制出的电场大小。我们还可以在将空腔一分为二的表面上绘制电场的大小,这是使用 xy 平面 上的“emw.normE”三维切面图绘制的,平面数被设为 1。右下图中绘制了电场的大小。由于场是围绕 Z 轴 旋转的行波,因此它是轴对称的,这也是因为它遵循 | e^{j(\omega t – m \phi)} | = 1。 绘制电场的径向分量 现在,我们来绘制空腔平面内电场径向分量的实部。具体来说,我们将绘制 t=0 时的 Re { E_r(r,z) \, e^{j(\omega t-m \phi)} },其中 […]

如何执行网格细化研究
几周前,我主持了一场有关 COMSOL Multiphysics 后处理和可视化特征的网络研讨会。这场网络研讨会在 COMSOL 用户中的反响非常好,因此我特意写了本篇博客,希望再次强调下我们所涉及的一个重要专题,即在 COMSOL Multiphysics 中进行网格细化研究。
