结构力学 博客文章
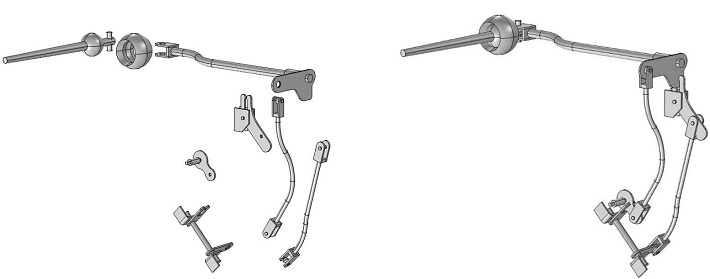
选择第一档:研究老式汽车的换挡原理
跟随我们一起对一辆老爷车的换挡机构进行多体动力学分析。准备上路了吗?

封闭腔体积的求解和控制
在 COMSOL® 软件中,有多种方法可以模拟流体与固体的相互作用。例如,可以使用完整的纳维-斯托克斯方程对压力场和流体速度场进行显式建模。尽管这种方法非常准确,但对于一些流-固耦合问题来说,它的计算成本比实际需要的要高得多。今天这篇文章,我们将介绍一种模拟包含不可压缩流体的封闭腔的方法,假设通过流体的动量和能量传递很小。 编者注: 作者撰写这篇博客的时候,COMSOL 中还没有计算封闭腔中流体载荷的功能。现在,COMSOL Multiphysics® 6.2 版本新增了封闭腔功能,可用于计算封闭腔中的流体载荷。 模拟封闭腔中的流体 我们来看一个 COMSOL 案例库中的示例:超弹性密封条的压缩模型。这个示例考虑的是压缩的软橡胶密封件的横截面。腔体中封闭的流体是空气。该示例计算了压缩力,并将密封件中考虑压缩空气影响与不考虑压缩空气影响的结果进行了比较。 软橡胶密封件的压缩模型。仿真结果显示了应力和应变。使用了不同的方法对密封件内部的空气进行模拟。 示例模型将空气视为可压缩流体,计算了随此二维示例中密封件的横截面积 A 变化的腔体内部压力 p 的变化。接下来,让我们来看看它是如何实现的。将腔体内的空气视为绝热压缩下的理想气体,则压力-密度关系为: \frac{p} {p0}=\left(\frac{\rho} {\rho0} \right)^\gamma=\left(\frac{A0} {A}\right)^\gamma 所以,要计算压力的变化,只需要知道面积的变化就可以了。假设未压缩密封件的面积和压力,以及比热率 \gamma均已知,如何计算横截面积呢?该面积由一个我们甚至不想考虑在模型中的区域来描述。使用高斯定理将面积积分转换为边界积分: A=\int\Omega 1 d\Omega = \int\Omega \left( \nabla \cdot \left[ \begin {array} {c} x \ 0 \end {array} \right]\right) d\Omega = \oint x nx d\Gamma 其中,x 是变形的密封件构型的 x 坐标,n_x 是边界的向外法向量的 x 分量,也在变形配置中,由此给定密封件的封闭区域。这是通过一个定义在封闭体积的完整内部边界上,名为 AreaInt 的积分耦合算子 完成的。变形区域由在“完整模型”上定义的变量 EnclosedArea 定义。 在密封件的内边界上定义面积积分。 分别定义封闭面积和内部压力的变量的定义。必须使用负号来计算面积,因为固体的法线指向腔体。 计算出的变形面积用于确定密封件变形时内部压力的变化。计算得出的压差作为一个载荷施加到密封件内部。要查看上述方法的完整操作,请查看超弹性密封条模型文档。 考虑不可压缩流体 上述方法假设流体是可压缩的,并且密封件的内部压力与面积变化呈函数关系。但如果流体是不可压缩的呢?假设考虑的不是包含可压缩空气的密封件,而是一个充满水的气囊,其中水几乎是不可压缩的。那么,随着结构的变形,封闭的面积不能改变,上述方法就行不通了。因此,我们需要一个替代方案。 我们将 全局方程 功能添加到固体力学接口,通过在这个模型中引入一个额外的方程来求解流体内的压力,使体积不会发生变化。我们来看看这个接口: 引入的全局方程的设置。需要启用高级物理选项才能查看此功能。 上面的屏幕截图显示了用于额外变量 压力 的 全局方程 设置。此方程成立的条件是变量 封闭区域 等于初始面积 123.63 […]

建立子模型:如何分析大型模型中的局部效应
你有没有碰到过对一个具有大量边界条件的特别大的结构进行建模?了解如何使用子模型,这是在COMSOL Multiphysics®中分析大型模型局部效应的一种建模技术。

为什么会有这么多应力和应变?
在结构力学分析中,我们会遇到大量有关应力和应变的定义。它们可能是第二类皮奥拉-基尔霍夫应力(Second Piola-Kirchhoff Stress) 或者对数应变(Logarithmic Strain)。在这篇博客文章中,我们将调查这些数量,讨论为什么需要如此多不同定义的应力和应变,并说明作为有限元分析人员了解这些应力和应变的重要性。
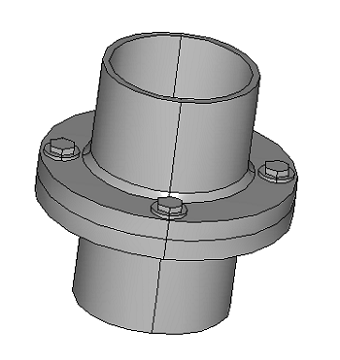
管路连接处预应力螺栓的拉伸应力仿真
在计算拉伸应力之前模拟螺栓预拉伸是一项重要的分析,使用 COMSOL Multiphysics 可轻松进行建模。
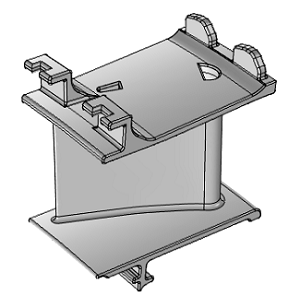
模拟涡轮静叶片的热应力
仿真软件可以帮助我们理解和优化组件设计。任何一个仿真都需要基于实际应用建立模型。建模使我们能够足够详细地表征实际现象,从而获得特定应用或组件的相关信息。
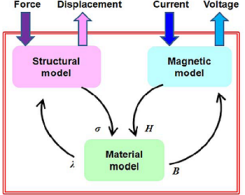
使用 COMSOL Multiphysics® 模拟磁致伸缩效应
如果你曾经站在变压器旁边,可能听到过它发出的嗡嗡声,并怀疑附近是不是有蜜蜂。下次再听到这种声音时,你大可以放心,这不是蜜蜂,而是变压器铁芯的磁致伸缩发出嗡嗡声。 什么是磁致伸缩? 磁致伸缩是一种效应,它会使所有暴露在磁场中的磁性材料的形状发生变化。例如,磁致伸缩效应会使一块铁伸长 0.002%,使镍收缩 0.007%。这一现象曾经因为被用在第一次世界大战期间的声呐设计中而引起了广泛关注。进一步的研究,最终研制出了用于工程的磁致伸缩材料,例如 Terfenol-D,以及最近研制出的 Galfenol,它的伸长率高达 0.04% ~ 0.2%。 磁场引起的应变现象也称为正(磁致伸缩)效应。磁致伸缩效应可以追溯到原子级的相互作用,它是磁性材料中的磁能和机械能在受到磁场和机械应力时所发挥的平衡作用而产生的。下面的动画是对磁致伸缩材料内部情况的简单说明。 当对材料施加交变的磁场时,构成材料的微小椭圆体磁铁会随着磁场大小和方向的变化来回翻转。这些微小磁性体方向的改变表现为一种宏观应变。如果以典型的电力线频率(50Hz – 60Hz)交变磁场,材料中的交变应变会使它像扬声器一样工作,从而产生可以听见的声音。这就解释了变压器发出的嗡嗡声之谜。 这种双向磁机械耦合也会产生逆 效应,即作用在磁性材料上的应力可以通过调整这些微小磁体的方向来改变材料本身的磁性状态。正效应和逆向效应分别用于驱动类和传感类应用。 磁致伸缩材料的应用 从航空航天、石油生产到声学和 MEMS,磁致伸缩材料几乎可以应用在所有行业。下面列出了一些重要的商业应用: 声学设备 声呐 水听器 用于清洗、混合和乳化的超声波振动器 超声波摩擦焊接 驱动器 直线电机和旋转电机 尺蠖式驱动器 用于机床头部的位置控制器 燃油喷射系统 光学扫描系统 液压驱动器,例如伺服阀和泵 用于减小阻力的智能机翼中的主动后缘 传感器 位置传感器 非接触式扭矩传感器 磁场传感器 MEMS生物和化学传感器 振动控制 减振器 平台稳定器 图像稳定器 能量收集器 混合智能结构 带混合压电/磁致伸缩磁芯的 Tonpilz 换能器 混合压电/磁致伸缩复合驱动器和传感器 您还可以利用磁致伸缩效应把家里客厅的墙壁或窗户变成扬声器! 那么,如何在 COMSOL Multiphysics 中对这种有趣的现象进行建模呢? 在 COMSOL Multiphysics 中对磁致伸缩进行建模 对磁致伸缩型换能器进行建模的正确方法包括准确模拟磁和结构性能,并使用适当的材料模型模拟这些物理场之间的相互作用。COMSOL 中内置了预定义的物理场接口,可用于设置磁仿真和结构仿真。COMSOL 还支持灵活地设置用户自定义的本构关系,用数学的方式表示材料模型。 实验表明,正向和逆向磁致伸缩效应都是非线性的。当模拟那些在准静态条件下运行,但暴露在大范围机械力和磁场中设备时,建立完整的非线性响应模型可能很重要。在这类设备中,了解磁致伸缩磁芯在什么工作条件下饱和是有用的。这些信息可以为设计人员提供极限值,还可以解释实际的非线性行为,例如传感器灵敏度的变化或用户期望从磁致伸缩设备获得的驱动器最大力。 在某些已知频率和已知工作条件下工作的声学换能器中,可以使用线性本构定律简化材料模型。这些定律(或方程)是在假设换能器操作涉及围绕偏置点的小幅振荡的条件下推导的。而如果在建模方法中考虑这些实际因素,那么我们就能够轻松模拟磁致伸缩换能器在较宽工作频率范围内的响应。 在 COMSOL Multiphysics 中,可以同时设置非线性和线性本构方程模拟磁致伸缩器件。接下来,我想与大家分享一些我们对一个实验换能器进行模拟的结果。 模拟磁致伸缩换能器 典型的换能器有一个被驱动线圈包围的磁致伸缩磁芯。流过线圈的电流会产生磁场。传感器有一个钢制外壳,包围着驱动线圈和铁芯。磁芯连接到活塞上,活塞用于在启动器配置中将磁芯的位移传递到外部机械部件上,或在传感器配置中将负载从外部机械或声源传递到磁芯上。钢制外壳、活塞和铁芯形成了一个封闭的磁通路径。 对于非线性模型,我们使用了 Galfenol的典型材料表征曲线,并确定了重要设计参数的非线性,例如换能器的阻力。我们还能够探索驱动和传感行为的变化与各种磁场和作用在传感器上的拉伸和压缩载荷的函数关系。有关这个模型的更多信息,请查看 COMSOL 案例库中的非线性磁致伸缩换能器和传感器 教程案例。 非线性磁致伸缩换能器仿真中的位移幅度、驱动器和传感器曲线以及换能器阻力图。 对于线性模型,我们使用了 Terfenol-D 的典型材料参数,并生成了驱动器载荷线。我们还研究了换能器位移的幅度和相位,以及驱动线圈阻抗的频率响应。 线性磁致伸缩传感器仿真中的驱动器载荷线、线圈阻抗、位移幅度和位移相位图。 2013 年 COMSOL […]
使用临界面法预测疲劳
对疲劳的研究始于 19 世纪,起因是铁路车轴发生故障从而导致了火车事故。在旋转轴中,应力的变化是从拉伸到压缩,再回到拉伸,由于应力状态是单轴和成比例的,因此载荷历程很简单。
