在 COMSOL 中如何正确模拟流动

许多工程应用问题都涉及流体流动，除了代替风洞实验的经典 CFD 仿真，电子设备冷却或化工行业中由流体输送反应物引起的流动都必须考虑。COMSOL Multiphysics 提供了可以模拟各种流动类型的专用的接口。那么，什么时候应该使用层流或湍流接口呢？

“千禧年大奖难题”之一：理解流动的本质

流动的性质非常复杂，在数值上求解其控制方程——纳维-斯托克斯方程具有一定的挑战性。

据报道，英国应用数学家 Horace Lamb 曾经说过：“我现在已经是个老年人了，当我死后去了天堂，有两个问题我希望能得到启发。一个是量子电动力学，另一个是流体的湍流运动。对于前者，我真的相当乐观。”

也许他很幸运，在天堂也得到了后一个问题的答案，但在地球上，这仍是克雷数学研究所的一个“千禧年大奖难题”。如果您能证明纳维-斯托克斯方程在三个维度上有解并且该解没有奇点，就可以获得 100 万美元的奖励。这个证明可以帮助我们理解湍流的性质，这仍然是 CFD 仿真中的最大挑战。

当然，大自然总是有答案的。在天空中的云层、大海中的波浪和锅中的沸水中，我们都可以发现湍流现象。但是，我们还是希望为我们的应用找到一个数值解，从而预测和优化应用的性能。COMSOL Multiphysics 软件内置了许多接口，可以求解由纳维-斯托克斯方程推导的方程，并且适用于不同的流动类型。

在这篇博客中，我们将对适合使用层流和湍流接口表征的具有不同特性的流动类型进行说明。

表征流动

选择维度之后，模拟流动首先要考虑的是：是否需要考虑温度变化。这决定了您是选择非等温流动接口求解纳维-斯托克斯方程和传热方程，还是忽略温度变化只求解纳维-斯托克斯方程。这听起来很容易。但是，现在要你决定是否需要选择一个湍流接口，或者使用层流方法是否够用，这并不容易。

雷诺数和流动状态

技术类应用主要涉及强制流动。在这类流动中，流体由泵或风扇等外部源驱动，并以一定速度进入模拟域。无量纲数有助于在仿真开始前对流动有一个大致的了解。雷诺数是表征流态的无量纲数，它描述的是惯性与黏性力的比值：

其中，\rho是密度，U是特征速度，d是特征长度尺度，\mu是动力黏度。在这里，您可以看到\mathrm{Re}并没有明确定义。特征速度和长度尺度是什么？如果材料特性取决于温度会怎样？

在雷诺数非常低的情况下，\mathrm{Re}\ll1，黏性力支配惯性力。因此，后者在纳维-斯托克斯方程中可以忽略。对于这种流动，可以使用COMSOL Multiphysics 中的蠕动流接口。或者，如果您的应用是非等温流，可以激活相关设置窗口中的“忽略惯性项（斯托克斯流）”复选框。

当雷诺数较高，但低于某个临界值\mathrm{Re}_c（临界雷诺数）时，流动是层流。雷诺数大于\mathrm{Re}_c时，流动是湍流。对于不同的情况，\mathrm{Re}_c的值必须通过实验设置或数值实验手动确定。幸运的是，对于一些标准的工程应用，这些已经得到确定，我们可以直接参考相关文献。但是，即使你已经在文献中找到了\mathrm{Re}_c的值，层流到湍流的过渡并不是立即发生的，并且有两种状态都存在的过渡区。

在这种情况下，我们应该采用哪种方法：层流还是湍流？

瑞利数和自然对流

在自然对流中，流动是由浮力驱动的。通常情况下，浮力是由于温度差异而产生的，但浓度梯度也可能是驱动机制。自然对流在地球科学中发挥着重要的作用。在地球的外核，自然对流产生地球的磁场，在大气层中，它决定了地球上的气候。

由于自然对流（例如在建筑物理学或电子设备中）引起的冷却通常使用传热系数进行建模，传热系数是通过实验或数值计算确定的。对于自然对流仿真，我们总是需要耦合传热和流动接口才能实现。因此，非等温流接口是一个不错的选择。

表征自然对流的无量纲数称为瑞利数，它是格拉晓夫数\mathrm{Gr}和普朗特数\mathrm{Pr}的乘积，其中格拉晓夫数表征的是浮升力和黏性力的比值，普朗特数表征的是动量扩散和热量扩散的比值。

式中，\alpha是热膨胀系数，\Delta T是温差，d在这里是指处于活动状态的浮力层的高度。与雷诺数相似，这里也有一个临界瑞利数\mathrm{Ra}_c。\mathrm{Ra}<\mathrm{Ra}_c，它代表热量只能通过传导传递。当\mathrm{Ra}=\mathrm{Ra}_c时，表示对流是稳定层流状态中的主要传热过程。随着瑞利数的增加，稳定流逐渐变得不稳定，最后变为湍流。

不同配置下的流动状态

现在，我们来讨论几种不同的流动状态，以及 COMSOL 中适合表征每种流态的接口和研究类型。

1. 圆柱体周围的流动

随着雷诺数的增加，这种流动类型会形成卡门涡街，这是一个无温度变化的 CFD 验证的基准示例。使用圆柱体的直径作为计算圆柱体周围流动的雷诺数的特征长度，材料属性是常数（对于其他障碍物也是如此）。当雷诺数处于较大的范围内时，障碍物后面的流场会形成周期性的漩涡，如下图所示。

\mathrm{Re}\approx 2时的稳态速度场。此时的流动是真正的层流并且有稳态解。这种流动可以通过层流接口和稳态研究来求解。

时间为7s，\mathrm{Re}\approx 100时，的瞬态速度场。速度场随空间和时间变化。在合适的网格和时间步长下，可以使用层流接口和瞬态研究来求解这种流动。

随着雷诺数的进一步增加，涡流的频率将增大并最终导致湍流发生。特别是在过渡状态中，会出现3D 不稳定性并且必须通过 3D 层流接口来求解。一旦流动变成完全湍流，就可以切换回 2D 并使用湍流接口求解。

2. 管壳式换热器

管壳式换热器是一种常见的换热器，并且是非等温流动与强制对流的一个典型例子。在这个应用中，水经过管侧流动，空气经过换热器的壳侧流动。这两种材料的特性都与温度相关，在计算雷诺数时需要考虑这些特性。管内部的特征长度为管的直径，但入口和出口区域的特征长度未知。

同样，管道和挡板周围的空气流动的特征长度同样也不明确。管道和挡板引导空气流动，从而增加了两种流体之间的热量传递。您可以参考相关文献，例如这个资源，来查找具有较好的\mathrm{Re}估计值的示例。

观察雷诺数如何在模拟域中变化非常有意思。在 COMSOL Multiphysics 中，您可以在模拟完成后绘制\mathrm{Re}。为此，您可以水域添加一个 3D 体积图，并在表达式栏中输入 nitf.U*nitf.rho*0.015[m]/nitf.mu。然后，对基于局部速度、密度和黏度的每个点，以管道直径作为特征长度计算雷诺数。在此长度尺度适用的情况下，雷诺数超过管道内流动的临界值，并且足以使流动成为湍流。

对于这个示例，我们使用湍流接口进行稳态研究。这表示我们并不求解所有可能出现的与空间和时间相关的涡流特性。相反，我们通过添加额外的变量，来考虑涡流对热交换器特性的影响，计算一个平均速度场。

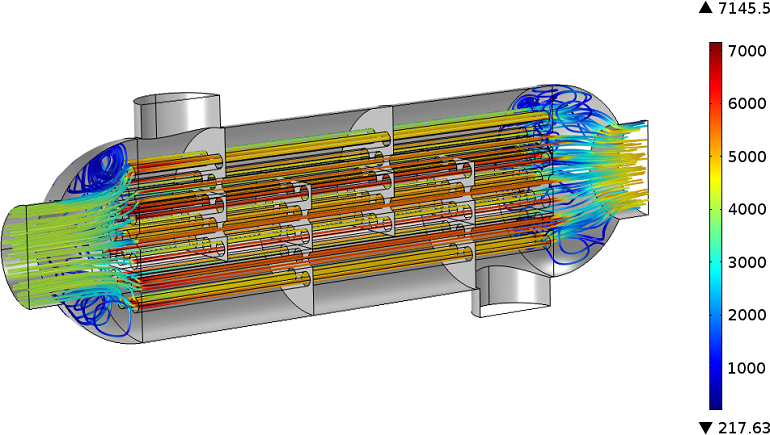
管侧速度场的流线图。颜色标尺表示雷诺数。

3. 球壳中的自然对流

最后一个例子属于地球物理学主题，是关于一个球壳（无旋转）内浮力驱动的自然对流问题。当对流开始时，首先形成一些稳态对流单元（瑞利-贝纳尔单元）使浮力增加，进而引起单元开始移动。最后，这些单元破裂后产生更小的涡流，在较短的时间尺度上支配流动系统并产生湍流。

下面的动画演示了球壳内的自然对流，其中浮力作用在径向方向。纳维-斯托克斯方程是用无量纲参数而不是材料属性定义的，浮力则用瑞利数表示。该模型是使用一个含瞬态研究的层流接口来求解的。

从线性温度分布开始，浮力首先形成对称对流单元，但很快就获得了 Ra = 250 的非对称速度和温度分布。

结论

通过研究几种不同的流态，我们得出以下结论：选择哪种流动接口并不总是很明确。如果无量纲数\mathrm{Re}或\mathrm{Ra}明显小于或大于其配置的临界值，那么选择哪个接口很明确。

对于经常出现在微流体设备中的完全层流，您可以选择层流接口。如果\mathrm{Re}\ll 1，您应该选择蠕动流接口。

许多工业应用都具有高流速和高雷诺数，对于这种情况，需要选择湍流接口。阅读我们之前的博客，详细了解您应该选择哪种湍流模型。

毕竟，CFD 仿真有一定的困难，因为我们还没有完全弄清楚流动的性质。COMSOL 软件提供了使用最新数值技术模拟所有流动状态的接口。下列 COMSOL 案例库中的示例模型可以帮助您了解哪种接口适合您的应用。

下载模型

• 包含层流的自然对流：
  • 保温瓶的自然对流冷却
• 层流自然对流：
  • 自由流体中的浮力流
    • 包含对无量纲参数及其对热行为的影响的详细说明
• 考虑含湍流的自然对流和强制对流：
  • 房间内的置换通风
• 通过 90 度弯管的湍流：
  • 管道弯头中的流动