COMSOL 博客

电热耦合分析中常见的误区

作者 Walter Frei

2018年 4月 17日

在电力传输和消费电子等应用中，模拟温度非线性材料的电磁热可能至关重要，其中非线性是指材料的电导率和热导率随温度变化。在对这些非线性进行建模时，由于涉及非线性材料属性、边界条件和几何结构的组合，即使是经验丰富的分析人员有时也会得到非常意想不到的结果。这篇博客，让我们通过一个非常简单的例子来找出其中的原因。

了解欧姆定律和电阻热

作为工程技术人员，我们最先学习的一个物理定律就是欧姆定律：通过一个器件的电流等于施加的电压差除以器件电阻，或 I = V/R_e，其中电阻 R_e是器件几何结构和材料电导率的函数。

在学习该定律后不久，我们可能还学习了器件内的耗散功率等于电流乘以电压差，或 Q = IV，也可以写为 Q = I²R_e 或 Q = V²/R_e。也许稍后在我们的研究中，还会了解热导率和等效器件热阻 R_t，这样，我们可以从集总意义上通过 ΔT = QR_t计算器件相对于环境条件的温升，然后可以使用 T = T_{ambient} + QR_t 确定绝对器件温度。

我们从这一点开始讨论，考虑一个完全集总的器件模型。（是的，一开始非常简单，这部分甚至不需要使用 COMSOL Multiphysics® 软件！）假设有一个电阻 R_e=1 Ω、热阻 R_t = 1 K/W 的集总器件。用恒定电压驱动它，并计算温度，T = T_{ambient} + (V^2 / R_e) R_t，或者通过峰值温度为 T = T_{ambient} + I^2 R_e R_t的恒定电流驱动它。

我们选择的环境温度为 300 K 或 27°C，大约是室温。现在，我们绘制器件集总温度随电压（从 0 到 10 V）和电流（从 0 到 10 A）增加而变化的情况，如下图所示。不出所料，我们看到温度呈二次曲线规律升高。

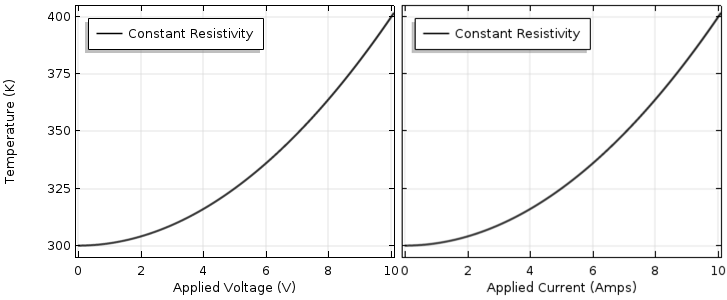
并排图显示温度随外加电压和电流变化的情况。
假设材料属性恒定，器件温度随外加电压（左）和外加电流（右）变化。

这条曲线可以用来预测更大范围的操作条件。假设我们想要将器件驱动至其失效温度700 K（427°C），在此温度下，材料会熔化或蒸发。根据这条曲线，通过一些简单的数学运算将得到最大电压为 20 V，最大电流为 20 A，但这完全是错误的！

将材料非线性引入简单集总模型

此时，你可能已经准备好指出我们犯的一个简单错误：在温度变化的情况下，电阻不是恒定的。对于大多数金属，电导率随着温度的升高而下降，由于电阻率与电导率相反，器件电阻率上升。因此，我们引入电阻率与温度的关系：

R_e = \rho_0(1+\alpha_e(T-T^e_0))

这被称为线性化电阻率模型，其中，ρ₀是参考温度 T^e_0 下的参考电阻率，α_e是电阻率的温度系数。

我们选择 ρ₀ = 1 Ω，T^e_0 = 300 K，α_e = 1/200 K。现在，当器件温度为 300 K 时，电阻为 1 Ω，当器件温度比设定温度高 200 K 时，电阻为 2 Ω。集总温度随电压和电流变化的方程现在变成：

T = T_{ambient} + (V^2 /\rho_0(1+\alpha_e(T-T^e_0))) R_t

和

T = T_

{ambient} + I^2 \rho_0(1+\alpha_e(T-T^e_0)) R_t

这些方程稍微复杂一点（第一个是用 T 表示的二次方程），但仍然可以手工求解。温度随电压和电流增加而变化的图如下所示。

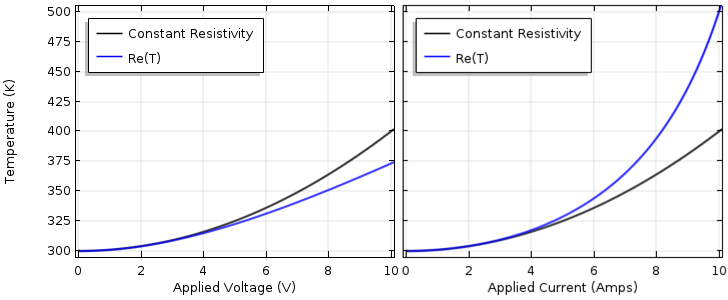
并排图表绘制了电热分析的温度和电阻率。
器件温度随外加电压（左）和外加电流（右）的变化以及电阻率随温度的变化。

对于电压驱动的问题，随着温度升高，电阻也会升高。由于电阻出现在温度表达式的分母中，更高的电阻得到更低的温度，我们看到温度将低于恒定电阻率情况下的温度。如果我们用恒定电流驱动器件，分子中会出现与温度相关的电阻。当我们增加电流时，电阻热将高于线性材料。

此时，我们尝试计算该器件能够承受的最大电压或电流，但你可能已经意识到我们已经犯下的第二个错误：我们还需要考虑热阻的温度依存性。对于金属，我们可以合理地假设电导率和热导率呈现相同的趋势。因此，使用一个类似于我们之前使用的非线性表达式：

R_t = r_0(1+\alpha_t(T-T^t_0))

现在，电压驱动和电流驱动温度方程变为：

T = T_{ambient}
+ V^2 r_0(1+\alpha_t(T-T^t_0))/\rho_0(1+\alpha_e(T-T^e_0))

和

T = T_

{ambient}
+ I^2 \rho_0(1+\alpha_e(T-T^e_0))/r_0(1+\alpha_t(T-T^t_0))

尽管与以前略有不同，但这些非线性方程现在相当难以求解。仿真软件开始变得更具吸引力！求解出这些方程后（我们设置 r₀ = 1 K/W、α_t = 1/400 K、T^t_0 = 300 K），可以绘制器件温度，如下所示。

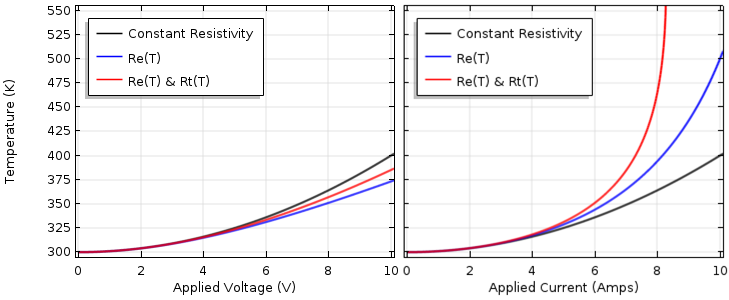
两个曲表显示电阻率和热阻率随温度的变化，温度是电压和电流的函数。
器件温度随外加电压（左）和外加电流（右）的变化以及电阻和热阻随温度的变化。

注意，对于电流驱动的情况，温度渐进地上升。由于电阻和热阻都随着温度的升高而增加，因此器件温度随着电流的增加而急剧升高。随着温度上升到无穷大，这个问题变得无法求解。实际上这完全是预料之中的; 事实上，这就是汽车保险丝的基本工作原理。现在，如果我们在 COMSOL Multiphysics 中求解这个问题，也可以将它作为一个瞬态模型（包含由于器件密度和比热引起的热质量）来求解，并预测器件温度升至其失效点所需的时间。

幸好电压驱动的情况要简单一些。这里，我们也看到了一种可预测的现象：与只考虑与温度相关的电导率时相比，热阻率的上升会使温度升高。现在，有趣的一点是温度仍低于恒定电阻率的情况。这有时也会让人困惑，但请记住，其中一个非线性因素会降低温度，另一个会升高温度。一般来说，对于更复杂的模型（比如你将在 COMSOL Multiphysics 中构建的模型），你不知道哪个非线性因素将占主导地位。

在这里还会犯什么错误？我们使用了热阻率的正温度系数。对于大多数金属来说，这当然是正确的，但事实证明，对一些绝缘体来说，情况正好相反，玻璃就是一个常见的例子。通常，器件总热阻主要是绝缘体的函数，而不是导电域的函数。此外，器件的热阻应包括冷却对周围环境的影响。因此，自由对流（随温差增加）和辐射（对温差具有四阶依赖性）的影响也可以集中到这个单一的热阻中。不过，现在，我们保持问题（相对）简单，只需切换热电阻率温度系数 α_t = -1/400 K 的符号，并直接比较驱动电压高达 100 V 与驱动电流高达 100 A 的电压驱动和电流驱动情况。

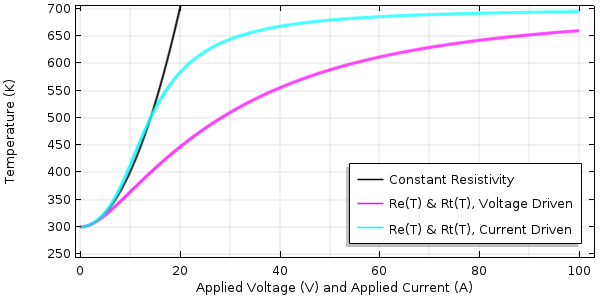
不同条件下器件温度的 COMSOL Multiphysics® 绘图。
热电阻率温度系数为负的情况下器件温度随外加电压（粉色）和外加电流（蓝色）变化的情况。

我们现在看到一些截然不同的结果。可以看出，对于电压和电流驱动的情况，温度在低负载下大致呈二次方升高趋势，但在较高负载下，由于热阻降低，温度升高开始趋于平缓。斜率虽然总是正的，但幅度减小了。电流驱动的情况开始渐进地接近 T = 700 K，但电压驱动的情况一直显著低于失效温度。

这是一个重要的结果，也凸显了另一个常见错误。这里我们用于电阻和热阻的非线性材料模型是近似值，如果接近 700 K，这些近似值就开始失效。如果我们预期在这种情况下运行，我们应该回到文献中，找到更复杂的材料模型。虽然现有的非线性材料模型确实解决了问题，但总是需要检查它们在计算的工作温度下是否仍然有效。当然，如果不接近这些操作条件，我们可以使用线性化电阻率模型（COMSOL Multiphysics 中的内置材料模型之一）。这样我们的模型将是有效的。

现在可以从所有这些数据中看出，温度与驱动电压或电流的关系非常复杂。当考虑非线性材料时，温度可能高于或低于使用恒定属性时的温度，温度响应的斜率可以仅根据操作条件从非常陡峭变为非常平缓。

这些结果让你彻底困惑了吗？如果改变阻力表达式中的一个系数会是什么情况呢？某些材料的电阻率和热阻率温度系数为负，如果使用更复杂的非线性模型呢？即使是在这种简单的集总器件情况下，你有信心说出关于预期温度变化的信息，还是更愿意根据严格的计算来确认？

电热分析中常见误区的总结性思考

真实世界中器件的情况如何？包含许多不同材料？不同的电导率和热导率随温度变化？形状复杂吗？你会仅在稳态条件下或在时域中模拟这种情况来了解温度升高需要多长时间吗？也许（实际上很可能）还会包含非线性边界条件，例如辐射和自由对流。我们不想通过单一集总热阻来近似，你呢？如果几乎什么都有！你将如何进行分析？当然要使用 COMSOL Multiphysics！