
“工欲善其事,必先利其器”。在进行高频电磁仿真时,选择适合的接口是十分重要的。在这篇博客文章中,我们以空气中平面波入射到介电板为例,使用了两种不同的方法对其进行求解,并根据仿真结果阐释电磁波,频域接口与电磁波,波束包络接口在实际应用中的差异和各自的优势。
在两个电磁接口中对自由空间剖分网格
上文的两个接口均可求解频域麦克斯韦方程,但二者的实现方式略有不同。电磁波,频域接口在 RF 模块和“波动光学”模块中都能打开,可用于直接求解仿真模型中各处的复杂电场。而电磁波,波束包络接口只能从“波动光学模块”打开,可求解给定波矢的电场复包络。在下文中,我们将电磁波,频域接口简称为全波仿真,将电磁波,波束包络接口简称为波束包络仿真。
为了了解全波仿真与波束包络仿真之间的区别,我们首先来讨论一个普通示例:在自由空间内传播的平面波(如下图所示),然后我们会将从示例中学到的知识应用到介电板案例中。
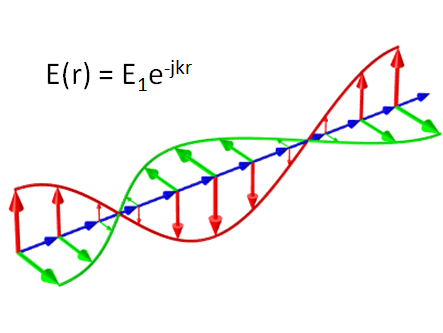
原理图展示了在自由空间内传播的平面波,其中红色、绿色和蓝色分别表示电场、磁场和波印廷矢量。
要正确计算全波仿真结果的谐波性质,所使用的网格必须比场内的振荡更加精细。两篇关于求解电磁波问题和模拟相关材料的博客文章对仿真工具的话题进行了深入探讨。对于全波仿真而言,为了模拟平面波在自由空间中的传播,网格单元的数量需要随研究的自由空间域的大小而变化,那么波束包络仿真是什么情况呢?
波束包络方法尤其适用于那些波矢\mathbf{k}为已知量的模型。从实践的角度来看,这意味着我们要使用拟设\mathbf{E}\left(\mathbf{r}\right) = \mathbf{E_1}\left(\mathbf{r}\right)e^{-j\mathbf{k_1}\cdot\mathbf{r}}对场进行求解。请注意,拟设中唯一的未知量是包络函数\mathbf{E_1}\left(\mathbf{r}\right)。正是因为要对包络函数剖分网格才能获取完整的解,所以软件才会将这个接口命名为波束包络。在自由空间中的平面波案例中,拟设的形式与解析解完全吻合。我们知道包络函数通常是一个常数,如下图中绿线所示,所以我们到底需要多少网格单元才能对解进行解析呢?答案是只要一个。
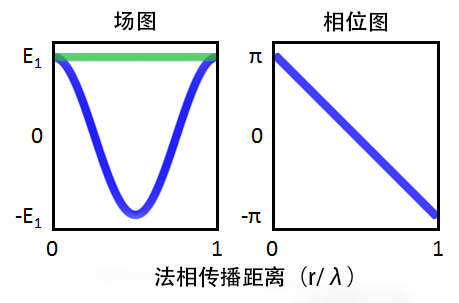
在自由空间中传播的平面波的电场和相位。在场图中(左图),蓝线和绿线分别表示 E(r) 的实部abs(\mathbf{E_1}\left(\mathbf{r}\right)e^{-j\mathbf{k_1}\cdot\mathbf{r}}) = E_1和绝对值real(\mathbf{E_1}\left(\mathbf{r}\right)e^{-j\mathbf{k_1}\cdot\mathbf{r}}) = E_1\cos(kr)。相位图(右图)显示了 E(r) 的变元。在两幅绘图中,x轴表示归一化的波长,代表电磁波的一次完整振荡。
在实际应用中,波束包络仿真比刚刚使用的拟设\mathbf{E}\left(\mathbf{r}\right) = \mathbf{E_1}\left(\mathbf{r}\right)e^{-j\mathbf{k_1}\cdot\mathbf{r}}更加灵活,原因有两个:一是我们可以指定用户自定义的相函数\phi\left(\mathbf{r}\right) = \mathbf{k}\cdot\mathbf{r},而不必指定波矢;二是仿真中的双向选项允许波进行第二次传播,并可以使用完整的拟设\mathbf{E}\left(\mathbf{r}\right) = \mathbf{E_1}\left(\mathbf{r}\right)e^{-j\phi_1\left(\mathbf{r}\right)} + \mathbf{E_2}\left(\mathbf{r}\right)e^{-j\phi_2\left(\mathbf{r}\right)}。我们将在介电板(也称法布里-珀罗干涉仪)建模案例中应用双向选项功能。
在介电板案例中,我们将再次强调本节中讨论的要点,以便于您更清楚地理解。全波仿真直接求解整个物理场,因此其网格单元尺寸与波长成正比,另一方面,波束包络仿真求解的是给特定相位/波矢的包络函数,因此其网格单元尺寸不受波长的影响。如果波束包络仿真能够取代全波仿真执行求解工作,就能大幅减少大型结构使用的网格单元数量,不过前提是您已经预先了解了仿真模型中各处的波矢(或相函数)。由于自由度、内存占用和仿真时间全部取决于网格单元的数量,所以仿真工具的选择会对仿真的计算要求产生巨大的影响。
在 COMSOL Multiphysics 中对电介质板剖分网格
通过下图中的二维几何图示,我们可以清楚地看到多种不同的波,这些波都是我们需要在平面波入射电介质板的仿真中考虑的。在条形板左侧,我们需考虑向右传播的入射波和向左传播的反射波。因为反射发生在电介质板内部,故不得不考虑在板内向左和向右传播的波,以及右侧的透射波。接下来我们还要选定具体的案例以便使用确定的数值。
假设电介质板是厚度为 525 µm 的无掺杂硅(Si)晶片,接下来我们将要模拟太赫兹(THz)辐射的响应(即亚毫米波)。太赫兹辐射包含约 1 mm 至 100 µm 的波长,近来越来越多地被用于控制半导体的特性类型。在这个范围内,无掺杂硅的折射率为常数 n = 3.42。我们将传播方向上的域长度设为 15 mm。
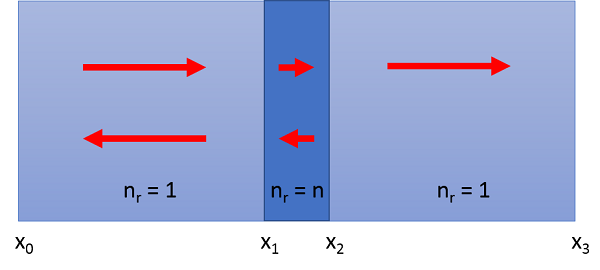
仿真几何图示。红色箭头表示入射波和反射波。左侧和右侧区域表示折射率 n = 1 的空气,位于中心的硅制板的折射率 n = 3.42。底部的 xis 表示平面的空间位置。条形板位于仿真域的中心,因此 x1= (15 mm – 525 µm)/2。请注意,此图像并未按照实际比例绘制。
针对二维全波仿真,我们将最大单元尺寸设为\lambda/8n,以确保对解进行良好的解析。仿真在y方向上保持不变,因此将仿真模型的高度设为\lambda/(8\times3.42)。由于我们已限制了波沿x轴的传播,因此可通过选择映射网格来生成矩形单元。这样一来,网格在y方向上等于一个网格单元的厚度,在x方向上的网格单元尺寸则为\lambda/8n,其中 n 的数值取决于网格是在空气中还是在硅制板中。再次提醒,此仿真的网格会随波长变化。
在建立波束包络仿真的网格之前,首先须指定自定义相函数。“案例下载”中的高斯光束以 Brewster 角入射案例演示了如何通过使用变量来定义每个域的用户定义相函数,我们将在此使用相同的技巧。参照上方几何图形中的 x0,x1和 x2,针对三个域内从左向右传播的平面波,我们将其相函数分别定义为
其中 n = 3.42,表达式的第一行对应最左侧域中的\phi,第二行对应硅制板中的\phi,最后一行对应最右侧域中的\phi。然后我们将该变量应用于第一个波的相位,将该变量的负值应用于第二个波的相位。由于我们完整地捕捉了拟设中解的完整相位变化,所以整个模型可以使用只包含三个单元的映射网格——每个单元对应一个域。接下来让我们研究一下波长等于 1 mm 和 250 µm 时,两个接口各自的硅制板域的网格图像。
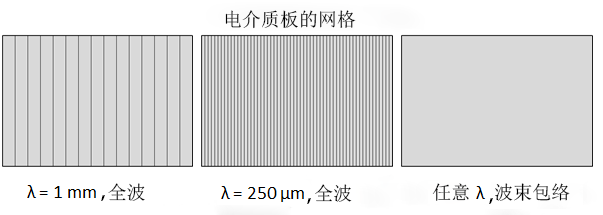
硅制(电介质)板的网格。从左到右依次为:波长等于 1 mm 时的全波网格,波长等于 250 µm 时的全波网格,任意波长下的波束包络网格。请注意,全波网格的密度明显随波长的减小而增大,与此同时,不论波长如何变化,波束包络网格始终是单个矩形单元。
没错,以上就是波束包络仿真中硅制板域的正确网格。因为拟设与解完全匹配,整个仿真模型总共只需使用三个单元:一个单元用于硅制板,两侧的空气区域各使用一个单元。网格单元不受波长影响。另一方面,\lambda= 250 µm 时全波仿真的网格的密度约为\lambda= 1 mm 时的五倍。我们来看一看这些仿真中所求解的自由度(degrees of freedom,简称 DOF)的具体数量。
| 模拟波长 | 全波仿真 使用的自由度 |
波束-包络仿真 使用的自由度 |
|---|---|---|
| 1 mm | 4,134 | 74 |
| 250 µm | 16,444 | 74 |
全波和波束包络仿真在不同波长下对应的自由度数量。
至此,我必须再次说明,这样的对比并不意味着两个接口具有优劣之分。二者仅是使用的技术不同,选择合适的方法对于仿真来说极为重要。不过,全波仿真确实更为普遍,因为用户无需为它提供波矢或相函数,它能解决的问题类型也比波束包络仿真更全面。另一方面,如果满足波矢已知的前提,波束包络仿真就能够大量减少自由度。正如上一篇博客文章所述,仿真的内存占用很大程度上取决于自由度的数量。但是不要随处滥用波束包络仿真!我们接下来将在另一个案例中故意选择错误的波矢,同时研究所发生的情况。
选择最恰当的波矢
在上文的理想自由空间案例中,我们选择了单向的波矢,在新案例中,我们对硅制板应用相同的设置。有一点需强调,我们很清楚选择的单个波矢的解会是左行和右行波的叠加,它一个极其错误的选择,仅用于演示目的。在这个案例中,我们弃用包含用户定义相函数的双向公式,盲目地采用一个“猜测出”的单个波矢\mathbf{k_G} = n\mathbf{k_0} = \mathbf{k},并研究会带来什么样的不良后果。使用拟设后,可将电介质板的内部描述为
其中左侧为要计算的解,右侧为匹配的项。现在为了研究解的空间变化,我们对方程进行一些处理。
我们特意使\mathbf{k_G} = \mathbf{k},方程由此可简化为
由于\mathbf{E_1}和\mathbf{E_2}是常数,且由电介质板边界上的 Fresnel 关系确定,因此得出的解中唯一的空间变化来自exp\left(-j\left(\mathbf{k+k_G}\right)\cdot\mathbf{r}\right)。同时电介质板对网格的最小要求取决于这个振荡项的“有效”波长
此波长等于原始波长的一半。现在我们将波束包络仿真的网格当作了波长的因变量,而且选择此波矢后,电介质板要求的网格密度变成了全波仿真的两倍。选择单个波矢,并将其应用于具有多次反射的仿真实在是个糟糕的决定。当然,我们确实可以直接将网格密度增加一倍,从而获取正确的解,但这恰恰违背了起初选择使用波束包络仿真的意图。因此,一定要选择最恰当的波矢。
仿真结果
另一个实际的问题是,如何比较全波仿真和波束包络仿真的结果?二者均是对具有相同材料属性和几何结构的模型求解 Maxwell 方程,因此像预期一样,所得的各项结果(透射值、反射值、场值)基本一致。不过两个仿真的结果存在细微的差别。
借助波束包络仿真,可以实现对在电介质板中向右侧传播的波的电场的计算。当然,这是因为我们求解了向右和向左两个方向传播的波,对这两个贡献求和即可得到总物理场。这些结果可以从全波仿真中提取,不过需要额外的自定义后处理,而且也并非适用于所有情况。波束包络仿真的计算时间相对较短,然而却能提供更多的信息,这似乎有违常理。但是请您务必记住,这只是在使用了拟设后的模型求解结果。
高频建模接口的结论和思考
通过使用电磁波,频域接口和电磁波,波束包络接口,我们研究了关于自由空间中的电介质板的简单案例。对比全波仿真和波束包络仿真,后者具有能处理大型仿真的能力,但前提是我们能预先详细了解仿真模型中各处的波矢(或相函数)。全波仿真不需要提前了解波矢,但其模型必须根据波长进行网格剖分,而波束包络仿真则对包络函数的变化剖分网格。另外值得一提的是,大多数波束包络网格往往需要三个以上的单元,这一条件只有在本文的案例中才是可行的,这是因为我们使用的是一个自带解析解的教材式案例,它常被用作教学模型。如您希望了解更具实用性的案例,请参考官网“案例下载”中的Mach-Zehnder 调制器或自聚焦 Gaussian 光束。
请注意,在 RF 模块和“波动光学”模块均可以使用电磁波,频域接口,不过其对应的功能稍有不同。本文讨论的全波仿真在这两个模块中均可执行,但是波束-包络仿真只能使用“波动光学”模块。如您希望了解 RF 模块与“波动光学”模块的全部差别,请参考 COMSOL Multiphysics 产品的技术规格表。
更多资源
- 查看相关博客文章
- 观看以下视频:
- 参加当地的培训活动,提升针对电磁学的建模能力
- >欢迎,咨询您在建模中遇到的问题



评论 (0)