使用 COMSOL® 计算和使用部分电感

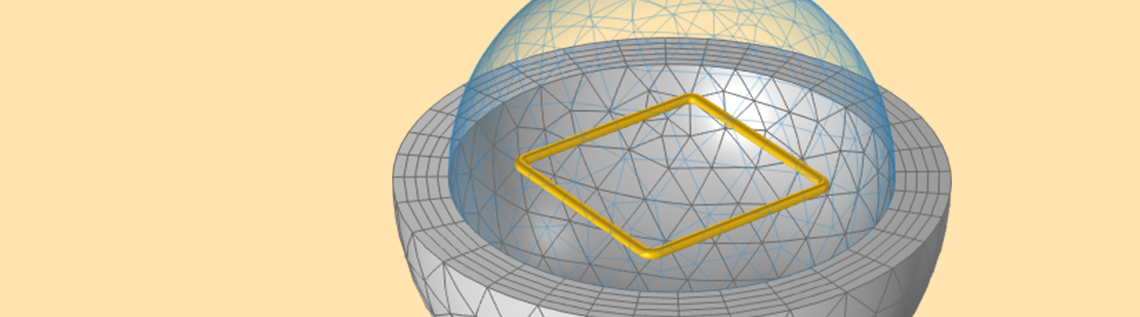
为了求解由非磁性材料组成的电气系统的稳态与频域电感矩阵和交流电阻，COMSOL Multiphysics^®软件 6.0 版本对 AC/DC 模块的磁场，仅电流接口的功能进行了扩展。这对于分析印刷电路板和电源总线系统非常有用，因为可以计算总电感和部分电感。然而，我们需要理解部分电感的概念才能正确解释和使用这个功能。接下来，让我们来了解更多详细内容！

定义和计算总电感和部分电感

为了理解总电感和部分电感，我们假设一个正方形线圈模型，如下图所示。当电流沿着这个闭合回路流动时，周围空间会产生磁场。我们可以通过求解空间中存储的总磁能W_{m}^{tot}和流过线圈的电流I，由公式L^{tot} = 2 W_m^{tot}/I^2定义和计算总电感L^{tot}（通常简称为“电感”）。这个直径 1mm 电线的方形环路，边长为 2cm，总电感为 50.6nH。

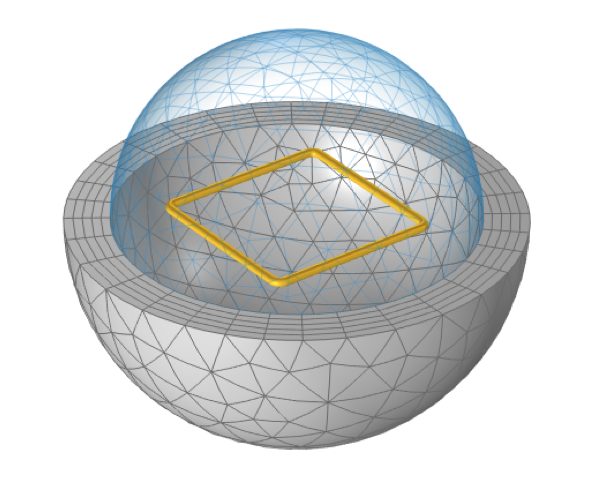
位于球形自由空间域内的通过无限元域截断的正方形空芯线圈，可以由理论公式计算出总电感。

该模型使用了由无限元域截断的球形域，整体建模方法与 COMSOL 案例库中的亥姆霍兹线圈案例非常相似，其中同时使用了磁场，仅电流接口和磁场接口进行计算，并证明了这些公式给出的结果相同。

尽管磁场、仅电流和磁场接口都可以使用，但这两个公式之间存在许多差异。现在，我们只关注使用 注磁场，仅电流接口需要满足的三个要求：

1. 不存在导磁材料，例如电感器磁芯。
2. 所有导体采用实体建模。
3. 不仅可以计算总电感，还可以计算部分电感。

很显然，本示例中的圆线环形线圈模型满足前两个要求，因此我们现在只需要关注第三点：部分电感的计算。

虽然总电感的概念需要一个完整的电流环路才能定义，但部分电感的思想是将整个环路细分为多个部分，每个部分都贡献了各自部分的自感和互感。这些贡献叠加后产生整个环路的总电感。从理论和建模的角度来看，我们完全可以自由选择分割方法，并且可以选择最适合我们工程目的所需的任何细分。

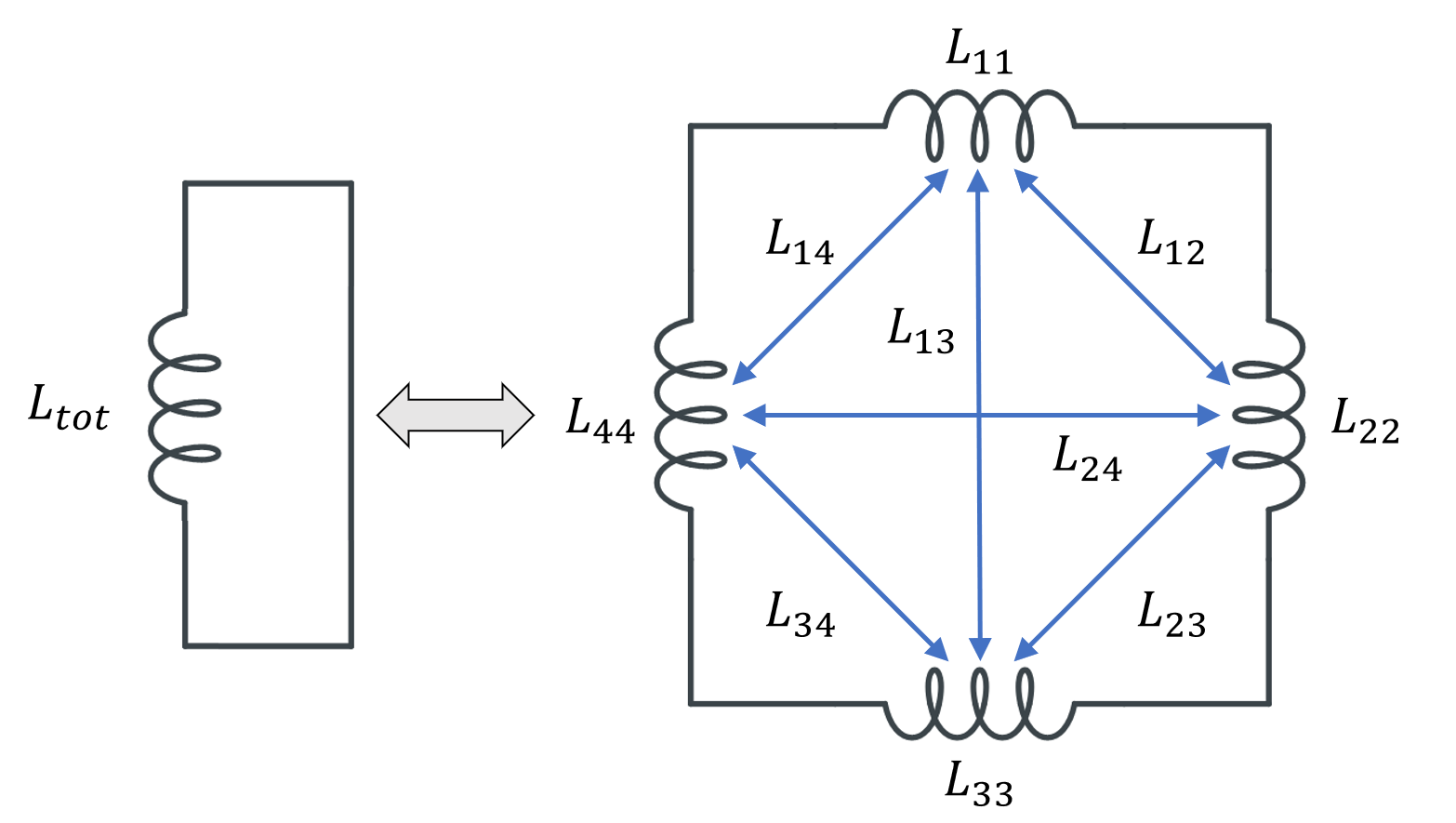
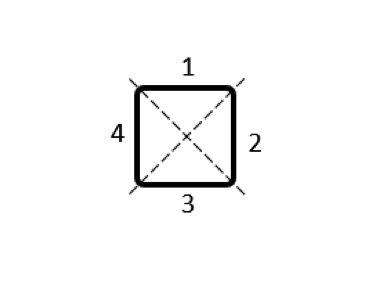
将单个电感细分为 4 个部分，有 4 个部分自感和 12 个部分互感。由于对称，我们仅命名了 12 个互感中的 6。

下面的表格列出了细分导体体积的几种不同可能方案。对这些域中的每一个进行建模时，使用单独的导体特征，在每个域的任一端施加终端和接地边界条件，并使电流总是沿着环路以相同的方向流动。现在我们得到的输出是一个部分电感矩阵，这个矩阵的数值非常值得研究。我们将矩阵对角线上的项称为部分自感，将非对角线项称为部分互感。

线圈细分	部分电感矩阵 (nH)
	\begin{bmatrix}11.84 & 0.85 & -0.89 & 0.85\\0.85 & 11.84 & 0.85 & -0.89\\-0.89 & 0.85 & 11.84 & 0.85\\0.85 & -0.89 & 0.85 & 11.84\\\end{bmatrix}
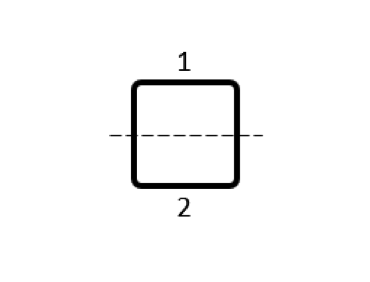
	\begin{bmatrix}14.0 & 0.2 & -1.75 & 0.2\\0.2 & 14.0 & 0.2 & -1.75\\-1.75 & 0.2 & 14.0 & 0.2\\0.2 & -1.75 & 2& 14.0\\\end{bmatrix}
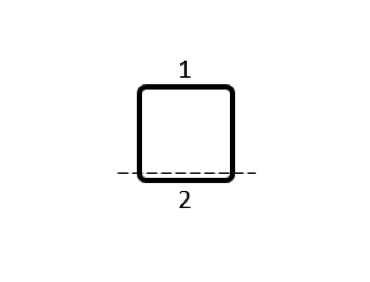
	\begin{bmatrix}25.38 & -0.08 \\-0.08 & 25.38 \\\end{bmatrix}
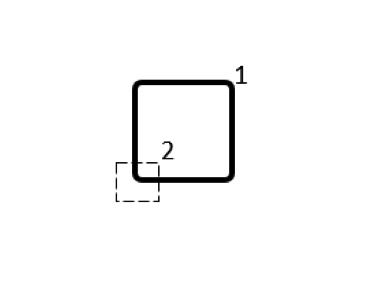
	\begin{bmatrix}38.4 & -1.3 \\-1.3 & 14.8 \\\end{bmatrix}
	\begin{bmatrix}49.3 & 0.5 \\0.5 & 0.3 \\\end{bmatrix}

选择不同线圈细分的部分电感矩阵表。矩阵项的总和始终相同。

请注意，部分自感始终为正，在这种情况下，它比任何部分互感大得多，部分互感可以是正的也可以是负的。矩阵所有项的总和等于总电感：L^{tot}= \sum_{i,j}
L_{ij}。无论线圈如何细分，这都是成立的。然而，对于不同的细分选择，部分电感矩阵可能会变得更加受自感支配。

基于这一观察，即线圈的某些细分会产生对角线占主导地位的部分电感矩阵，对于上表中的第一个细分，我们有理由在自由空间中仅建立一个线圈部分的子模型，如下图所示，其中使用单个导体域，两端都施加了终端和接地条件，从而仅输出一个11.84nH 的部分自感。这与之前计算的部分电感矩阵的对角项相等。

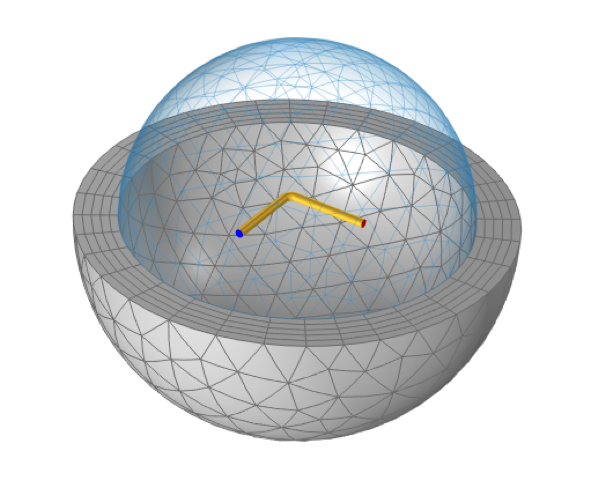
四分之一方环线圈的模型可以计算部分自感，并可以很好地预测总电感。磁场，仅电流接口允许线圈终止于自由空间，末端具有终端和接地条件。

现在，上述模型似乎在导线末端（应用终端和接地边界条件）产生和终止了电流，但这就是磁场，仅电流接口与众不同的能力：它能够计算任何一组导电域的部分自感（和部分互感），即使是那些未连接在闭环中的域。

下一个示例，我们将考虑线圈的第二个细分。对于这个细分，我们仅以一段短而直的圆导线示例。这是一个特别有趣的案例，因为已经有很多手册给出了解，如下表所示。在这种情况下，我们将在一个频率范围内观察电感和交流电阻，也就是从趋肤深度远大于导线直径的低频过渡到趋肤深度远小于导线直径的高频。为了求解这个问题，我们必须使用边界层网格来计算集肤效应。另外，我们没有使用无限元域，而是在球面建模空间的边界上使用默认的外部边界条件，这是基于模型内的电流应用近似的边界条件，因此需要研究计算域的半径。

圆导线交流电感和电阻的手册值
低频电感	\frac{\mu_0}{2\pi}\ell\left[ \ln\left( \frac{2\ell}{r}\right) -\frac{3}{4}\right]
高频电感	\frac{\mu_0} {2\pi} \ell\left[ \ln\left( \frac{2\ell} {r}\right) -1\right]
直流电阻	\frac{\ell}{\sigma \pi r^2}
交流电阻	\frac{\ell} {\sigma \pi (2r\delta – \delta^2)}
长度：\ell，半径：r, 电导率：\sigma,集肤深度：\delta =\sqrt{ \frac{2}{\omega \mu_0\sigma}}

仿真结果显示了直流电阻与手册完全一致，低频电感也相当接近（小于1% ）。后者的轻微误差与末端效应有关，分析的导线长度越长，直导线的模拟值和手册值之间就越接近。

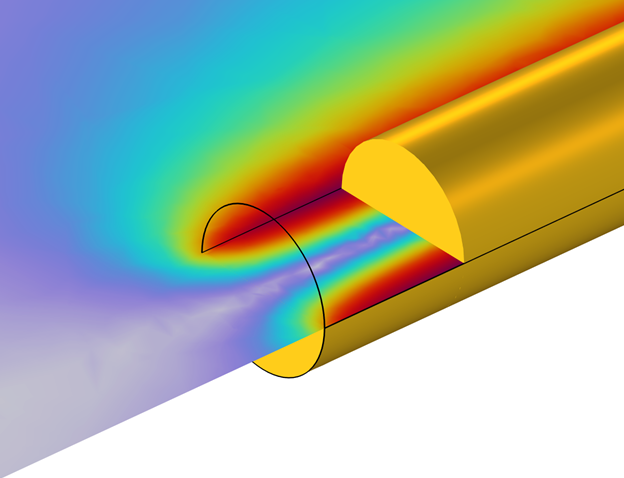
电线内部的剖面图特写。计算的磁场显示了末端效应。

交流电阻在很宽的范围内也表现良好，但在较高频率下存在明显偏差，因为此时趋肤深度远小于导线直径，这种偏差是集肤效应引起的，在如此高的频率下，需要非常精细的边界层网格来解决这个问题。

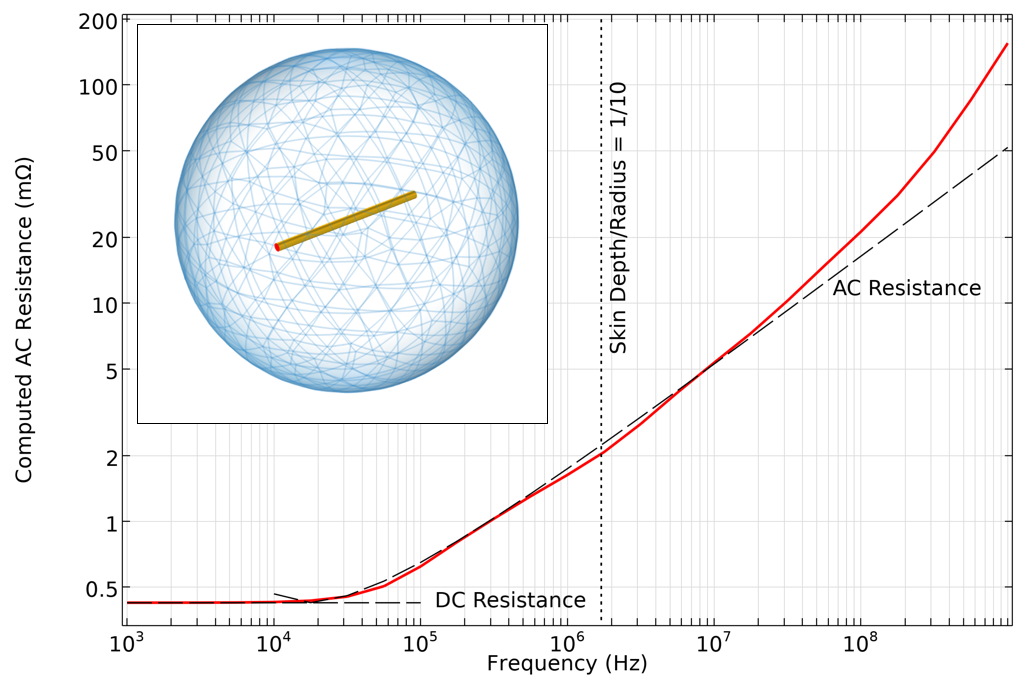
直导线交流电阻的计算结果与基于趋肤深度的手册方程对比。在非常高的频率下，需要非常精细的网格，并且位移电流可以忽略不计的假设不再成立。

在这些较高的频率下，还有另一个问题：可以忽略附近电介质的假设不再成立。换言之，位移电流开始变得显著。在这种情况下，我们应该改用磁场公式，它可以将电流建模为在导体表面上流动，而不是求解体内的场。磁场接口求解位移电流，以及导电和感应电流。磁场，仅电流接口忽略了所有位移电流，仅考虑导体域本身内的传导电流和感应电流。

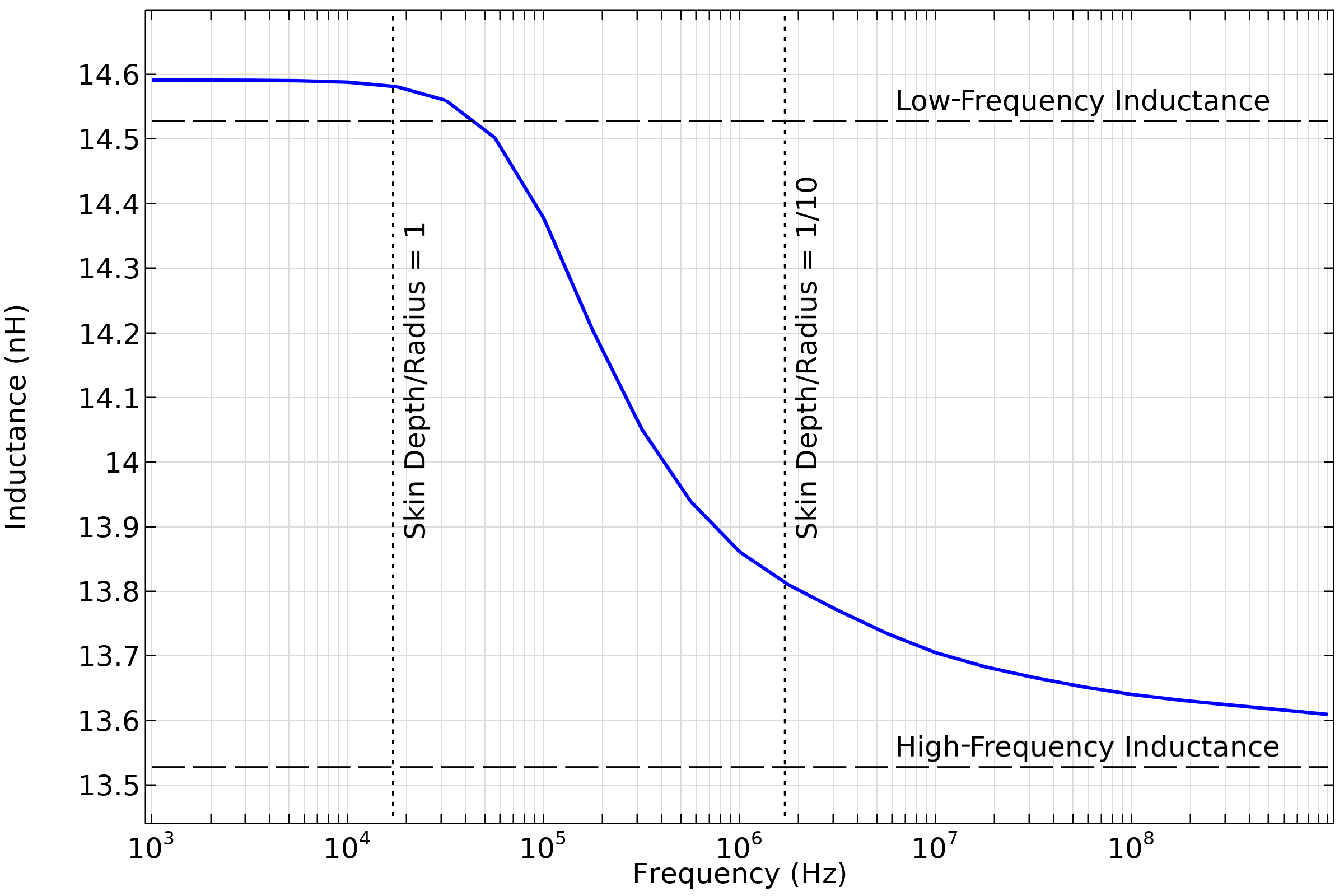
与忽略末端效应的低频和高频手册解相比，计算出的直导线的部分自感。

综上，我们已经了解了如何计算部分电感，以及这个公式的适用范围，那么如何才能自信地使用这个接口呢？重要的是要注意，我们永远无法测量这些部分电感，因为只有闭环的总电感是可测量的。但是，假设我们有一个非常复杂的大型系统，那么很可能计算总电感的成本非常高。

在我们只对重新设计的一个小型子系统进行模拟前，需要做出两个假设：

1. 建模和非建模组件之间的部分互感对总电感的影响相对较小。
2. 未被建模的组件的部分自感保持相对固定。

如果这些假设成立，那么只对系统的一个部分（或几个部分）进行建模是合理的。尽管我们可能永远不想计算总电感，但只要理解了上述假设（以及这些部分电感对总电感的贡献的概念），该子模型仍然具有预测价值。

现在，我们来看几个典型的例子来说明这个接口的适用性。

磁场，仅电流接口的典型应用

磁场，仅电流接口适用的情况包括：

• 计算电路板元件的部分电感
• 电源总线系统
• 电缆和连接器
• 绝缘栅双极晶体管 (IGBT)
• 附近没有磁性材料的线圈

下图所示的一个具有多个空芯电感器的电路板案例就是一个应用示例。凭借上述介绍的知识，我们现在可以自信地建立模型来提取单个电感器的部分自感，或几个紧密间隔的电感器之间的部分自感和部分互感。有关相关示例，请查阅PCB 线圈的电感矩阵计算案例。

一种包含许多空心电感的电气元件。通过使用磁场，仅电流接口，可以一次计算其中几个电感的交流电阻和部分电感矩阵。

结束语

在这篇博文中，我们介绍了如何使用磁场，仅电流接口来计算总电感和部分电感，以及交流电阻。首先，我们通过一个可以与其他方法进行对照验证的案例，验证了总电感计算的整体正确性。然后，我们研究了部分电感以及部分电感和总电感之间的关系。我们还研究了交流电阻的计算，这有助于我们了解如何有效使用磁场、仅电流接口进行频域建模的机制。有了这些信息，我们现在可以自信地解决这一类型的问题了！

点击此处，了解AC/DC 模块或联系我们了解更多详情。