在模拟多孔介质中的流动时,使用均质化的宏观方法可以有效地简化真实多孔材料的几何复杂性。但是如果我们不知道有效的宏观特性是什么,该怎么做?这篇博客,我们将研究如何从完全解析的微观子模型中提取孔隙率和渗透率的宏观流动特性。
使用宏观方法模拟多孔介质流
在上一篇博客中,我们讨论了可用于模拟多孔介质中宏观流动的接口,包括达西定律接口。求解达西定律可以深入了解许多不同的物理系统,在这些系统中,模拟完全解析的微尺度系统实际上是不可能的。在石油和天然气、土木工程以及生物和医学工程等应用领域中,微观和宏观系统的长度尺度之间存在巨大的差异,因此带来了求解的困难。

一个多孔材料的例子:海绵。
宏观方法假设孔隙空间的行为由两个平均量来量化:
- 渗透率
- 孔隙率
渗透率是指描述流体流过孔隙的阻力。孔隙度的定义为孔隙空间的体积分数,决定了表观平均流速。至于表观流速,是指通过均质域的等效速度,也可以理解为:通过孔隙空间的微观流动在宏观尺度上是均匀分布的。
如果孔隙率和渗透率未知,就必须通过实验结果来量化这些材料特性。通过模拟进行的数值实验也可以用来分析完全解析的包括空隙和固体颗粒得几何结构。通过在微尺度几何上求解纳维-斯托克斯方程(或其对低雷诺数的线性近似,称为斯托克斯流或蠕动流),可以提取多孔介质的孔隙率和渗透率。
创建微型多孔几何结构
在研究多孔介质的孔隙率和渗透率之前,我们必须讨论微观几何结构的创建。这不一定是一个简单的过程!创建这类几何结构通常需要专门的第三方软件(如 Simpleware 或 Mimics®)重建扫描图像数据,尤其是复杂的 3D 几何图形。这里,我们将重点研究 2D 横截面几何结构,例如由扫描电子显微镜(SEM) 图像生成的横截面。
接下来,我们将要介绍的孔隙尺度流动教程模型,是将一个图像文件作为函数直接导入 COMSOLMultiphysics®软件中创建的。下列博客中介绍了由这个函数重新构建几何结构得类似方法。
对于过于复杂或包含影响网格分辨率的小几特征的几何图形,我们可以使用孔隙尺度流动教程中采用的方法,这将在下一篇博客文章中讨论。
使用 COMSOL Multiphysics®中的蠕动流接口
孔隙尺度流动模型求解了完全解析的孔隙空间几何。我们可以使用 COMSOL Multiphysics 中的后处理工具来提取孔隙率并使用达西定律计算渗透率。下面,我们来快速浏览一下这个案例。
由整个几何形状的尺寸 640×320μm (孔隙空间中的通道宽度更窄),我们知道特征长度尺度L很小。此外,考虑到流动是由 2 Pa 压力梯度驱动的缓慢流动,典型的速度值U应该很低。因此,给定类水流体的密度 ρ=1000kg/m3,动力黏度 μ=0.001Pa*s,我们可以安全忽略 Navier-Stokes 方程的惯性项并使用蠕动流接口求解,因为雷诺数 Re 明显小于 1。
如果想获取更多信息,请阅读博客:如何表征流动并选择正确的接口。
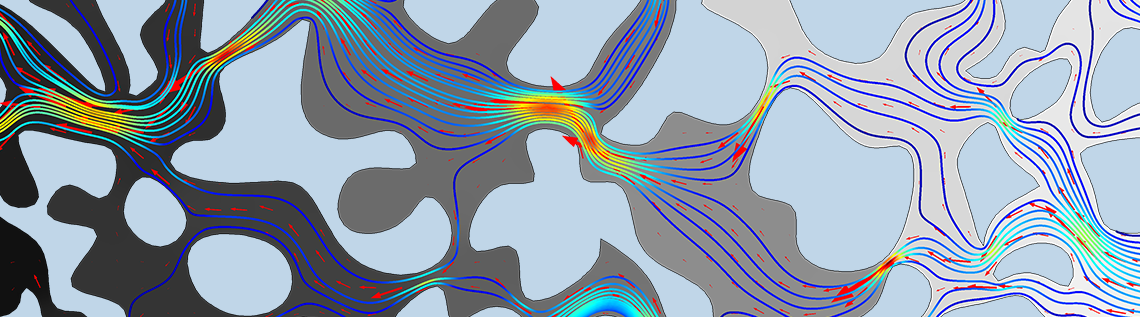
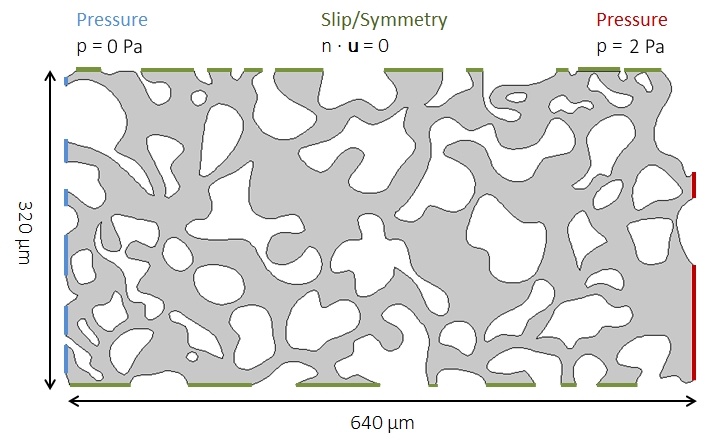
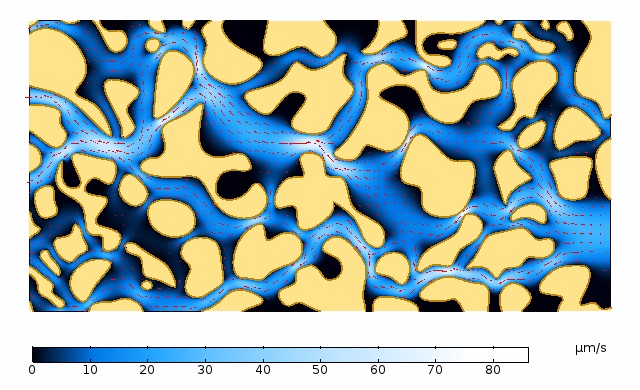
使用入口和出口条件从右到左施加压降。由于该模型是我们希望描述的多孔介质的代表性横截面,因此沿边界规定了一个对称条件,该条件是由顶部和底部的几何形状截断引起的。下面的左侧图显示了这些边界,右侧的图像显示了结果,用含速度大小的颜色图和流动方向的箭头矢量来显示。
左图:使用蠕动流接口求解的完全解析微尺度模型的几何形状和边界条件。右图:速度大小颜色图,红色箭头图表示通过孔隙空间的流动方向。
计算多孔介质的孔隙率和渗透率
计算孔隙率
首先计算孔隙率por。在这个 2D 示例中,我们需要计算总面积和由计算域表示的面积。
我们可以简单地把总面积作为一个变量:A_tot = L*H来计算。为了确定孔隙空间的面积A_por,我们可以在流域上对表达式 “(1)” 进行积分。这可以通过使用积分组件耦合的方法轻松实现,这是一个自定义的运算符,可以在域、边界等处积分任何表达式。下面的图片中显示了用于计算A_tot、A_por和por的设置。
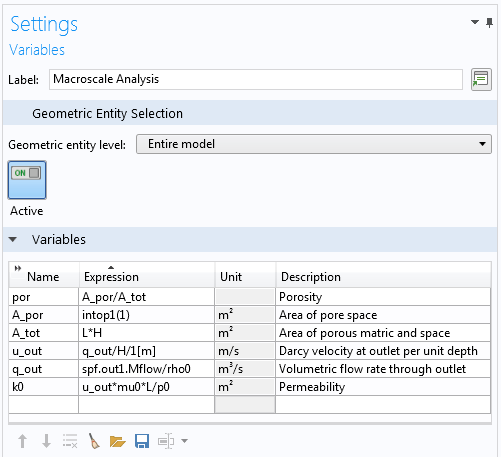
用于计算孔隙率和渗透率的变量定义。
计算渗透率
上图还显示了渗透率k0是如何计算的。达西定律指出:
{u}
= -\frac
{\kappa} {\mu}
\nabla p
其中,u是达西或表观流速,κ是渗透率,μ是动力黏度,∇p是压力梯度。
我们可以在蠕变流接口中借助预定义变量计算达西速度。
变量spf.out1.Mflow定义了通过出口边界的质量流量,我们可以除以恒定密度 ρ0,来获得体积流量。然后除以多孔介质的高度,再除以 1 m,来考虑 2D 近似并获得x方向的达西速度。
通过重新排列公式(1)并替换\nabla p = \frac{\Delta p} {L},我们可以使用已知的压降p0,穿过多孔区域的长度L来评估变量k0的渗透率。
结果表明,这种微观尺度代表了具有 0.553 的孔隙率和 4.59×10-12m2的渗透率的多孔介质。
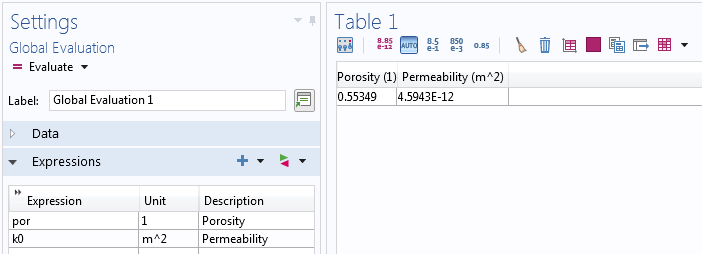
由完全解析的流动子模型计算的孔隙率和渗透率的结果表。
总结性思考
在这篇博客中,我们讨论了如何使用仿真来推导出通过多孔介质的流动的宏观特性——在完全解析的微观尺度子模型中求解自由流动。有了这些信息,我们就可以将这些参数作为更具描述性的宏观模型的输入。更重要的是,这是了解在一个用户界面友好的仿真App中使用什么输入的理想方式,例如这个考虑射孔井生产率和安全性的仿真 App 示例。
其他资源
- 阅读这篇博客,了解如何模拟多相催化
- 查看有关模拟多孔材料的有效扩散系数的教程



评论 (0)