课程：在 COMSOL® 中模拟电磁线圈

您是不是正在寻找一些有关电磁线圈建模的资源，可以帮助您快速学习使用 COMSOL Multiphysics^®软件和 AC/DC 模块？今天这篇博文，我们整理了一门视频课程的主要内容，来帮助您了解如何对电磁线圈进行建模，旨在帮您掌握构建这类模型的关键要点。接下来，我们快速浏览一下这些视频中的内容，以及了解如何充分利用这些课程！

电磁线圈建模入门

最简单的电磁线圈是单匝载流导线，在几乎任何关于电磁线圈建模的主题中我们都能看到对它的介绍。假设单匝线圈可以看作是一个闭环，那么它就是轴对称的，或围绕中心线不变，这通常是一种合理的工程简化。

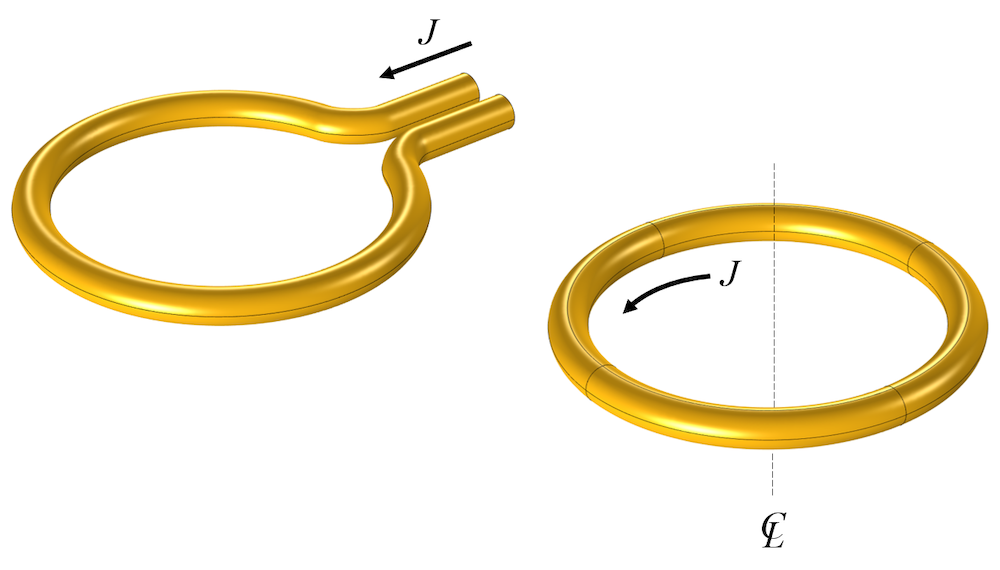
也可以使用 2D 轴对称假设对单匝线圈进行建模。

我们的线圈建模课程正是基于这个假设开始的。在课程的前 5 部分，我们将在 2D 轴对称空间中建模。

第 1-5 部分

在课程的前 5 部分，我们提供了有关线圈建模的基础知识，以及在其他部分课程中需要的信息。首先在直流条件下，我们从头开始完整建立了一个单匝线圈模型。空气域以一个无限元区域为边界。假设 1 安培的电流通过线圈，在二维轴对称平面中对其进行建模。我们还提供了一些有关为什么以及如何使用二维轴对称假设的额外背景信息。

在运行模型之后，我们还对线圈的电导率和线圈电阻进行了评估，然后将线圈移入频域。对用 1 安培电流励磁的线圈进行建模，并假设励磁电流变化是正弦，频率已知。

在直流和交流情况下，建立并检查线圈模型后，我们讨论了建立这类模型时应该注意的潜在问题。

在这之后，我们继续通过模拟线圈与电路的连接来扩展这个线圈模型。通过引入一个磁芯和一个次级拾取线圈来实现这一点，流过初级第一线圈的一些电流通过该线圈被拾取。然后，我们展示了如何通过一些后处理将线圈之间的电流大小和方向可视化。

从这里开始，我们开始对包含多匝和不同绕组模式的线圈进行建模。此外，我们还将对第一共振频率以内和附近的线圈以及扁平线圈进行建模。最后，全面介绍了磁场物理场接口以及其中包含的不同功能，您可以在构建线圈模型时使用这些功能。

完成这部分视频课程中的学习后，您将对二维轴对称线圈建模技术的基础有所了解。

线圈中的电磁加热

COMSOL Multiphysics 中的 AC/DC 模块和传热模块最常见的用途是模拟感应加热，即线圈随着时间的推移对工件加热的过程。在课程接下来的 5 个部分，我们将深入讨论这个主题。

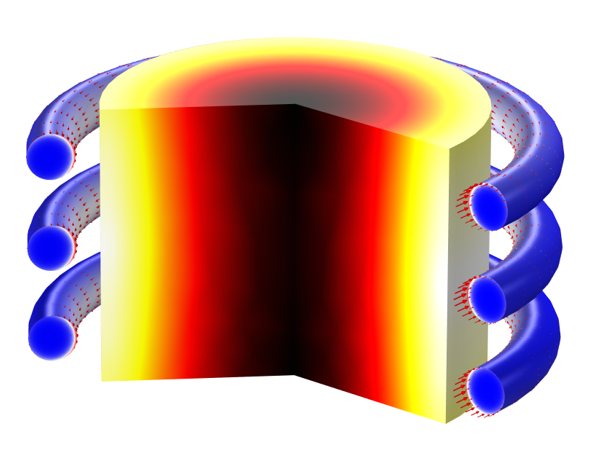
具有非线性材料特性的工件随着时间的推移被感应加热。

第 6-10 部分

在课程的第 6 至第 10 部分，我们演示了设置和解决感应加热线圈建模问题的完整建模过程。首先在自由空间中建立了一个三匝线圈的 2D 轴对称模型，并指定流过每匝线圈的电流为 1 千安培,在中心放置了一个由钛合金制成的工件。我们需要在频域中以 10kHz 的恒定频率建模。在计算模型后，进行了一些后处理以查看工件部分的损耗。

正是从这里开始，我们将最初的电磁学问题扩展为电磁加热问题。为了找出电磁损耗如何导致温度升高以及上升到什么程度，向线圈模型添加了第二个物理场，即传热。之后，我们将从使用标量、常数值到模型输入的函数（在本例中是温度）几个方面，来向您展示如何修改材料属性。然后，继续扩展模型，演示了工件的加热曲线如何随时间变化，以及在多个频率下求解。

从这里开始，我们开始深入探讨关于求解器的各种主题。通过在热力模型中包含对流和辐射来解决以前没有涉及的热建模影响，以及如何模拟运动部件的加热。

完成本课程的这一部分学习后，您应该有信心解决大多数线圈加热问题。

力、运动、非线性等问题的建模

本课程接下来的五个部分涉及另一种多物理场：电磁力与零件的变形和运动之间的耦合，例如在螺线管中的该类问题。

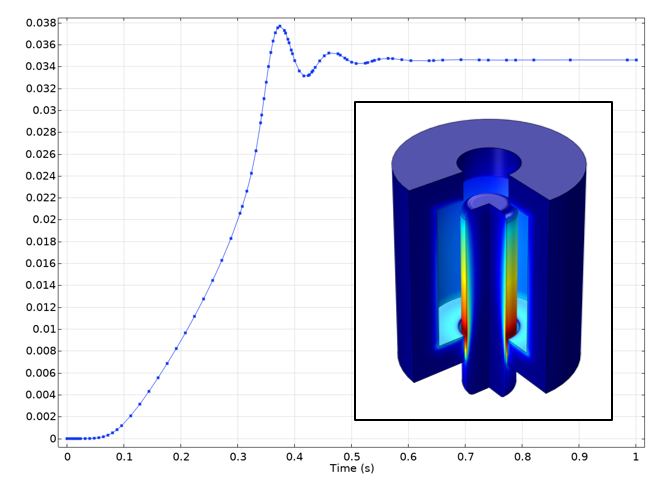
不同时间下螺线管执行器中的位移。

第 11–15 部分

在课程的第 11 至第 15 部分，我们建立并使用了几种不同的线圈模型几何结构来进行各种分析。之前我们通常使用单一几何结构和模型设置，通过对它们进行更改使模型逐渐复杂并进行扩展分析。

首先，我们演示了如何建立电磁力模型并做到准确无误，这是通过以下方式来实现的：向模型添加力计算特征，使用全局计算特征找到在模型线圈中观察到的总力。然后，我们探索了如何确定所评估的力的准确性，这可以通过执行网格自适应快速、轻松地完成。随后生成的仿真图显示了力的大小与网格细化的函数关系，以此观察力是否开始收敛到某个定值。

接着，我们继续讨论如何建立一个在线圈中移动并产生电流的磁铁模型。其中，磁铁是使用安培定理域特征来定义的，而运动是使用软件中的几个移动网格特征定义的。在求解该模型时，由于模型的源项和初始值不一致，我们遇到了一些与求解器设置相关的问题，我们将详细说明如何解决这些问题。

从这里开始，我们开始对上一个问题进行逆向建模，即模拟一个螺线管执行器。这一次，我们有一个线圈，然后向其施加随时间变化的电流，以引起附近零件的运动。之后，我们将演示如何对具有非线性磁芯材料的电感器进行建模。在这个过程中，我们会触及之前模型中讨论过的主题，例如解的准确性和收敛性。我们还向您演示了如何通过整合线圈电流方程、通过全局评估接口将另一个方程引入模型，以及使用 at 运算符执行全局评估，从而使核心区域的周期平均损耗可视化。

电磁建模系列主题将以另一个模型结束，在该模型中我们采用一个线圈并优化该线圈，使 B 场在几何体的中心线尽可能均匀分布。我们定义了一个目标函数，并通过改变流经线圈的电流和线圈位置来改进该函数。

完成这部分课程学习后，您应该对大多数线圈模型的建模、计算和评估力、运动和非线性问题比较熟悉了。

模拟 3D 线圈

线圈建模课程的最后五个部分解决了与 3D 线圈建模相关的问题。尽管线圈建模的大多数概念通过 2D 轴对称模型就可以学习，但仍有一些独特的问题需要在 3D 中阐述。

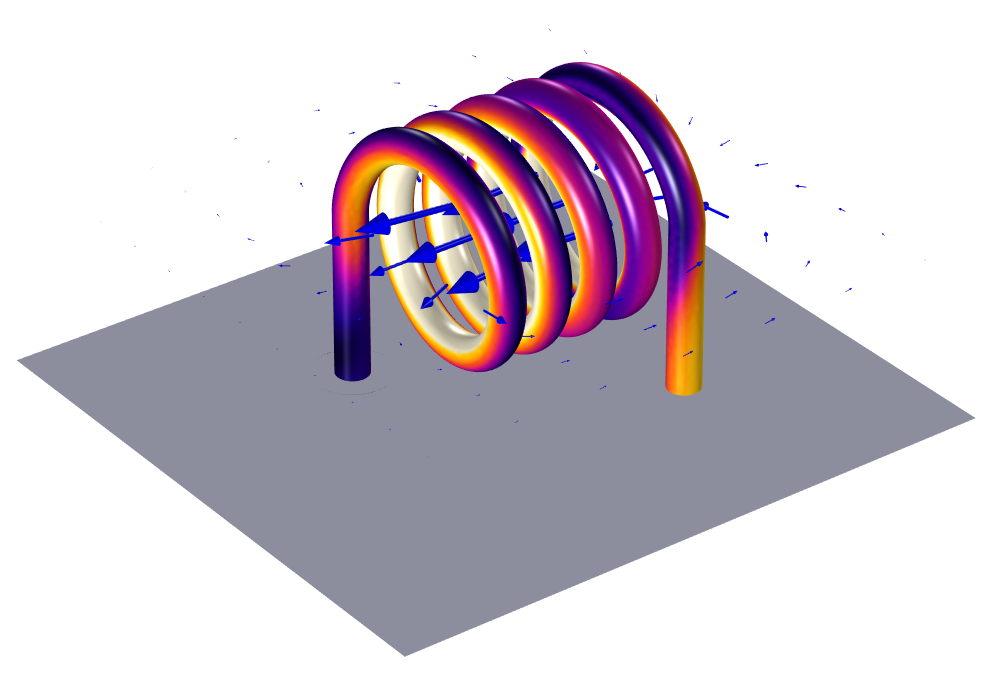
显示线圈电流大小和周围磁场的 3D 线圈模型。

第 16–20 部分

在课程的第 16 至第 20 部分，我们建立了第一个 3D 线圈模型，并在静止的 DC 状态下求解该模型。在 3D 中构建线圈的几何形状时，我们使用了螺旋图案，并在线圈弯曲的末端将线圈挤出成垂直的直管。在这个过程中，我们向您演示了一些不同的方法，您可以使用这些方法来确保线圈几何形状是单一域，也就是使用删除实体、并集或形成复合域操作来完成，但是这并不是必需的。与之前的 2D 轴对称线圈模型不同，向 3D 模型中添加线圈域特征，包括几何分析子特征，我们需要在其中指定我们希望电流流入和流出线圈的位置。

在计算模型时，我们会收到一条错误消息，然后解释发生这种情况的原因和方式以及如何解决。我们的研究包括一个新的研究步骤——线圈几何分析，首先计算通过结构的电流方向。然后，使用磁场接口成功求解模型后，使用磁场和电场接口求解相同的问题。

在完成这些单匝线圈模型后，我们将演示对不同类型的线圈进行建模的专门功能。我们讨论并演示了如何通过使用近似等效的几何形状和调整线圈域特征设置来模拟多匝线圈的匝数，而不是对多匝线圈的匝数进行显式建模。其他类型的线圈包括薄的带状线圈，紧密包装的线圈，匝间没有间隙的线圈，以及边缘线圈几何形状。软件中的零件库包含多种不同类型的内置线圈可供我们添加和使用。

我们还在线圈模型的空气域中引入了一个无限元区域，并详细讨论了此功能的使用及其物理表示。从这里开始，我们离开静态的 DC 状态，将3D 线圈建模移至频域。我们还讨论了低频、中频和高频区域的线圈建模。此后，我们将讨论如何处理在对这些模型进行网格划分和收敛时可能遇到的一些问题。最后，我们演示了如何模拟共振以及处理线圈之间的耦合。

完成本课程的最后一部分后，您将具备解决 3D 线圈模型的建模基础。我们希望这些资料能够对您使用COMSOL Multiphysics和AC/DC 模块构建线圈模型有所帮助和启发，并能在建模过程中更快、更自信地完成这些工作！