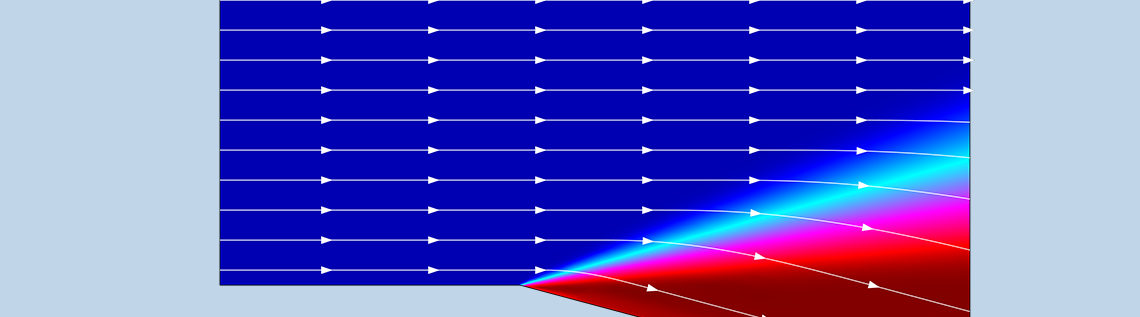
当超音速流绕过一个凸角时,就会出现膨胀波。在分析这种现象时,需要确保模拟结果是准确的,并与现有理论具有很好地一致性。这可以通过 COMSOL Multiphysics®软件和 CFD 模块实现。在这篇博文中,我们将讨论一个超音速膨胀波的基准模型,并将它与无黏性可压缩流动理论进行比较。此外,我们还将分享一些改进这个模型的小技巧。
通过可靠的超音速流动分析改善超音速飞行
比音速(马赫为1)还快的超音速流动不是我们每天都会遇到的,但是它们与航空航天等领域关联密切。例如NASA,它们就研究超音速飞行以推进航空研究,以及设计在超音速下运行良好的飞行器。(他们最近研究的新型超音速客机就是一个例子。)

超音速喷气式飞机。图片由 EyeMindSoul 提供。通过Flickr Creative Commons获得许可(CC BY 2.0)。
仿真是分析超音速流动的强大工具,用来实现各种目标。但是,当我们获得仿真结果时,希望对它的准确性充满信心。COMSOL Multiphysics 包含的一些特点和功能使我们能够生成可靠的结果,用于可信的分析。为了证明这一点,我们将分享一个膨胀波的基准模型,它是超音速流动的重要组成。
膨胀波:超音速流动中的一个重要现象
当超音速流动遇到一个凸角(也叫膨胀角),并远离自身时会发生膨胀波,从而增加面积。(与此相反的情况是,超音速流动转向自身并导致面积减小,从而产生斜激波。)
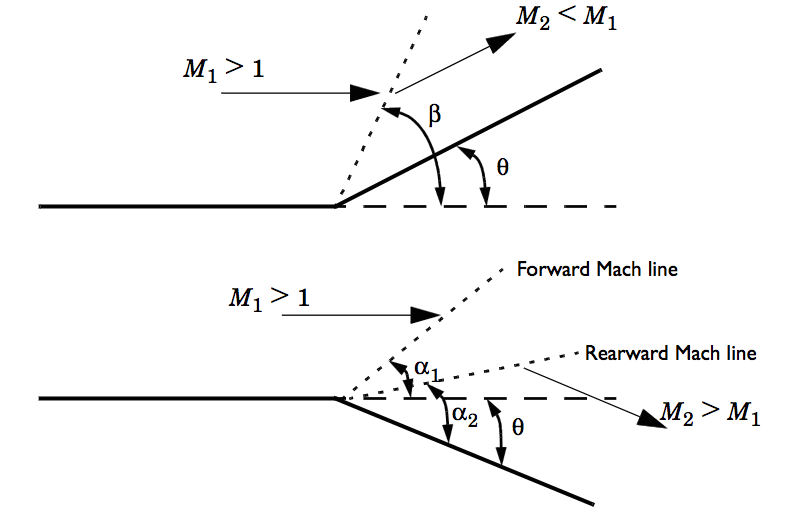
斜激波(上)和普朗特–迈耶膨胀波(下)。
对于超音速膨胀波,也称为普朗特-迈耶膨胀波,激波前后的总条件没有变化,熵守恒。此外,静温、压力和密度会降低,马赫数会增加。膨胀波是等熵过程,它会在流动中产生连续和平滑的变化,从而使流动的总属性保持不变。在这里,总值是流动特性在停滞时产生的值,而静态值表示在一定速度下流动属性的实际值。
膨胀波教程模型有多准确?
COMSOL 案例库中有一个二维教程模型研究了一个膨胀波,它有一个 15° 的膨胀角,马赫数为 2.5 的超音速入口流,并假定出口处有超音速流。在我们的分析中,假设流动是无黏性的,因此对壁面应用滑移边界条件。这个模型中的流体是空气。
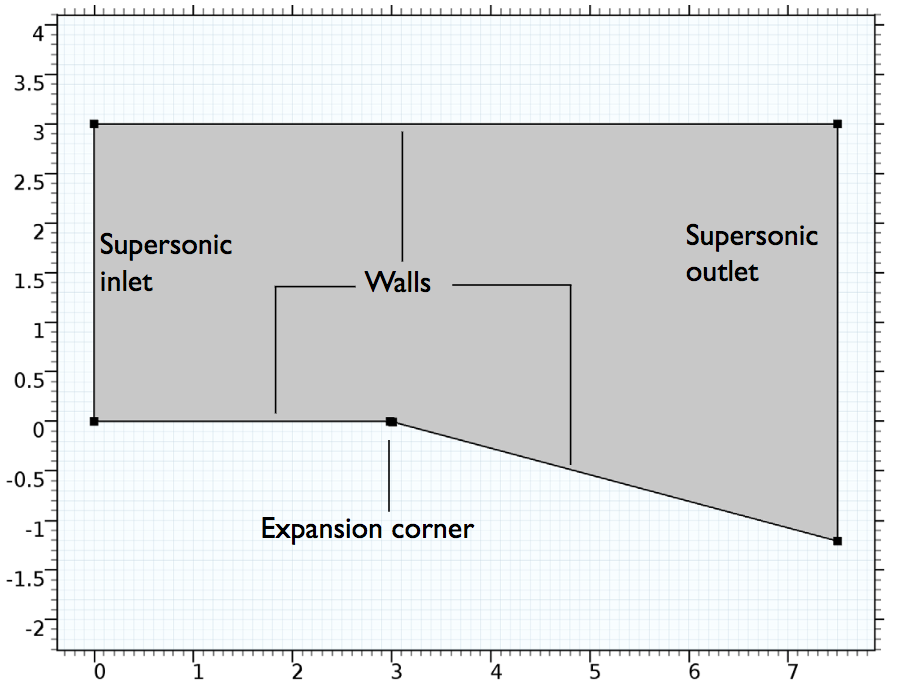
膨胀波的几何形状。
为了解决这个问题,我们使用了 COMSOL 软件的 CFD 模块中的无黏性可压缩流动方程以及高马赫数流动、层流接口。为了证明教程模型的结果是准确的,我们可以将它们与无黏性可压缩流动理论进行比较。现在我们直接来看这些结果。
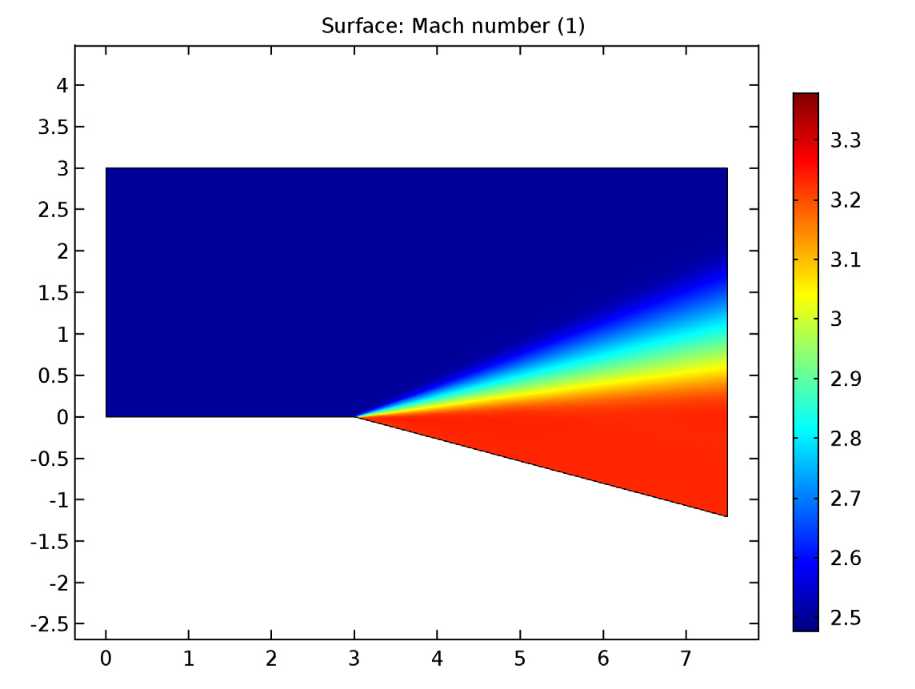
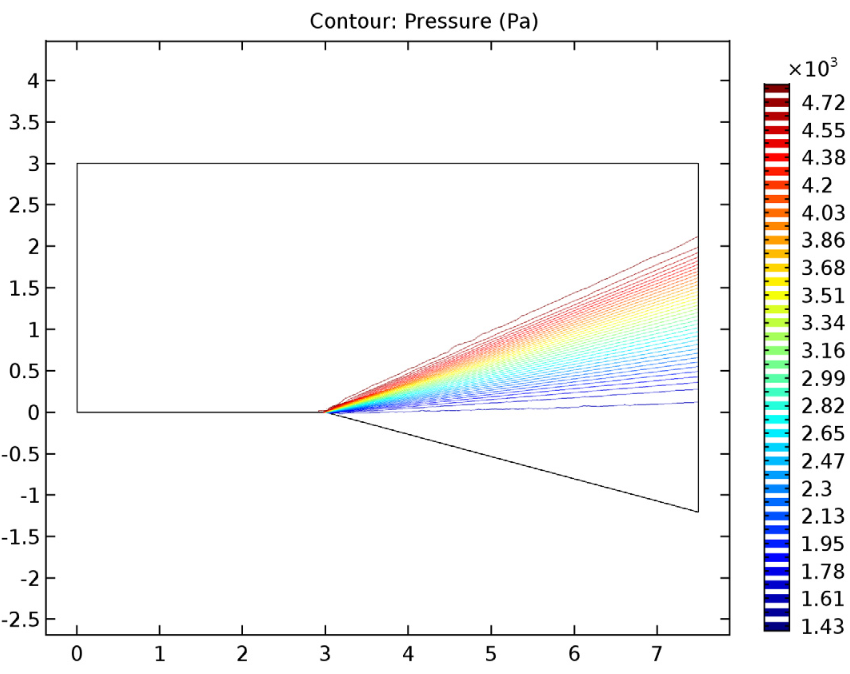
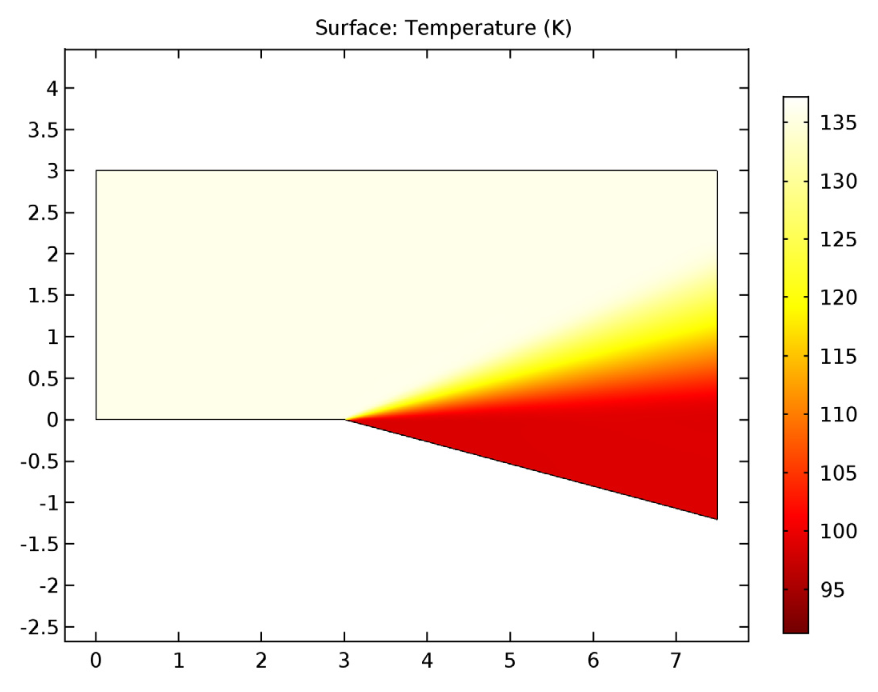
膨胀波的马赫数(左)、压力等值线(中)和温度等值线(右)。
我们看到,经过膨胀角的超音速流动以连续的马赫或无穷小的波膨胀。这使得马赫数增加,同时静压和温度降低,与膨胀波所预期的一致。至于速度流线,它们在膨胀波上平滑地改变方向,最终平行于下面的表面。
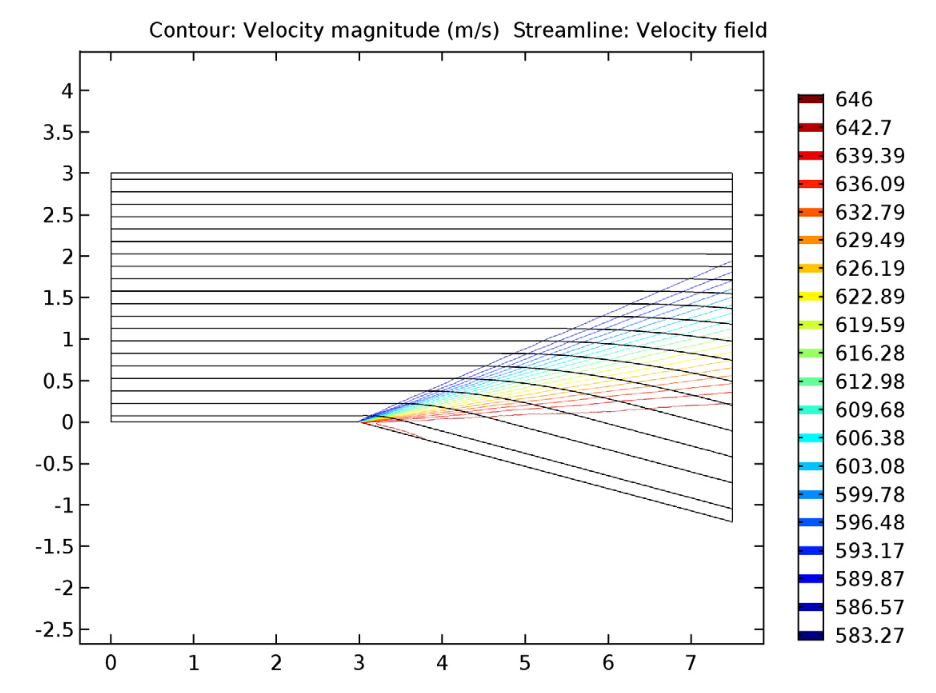
膨胀波的速度分布和流线。
接下来,让我们看看模型的结果与可压缩流动理论的结果相比如何。在下表中,我们看到模拟的马赫数与无黏性流动理论非常一致。我们还可以确认,流动的总属性是守恒的,并且与已有理论相似。
| 马赫数 | 总温度 | 总压力 | 总密度 | |
|---|---|---|---|---|
| 模型值 | 3.2331 | 305.432 K | 82,213 Pa | 0.93787 kg/m3 |
| 可压缩流动理论值 | 3.2372 | 305.432 K | 82,737 Pa | 0.94347 kg/m3 |
由此,我们可以得出结论,我们的模拟结果与从无黏性可压缩流动理论中得到的结果具有很好的相关性。因此,像膨胀波教程模型这样的 CFD 模型可以帮助准确分析超音速流动现象。
单击下面的按钮尝试对文中演示的基准示例进行建模,我们使用了一些简单的技巧对它进行了改进:
- 为避免陡峭的梯度和不连续性,我们将模型中的角变为圆角
- 为了在膨胀波处细化网格,我们使用了自适应网格细化特征
浏览下列教程和博客文章,扩展 CFD 知识
- 查找其他 CFD 基准教程:
- 浏览CFD 博客文章汇总



评论 (0)