虽然利用数学研究化学反应已经进行了一个多世纪,但直到最近,速率方程的数值积分计算方法才被广泛使用。 “需要是一切发明之母”这句古老的谚语在这种情况下是正确的。这篇博客,我们将介绍一个非微观反应系统的经典分析,并看看将简化的解与“真实”的解进行比较会如何。
懒惰的分子
在上一篇博客中,我们介绍了活化能的概念,即分子发生反应所需的能量必须通过“撞击”产生。对于许多重要的反应来说,这个能量相当高。事实证明,有些分子很懒惰,并且很满足于保持其现在的形态。这不一定是一件坏事,比如对牛来说。
牛和包括人类在内的任何有机物一样,本质上都是热力学不稳定的;除了水分,它们主要由碳氢化合物组成,通常是氧化物和氮化物,这是一种潜在的可燃混合物,并且作为二氧化碳、氮和水存在时明显更稳定。热力学表明,这是一个能量上更有利的形式。它们的分解反应的动力学都相当缓慢,因为这些分子缺乏分解所需的活化能。
现在,我们来看一个示例。假设把一块牛排放在一个热的烤架上。如果你这样做了,会看到当活化能大量存在时会发生以下现象:首先,肉会被烤焦,最后,会留下一堆灰(肉的矿物质、无机成分)。这就引出了我的下一个观点:我们人类如何从吃一块(适当煮熟的)肉中获得能量?答案是通过催化作用。
催化剂和酶
催化剂是一种物质,它以某种方式拉动和扭曲一个分子,使其能够按照一种不同的、能量较低的途径进行反应。其结果是,反应可以在更低的温度下突然以非常快的速度进行。催化作用无处不在,大约 95% 的工业化学产品在其生命周期中至少要经历一个催化步骤。
酶是一种重要的催化剂,经过数百万年的优化,可以在非常适宜的温度下工作。酶是使生物系统能够进行维持生命所需的化学反应的大分子(通常由几千个原子组成)。比如当一片面包被嚼一会儿后,就会变甜。这是由于淀粉酶的作用,它是一种存在于人类唾液中的酶,可以将淀粉转化为糖,以便于消化。
胃蛋白酶
回到我们的牛排例子。事实证明,如果没有酶,肉本身会很硬,不好吃而且难以消化。在牛肉进入我们的盘子之前,屠夫就已经把肉挂了几个星期,让一些自然产生的酶开始降解蛋白质,从而使肉变嫩,增强它的整体风味。再往下看,在我们的消化道中负责降解蛋白质的酶被称为胃蛋白酶。胃蛋白酶实际上是第一个被发现的酶,所以我觉得它是本文的一个合适的例子。接下来,我们来仔细研究一下胃蛋白酶的工作原理。
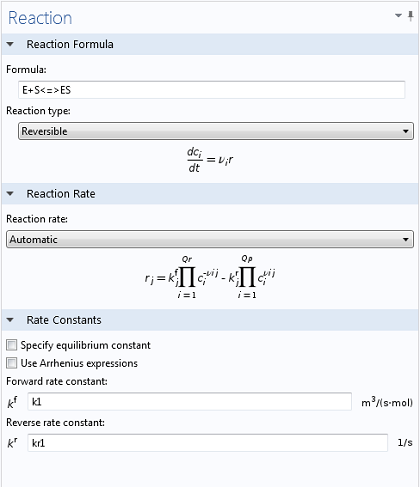
在最初的步骤中,底物S(在本例中是牛肉蛋白)必须与酶E结合。
E + S → ES
这种底物-酶复合物ES也可以根据以下条件再次分离成底物和酶:
ES → E + S
这两个反应通常被写成一个,用可逆反应简略描述为:
E + S ↔ ES
底物不是发生解离,而是在与酶复合时发生反应。随后酶释放出蛋白产物:
ES → E + P
因此,整个系统可以写成:
E + S ↔ ES → E + P
这个反应与上一篇关于化学的博客中的例子密切相关。现在让我们尝试制定这个系统的速率方程。
米氏动力学
底物-酶复合物ES是经过以下过程生成的:
(1)
及其消耗:
(2)
我们现在假设ES(伪)稳态近似(PSSA 或 SSA)。这种常见的近似表明,像酶-底物复合物这样的反应性中间体具有高度反应性。假定消耗ES的反应(解离或反应)比其形成速度快。在这种情况下,我们可以近似地认为ES浓度的变化率可以忽略不计。我们可以这样做,即使ES的浓度可能随着反应的进行而变化;重要的是,在我们感兴趣的反应时间尺度上,ES的浓度对反应物底物S的总浓度变化的响应非常快。
这个近似会产生:
(3)
相当于:
(4)
合并左边的所有项,并将它们归结为一个米氏平衡常数K_\mathrm{M},可以得到
(5)
\,c_\mathrm{ES}=c_\mathrm{E}c_\mathrm{S}
关于系统中存在的酶的浓度,我们知道E的初始浓度,而且我们已经为ES定义了一个变量,所以可以写出:
(6)
将其代入上述公式并求解ES的浓度,就可以得到:
(7)
这个结果可以用来确定蛋白质的产率:
(8)
^0c_\mathrm{S}}{K_\mathrm{M}+c_\mathrm{S}}
这里需要注意的是,在底物浓度高的条件下(通常是在反应尚未进行的情况下),我们可以近似地认为c_\mathrm{S} \gg K_\mathrm{M}。在这些条件下:
(9)
{cat}c^0_\mathrm{E}\equiv v_\mathrm{max}
底物消耗的速度与底物浓度本身无关:它是“零阶”。这个速率只取决于酶的可用浓度,酶会以最快的速度催化底物反应。K_\mathrm{M}和v_\mathrm{max}这两个量被一起用来定义反应系统的动力学。
整个推导过程被称为米氏动力学(Michaelis-Menten mechanism),以 Leonor Michaelis 和 Maud Menten 命名。它被广泛应用在大量生物化学反应中。101 年前,在 Michaelis 和 Menten 发表他们的成果时侯,他们没有机会使用数字计算机来快速整合这四个针对不同物质的微分方程系统。相反,它们通过用一个直观的、以物理学为基础的近似值进行了上述分析,并得到了一个简单的关系式。这个式子显示了酶和底物浓度对酶促反应速率的影响。这个近似的结果如何呢?幸运的是,我们现在可以计算完整的模型,不用假设ES(伪)稳态近似(PSSA 或 SSA),并且可以将结果与简化方程的结果进行比较。
COMSOL 中的酶动力学
使用反应工程接口,可以简单而直观的输入两个相关反应。通过使用 <=> 符号,COMSOL Multiphysics 就立即明白要模拟的是一个可逆反应,为正向和反向速率常数启用必要的输入字段(以及生成E、S和ES的变量)。以同样的方式,一旦输入产生P的方程式,就会创建相应浓度的变量。
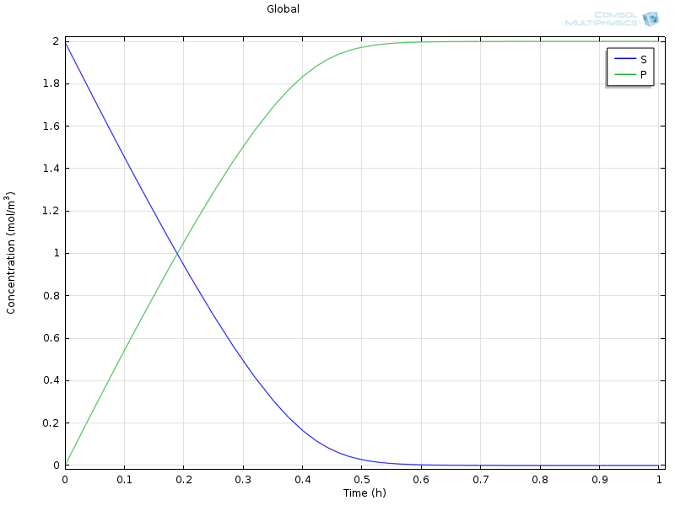
k1= 1700 M-1s-1,k-1= 10-3s-1,kcat= 0.5 s-1,以及E和S的初始浓度的合理值,均取自文献(Calorimetric Observation of a GroEL-Protein Binding Reaction with Little Contribution of Hydrophobic Interaction; K. Aoki et al. J Biol.Chem. vol. 272, pp. 32158-32162, 1997)。由于不同物质的浓度差异很大,两个高浓度的物质(P和S,图1)与高度稀释的物质(E和ES,图2)被分开显示。请注意,这种尺度上的差异本身就证明了使用稳态近似的做法是正确的。
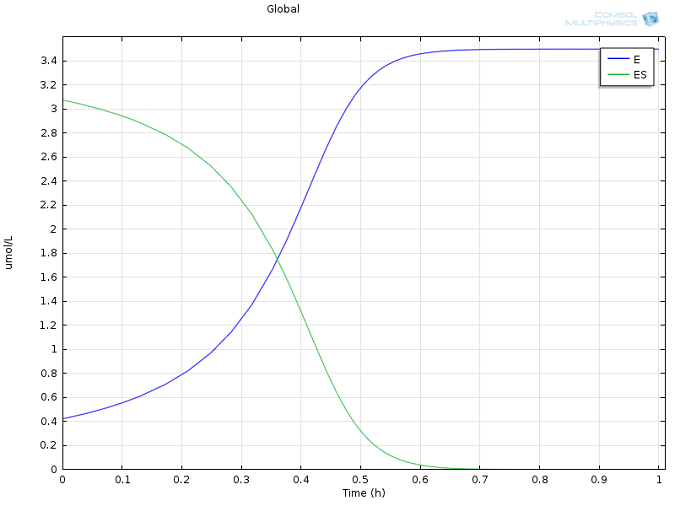
图2:酶(蓝色)和酶-底物复合物(绿色)随时间变化的浓度曲线。
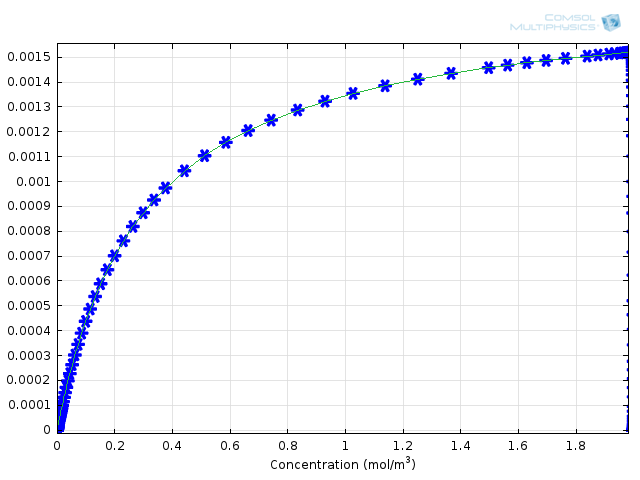
图3:使用米氏动力学近似计算(绿色实线)与使用 COMSOL 完整计算的综合反应(蓝色星号)的结果比较。
结束语
通过这些结果,我们如何了解与米氏动力学有关的误差?我们可以将这些结果与跟产物生成速率公式计算的结果进行比较。为此,我们将 COMSOL 变量comp1.re.r_2(蛋白质的生成速率)和kcat*E0*comp1.re.c_S/(Km+comp1.re.c_S)(导出的米氏表达式)作为底物浓度的函数绘制在同一个 1D 绘图组中。这就产生了上面的图3。您可以看到,近似理论和完整的数值计算方法之间的一致性非常好。
在米氏动力学诞生 100 周年之际,让我们以我们所知道的最好的方式——通过仿真来纪念他们的开创性成果。



评论 (0)