
今天的特邀博主是来自Lightness by Design 公司的Björn Fallqvist,他讨论了超弹性材料分析的不同方法,包括搭接剪切试验和损伤模型。
本系列博文分两部分,本文为第一部分,介绍了一个简单的搭接接头剪切测试,用于确定聚合物的材料参数。第二部分文章将提出一个基于物理学的材料损伤演化规律。
背景介绍
许多软材料,尤其是橡胶和生物组织,它们的应力和应变之间的关系不是线性的,即使在小载荷下也是如此。这些聚合物材料的微观结构导致了它们的非线性行为。例如,在生物聚合物网之类的材料中,聚合物链是缠结在一起的,并且经常交联。宏观材料产生的响应取决于几种不同的机制,其中一种是由热交换引起的细丝滑动、细丝拉直产生的熵刚度和交联刚度(以及粘黏)。
聚合物类材料这种复杂的行为,导致我们经常使用的理想化线弹性材料模型是无效的,因此必须采用不同的建模方法。通常,我们选择超弹性模型来进行建模,模型中的应变能量密度函数用于表征材料的状态和相关的应力。
COMSOL中有多种超弹性函数可供选择的,无论哪种函数,分析都涉及确定至少一个材料参数。这些参数需要通过实验确定,我们之前的一篇博客文章对此进行了详细描述(参考文献1)。然而,通常不同变形状态的数据要么无法获取,要么获取成本很高。
简单的搭接剪切试验可用于确定聚合物的材料参数,接下来我们将对这种方法进行介绍。
超弹性材料建模
假设存在一个应变能量密度函数,我们可以使用此函数对超弹性材料进行建模:
该函数是变形状态的函数,用变形梯度\mathbf{F}表示。
通过将\psi与右 Cauchy-Green 张量\mathbf{C}进行微分,可以得到第二 Piola-Kirchhoff 应力\mathbf{S},然后将其转换为所需的应力状态。
一般来说,\psi可以是控制各种机制的任意数量的内部变量的函数,例如,黏弹性行为和损伤。唯一的要求是这些变量必须满足热力学普遍性规律;即,耗散能必须大于或等于零。
通常,\psi是一个包含许多材料参数的表达式,具体取决于模型的复杂性。在这篇文章中,我们使用了 Yeoh(参考文献2)提出的模型,它包含三个项:
其中,c_1,c_2和c_3,I_1是材料参数,是右 Cauchy-Green 张量的第一主不变量 (\mathbf{C}
)。
许多超弹性材料表现出不可压缩的特性。在计算上,\psi被分成等容和体积部分:
\mathbf{C}的第一不变量I_1被其等容对应项取代。最后一项取决于体积模量K和雅可比J(即,右 Cauchy-Green 张量的第三主不变量)。为了模拟不可压缩性,为K分配一个足够高的值(通常约为剪切模量的 1000 倍)。
进行搭接剪切试验
使用放置在两个较硬的矩形条之间的样品进行搭接剪切试验。试验设置如图 1所示。
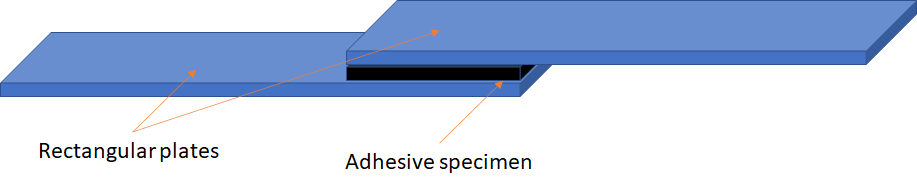
图1.搭接剪切试验。
将两个板水平拉开直到试样破裂,记录力-位移曲线。在这篇博文中,我们分析了一个黏合剂样品。
黏合性能
本文中用作示例的实验数据由Lindhe Xtend AB提供,在此表示感谢。Lindhe Xtend 开发了具有独特的侧向灵活性的假肢 Xtend Foot。侧向灵活性在所有表面上都具有完美的平衡性和稳定性,能让用户在户外和不平坦的地面上移动时获得更大的信心。它减少了用户对跌倒的恐惧,增强了他们自由行走的愿望,并提高了假肢使用者的生活质量。
Xtend Foot 的相关测试数据如下:
- 黏合剂厚度:3mm
- 试样和板的宽度:25mm
- 板厚:5mm
- 黏合剂试样长度:5mm
- 测试温度:20°C
- 位移速率:13mm/min
图 2为所记录力-位移曲线。
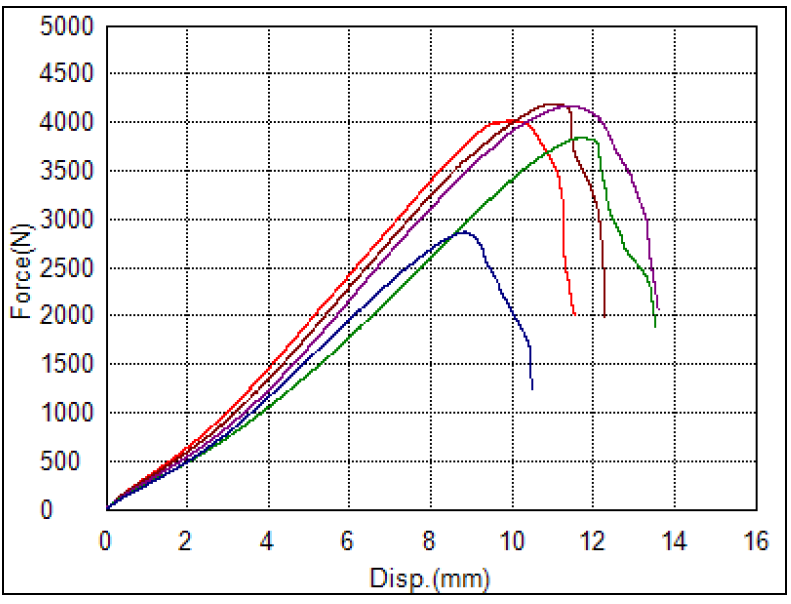
图2.黏合剂的力–位移曲线。
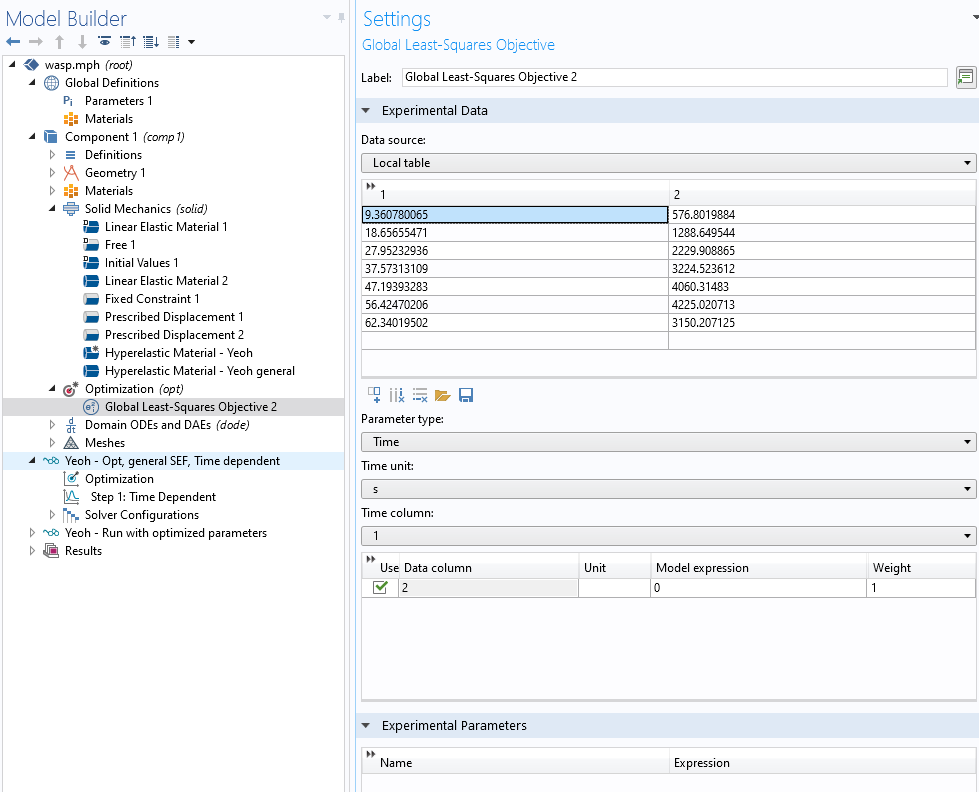
我们选择使用紫色曲线作为测试的基础。在更严格的分析中,我们可以确定一条平均曲线,但对于方法演示,一条曲线就足够了。该曲线表现出初始硬化和由于材料破裂而导致的软化。我们选择了一些点来优化,见表1。
| 位移 [mm] | 力 [N] |
|---|---|
| 2 | 577 |
| 4 | 1289 |
| 6 | 2230 |
| 8 | 3224 |
| 10 | 4060 |
| 12 | 4225 |
| 13.5 | 3150 |
表1.选定的数据点。
计算模型
几何模型
模型的几何结构是在 COMSOL Multiphysics® 软件中使用相关坐标的块几何工具构建的,见图 3。
图3.模型的几何结构。
对这些块进行分区以便于划分网格。由于几何和载荷沿试样和板的长度方向对称,因此只需建立一半模型。
网格
如图4所示,优化方案中的网格特意进行了粗化。
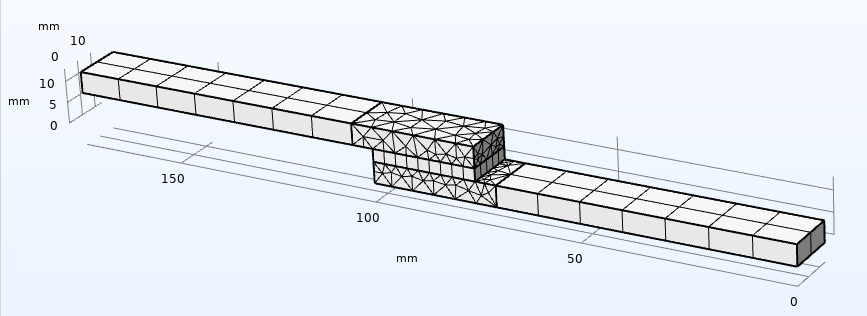
图4.模型网格。
通过扫掠建立外部板域和黏合剂域,连接到黏合剂的板域是用自由四面体网进行网格划分。因为这里我们寻找材料参数的结果是反作用力,所以粗网格是可以接受的。研究黏合剂中的详细应力/应变状态需要进行进一步的细化。
材料模型
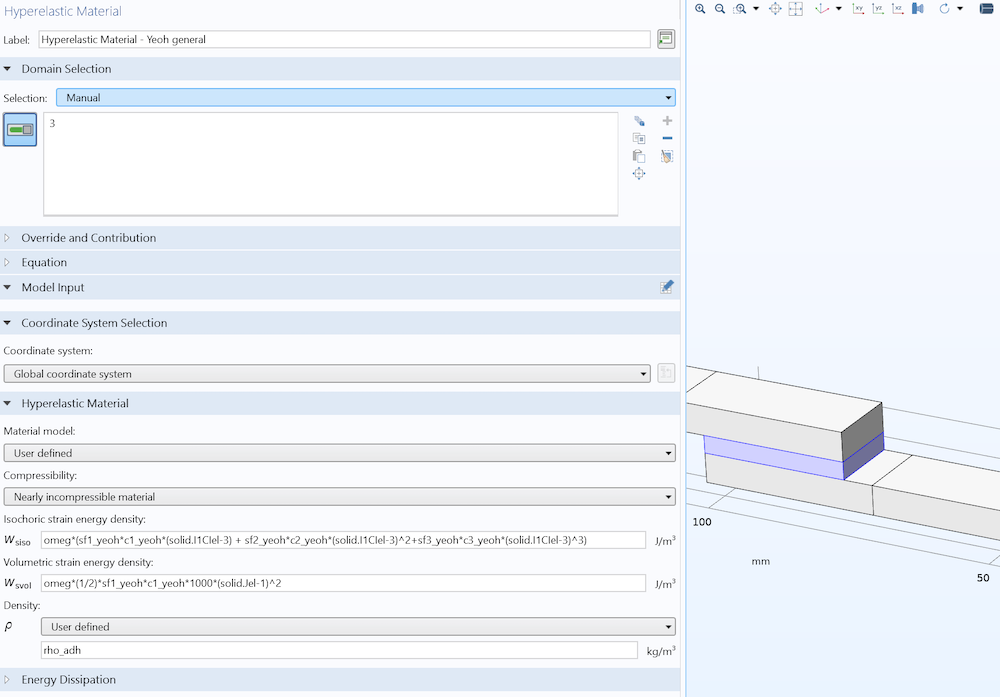
板比黏合剂硬得多,可以认为是刚性的。在这里,我们对其施加了钢的材料特性(杨氏模量 210GPa,泊松比 0.3,密度 7850kg/m3)。Yeoh 模型的超弹性参数c_1,c_2和c_3均设置为 0.1MPa。在材料模型公式中,使用了比例因子来执行简单的优化方案。在 COMSOL Multiphysics 中,材料参数和缩放因子s_{f1yeoh},s_{f2yeoh}和s_{f3yeoh}被定义为参数。
为了便于后续建立损伤模型,我们在超弹性材料定义中使用了用户定义的应变能函数,见图5。
变量“omeg”用于修改应变能密度,稍后我们将对其进行解释。目前,\omega = 1。
边界条件
由于模拟了一半的试样和板,因此沿中心平面应用了对称条件,如图 6 所示。
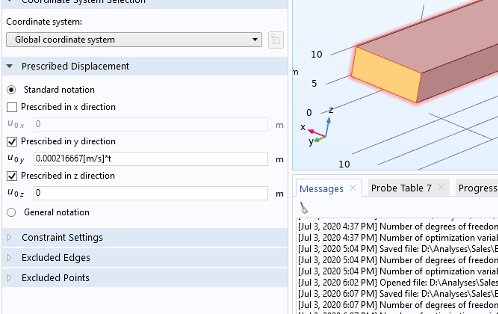
指定试样的一端为固定约束,另一端指定为与时间相关的位移的函数,如图 7 所示。
图7.板端面的边界条件。固定约束(左)和指定位移(右)。
研究类型和优化设置
由于损伤模型是基于速率形式的常微分方程建立的,因此使用瞬态研究进行求解。对于超弹性模型,稳态研究就足够了。
对现有的材料数据进行优化,需要我们定义在每个时间步长上所施加的与位移相对应的反作用力。因此,我们必须对指定的位移设置启用弱约束,并将其合并到表面上,如图 8 所示。第二个原因是我们只对几何的一半进行了建模。
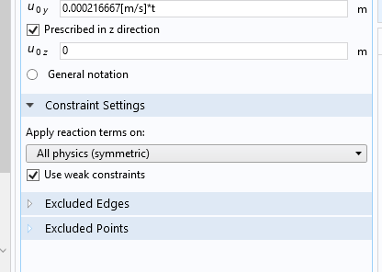
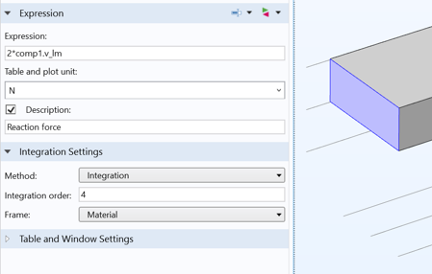
图8.优化反作用力的定义。
接下来,我们定义一个具有全局最小二乘目标的优化节点,见图 9。
由于我们使用瞬态求解器进行求解,因此必须使用图 7 中定义的变形率将表 1 中的位移转换为第一列中的时间。对纯超弹性模型的第一次分析,我们仅使用前三个点,因为下一篇博客里对软化过程需要更复杂的分析。
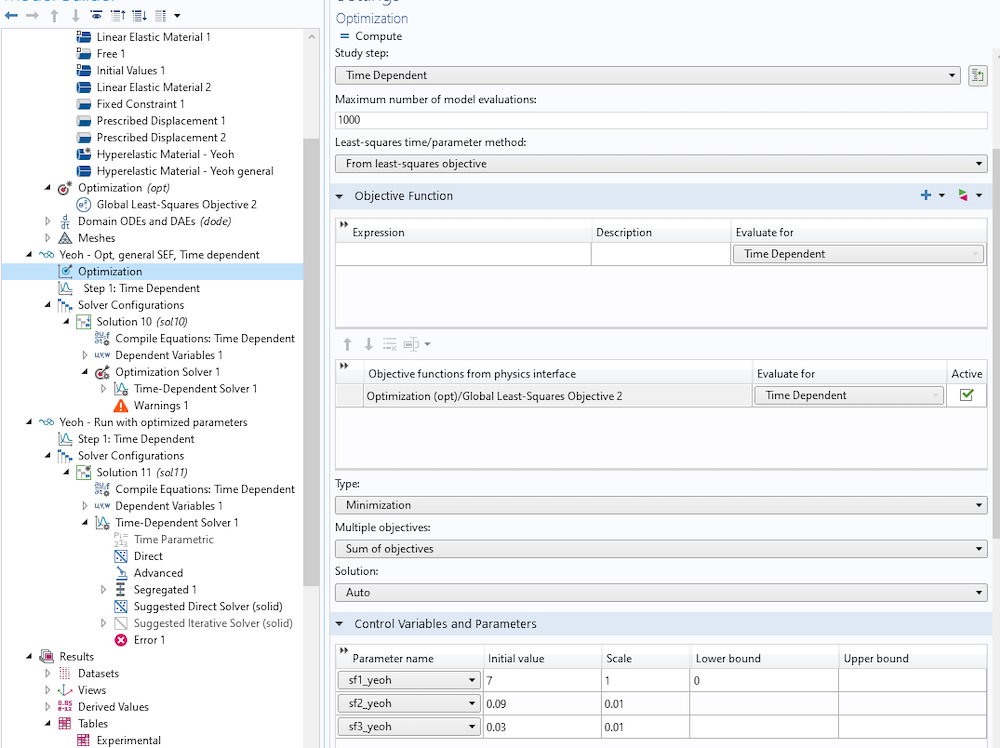
最后,我们定义一个瞬态研究并插入一个优化节点,见图 10。
我们对三个比例因子进行了优化,它们参与对超弹性材料模型定义中材料参数的缩放作用。唯一的限制是s_{f1yeoh}必须是非负的,因为它会缩放剪切模量。为了在求解过程中跟踪缩放参数的值,可以方便地定义它们的全局变量探针。这样就会把它们储存在探测表中以进一步使用。
要定义一项使用优化参数分析的研究,只需要创建一个新研究并将求解的变量值设置为之前的解,如图 11 所示。
结果:网格的位移和影响
变形图与所选的材料参数无关,如下图 12 所示,用于直观的显示分析结束时的状态。
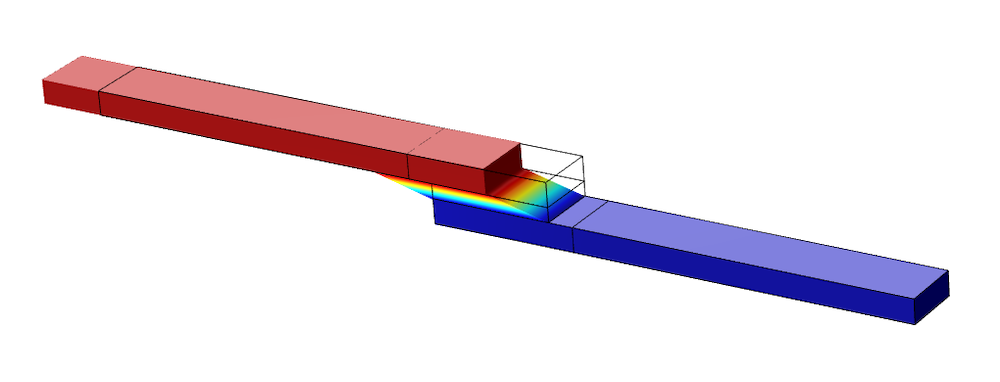
图12.分析结束时模型的变形。
如前所述,网格会影响应变状态。我们还对精细化模型进行了分析(没有损坏),如图 13 所示。
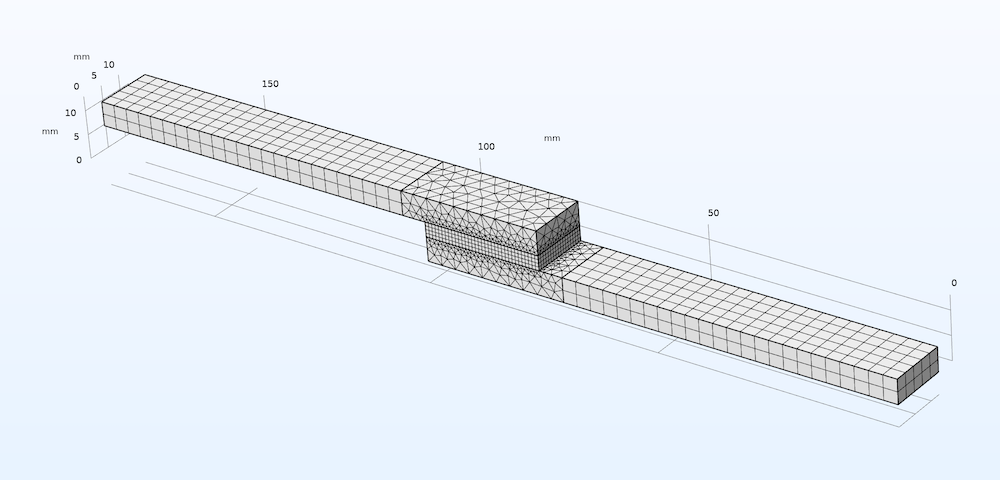
图13.细化的模型网格。
图 14 显示了第四个数据点 (8 mm) 处的黏合剂域中的第一主应变。
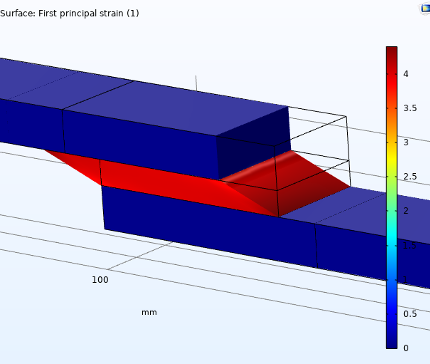
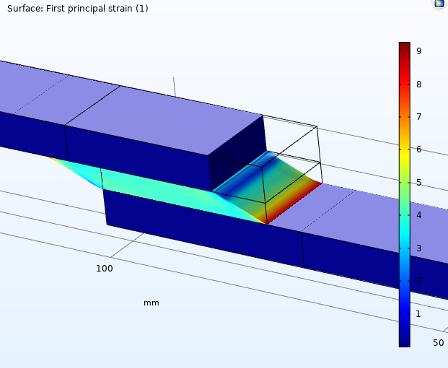
图14.黏合剂域中的第一主应变,未精细化(左)和精细化后(右)。
可以看出,细化模型中的应变值要高得多,未细化模型中没有明显的梯度变化。分析过程中应变的最大值如图 15 所示,显示反作用力是为了表明网格细化不会影响它的值。
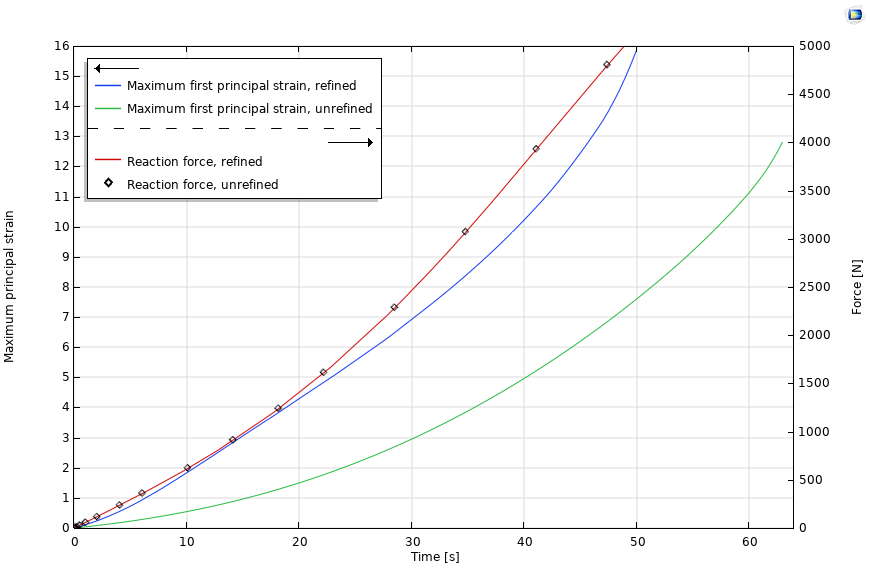
图15.黏合剂域中的最大主应变和反作用力。未细化和细化的网格结果。
结果:优化超弹性模型的材料参数
材料参数及其优化后参数的总结,如表2 所示。
| 缩放参数 | 初始值 [-] | 优化值 [-] |
|---|---|---|
| s_{f1yeoh} | 7 | 6.56 |
| s_{f2yeoh} | 0.09 | 0.34 |
| s_{f3yeoh} | 0.03 | -0.0072 |
| 最小二乘目标 [N2] | ||
| 1.28e-14 |
表2. 初始和优化缩放和材料参数;无损伤。
产生的力-位移曲线如图 16 所示。
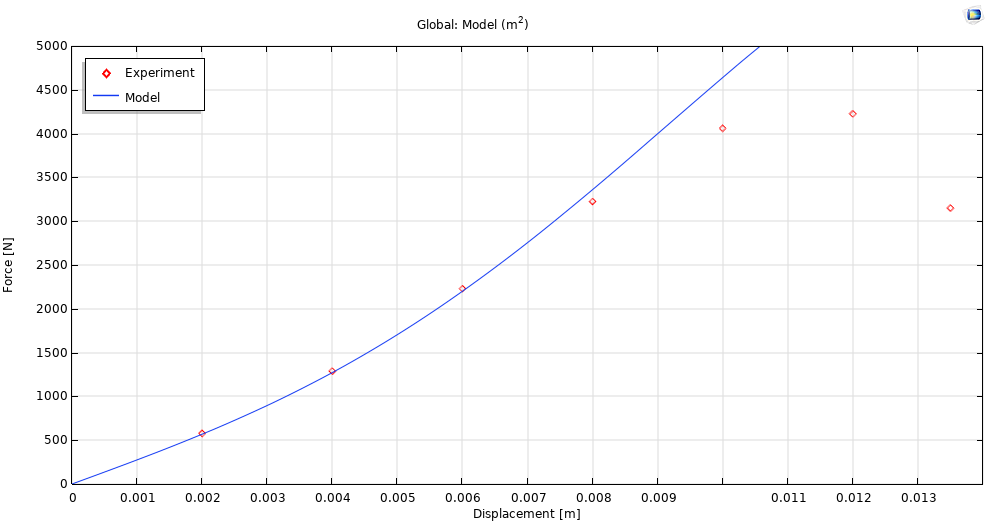
图16.超弹性模型的力–位移曲线。
可以看出,在材料软化之前,Yeoh 模型预测结果与试验数据具有极好的一致性。
敬请关注
接下来的博文中,我们将为材料提出基于物理学的损伤演化定律,该定律容易实施,并结合了材料软化(单调和循环加载)、蠕变和循环过程中滞后曲线的稳定。
敬请关注本系列博客的第 2 部分内容。
关于作者
Björn Fallqvist 是Lightness by Design 公司的一名顾问,从事基于数值分析的产品开发工作。他于 2016 年获皇家理工学院博士学位,致力于开发本构模型以捕捉生物细胞的机械行为。他的主要专业兴趣是材料表征领域,专长是使用各种材料模型描述物理现象。
参考资料
- C. Kumar, “通过各种超弹性材料模型对测量数据进行拟合“,COMSOL Blog, 2015.
- O.H. Yeoh, “Some forms of the strain energy function for rubber”,Rubber Chemistry and Technology, 5, vol. 66, pp. 754–771, 1993.



评论 (2)
昊 金
2022-10-05Hello, Prof. Björn Fallqvist! I am doing tensile test simulations and it was very inspiring to see your blog. Could you send me your COMSOL model for study? I would be very grateful if you could. This is my email102010127@hbut.edu.cn. Thank you!
Hao Li
2022-10-10 COMSOL 员工您好,此模型是作者所有,我司无法提供。
该篇博客中已经详细说明了建模过程,您可以模仿此博客进行建模。
若在建模过程中遇到问题可以使用技术支持,网址如下:
//www.denkrieger.com/support