利用对称性简化磁场建模

每当使用 AC/DC 模块对稳态、瞬态或频域中的磁场进行建模时，我们都希望尽可能减小模型的大小，以最大限度地减少求解模型所需的计算资源和时间。今天，我们将介绍可以在建模中利用的三种对称边界条件，并演示如何使用它们。

使用三个对称平面对线圈进行建模

首先，我们来看一个矩形绕制的多匝线圈，如下图所示。球形建模域包含一个矩形线圈。线圈域代表围绕矩形轮廓缠绕的数百匝导线。模型中忽略了激励线圈的引线，我们将线圈视为电流的闭环。多匝线圈特征用于计算和施加围绕线圈轮廓均匀分布的电流，并绘制稳态磁场。请注意，沿线圈周围的电流路径的线圈域具有恒定的横截面积。

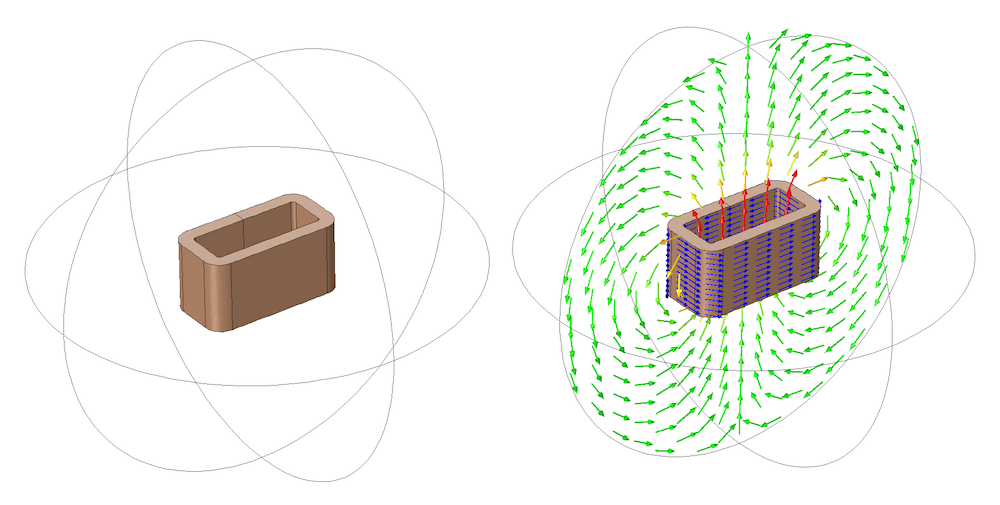
电流沿绕组方向流动的矩形线圈。绘制了电流（蓝色箭头）和磁场。

这个建模域有三个对称平面，即平面的几何是完全镜像的。现在，让我们来看看如何利用这种几何对称性，以及我们所掌握的磁场和电流流动方向的知识来减小建模域的大小。

磁绝缘边界条件

用磁绝缘边界条件表示磁场的镜像对称面。当穿过该平面时，磁场会被完全镜像。

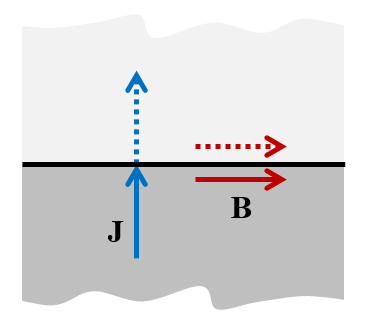
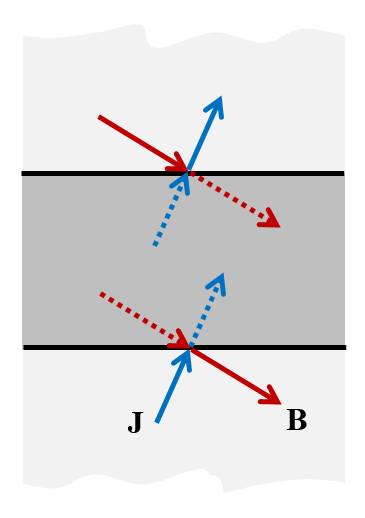
磁绝缘边界条件——模型几何边界的切线垂直于J并与B平行。

这个边界条件也意味着磁场在边界的法线方向上为零。也就是说，磁场必须与该边界相切。因此，该边界条件具有边界的物理解释，电流只能沿法线方向流过该边界。建模法则可以概括为：“用磁绝缘边界的切线垂直于J并平行于B。”

完美的磁导体边界条件

另一方面，用完美磁导体边界条件表示电流的镜像对称平面。从数学的角度来看，它可以被认为是磁绝缘边界条件的“对立面”。

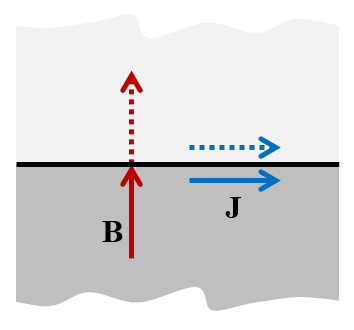
完美磁导体边界条件——“模型几何边界的切线垂直于B并平行于J”。

当穿过平面时，电流矢量会完全镜像，并且没有法向分量，所以电流一定是切向流动的。这个边界条件使磁场在接近边界时，没有切向分量，所以磁场只能指向法线方向，当越过边界时，磁场不会改变符号。其建模法则可以概括为:“使用完美磁导体的边界的切线垂直于B，平行于J进行”。

简化线圈模型

原始几何体的大小可以缩小到代表原始几何体的八分之一模型。通过线圈中心的正交平面用于划分域，如下图所示。

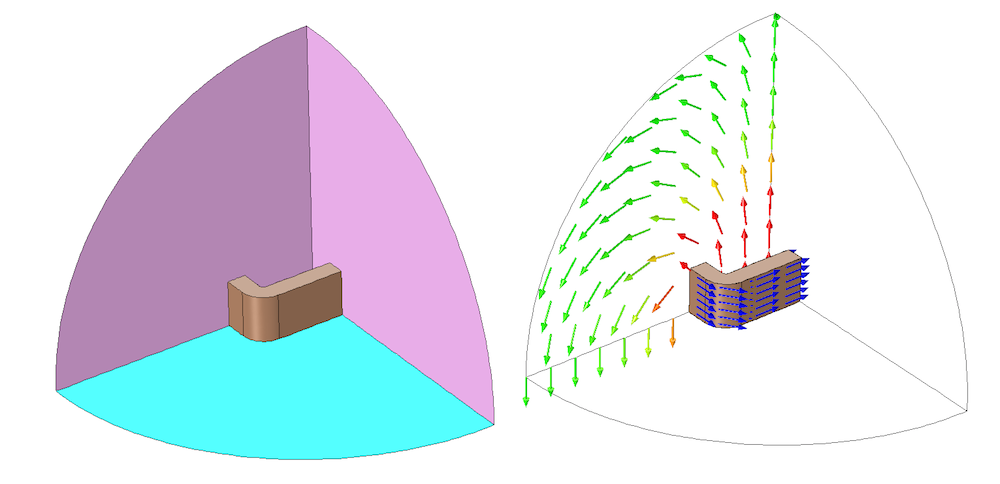
电流沿绕组方向流动的矩形线圈的八分之一对称模型。在这个问题中，沿对称平面应用了磁绝缘（洋红色）和完美磁导体（青色）边界条件。

磁绝缘边界条件施加在表示电流正常流过的平面的两个边界。如果线圈在电压边界条件下被激励，那么对于施加的每个磁绝缘对称条件，将电压降低两倍很重要。如果线圈用电流激励，就不需要改变施加的电流，但对于每个磁绝缘对称条件，后处理的线圈电压应该按两倍缩放。

完美磁导体条件用在电流沿切向流动的平面。由于完美磁导体条件将线圈切成两半，因此在使用电流激励时将施加的电流分成两半很重要。另一方面，如果使用电压激励，对于每个完美磁导体对称平面，后处理的线圈电流必须放大两倍。

周期性(边界)条件

在几乎所有情况下，磁绝缘和完美磁导体边界条件足以显著减小模型的大小。正如我们在前面看到的，这些条件强制电流和磁场与边界垂直或相切。但是，如果我们有一个几何对称平面，但场没有这种对称性呢？在这种情况下，周期性(边界)条件可能是合适的。

当我们只知道解必须是周期性时，使用周期性条件。

周期性(边界)条件允许更一般的对称性，其中电流和磁场矢量都可以与边界成一定角度。这个条件的使用仅限于磁源和结构在空间中具有周期性的情况。通常，整个几何结构可以简化为最小的重复单元，即受周期性条件限制的单位单元。

以用单股线缠绕的环形电感器的结构为例，如下图所示。只要我们再次忽略由于引线引起的不对称性，导线就可以相当准确地被建模为围绕环形的单个连续螺旋。我们可以将导线建模为沿导线切向流动的边缘电流。

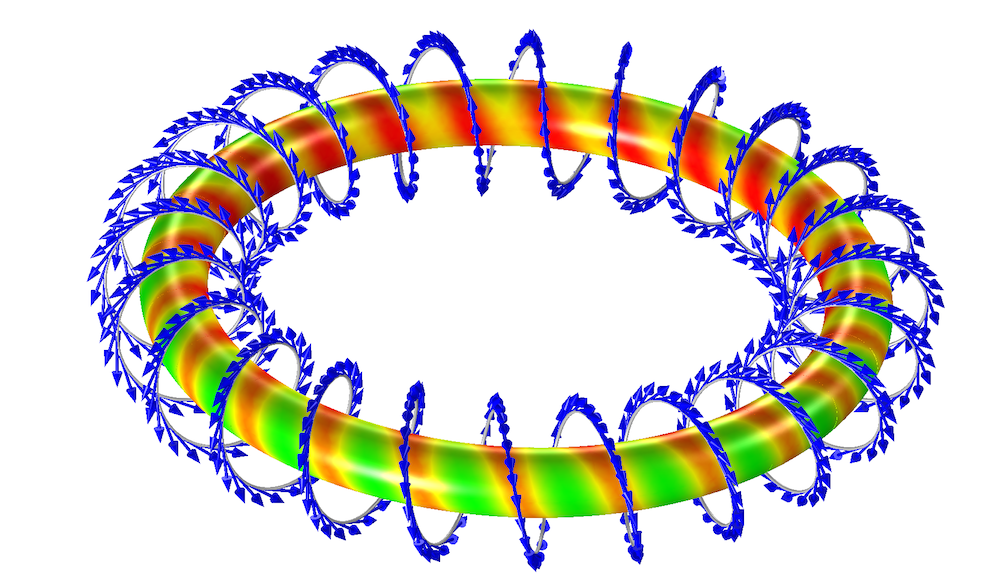
螺旋缠绕的环形电感器。箭头(蓝色)表示电流的方向。显示了核芯中的磁场。

为了尽可能多地利用对称性，我们可以考虑只有一圈绕组的原始模型的一小片单元。周期条件用在沿切片的两侧。当使用这个边界条件时，周期性面上的网格必须是相同的，所以应该使用复制面功能来确保相同的网格。从下图中我们可以看到，模型的尺寸可以通过绕组的数量来减小，这大大减小了问题的大小。

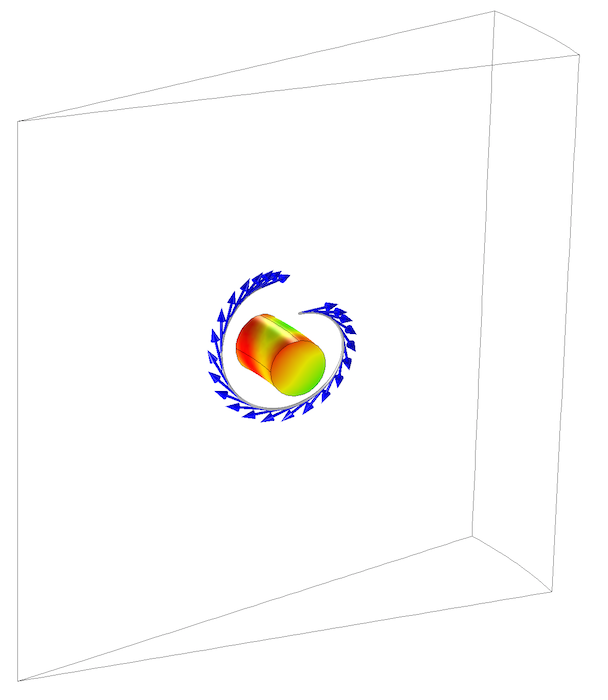
周期性条件可以大辐减小了某些几何形状的模型大小。

与更基本的磁绝缘和完美磁导体条件相比，周期性条件的普遍性是有代价的。由于它将几何结构一侧的未知场与另一侧的未知场联系起来，这使得系统矩阵更加密集，并且求解成本更高。因此，如果更基本的条件适用，请不要使用它。

总结

通过减小模型大小，我们还大辐降低了计算要求。事实上，计算需求随着问题的大小呈指数增长，所以可以使用的对称性越多越好。即使在要解决的整个问题中没有对称性，通常建议在建模的初始发展阶段使用确实具有对称性的一个较小的模型。

下一步

想了解更多关于对称边界条件的信息？通过下面的按钮联系我们：

• 如果你想练习您的建模技能，可以查看以下这些相关的教程模型：
  • 铁板的磁力变形
  • 发电机三维建模
  • 电源开关的电动力学
  • 矢量滞回建模

编者按：本博客于 2022 年 8 月 31 日更新，讨论了 COMSOL Multiphysics^®软件 6.0 版本中的一项新功能。