
当敲击音叉(注:音叉是一种常用的物理实验器材,敲击后可以产生单一波长的机械波)并将其放置在桌面上时,发出声音的峰值频率会加倍——这一神秘的现象令许多人感到困惑。在这篇博客文章中,我们将通过仿真来解释音叉的奥秘,并在此过程中提供一些与音叉有关的有趣事实。
音叉之谜
Standupmaths 在 YouTube 上发布的一条视频中,科学爱好者 Matt Parker 和 Hugh Hunt 讨论并演示了关于音叉的“奥秘”:当敲打音叉并将其放在桌面上时,发出声音的频率似乎加倍了。事实上,这个谜团可以用非线性固体力学来解释。
声音如何到达我们的耳朵?
当我们用手握住振动音叉时,叉齿的弯曲运动会使周围的空气流动。空气中的压力波以声音的形式传播。我们可以听到这个声音,但这不是将机械振动转换为声压的有效转换。
当我们将音叉的柄部放在桌子上时,柄部的轴向运动将连接到桌面。该运动比音叉的横向运动小得多,但它有可能使桌面运动—与音叉的细叉齿相比,大且平整的桌面发出声音的效果要好得多。此时,桌面表面充当了较大的扬声器振膜。

音叉。
为了研究这种有趣的现象,我们创建了音叉的固体力学计算模型。该模型是基于我的一个同事的音叉设计的。这个音叉的参考频率为 A4(440 Hz),材料为不锈钢,总长度约为 12cm。
首先,让我们看一下音叉在其第一阶特征模态下振动时的位移:

音叉基频的振型。
如果我们详细研究位移,会发现即使音叉的整体运动是横向的(图片中的 x 方向),也有一些小的垂直分量(在 z 方向上),包括两部分:
- 音叉的弯曲伴随着在音叉横截面上线性变化的上下运动
- 如牛顿第二定律所要求的,柄具有基本刚性的轴向运动,这对于将质心保持在固定位置是必要的。
位移结果如下图所示。将该模式归一化,以使最大总位移为 1。轴向位移峰值为 0.03,柄的位移为 0.01。
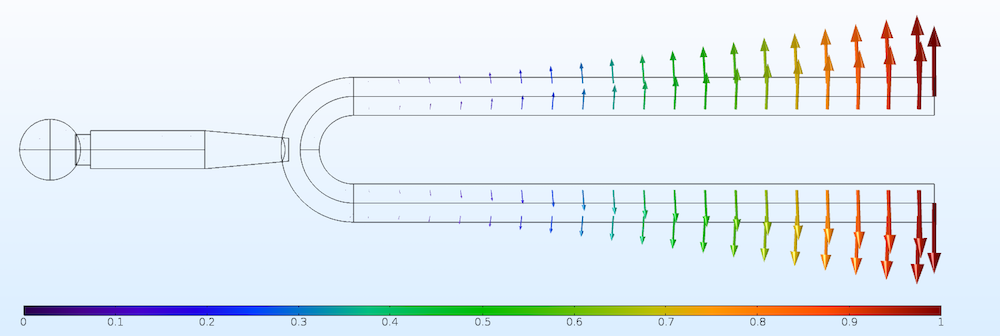
第一阶特征模态的总位移矢量。
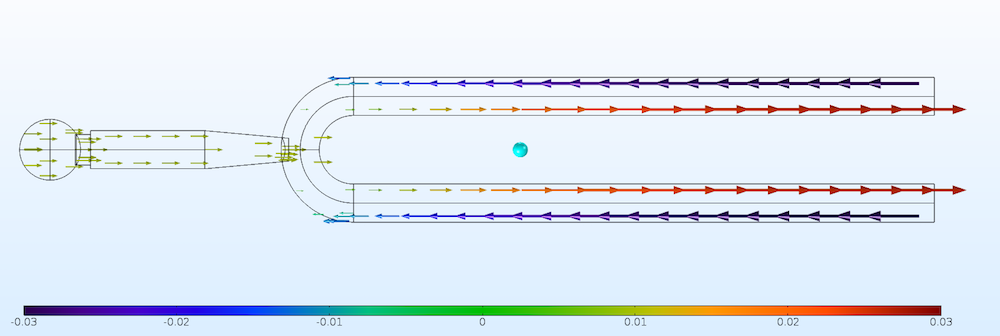
仅轴向位移。注意,数字之间的比例不同。重心由蓝色球体表示。
现在,我们来看一下声音的发射。通过在模型中加入声场的边界元表示,可以计算周围空气中的声压级。音叉尖端的振动大小被设置为 1mm。如果从应力的角度看音叉不过载,那么这可能是最大可行值。
如下图所示,声音强度随着距音叉的距离增大而迅速降低,并且具有很大的方向性。实际上,如果在耳朵旁将音叉绕着音叉轴旋转,我们会惊奇的发现在 45 度方向上几乎没有声音。
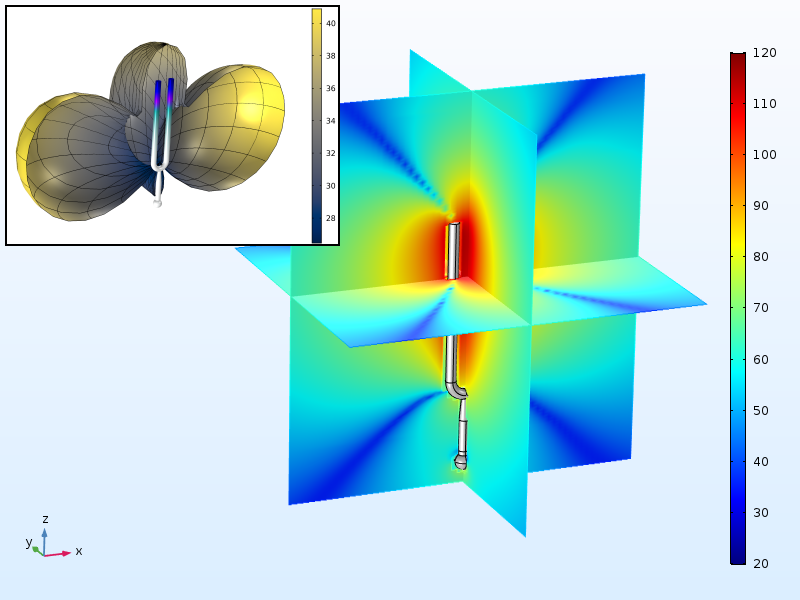
音叉周围的声压级(dB)和辐射方向图(插图)。
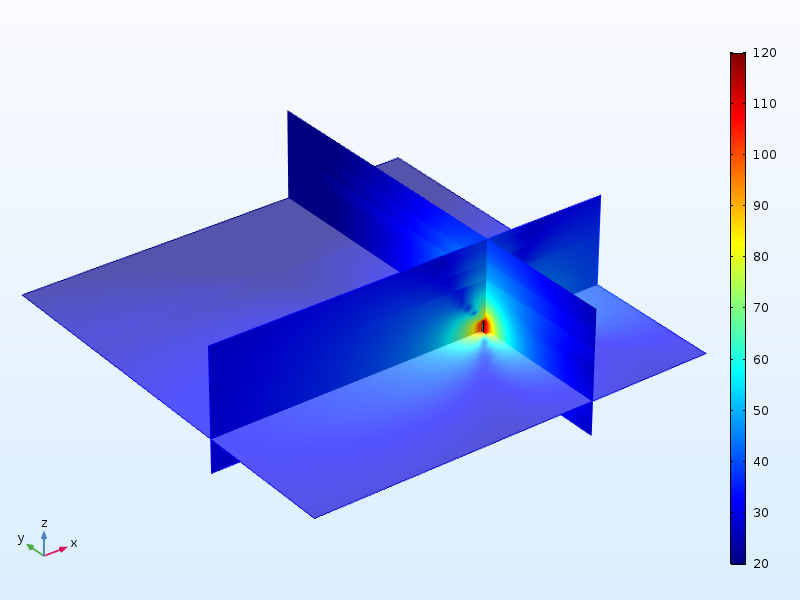
现在,我们向模型添加了一个 2cm 厚的木桌表面。它的尺寸为 1mx1m,并在拐角处有支撑。音叉的柄与桌子中央的一点接触。如下图所示,在桌面上方和外部的大部分空气域中,声压级非常重要。
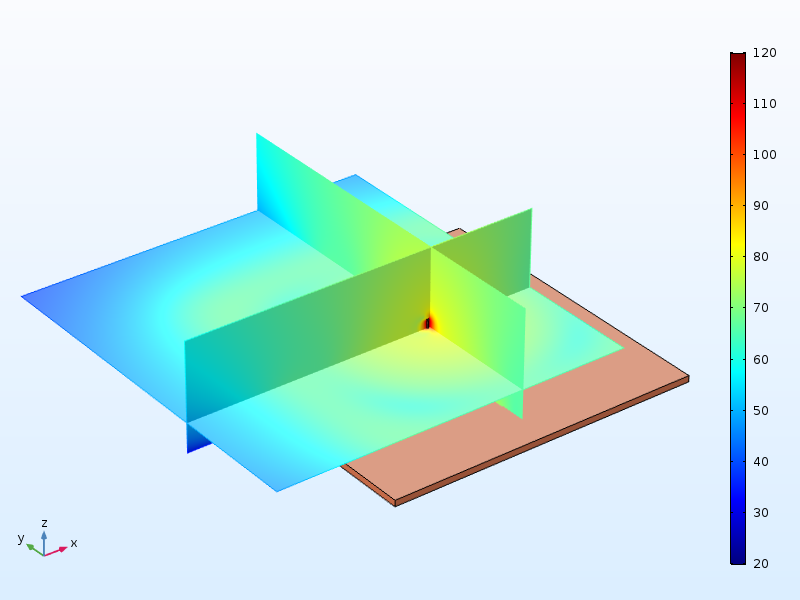
将音叉的柄连接到桌面时,桌面上方的声压级。
为了进行比较,我们绘制了音叉被举起时相同空气域的声压级。除了音叉附近,桌子上方所有空气部分都具有非常低的声压级,这种差异非常惊人。这与我们在 YouTube 原始视频中使用音叉的经验相符。
抬起音叉时桌面上方的声压级。
倍频是固有频率吗?
到目前为止,我们还没有回答文章开头的问题:将音叉放在桌子上时,为什么频率加倍?一种可能的解释是,存在这样的固有频率,其运动在垂直方向上更突出。例如,对于振弦,固有频率是基频的整数倍。
但音叉不是这种情况。如果音叉在弯曲时近似为悬臂梁,那么最低固有频率可以用下面的表达式给出,
此表达式中的物理量为:
- 音叉长度,L
- 杨氏模量,E;钢通常约为 200GPa
- 质量密度,ρ;约 7800kg/m3
- 音叉横截面的面积惯性矩,I
- 音叉的横截面积,A
对于我们的音叉,其评估值为 435Hz,因此该公式提供了一个很好的近似值。
悬臂梁的第二阶固有频率为,
该频率比基频高出 6.27 倍。它不是倍频。但是,除了具有对称弯曲的振型外,还有其他振型。这其中一个会是倍频吗?
因为存在两个原因,所以这不太可能。第一个原因是,对于具有不同几何形状的音叉,可以观察到倍频现象,但如果所有音叉的特征模态都正好是基本固有频率的两倍,那就太巧合了。第二个原因是非对称特征模态在被紧握的音叉柄上有明显的横向位移。这样的特征模态将被我们的手强烈地减弱了,并且有一个不明显的振动幅度。下面的动画中显示了一种这样的模式,其固有频率为1242 Hz。
音叉的第一阶特征频率为 440Hz,特征频率为 1242Hz 的面外模态,第二阶弯曲模态的特征频率为为 2774Hz 。
音叉之谜的可能原因
让我们总结一下我们对倍频现象的了解。由于只有在将音叉按到桌面上时才会出现这种情况,因此双频振动在柄中具有很强的轴向运动。此外,从频谱分析仪(可以在智能手机上下载这样的应用程序)中我们可以看到,双频振动水平衰减得相对较快。有一个过渡回到基频作为主导频率。
对幅度的依赖性表明存在非线性现象。柄的轴向运动表明柄补偿了叉齿质心位置的变化。
无需赘述数学原理,可以看出,对于弯曲悬臂梁,质心相对于原始长度L向下移动了一段距离,即
其中,a是尖端的横向运动,系数 β≈0.2。
一个重要的观察结果是,质心的垂直运动与振幅的平方成正比。同样,质心在每个周期两次位于最低位置(叉齿向内弯曲和向外弯曲时),因此是双倍频率。
当 a = 1mm 且叉齿长度为 L=80mm 时,叉齿质心位置的最大偏移可估计为,
柄的质量比叉齿的质量小得多,因此必须移动更大的位置才能使整个重心的位置保持不变。因此,柄的位移幅值可以估计为 0.005mm。我们应该从上面的数值实验中了解到了这一点。轴向运动的线性(440 HZ)部分的数量级为 a/100; 在此示例中为 0.01mm。
实际上,音叉是一个比纯悬臂梁更复杂的系统,并且柄和音叉之间的连接区域会影响结果。对于此处分析的音叉,二阶位移实际上小于预测的 0.005mm 的后包络的一半。
尽管如此,由二阶运动质量效应引起的轴向位移仍然很大。此外,在发出声音时,重要的是速度而不是位移。因此,如果位移振幅在 440Hz 和 880Hz 时相等,则倍频时的速度是基频时的两倍。
由于在 440HZ 的轴向振动的振幅正比于叉齿振幅 a,并且 880Hz 的振动的幅度正比于a^2,因此我们有必要用力敲击音叉以体验倍频效应。随着振动衰减,非线性项的相对重要性降低,在频谱分析仪上可以清楚地看到这一点。
可以通过执行几何非线性瞬态动力学分析来详细研究其行为。通过水平施加在叉齿上的对称脉冲使音叉自由振动。可以看出,水平叉齿的位移在 440Hz 时几乎是正弦曲线,而柄以明显的非线性方式上下运动。柄位移是高度非对称的,因为 440Hz 的贡献与叉齿位移同步,而 880Hz 的项始终会产生额外的向上位移。
由于系统的非线性,振动不是完全周期性的。即使是叉齿位移幅值也可能随着周期变化。
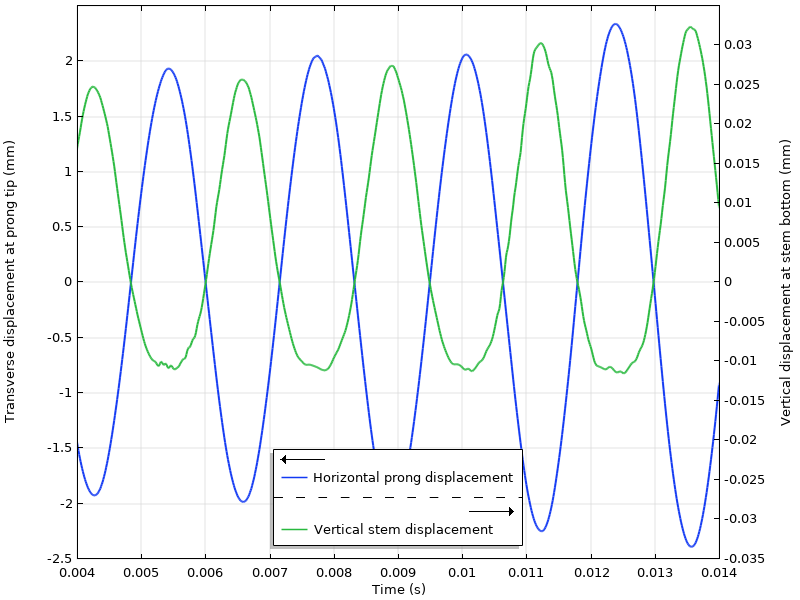
蓝线显示叉齿尖端的横向位移,绿线显示柄底部的垂直位移。
如果上面绘制的柄位移频谱是通过 FFT 计算的,则在 440Hz 和 880Hz 处有两个明显的峰值。在第二弯曲模态附近还有一个小的第三峰。
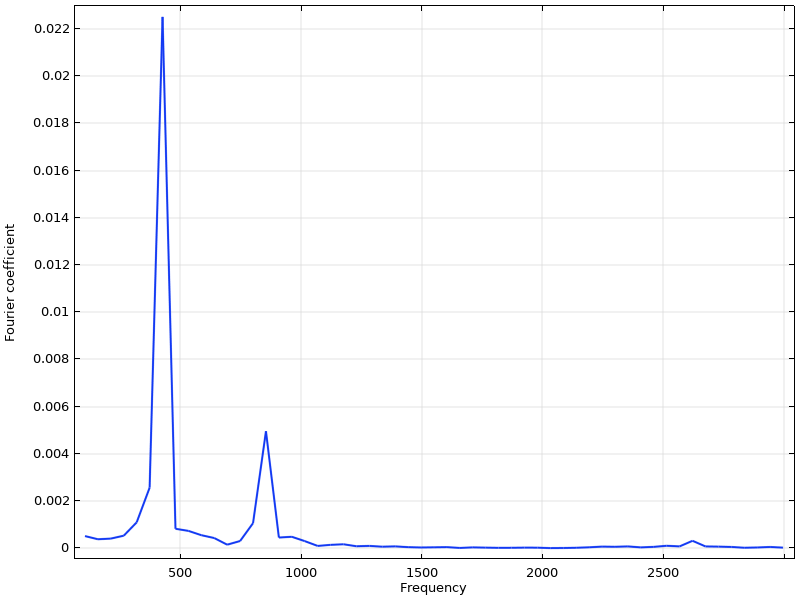
垂直柄位移的频谱。
要实际查看 880Hz 下的二阶项,我们可以从柄总位移中减去与叉齿弯曲同相的柄振动部分。如下图所示,该位移差显示为红色曲线。
总轴向柄位移(蓝色),叉齿弯曲比柄位移(绿色虚线)和其余的二阶位移(红色)。
我们如何执行此计算?从特征频率分析中我们知道,轴向柄振动的幅度约为横向叉齿位移的 1%(实际上为 0.92%)。在上图中,绿色虚线是叉齿顶端当前位移的 0.0092 倍(图中未显示)。该曲线可以看作是显示了 440Hz 的线性项-或多或少的纯正弦波。然后从总柄位移中减去该值,剩下的是红色曲线。当叉齿笔直时,二阶位移为零,并且当叉齿具有最大向内弯曲和最大向外弯曲时,二阶位移达到峰值。
实际上,红色曲线看起来非常像是有一个与 sin2(ωt)成正比的时间变化。根据上面的分析,该位移应与叉齿位移的平方成正比。使用众所周知的三角函数,\sin^2(\omega t) = \dfrac{1-\cos(2 \omega t)}{2}。输入倍频!
不同的音叉
standupmaths 的原始视频的评论者已经注意到,某些音叉的效果比其他音叉好,而对于某些音叉,很难看到频率加倍。如上所述,第一个标准是您要用力敲击以进入非线性状态。但是,也存在影响两种振动幅度之间比率的几何差异。
例如,为了保持重心,柄必须移动得更多,因此相对于柄较重的叉齿会引起较大的倍频位移。细长的叉齿可以具有更大的振幅-长度(a/L)比,从而增加非线性项。
叉齿与柄相交的区域的设计很重要。如果是刚性的,则柄中的基频振动的幅值将减小,并且倍频振动的相对重要性更大。
叉齿的横截面也会产生影响。如果我们返回固有频率的表达式,
可以看出,截面的惯性矩起到了作用。带有d边的方形横截面的叉齿具有
而直径为d的圆形横截面的叉齿具有
因此,对于从侧面看时相同的两个音叉,具有方形轮廓的音叉必须具有长 1.14 倍的叉齿才能提供相同的基频。如果假设由于两个音叉的弯曲而产生的最大应力相同,则具有方形轮廓的音叉具有较高的承载能力,因为其横向位移幅值会比圆形音叉的横向位移幅值大 1.142 倍。此外,如果将柄保持在固定尺寸,则与较长的叉齿相比,它将成比例地变轻。当从圆形轮廓移动到方形轮廓时,所有这些贡献最终导致垂直柄振幅增加了 70%。
另外,具有圆形横截面的音叉的设计通常在叉齿和柄之间的连接处更加灵活,因此在基频处具有更高的振动水平。
结论是,具有方形横截面的音叉比具有圆形横截面的音叉更有可能表现出倍频特性。
我们听到频率加倍了吗?
在大多数情况下,答案是“否”。即使基频的幅值可能比倍频的幅值低,但基频仍然存在。但是,尽管音色不同,但我们的感官工作方式却听到了基频。很难如此用力地击打音叉,以使倍频的声压级明显占主导地位,但这并非不可能。
结论
倍频是由于非线性现象而发生的。在该现象中,音叉的柄必须向上移动,以补偿当叉齿接近其弯曲运动的最外侧位置时叉齿质心的小幅度降低。
请注意,并不是音叉连接到桌面上导致频率加倍。在这种情况下,我们对其进行测量的原因是,共振台表面发出的声音是由轴向柄的运动引起的,而我们从竖起的音叉中听到的声音则主要是由叉齿弯曲引起的。在这两种情况下,只要忽略工作台表面的阻抗,其运动是相同的。实际上,当音叉被按住时,您也可以测量出倍频,但是它比基频低30 dB左右。
后续步骤
- 在 YouTube 上观看 standupmaths 的原始视频:
- 在 COMSOL 博客上了解有关音叉和仿真的交集的更多信息:



评论 (0)