用阿伦尼乌斯方程描述化学反应动力学

化学反应工程是一个有趣的建模挑战。乍一看，描述一个反应系统似乎非常容易。然而，仍然存在无数的复杂情况和陷阱，使化学模拟既有挑战性又有意义。在这篇博客中，我们将对化学动力学进行整体介绍，并指导如何使用 COMSOL 软件模拟化学反应工程。

化学动力学简介

毫不夸张地说，化学非常重要。任何生物系统的运作都离不开化学反应。任何时候我们想要影响生物系统，无论是酿造啤酒还是使用止痛药治疗头痛（可能与啤酒有关），实际上就是在对化学反应过程起作用。但是，化学不仅是生物学的基本原理，它对我们现代社会的方方面面也至关重要。从溶剂、颜色、燃料、油漆到塑料和杀虫剂，工业生产的化合物超过 7 万种。因此，化学工业是全球经济的一个最大贡献者也不足为奇了。据估计，化学工业产品的总价值每年近 5 万亿美元，相当于世界总产值的 7% 左右。

一个简单的化学反应实例

我们来看一个例子。某种物质\mathrm{A}（称为反应物、底物或原料）转化为另一种理论上更有价值的物质（被称为产物），可以用反应方程来表示：

即使这个方程没有说明反应的机理（即化学键断裂和形成的顺序，以及哪些中间化学物质是瞬时产生的），我们仍然可以用数学方法描述宏观的反应速率。为了更好地理解宏观反应速率的概念，我们来设想一个虚拟的实验。让物质 A 在烧杯中反应，间隔取一个固定体积的样品，然后把这个样品放入一个分析装置中，通过某种方法可以计算出样品中存在的\mathrm{A}和\mathrm{B}的粒子数量。测量粒子数量并将其除以样品体积实际上等同于测量样品的浓度。

浓度通常用单位 mol/L 或 mol/m³来描述。摩尔是“物质的量”的单位，也可以写作N_A，表示原子、分子、电子或我们要测量的任何物质的简称。这样表示很方便，因为实际样品中出现的分子量非常大；阿伏伽德罗数N_A，代表非常大的分子量（大约为 6×10²³/mol）。

回到我们的虚拟实验，我们可能会观察到如下图所示的行为：

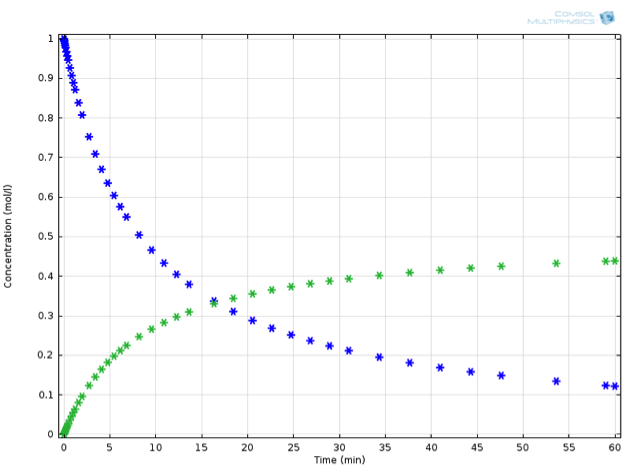
浓度随时间的变化曲线：物质 A（蓝色）减少，物质 B（绿色）增加。请注意，A 的减少速度是 B 增加速度的两倍。

我们能不能提出一个数学表达式来描述化学反应的速率？随着反应物浓度的增加，反应速率很可能也会增加，但是增长比例是多少？一个建议是使用质量作用定律来描述，它将化学反应想象成由于反应物之间的碰撞而产生的。我们提出，\mathrm{A}的反应速率与两个\mathrm{A}
粒子相互碰撞的可能性成正比，那么所研究反应的基本速率定律可以表示为：

式中，k_1称为反应速率常数（我们将在下文中对“常数”一词的使用进行限定，但此处可以假设它为常数。这也称为反应物\mathrm{A}中的“二阶”反应，因为反应速率与反应物浓度的二次方成正比：这一比例来自上述的碰撞论证。必须强调的是，质量作用定律并不适用于所有的化学反应；如上所述，观察到的速率定律与反应的实际机理并不直接相关。

在任何速率定律中，速率常数k的单位取决于反应阶次：在这种情况下，k_1的单位为(L/mol)/s（读作 “每秒每摩尔”）。我们现在可以用r_1表达式来确定\mathrm{A}和\mathrm{B}的浓度变化：

请注意\mathrm{A}和\mathrm{B}在各自方程式中的乘数-2和+1。这是由于产生一个粒子\mathrm{B}，需要消耗两个粒子\mathrm{A}。这些乘数被称为化学计量系数或化学计量数，通常用希腊字母nu(\nu) 表示。

化学速率定律产生了一组两个常微分方程（ODEs），实际上它比 COMSOL Multiphysics 用户遇到的通常与空间相关的偏微分方程（PDEs）更容易求解。上述反应系统的方程组可以很容易地被集成到以下方程中：

式中，c_\mathrm{A,0}代表反应容器中物质\mathrm{A}的初始浓度。下图显示了这个表达式与浓度的数值推导结果：

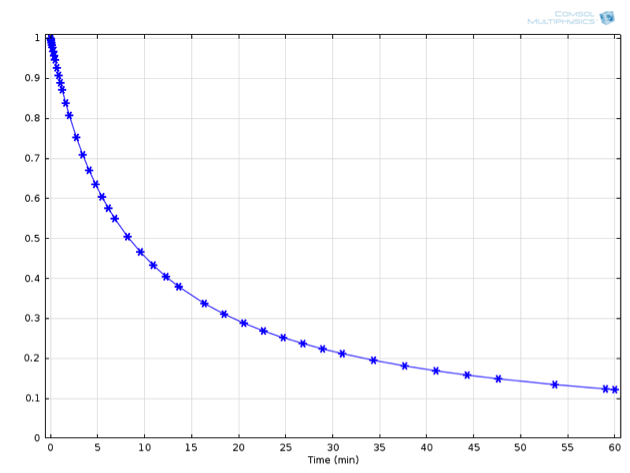
A 的浓度随时间的变化：数值解（星号）和解析解（实线）。

在这个例子中，\mathrm{A}的初始浓度为 1 mol/L，在 20°C 时，{k_1}的值为 0.001(L/mol)/s。

化学反应中的困难

一般来说，化学速率表达式是几个乘项的组合，对于包含j个化学物质的反应阶次为\nu_{ij}的反应i，用以下形式表示：

同样，反应阶次通常与化学计量系数对应，但对某些反应机理来说，情况并不一定如此。

很明显，这些表达式可以很快产生无法解析的方程组。这是一个特别重要的考虑，因为几个高度相关的化学系统（如燃烧、长链烃的裂解、生化系统等）可能涉及几十个甚至几百个参与物质，每种物质都有其对应的速率方程。但是，自从有了化学反应工程模拟，这里只需要添加一个额外的反应，就能够极大地简化计算量。回到我们感兴趣的系统，假设增值产品\mathrm{B}可以进一步反应成废料\mathrm{C}。所以：

这种串联反应并不只是学术上感兴趣的研究，实际上也是工业中最常遇到的化学体系之一。以工业化学中最大的一个领域——氧化反应为例，一个特定的挑战是将基体大程度地氧化，而非进行到基本没有价值的完全氧化物（在有机化学中，这可能是二氧化碳）。

新的反应速率可以写成：

和常微分方程：

请注意，物质 B 的表达式现在有两个反应项，因为它参与了两个反应。

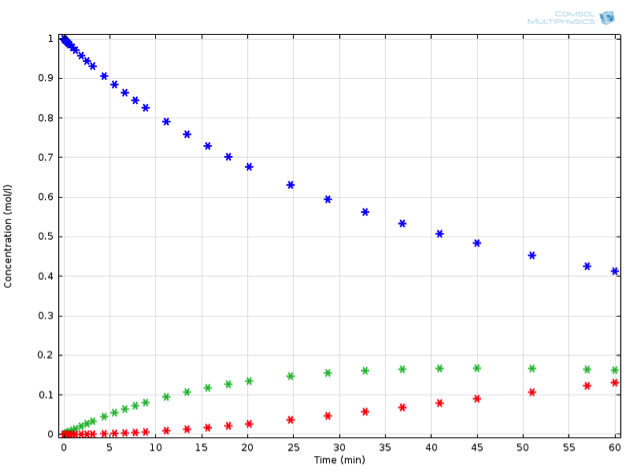
仅在系统中添加这样一个额外的反应，就使得常微分方程组的手动求解更难了。有数学头脑的读者可能有兴趣手动尝试一下——这个系统的浓度可以用一些不太熟悉的特殊函数以封闭形式表示。不过，使用化学反应工程模块来解决这个问题肯定要快得多，也更容易扩展。使用 COMSOL Multiphysics 求解这些方程，我们观察到下图中描述的行为（对于{k_2}，给定的测量值为 0.0015 1/s）。如果我们是设计这个反应过程的化学工程师，可能还需要有一些必须满足的非常具体的标准。

也许\mathrm{C}是一种有毒物质，其浓度可能不超过一个临界值。或者，除非超过\mathrm{B}产量的特定阈值，否则该过程在经济上是不可行的。假设是后面一种情况，在反应结束时，任何高于 0.15 mol/L 的\mathrm{B}的值都是可以接受的。

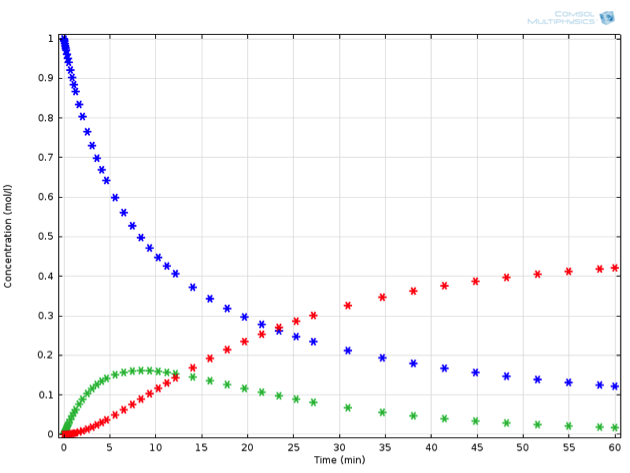
串联反应的例子：A（蓝色）转化为 B （绿色），B 又可以进一步反应为 C（红色）。

调整系统

如果我们的目标是由特定数量的\mathrm{A}获得一定数量的\mathrm{B}，就必须在大约 7 分钟后以某种方式停止或淬灭反应。由于这通常是不可行的，我们必须开始寻找其他方法来优化\mathrm{B}的产量。

让我们仔细看看反应速率“常数”的概念k。事实证明，两个\mathrm{A}粒子相遇并不足以发生反应，它们还必须以足够的能量相互撞击，来跨越一个不稳定的反应障碍（称为过渡态），转化为稳定的反应物状态。这个需要克服的能量被称为活化能。由于我们同时观察这么多的粒子（1 摩尔包含超过 10²³个分子），可以使用统计学来考虑，一定比例的粒子将以高于活化能的能量碰撞，而一定比例的能量则以低于活化能的能量碰撞。基于统计热力学和麦克斯韦-玻尔兹曼分布的概念，可以得出以下关于{k}的温度依赖性的方程：

这个方程被称为阿伦尼乌斯方程。

A(T)是所谓的指数前因子，或简称指前因子，通常被认为与温度无关。{E_A}是活化能，R是理想气体常数（=8.314 J/（K*mol））。回到我们选择的系统，假设通过简单的文献检索获得了反应 1 和反应 2 的必要参数。

将所有这些参数输入 COMSOL Multiphysics，就可以对反应温度进行优化，以获得进行该反应的理想温度。事实证明，只需将反应温度降低到 10°C，就能达到预期的标准：

在 10℃ 下进行的同样的串联反应。

结论和后续操作

COMSOL 软件对这个问题的定义既简单又直观。首先，反应可以直接输入，用 “=>” 代替 → 符号。之后，COMSOL Multiphysics 提供了输入阿伦尼乌斯参数和初始浓度的选项（在这个示例中，开始时只存在物质\mathrm{A}）。集成时间的选择在很大程度上取决于人们想要研究的动力学；化学反应可以发生在微秒到年的任何时间尺度上。之后，只需点击“计算”并选择输出格式，就能为你感兴趣的应用提供最多信息。

使用COMSOL 仿真软件，你可以研究即使是最简单的反应系统的复杂过程，在设计工业规模的反应过程时，COMSOL 可以为你提供宝贵的反馈。这个化学动力学系列博客的下一篇文章将探讨：当我们不能再应用简单的幂律方法来定义化学反应速率时会发生什么？以及这对你的下一顿牛排晚餐可能意味着什么？

系列博客的其他文章

1. 酶动力学，米氏动力学
2. 使用 COMSOL Multiphysics 估算化学参数
3. 氨的合成，一个复杂的非线性过程