
在本篇博客文章中,我们将和大家一起探讨测试电磁分析方法(Testing Electromagnetic Analysis Methods,简称 TEAM)研讨会问题 30a中描述的三相感应电机问题。我们使用了旋转机械,磁接口中的瞬态求解器对二维感应电机进行分析,然后通过将电磁场分析与包含惯性效应在内的转子动力学相耦合,进而研究了电机启动时的动力学问题。在文章的末尾,我们还将标准模型的结果与用 COMSOL Multiphysics 得到的仿真结果进行了对比。
借助仿真创建感应电机模型
三相感应电机由固定部分和旋转部分组成,固定部分称为定子,包括叠压钢片和三相线圈;旋转部分称为转子,包括导电铝条和转子钢。如下图所示,定子中暴露在外的三相绕组分别被标记为 A、B 和 C,三个绕组彼此之间的相位差为 120°。每个绕组的相位都跨越 45°,并由中间的空气隙隔开,且定子的外直径为 5.7 cm。
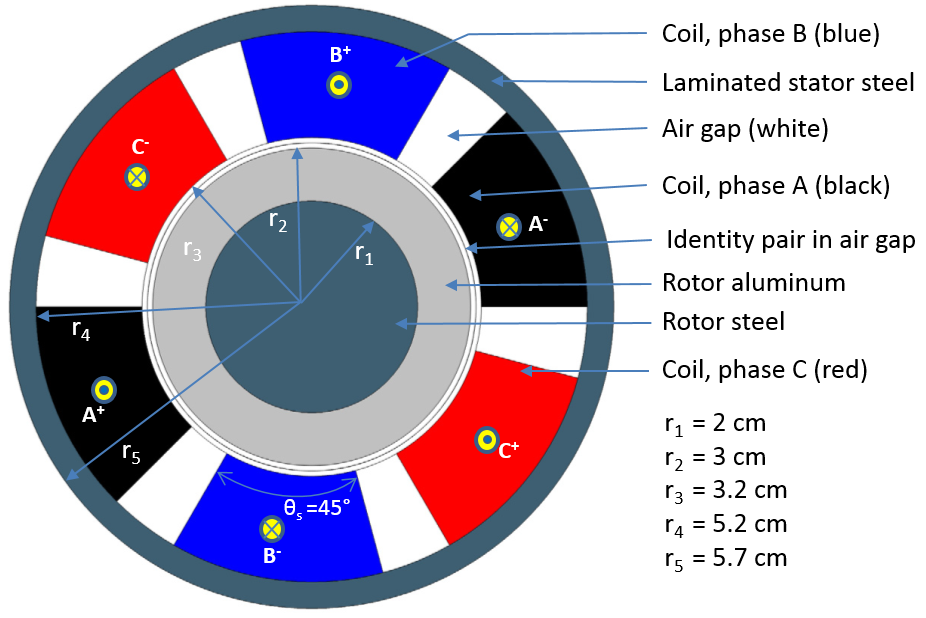
图像描绘了三相感应电机结构的尺寸和相位布局。
电机的电流密度维持在 310 A/cm2,这等同于每个绕组上的 RMS(均方根) 电流Irms= 2045.175。三相绕组的激励频率为 60 Hz。转子钢和定子钢片的恒定相对磁导率μr= 30。定子由钢片叠压而成,其电导率σ= 0;转子钢的电导率σ= 1.6e6 S/m。同样地,转子铝条的电导率σ= 3.72e7 S/m。
在 COMSOL Multiphysics 中模拟感应电机的动力学
当在 COMSOL Multiphysics 中创建感应电机的几何模型时,我们创建了两个并集,分别用于定子域和转子域。之后我们通过执行“形成装配”操作来完成感应电机的几何创建,进而可以在转子和定子之间自动创建一致对,此视频对这一操作进行了详细阐释。
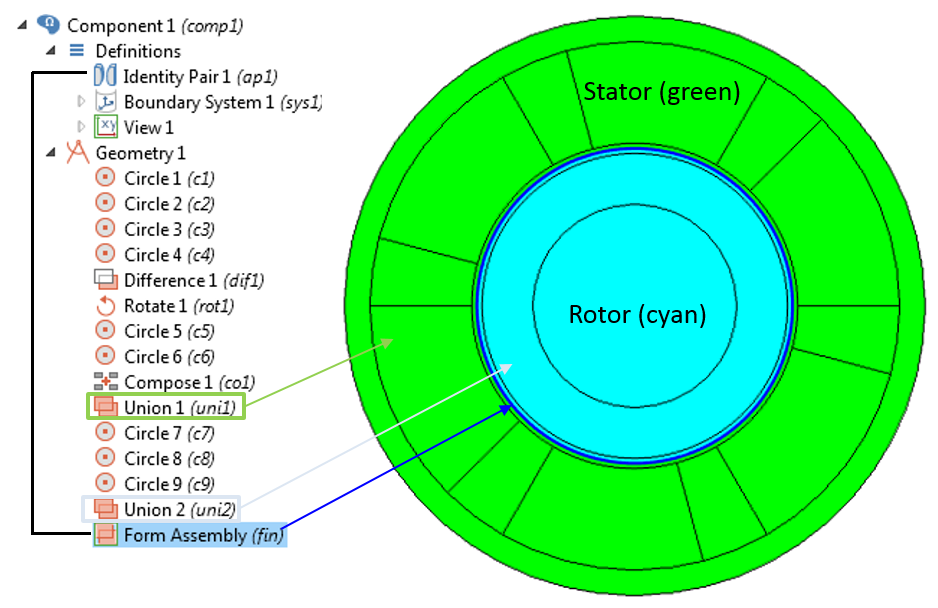
感应电机的几何序列。通过在转子和定子这两个并集之间使用 “形成装配 ”来完成几何创建。
下表列出了该模型中使用的材料属性。测试电磁分析方法的原始文件并未规定材料密度,因此,我们假设转子钢和铝条的密度分别为 7850 kg/m3 和 2700 kg/m3,并分别计算了转子的转动惯量。
| 材料 | 电导率(σ) | 相对磁导率(μr) | 密度(ρ) |
|---|---|---|---|
| 转子钢 | 1.6e6 [S/m] | 30 | 7850 [kg/m^3] |
| 定子钢 | 0 [S/m] | 30 | 非必要条件 |
| 转子铝条 | 3.72e7 [S/m] | 1 | 2700 [kg/m^3] |
| 空气 | 0 [S/m] | 1 | 非必要条件 |
我们使用旋转机械,磁接口来模拟这个三相感应电机中的电磁场。由于所有的电磁材料属性均为线性,所以无需对默认的安培定律节点做任何修改。
我们使用了均匀和多匝线圈特征来模拟三相。每个绕组的匝数n0 = 2045。每匝导线都带有1[A]的电流,同时三相之间的相位差为 120°。流经三相的电流可描述为:
IA= 1[A]*cos(w0*t)*sqrt(2)IB= 1[A]*cos(w0*t+120[deg])*sqrt(2)IC= 1[A]*cos(w0*t-120[deg])*sqrt(2)
这里,1[A]为输入电流的 RMS 值,因此我们需要将它与sqrt(2)相乘以获取峰值。
使用旋转机械,磁接口中的计算力特征可直接获取转子中的电磁扭矩。添加了该特征后,我们在后处理时即可获取该接口中磁力的空间分量(rmm.Forcex_0,rmm.Forcey_0,rmm.Forcez_0)以及轴向扭矩(rmm.Tax_0)。“计算力”特征只对域选择的整个外边界上的 Maxwell 应力进行积分。由于这种方法基于表面积分,因此计算力很容易受到网格大小的影响。使用这种方法时,往往需要执行网格细化研究,才能正确地计算力或扭矩。
另一种方式是使用 Arkkio 方法计算扭矩,即求解磁通密度的体积分。在该方法中,二维旋转电机模型的电磁扭矩可通过下方表达式进行计算:
其中,r_o为外半径,r_i为内半径,S_{ag}为气隙的横截面积。径向和方位角方向上的磁通密度分别为B_r和B_\phi。参考以下屏幕截图,了解更多关于在 COMSOL Multiphysics 中执行 Arkkio 方法的详细信息。
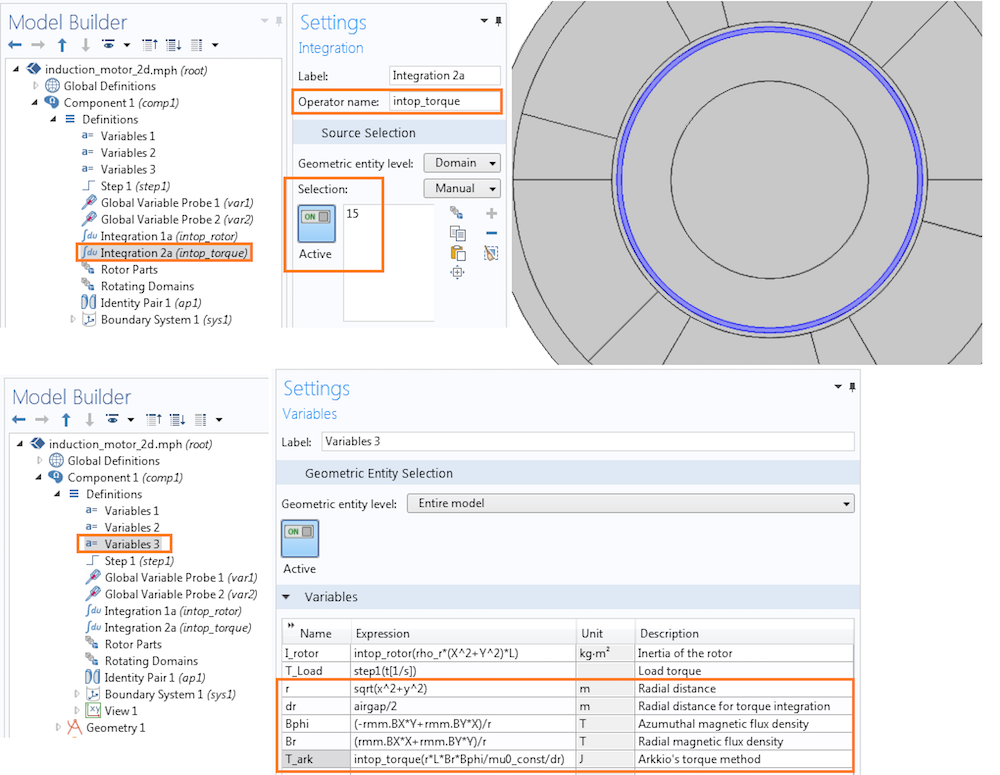
利用 Arkkio 方法计算得出的感应电机的扭矩。
使用全局常微分和微分代数方程接口模拟电机的动力学
转子的旋转运动遵循以下两个方程:
(1)
(2)
其中,T_m为转子的轴向电磁扭矩,T_L为负载扭矩,\omega_m为转子的角速度,\phi为转子的角位置。
通过在如下图所示的两个独立的全局方程节点内使用全局常微分和微分代数方程接口,我们成功地模拟了转子的旋转运动。
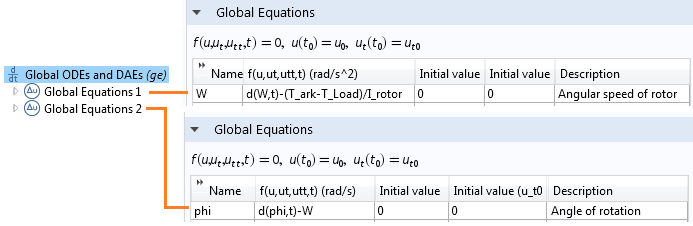
使用全局常微分和微分代数方程接口执行转子角速度和旋转角的微分方程。
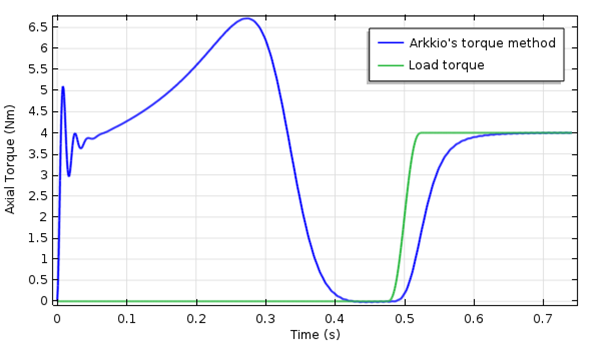
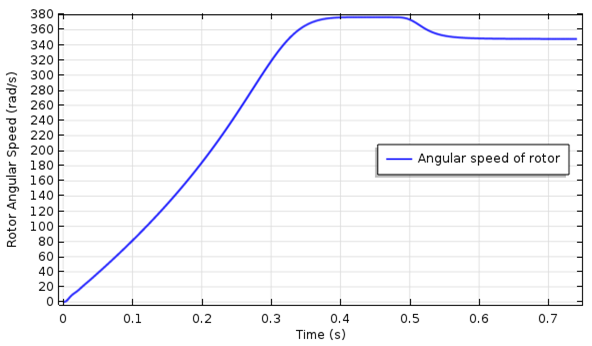
转子瞬态电磁扭矩与时间的关系(左图),以及转子角速度与时间的关系(右图)。
电磁扭矩在启动过程中会表现出振荡行为,并在 0.28 秒左右逐渐达到最高值。当在 0.4 秒左右时,转速完全同步,此时扭矩会降为 0。然后在 0.5 秒时,对其应用一个阶跃变化的负载扭矩,感应电机便会通过降低速度来逐渐产生等量的扭矩。
COMSOL Multiphysics 与 TEAM 问题 30a 的结果对比
为了将电磁扭矩、感应电压及转子损耗与 TEAM 问题 30a 的结果进行比较,我们使用磁场物理场接口在频域内建立了相同的感应电机模型。该模型通过添加用于描述速度的洛伦兹项,从而引入了旋转运动。您可以点击此链接下载三相感应电机的模型案例。
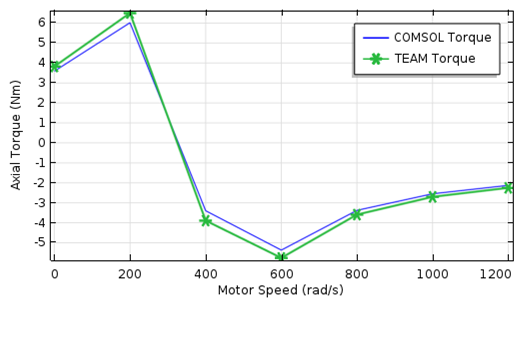
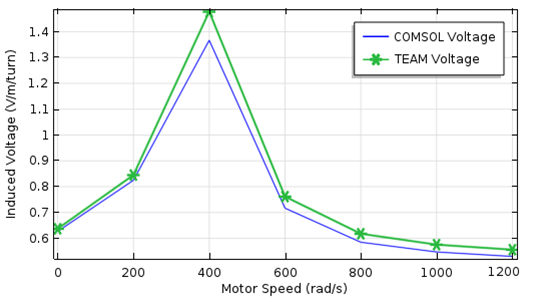
图像将轴向扭矩与电机转速的关系(左图)和感应电压与电机转速的关系(右图)进行了对比。
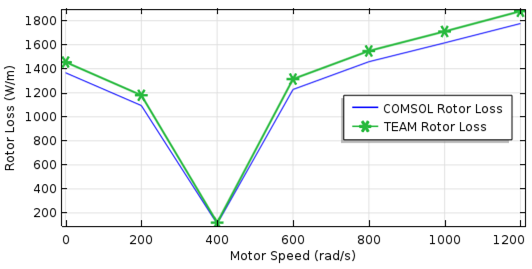
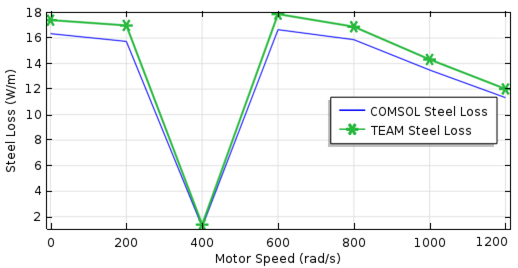
图像将转子损耗与电机转速的关系(左图)和转子钢损耗与电机转速的关系(右图)进行了对比。
更多关于使用 COMSOL Multiphysics 模拟感应电机的资源
- 参考以下教学模型,尝试模拟感应电机:
- 阅读以下博客文章,了解更多关于旋转机械建模的信息:
- 阅读电磁设备系列的更多博客文章



评论 (0)