涡轮分子泵是一种能够达到超高真空(UHV)条件的机械真空泵。由于气体分子之间相互碰撞概率较低,所以需要专用的数值方法模拟超低压条件下的气流。COMSOL Multiphysics®软件提供了两种完全不同的计算方法用于模拟高度稀薄气体:角系数方法(angular coefficient method)和蒙特卡罗方法(Monte Carlo method)。在这篇博客文章中,我们介绍了如何使用蒙特卡罗方法对涡轮分子泵进行模拟。
编者注:此文最初发布于 2017 年 8 月 9 日。现已更新以反映软件的最新功能。
真空系统简介
在许多高科技工业应用(例如半导体芯片的制造)中,我们都能发现真空技术。真空环境在基础研究中也是必不可少的。例如,粒子加速器无法在正常大气压下工作,因为被加速的粒子大概率会与周围的空气分子发生碰撞。

典型的真空腔室。
在真空环境中,气体的绝对压力远低于典型的海平面大气压,后者约为 101,325 帕斯卡(Pa)或 14.7 磅每平方英寸(psi)。大气主要由氮气和氧气组成,但是在处理真空室时,必须考虑包含的每种气体,甚至腔室壁及配件的排出气体,润滑剂(升华和蒸发气体)也会对真空室压力产生重大影响。
真空泵用于抽除真空室中的气体,从而降低真空室内压力。真空泵有许多不同的类型,包括:
- 旋片泵
- 定片泵
- 扩散泵
- 涡轮分子泵
- 低温泵
- 离子泵
通过串联的方式使用两种或多种不同类型的泵非常普遍,每种泵都有其适合的特定压力范围。例如,旋片泵或定片泵可以在大气压下排出空气,同时将真空室的压力降低到小于 0.1Pa 左右。涡轮分子泵可以达到超高真空条件(小于 10-7Pa),但在大气压下却无法正常工作。为了将压力从大气压一直降低到超高真空,我们首先可以使用旋片泵(以这种方式使用时被称为粗抽泵)将压力降至 0.1 Pa,然后使用涡轮分子泵将压力从 0.1Pa 降低至 10-7Pa。

涡轮分子泵。
但要注意的是,在实际工作中真空泵并不能达到理想的真空度。在大气压和室温下,1 立方米的空气中有超过 1025个分子。即使在超高真空中,1 立方米的空气中仍包含数万亿个分子!我们抽真空目的不是要排除所有的空气分子,而是要尽量排除足够多的空气分子,以免它们阻碍腔室内的实验或制造过程。
真空系统中的稀薄气流
涡轮分子泵只有在通过其的气流是自由分子流时才能工作。换句话说,气体压力必须足够低,以使分子撞击周围表面的频率比分子间的碰撞的频率更加频繁。因此,该泵仅在使用粗抽泵将压力降低到约 0.1Pa 之后才能实现超真空条件。
通常,在考虑气流时,我们会将气流设想为连续流。当空气通过狭窄的通道流入房间时,这股空气会散开,并可能在所有侧面形成再循环区域。当流动的空气到达障碍物时,我们期望它能绕开障碍物流动,填充其后面的空间。由于空气中的氮、氧和其他气体分子每秒会相互碰撞数十亿次,因此它会以这种方式运动。
在极低的气压下,气体表现为自由分子流,气体流动主要由分子-壁碰撞而不是分子-分子碰撞控制。如果气体从狭窄的孔口释放到大的开放空间中,那么大多数分子将不会因分子间碰撞而向四面八方扩散,而是会沿几乎同一个方向飞出,这种现象被称为分子束射。
当气体分子撞击表面时,它们可能会被表面吸附或反射离开表面。即使表面肉眼上看起来非常光滑,分子也会在表面在随机方向上反射分子。一个合理的近似是给以不同反射角的概率分布。通常,此概率分布函数在垂直于表面的方向上对称。
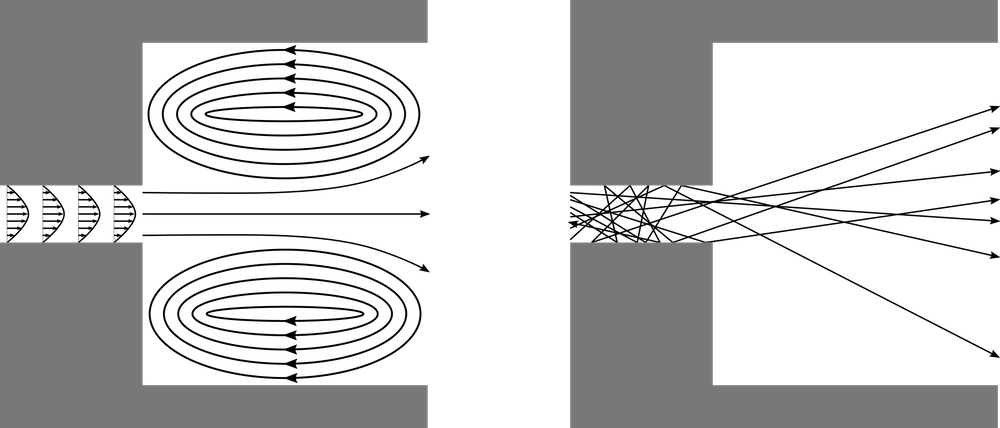
通过窄管进入腔室的连续流(左)和分子流(右)的比较。
涡轮分子泵详解
设想一下,如果用平板或球拍击打球,那么在球与球拍接触时会朝不同的方向弹跳,具体取决于球拍的角度。这就是涡轮分子泵的基本工作原理。
涡轮分子泵由许多环组成,这些环相互堆叠,并沿一条公共轴线排列。其中一些环绕轴旋转,称为转子,其他的环被固定在一个固定的位置上,称为定子。一个典型的设计可能包含多对交替的转子和定子。每个环内有许多狭窄的倾斜叶片。通常,环中的每个叶片以相同的角度倾斜并且等距分布。因此,如果有N个叶片,那么环具有N倍轴向对称性。
由于叶片在转子中倾斜,当分子撞击叶片时,它更有可能沿一个方向从转子弹回,而不是朝相反方向弹出。下面的图示即显示了一个没有相邻定子的单个转子中的这种运动行为。假设此叶片环逆时针旋转,如红色箭头所示。一个分子更有可能击中这些叶片之一的底面而不是顶面。这些分子更可能向下偏转(沿蓝色箭头的方向)而不是反向弹出。分子这种向下方向的优先偏转,可以减小在该转子上方区域中的气压。
为了使传输概率的差异(从上到下与从下到上)更大,叶片表面的移动速度应等于或大于分子的平均热速度。对于室温下的大多数气体,该速度约为每秒几百米,但是对于非常轻的气体(如氢气),速度明显更高。因此,当使用涡轮分子泵将腔室压力降低至超真空时,腔室中的大多数残留气体将为氢气(参考文献1)。
涡轮分子泵的叶片由被称为级的单元组成。典型的泵级可能包含8–20个这类在转子和定子之间交替的叶片环(参考文献2)。为简单起见,我们当前的模型仅考虑了单个转子。
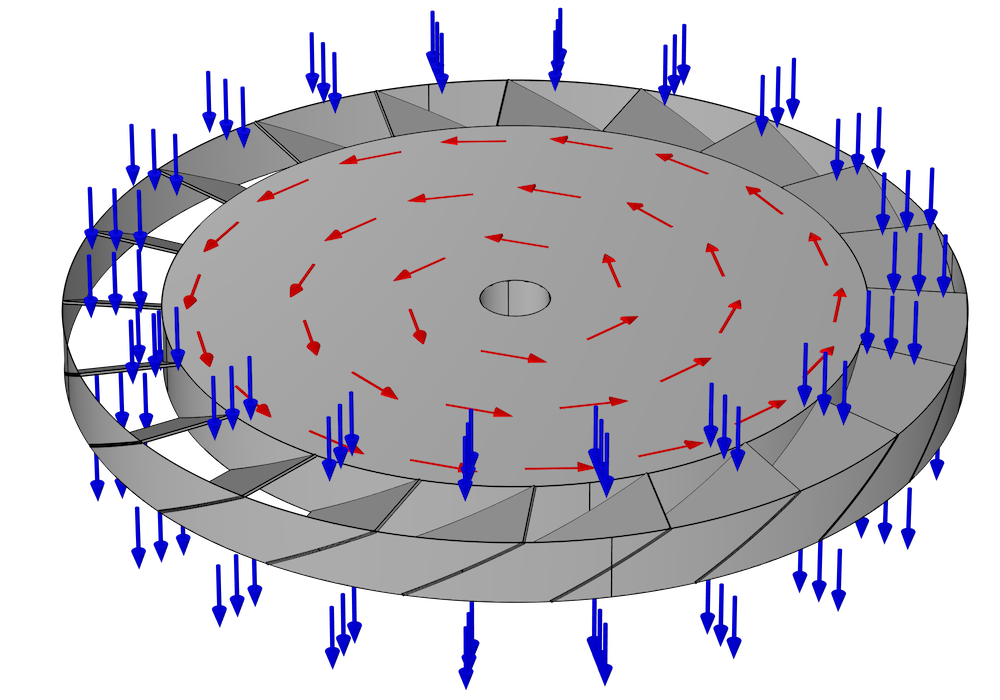
通常,我们建立涡轮分子泵数值模型的主要目的是预测其泵速和压力比。这些参数可以通过分子在整个叶片环上的传输概率来预测,即从顶部进入级后从底部离开的分子比率,反之亦然。
选择数值方法
在 COMSOL® 软件中,有 2 种主要的数值方法可用于模拟极稀薄气流。一种称为角度系数法,可以通过分子流模块提供的自由分子流物理场接口使用。角度系数方法是一种视图因子计算,可以计算模型边界处的分子通量,并假设气体分子只会与壁碰撞而不会与其他分子碰撞。角系数方法的主要缺点是它是准静态的,也就是说,它忽略了分子的有限飞行时间。在这里,这是一个重要的因素,因为与分子速度相比,叶片很容易达到每秒数百米的速度。
为了充分计算叶片在涡轮分子泵的运动,我们将选择使用粒子跟踪模块下的数学粒子追踪接口执行蒙特卡罗方法进行模拟。在蒙特卡罗模型中,我们通过求解牛顿运动定律来解决气体中单个分子的运动。由于计算成本的限制,泵中单个分子的实际数量可能太大,因此无法单独对每个分子进行建模,但是我们可以采用一个有代表性的分子群样本(例如 100,000 个)进行建模,然后对整个分子群进行推算。
用蒙特卡罗法预测气体分子在简化的涡轮分子泵级中的传输概率,该级由单个旋转叶片环组成。正如我们前面所讨论的,包含N个叶片的典型泵转子通常会表现出N倍旋转对称性。因此,我们仅考虑通过两个相邻叶片之间的单个间隙的分子,便可以进一步简化模型并降低计算成本。
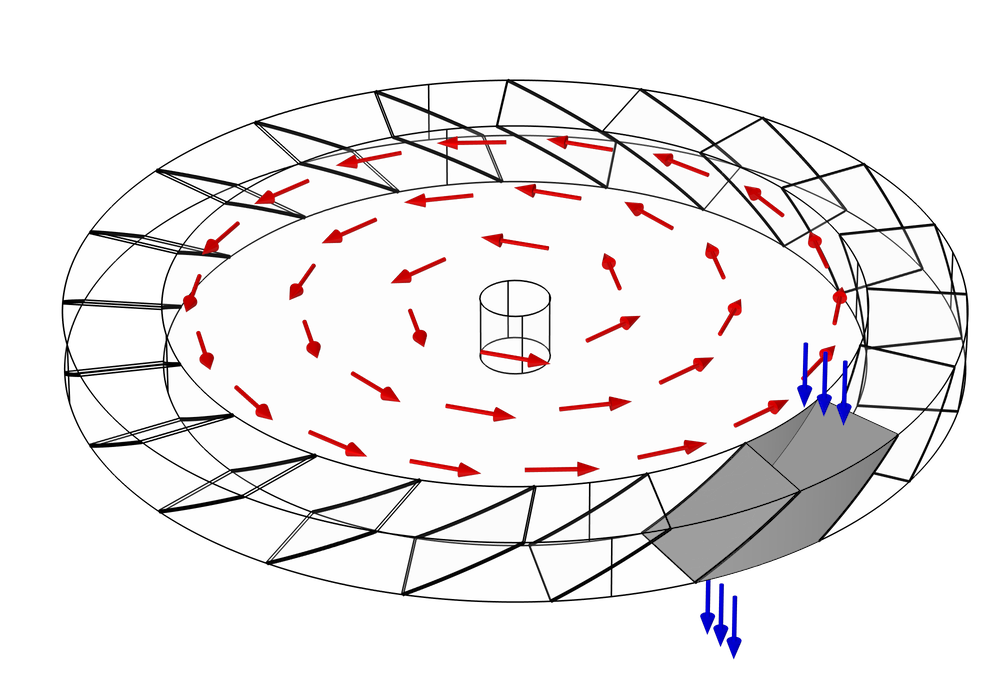
叶片之间的间隙也由两个圆柱形表面(内部的根壁和外部的顶壁)界定。我们可能会从前面的 2 个图看到,分子可以穿过的实际空间不是整个圆盘,而是一个距离旋转轴有一定距离的环形区域。这是因为叶片上任一点的速度与其从中心到径向的距离成正比,
因此,无论转子旋转多快,尝试将根壁移到更靠近旋转轴的方向上,收益都会减少。
角速度的实际限值是每分钟小于 100,000 转(参考资料1)。
选择参照系
在选择参照系时,我们的模拟域是前后由相邻叶片界定,而在左边和右边则由根壁和顶壁界定的空白区域。气体分子可能会从顶部和底部进入域,我们的目标是确定从顶部释放的分子中有多少会从底部出来,反之亦然。
在这里,我们遇到了另一个技术挑战:转子叶片之间的空间沿圆周运动。在移动域中进行建模时,必须决定在模型中使用哪个参照系。通常,选择下列选项之一:
- 在“实验室”参考系中建立模型。也就是说,从观察者站在静止不动的外部并观察其旋转的角度对转子进行建模。为此,我们可能必须使用专用的旋转域节点显式地使几何图形随时间旋转。从这个角度来看,分子从一个表面移动到另一个表面时遵循直线路径。
- 在连接到转子的可移动参考系中建立模型。就是说,想象一下,如果观察者能够缩小并乘坐上这些转子叶片之一,分子的轨迹将如何?在此参考系中,单个气体分子遵循的路径可能看起来是弯曲的。
在此示例中,我们将使用第二种方法建模。但是,这带来了额外的复杂性,下面我们将详细介绍。
旋转参照系中的粒子追踪
这些分子遵循牛顿第二运动定律,
其中,q是粒子位置,mp是粒子质量,Ft是所有作用力的总和。
在这个示例中,我们忽略了重力,因此合力为零。但是牛顿第二定律是在惯性参考系中制定的,这意味着它只有在观察者不加速时才成立。旋转是一种加速度,因此该模型是在非惯性参考系中建立的。
为便于理解惯性和非惯性参考系,请想象一下在移动的卡车后面尝试执行简单的物理实验(例如,弹跳球或跟踪摆的运动)。如果卡车停止或在巡航控制系统打开的情况下以直线行驶,则这些实验将得到相同的结果。但是,如果卡车加速,减速或转弯,实验将得出不同的结果。
如果从根壁到顶壁的距离比从旋转轴到根壁的距离小得多,也就是说,
那么,作为第一近似,我们可能会忽略我们的参考系非惯性这一事实。
实际上这等效于将叶片环视为一条无限直线的叶片,它们都沿相同方向移动。这个准 2D 涡轮分子泵教程模型中做了这样的假设,并在参考文献3进一步讨论。这种简化的假设大大减少了所涉及的计算工作量,因为它使粒子在连接到叶片的参考系中沿直线移动。当转子缓慢旋转时,这是一个合理的近似,但是随着转子角速度的增加,它的准确性将降低。
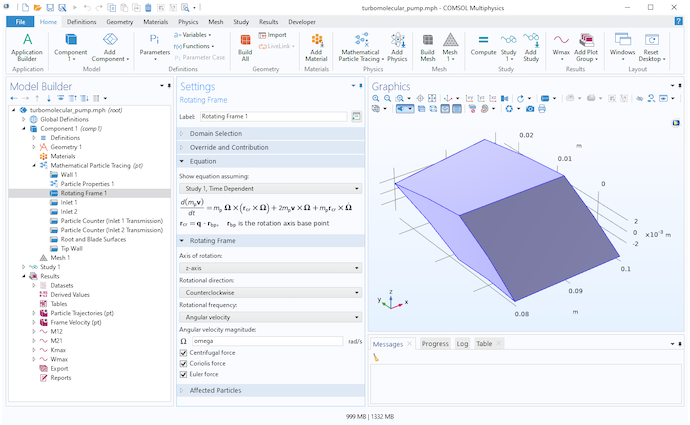
为了执行高保真的蒙特卡罗模拟,必须考虑我们的参照系在旋转这一事实。幸运的是,“数学粒子追踪” 接口提供了专门用于此目的的专用物理功能。我们可以将旋转域节点添加到模型中,用于定义在旋转参照系中追踪粒子而产生的虚拟力,
\mathbf{F}_\textrm{t} &= \mathbf{F}_\textrm{cen} + \mathbf{F}_\textrm{cor}\\
\mathbf{F}_\textrm{cen} &= m_\textrm{p}\mathbf{\Omega}\times\left(\mathbf{q}\times\mathbf{\Omega}\right)\\
\mathbf{F}_\textrm{cor} &= 2m_\textrm{p}\mathbf{v}\times\Omega
\end{align}
这些虚拟的力称为离心力Fcen和科里奥利力Fcor。在这些等式中,v是粒子速度,Ω是旋转参考系的角速度。为简单起见,这里假设旋转轴穿过原点。
粒子释放和边界条件
通过将旋转域节点添加到模型,将自动定义离心力和科里奥利力。剩下的就是定义粒子释放和边界条件。
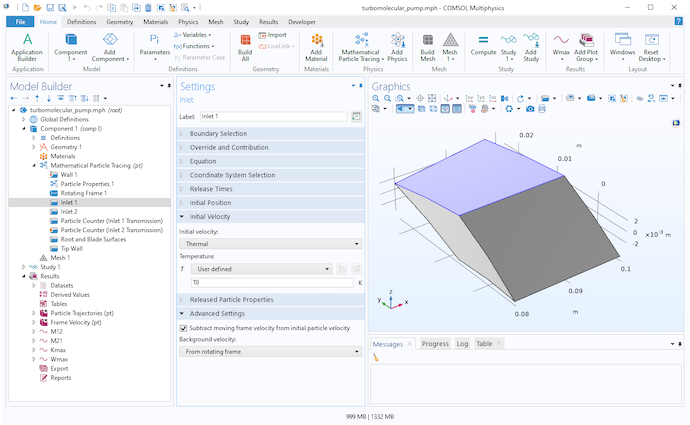
使用顶部和底部边界上的入口节点将分子释放到模拟域中。该模型使用热速度分布,其中每个分子的初始速度从麦克斯韦分布中采样,并根据余弦定律采样其初始方向。
然后,从释放的分子速度中减去叶片速度,因为在实验室参考系中,与泵级相邻的区域中的气体漂移速度为零。
叶片壁、根壁和顶壁均使用热再发射边界条件。每当分子撞击到这些表面之一时,就会以新的随机速度和随机方向弹回到区域中。假定叶片壁和根壁与旋转参考系一起移动,而顶壁则假定固定在实验室(惯性)参考系中。对于击中顶壁的任何分子,使用内置设置从重新初始化的粒子速度中减去运动参考系的速度。
结果
传输概率定义是释放的分子将从泵级的一侧穿过到另一侧,而不是被叶片弹回的比例。当叶片旋转时,我们可以定义两个不同的传输概率:正向(在上图中,从上到下)和反向(从下到上)的传输概率。
根据分子在向前和向后的传输概率,我们可以获得最大压缩比Kmax和最大速度因子Wmax,
其中,M12是正向的传输概率,M21是反向的传输概率。
下面,让我们看一些将这些传输概率与无量纲速度比C进行比较的图。这是叶片速度(以均方根或均方根半径测量)与气体中分子最可能的速度之比。分子速度是分子质量和气体温度的函数。通常,分子在较热的气体中运动更快,而较轻的分子则比较重的分子运动更快。因此,涡轮分子泵在抽出氩、氮和氧等较重的物质方面表现更好,但在抽氢方面效率较低(参考文献2)。
当叶片静止时(C = 0),向前和向后的传输概率大致相等。随着叶片开始更快地旋转,正向的概率接近 1,而反向的概率接近零。
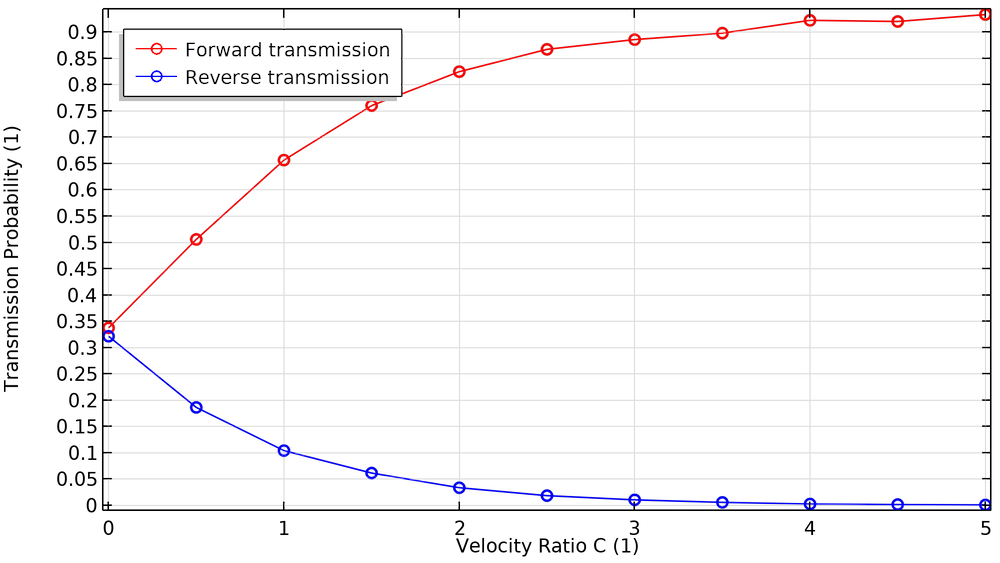
正向和反向传输概率随速度比的变化。
我们还研究了叶片的速度比如何影响压缩比和泵速。为了产生足够的压缩和速度,分子泵使用了由多个圆盘和不同类型的叶片组成的多个叶片结构。靠近腔室入口的叶片设计为具有较高的泵送速度和较低的压缩比,而靠近前级真空管线(与粗抽泵的连接部)被设计为具有较低的泵送速度和较高的压缩比。
当这些叶片的速度增加时,如下图所示,最大压缩比和速度因子增加。这些图与参考文献4中报道的类似研究非常吻合。
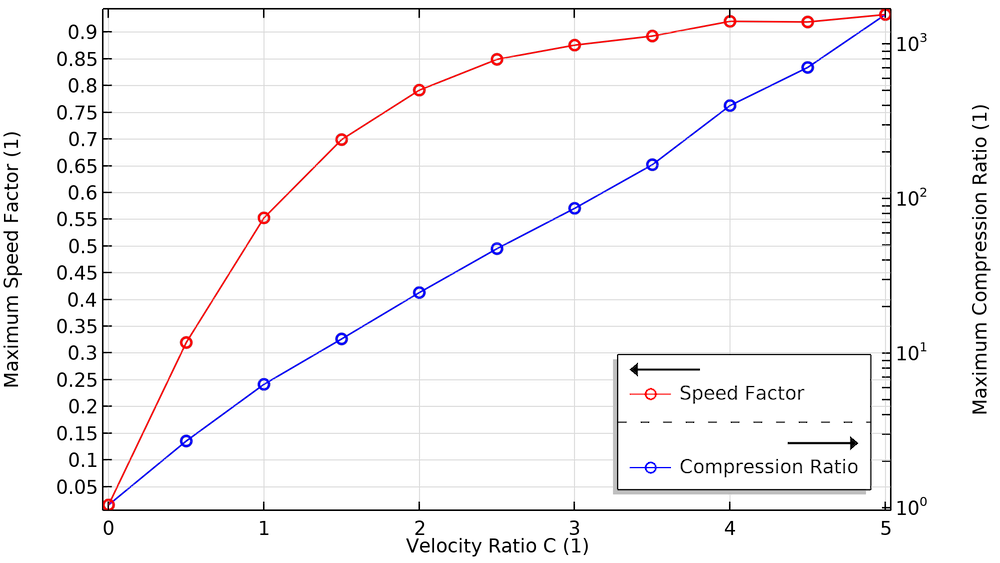
叶片速度对最大压缩比和最大速度系数的影响。
后续操作
这个示例重点介绍了几个功能,这些功能让我们更加便捷地使用蒙特卡罗方法模拟涡轮分子泵。单击下面的按钮,尝试自己建模。
了解有关 COMSOL Multiphysics®中粒子追踪的更多信息
请查看以下有关粒子追踪的博客文章:
参考资料
- J.M. Lafferty, ed.,Foundations of Vacuum Science and Technology, John Wiley & Sons, 1998.
- J.F. O’Hanlon,A User’s Guide to Vacuum Technology, 3rd ed., John Wiley & Sons, 2003.
- S. Katsimichas, A.J.H. Goddard, R. Lewington, and C.R.E. De Oliveira, “General geometry calculations of one-stage molecular flow transmission probabilities for turbomolecular pumps,”Journal of Vacuum Science & Technology A: Vacuum, Surfaces, and Films, vol. 13, no. 6, pp. 2954–2961, 1995.
- Y. Li, X. Chen, Y. Jia, M. Liu, and Z. Wang, “Numerical investigation of three turbomolecular pump models in the free molecular flow range,”Vacuum, vol. 101, pp. 337–344, 2014.



评论 (0)