
COMSOL Multiphysics® 软件中的电容计算很简单。如果你只有两个导体,最简单的方法是:将一个导体设为接地,另一个设为终端,然后求解。此时,内置变量会给出电容值。但是如果你有两个以上的导体,比如触摸屏、传输线和电容式传感器,怎么办呢?如果你对标准教科书术语感到困惑,请按照本博客中计算电容矩阵的工作示例进行操作。
什么是自电容?
电容是系统存储电荷的能力,通常可以定义为物体相对于接地参考电位升高 1 伏所需的电荷量。在线性系统中,表达式如下
其中 Q 是电荷,V 是对地电位差,C 是电容。
在我们讨论多导体系统之前,请记住,根据定义,即使是单个孤立导体也有电容,它是以相对于无限远的接地球壳定义的。对于导电球体,自电容是
例如,我们可以使用这个公式来计算地球的自电容——大约是 710 微法。
人体也可以带电。
因此,人体也表现出自电容(也称为人体电容)。根据姿势和周围区域的不同,人体电容在 100 皮法范围内,甚至会在人体内产生刺痛感。例如,早上梳头时,你可以轻松地将你的人体电容充电到几千伏。在开始新的一天之前,一定要精力充沛!
互电容矩阵和麦克斯韦电容矩阵的比较
在典型的电力系统中,多个导体之间的电容是最重要的。互电容(也称为寄生电容或杂散电容)是在两个电荷体之间产生的期望的或不期望的电容(电荷积累)。如果将一个带电物体放到另一个物体附近,第一个物体上的电荷分布将因静电感应过程而改变(不要与电磁感应混淆)。特别是在传输系统中,线路之间的电容耦合通常是非预期的,是比较棘手的问题,原因是它会产生噪声。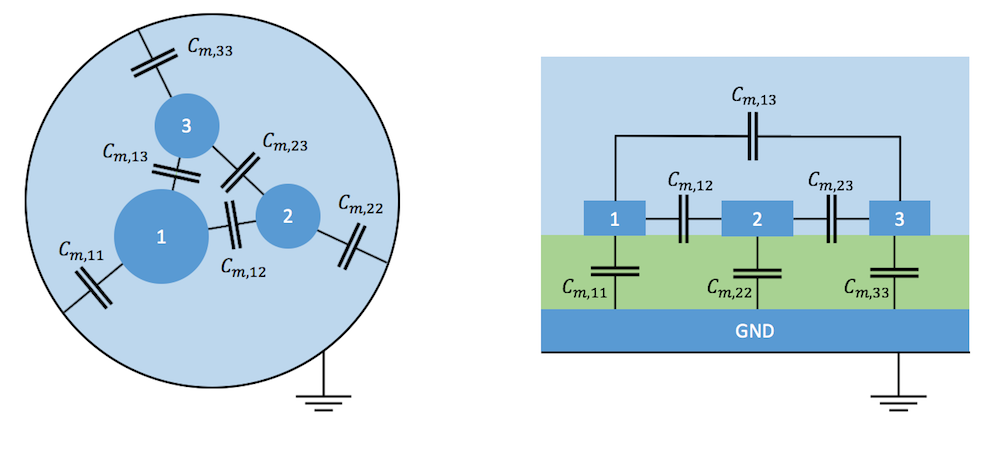 带屏蔽层三芯电缆(左)和接地板上微带传输线之间互电容(右)的典型示例。从连续场模型到具有分立电容器的集总模型的转变意味着将导体收缩为点,同时将导体表面的电荷移动到它们之间的电容器的极板上。
带屏蔽层三芯电缆(左)和接地板上微带传输线之间互电容(右)的典型示例。从连续场模型到具有分立电容器的集总模型的转变意味着将导体收缩为点,同时将导体表面的电荷移动到它们之间的电容器的极板上。
为方便起见,可以矩阵形式排列一个由 N 个导体和一个附加接地板组成的系统的互电容:
C_{m,21} & C_{m,22} & \dots & C_{m,2N} \\
\vdots & \vdots & \ddots & \vdots \\
C_{m,N1} & C_{m,N2} & \dots & C_{m,NN}\end{bmatrix}
当你将物理系统简化为离散元件网络时,该矩阵的系数(也称为部分电容或集总电容)用于电路仿真器。
在场论中,另一种矩阵形式更常见:麦克斯韦电容矩阵。因为名称非常相似但系数不相同,所以理解互电容矩阵与麦克斯韦电容矩阵之间的关系非常重要。麦克斯韦电容矩阵描述了第 i 个导体的电荷与系统中所有导体的电压之间的关系。
C_{21} & C_{22} & \dots & C_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
C_{N1} & C_{N2} & \dots & C_{NN}\end{bmatrix}\begin{pmatrix}V_1 \\
V_2 \\\vdots \\V_N\end{pmatrix}
当只有电位V_1=1和所有其他电极接地时,可以通过测量导体 1 上的电荷来确定麦克斯韦电容矩阵系数C_{11}。因此,该矩阵通常也被称为接地电容矩阵。它的倒数C^{-1}矩阵。
我们还可以通过对自电容和互电容的贡献求和来计算导体 1 上的总电荷,如下所示。
&= & (C_{m,11}+C_{m,12}+C_{m,13})V_1-C_{m,12}V_2-C_{m,13}V_3)\end{matrix}
对于具有 N 个导体的系统,互电容矩阵和麦克斯韦电容矩阵之间的关系如下
Q_2 \\\vdots \\Q_N\end{pmatrix} = \begin{bmatrix}\sum_{}{^N_{i=1}} C_{m,1i} & -C_{m,12} & \dots & -C_{m,1N}\\
-C_{m,21} & \sum_{}{^N_{i=1}} C_{m,2i} & \dots & -C_{m,2N}\\ \vdots & \vdots & \ddots & \vdots \\
-C_{m,N1} & -C_{m,N2} & \dots & \sum_{}{^N_{i=1}} C_{m,Ni}\end{bmatrix} \begin{pmatrix}V_1 \\
V_2 \\\vdots \\V_N\end{pmatrix}
你可以通过其负的非对角元素轻松分辨出麦克斯韦电容矩阵。
操作示例:两个球体的互电容
我们已经清楚地定义了术语,现在我们来探讨在 COMSOL Multiphysics 中计算任意导体系统的电容矩阵是多么简单。为了感受坚实的基础,我们将从一个具有已知解析解的系统开始。(我说过我喜欢解析解吗?实际上,每当我开始一个新的仿真项目时,我都会尝试找到一个带解析解的简单系统来重现。)
在我们的例子中,我们可以使用一个由半径分别为a和b的两个导电球体组成的系统,这两个球体相距为c,无限远处接地。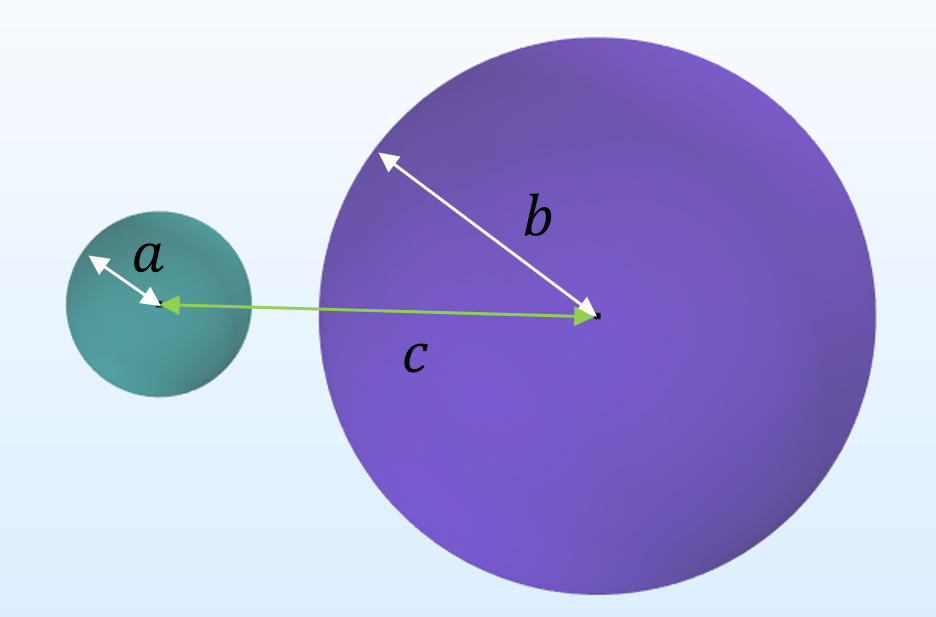 自麦克斯韦时代以来,这种系统的闭合表达式就已为人所知。我指的是 de Queiroz(2003)和 Lekner(2011)的两本现成出版物。三个麦克斯韦电容矩阵的表达式如下
自麦克斯韦时代以来,这种系统的闭合表达式就已为人所知。我指的是 de Queiroz(2003)和 Lekner(2011)的两本现成出版物。三个麦克斯韦电容矩阵的表达式如下
其中
{2ab}
\quad and \quad F=4\pi\epsilon_0 \cdot 1[m]
你可以在 COMSOL Multiphysics 中使用求和运算符轻松地将这些表达式声明为变量:
通过对 N 运行参数化扫描,我们发现当球体彼此不太靠近时,这些级数会迅速收敛。对于给定的如下一组参数,我们可以放心地将 N 设置为 10:a = 0.1,b = 0.3,c = 0.5。
为了计算“静电”接口中的电容矩阵,我们将一个终端条件设置为一个电位为 1 V 的球体。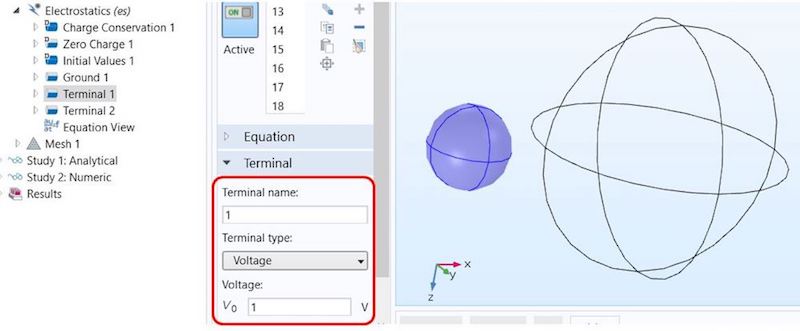
接下来,我们复制该特征,将其应用于第二个球体,并将终端名称设置为 2。为了计算电容矩阵,我们需要对终端应用不同的电压或电荷模式。出于教学原因,我们将讨论传统的手动终端扫描,然后介绍 COMSOL® 软件 5.3 版本中发布的速度更快的新技术。虽然新技术在一大类非常常见的问题中速度更快,但手工方法更普遍。
手动终端扫描直接在静电接口中激活。
在全局参数部分中声明扫描参数名称(默认为PortName)后,可以对PortName运行参数化扫描。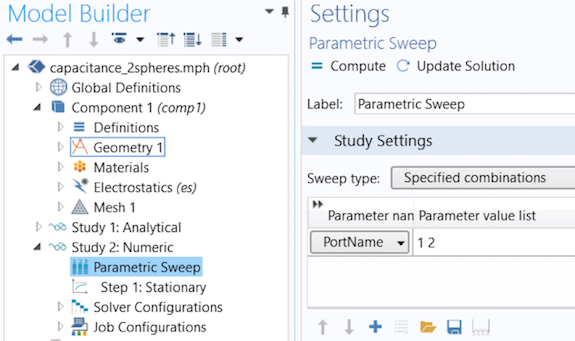
在上述模型中,COMSOL Multiphysics 软件在扫描期间将一个终端设置为 1 V,将所有其他终端设置为接地,从而产生以下两种解: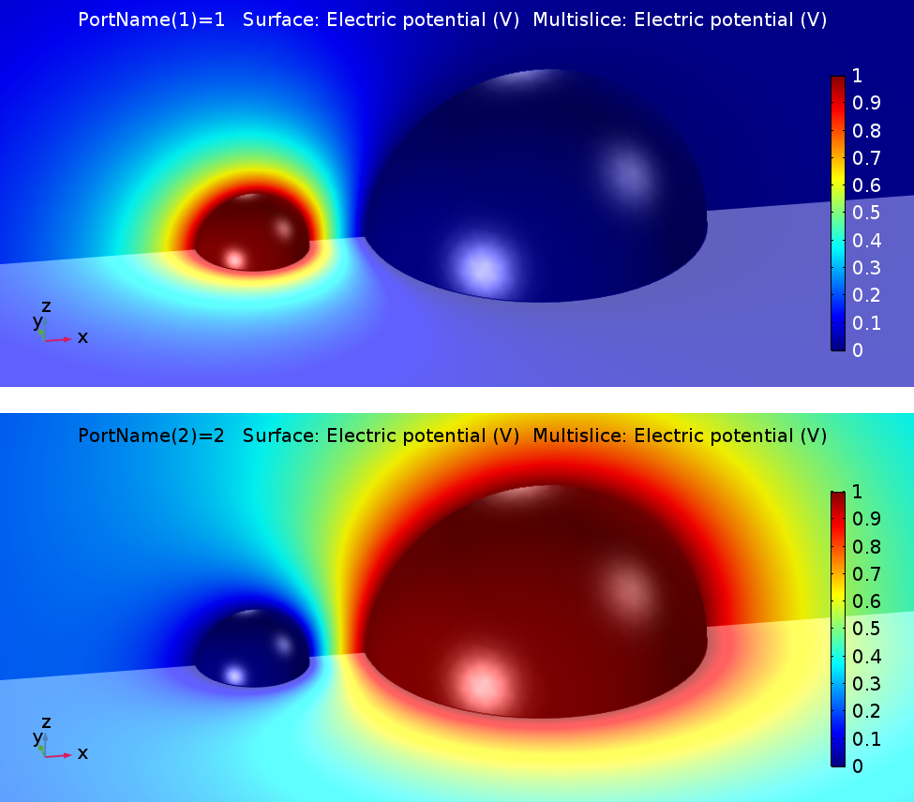
你可以使用结果>全局矩阵计算来提取不同符号的电容矩阵,包括麦克斯韦电容矩阵和互电容矩阵。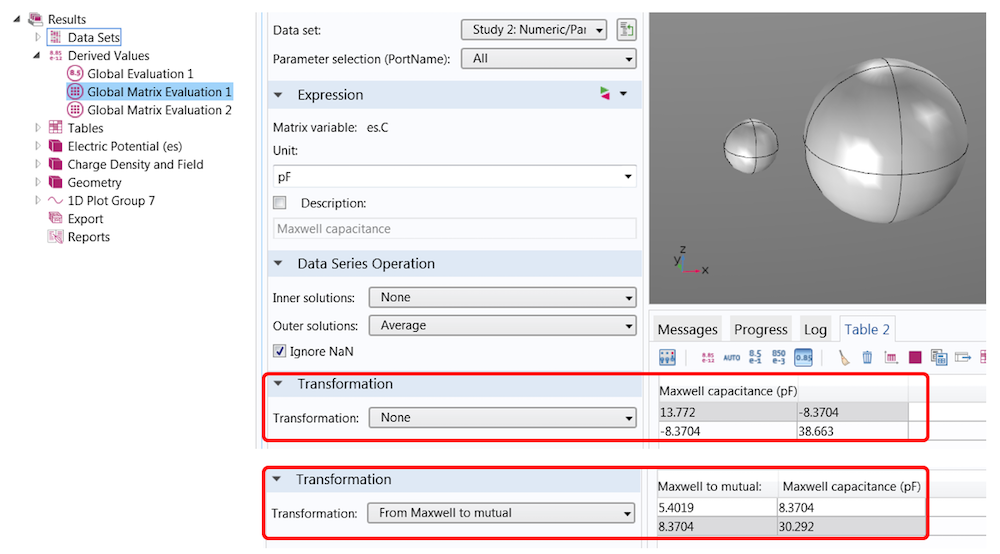
在这个简单的例子中,二者的关系如下
C_{m,21} & C_{m,22}\end{bmatrix}=\begin{bmatrix}c_{11}+c_{12} & -c_{12}\\-c_{21} & c_{22}+c_{21}\end{bmatrix}
如果你设置的是电荷终端而不是电压终端,主要解是反电容矩阵。有一组转换可以帮助你将电荷转换为上述矩阵。
利用稳态源扫描和边界元法提高速度
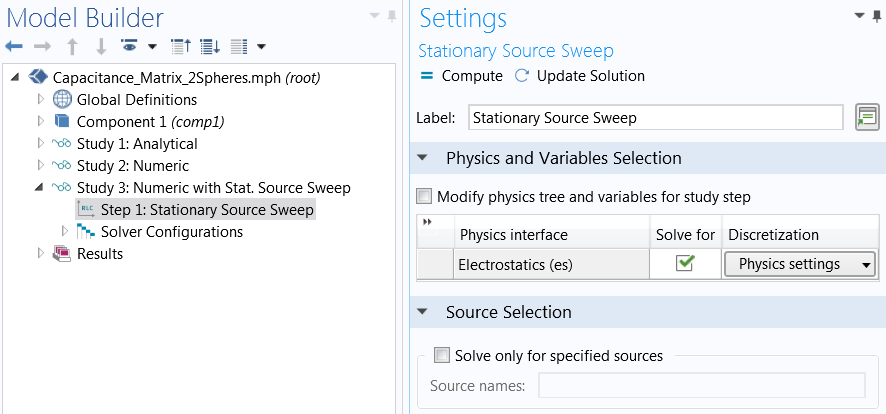
在 COMSOL Multiphysics 5.3 版中,我们引入了许多强大的新建模方法。与电容矩阵计算特别相关的一个特征是新的稳态源扫描研究步骤。
与对PortName使用参数化扫描的手动终端扫描不同,这种新技术说明了这样一个事实:将不同的电荷或电压模式应用于静电系统不会改变基础有限元方程的系统矩阵,只会改变它们的负载。这意味着矩阵只需要反转一次,即可重复用于所有其他负载情况。这种方法可以显著减少计算时间,尤其是当终端数量很大或者需要其他参数化扫描(例如,对于几何结构)的情况。
即使对于中等数量的终端,比如触摸屏模拟器仿真 App,速度的加快程度也是惊人的:对于这个具有相同自由度数量的模型,我可以在我的机器上将速度加快 7.8 倍!
新的电容式位置传感器教学案例使用稳态源扫描研究步骤。
稳态源扫描也更容易设置。无需激活手动终端扫描并定义PortName变量和参数化扫描,你只需要选择一个研究步骤。默认情况下,研究将在所有终端上运行。或者,你可以定义要涵盖的指定源。
如果稳态源扫描如此强大,那么我们为什么要保留传统方法呢?
有些情况下,我们希望重新计算系统矩阵; 例如,在非线性或多物理场问题中,或者应根据每个终端配置调整网格的情况。在这种情况下,采用手动终端扫描方法比较好。
COMSOL® 软件 5.3 版的另一个强大功能是静电中的边界元法(BEM)。与所有域(包括周围空气域)都需要网格的有限元法相比,边界元法避免了无限空间中的网格划分,从而减少了自由度的数量。你可以在使用 BEM 对电容式位置传感器建模教程中了解更多关于静电学中边界元和电容矩阵计算相结合的信息。
迫不及待想了解更多关于新边界元实现的信息?阅读上一篇博客文章,了解这种方法如何帮助简化腐蚀建模。
电容矩阵计算的总结性思考
在本篇博客文章中,我们研究了电容矩阵的计算,讨论了不同的术语,并为一个具有闭合解析解的众所周知的问题提供了一个数值解。这里介绍的简单模型可以为你自己的模型提供参考,而 5.3 版本中发布的新功能可以帮助你更高效地创建具有许多终端和附加参数化扫描的大型模型。
其他资源
- 浏览有关电容和边界元的博客文章:
参考文献
- de Queiroz, A.C.M., 2003, “Capacitance Calculations“.
- Lekner, J., 2011, “Capacitance coefficients of two spheres”,Journal of Electrostatics69(1):11-14.



评论 (3)
锋 张
2021-02-24great!
登锋 祝
2021-12-25thanks
哲 刘
2022-07-05同样的方法建立对极板电容的模型后,无法使用全局矩阵提取麦克斯韦电容矩阵
1.全局矩阵没有预表达式
2.偶尔可以的时候,提取出的麦克斯韦电容矩阵不含C12