
在之前的一个关于弱形式的博客系列中,我的同事 Chien Liu 介绍了稳态问题的弱形式以及在 COMSOL Multiphysics 软件中的实现方法。本篇博文是弱形式系列的扩展,介绍了如何使用弱形式偏微分方程接口求解瞬态问题。下面我们将演示在 COMSOL 中如何操作。
问题举例:一个瞬态偏微分方程
让我们考虑由一维瞬态偏微分方程给出的初始边界值问题
(1)
这个微分方程有边界条件
(2)
和
(3)
以及初始条件
(4)
这个方程只有一阶时间导数,因此,我们只需要为主要变量指定初始值。对于具有二阶时间导数的方程,我们还必须提供速率的初始条件。
等式2中的边界条件是一个 Neumann 条件,通常用于描述机械载荷或热通量。零值意味着没有载荷,或者相当于绝热层。等式3中的边界条件是一个 Robin 或混合条件,通常用于描述弹簧边界或对流热通量(参见上一篇博文中的 Neumann 条件和 Robin 条件部分。
获得瞬态问题的弱形式
推导瞬态偏微分方程的弱形式,与前一博客系列的第 1 部分中稳态问题相同的步骤相同。大致是,首先将偏微分方程写成,对于本文讨论的问题,我们有
接下来,在弱形式上执行;也就是说,将这个方程和任何测试函数 (也称为加权函数)的乘积进行积分都应该为 0。第三,应用导数的乘积法则和散度定理在加权积分中减少(削弱)因变量的最高阶空间导数。在一维中,这可以归结为分部积分,从而给出了弱形式。
因此,将(1)乘以试函数并在域上积分,我们得到
(5)
通过对具有最高阶空间导数的乘积应用分部积分,我们得到
(6)
对于这种弱形式,我们可以结合边界条件来获得
(7)
请注意,时间导数的存在并没有改变我们导出弱形式的方式。在上面的推导中,时间偏导数只是乘以加权函数。弱形式的积分是空间积分,因此,我们对时间导数不做任何分部积分。加权函数只是空间坐标的函数,而未知是空间和时间的函数。
在弱形式 PDE 接口中定义问题
在 COMSOL Multiphysics 中的弱形式偏微分方程接口中定义瞬态偏微分方程的弱形式包括以下三个步骤:
- 输入域贡献
- 输入边界条件
- 定义初始条件
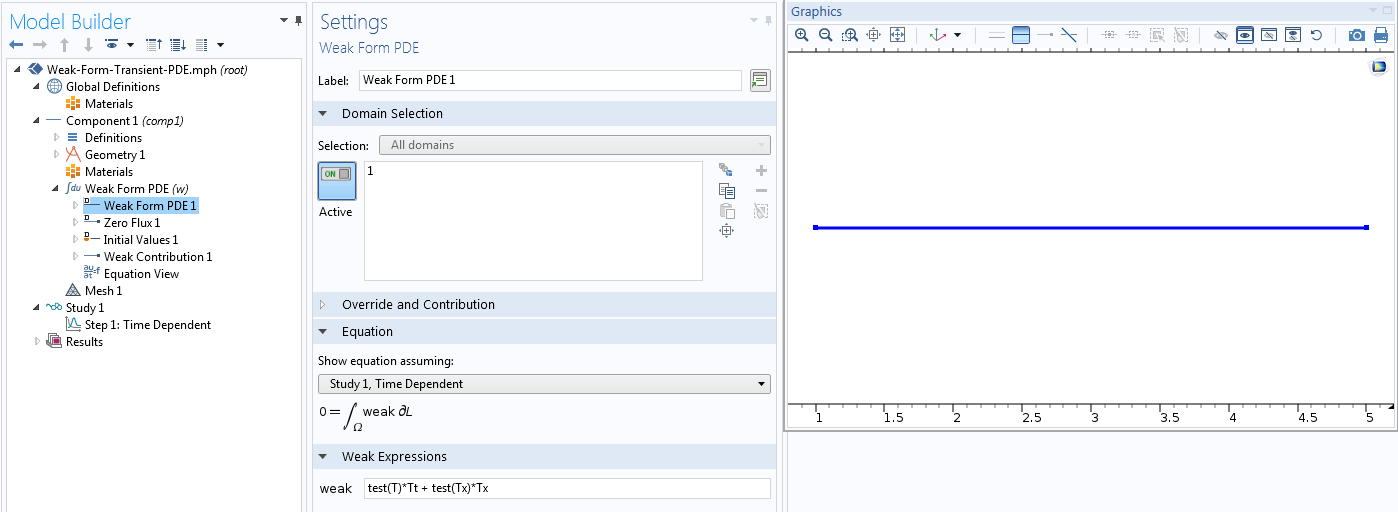
在弱形式PDE 1节点的设置窗口的输入域的弱表达式字段。对于我们的问题,这是test(T)*Tt + test(Tx)*Tx,其中test(T)表示加权(试)函数,它对应于因变量。还有Tt和Tx分别是因变量的时间和空间偏导数。
可以使用内置边界条件或边界处的弱贡献来定义边界贡献。出于教学演示上的原因,我们将使用后者,尽管今天的问题中的边界条件可以使用内置的通量/源节点。
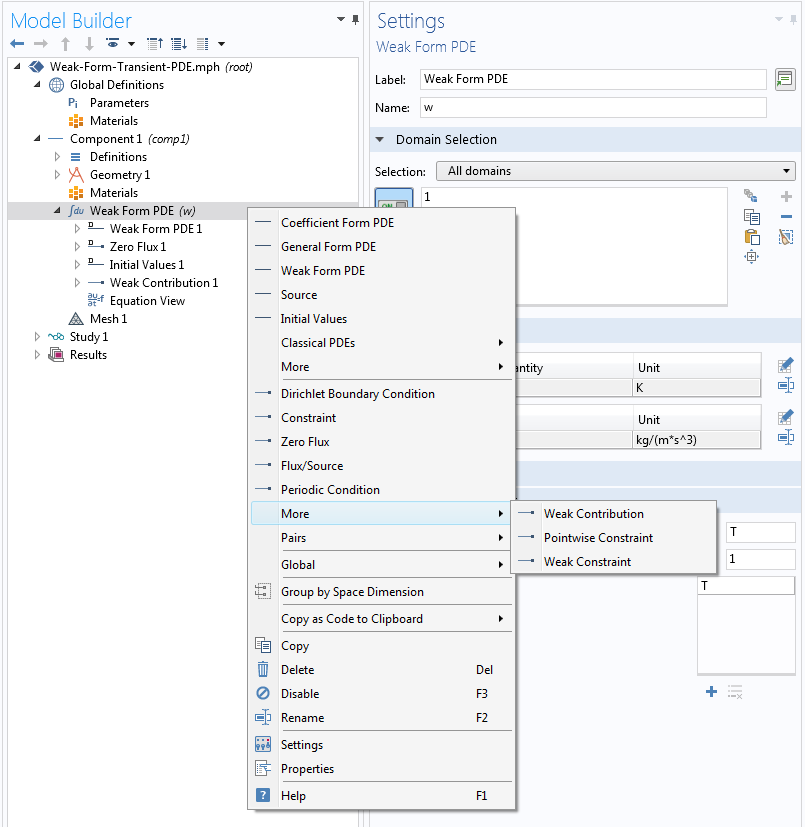
边界条件的实施。
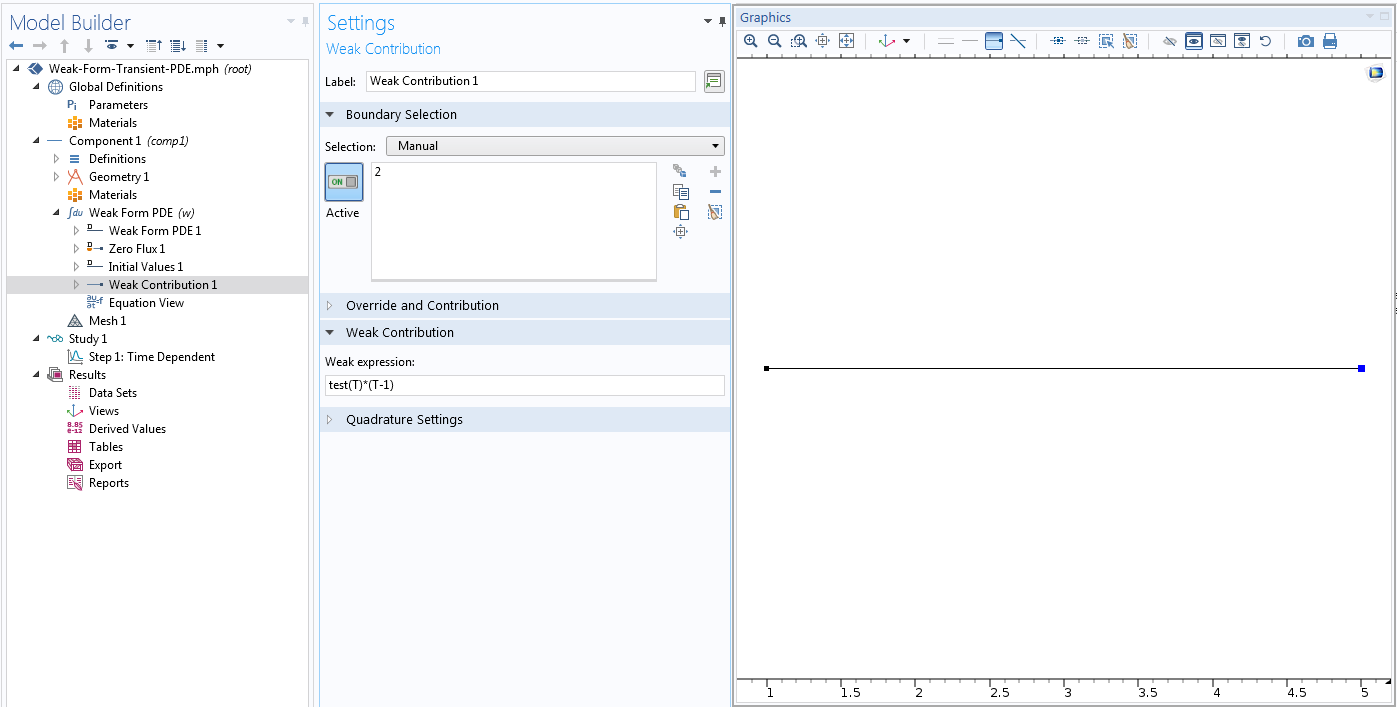
来自左边界的贡献为零;我们不用做任何操作。右边界的贡献是弱形式方程(7)的第二项,可以按下面的方式输入。在边界选择窗口中选择点 2 并在弱表达式字段输入表达式test(T)*(T-1)。
最后一个部分是初始值。我们的问题只需要因变量的初始值。因此,我们只需要在初始值的设置窗口中填写第一项。在我们的例子中,我们正在考虑一个统一的初始值。如果不是这个例子,可以键入包含空间坐标的表达式或函数,而不是数字。
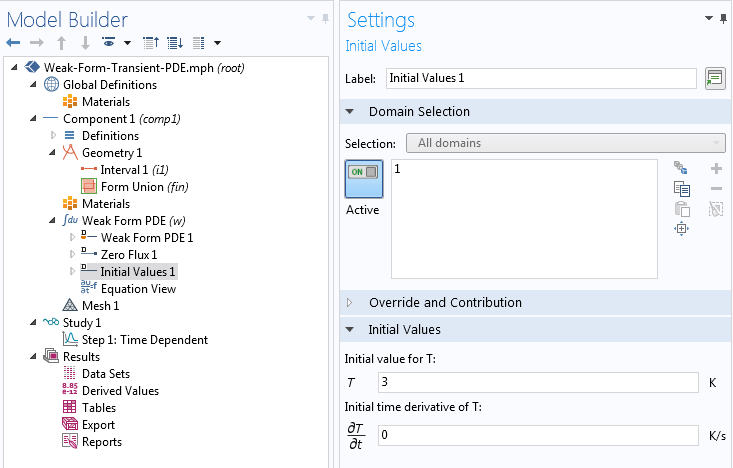
初始条件的执行。
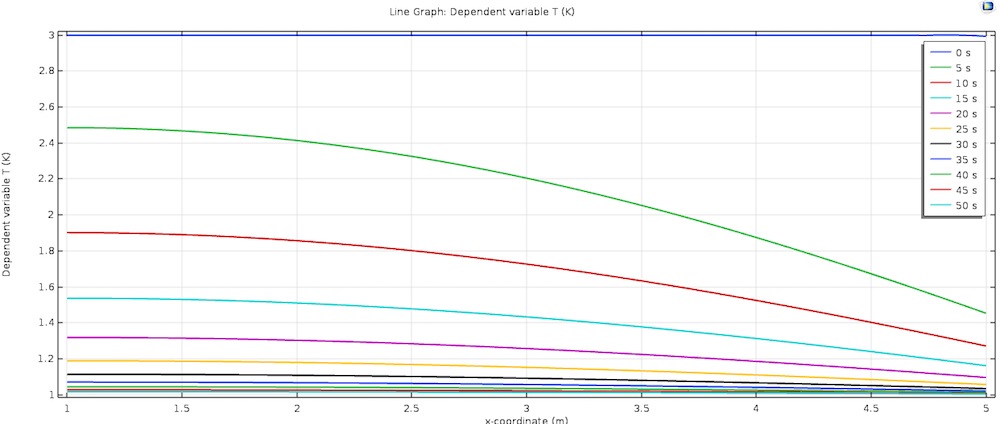
现在,我们已经定义了偏微分方程、边界条件和初始条件,剩下要做的就是在研究设置中定义求解此问题的时间间隔,并点击计算按钮。模拟运行的时间范围为,不同时间实例的解决方案如下所示。
推导的弱形式背后的内容
我们在上面推导出并在 COMSOL Multiphysics 接口中定义的弱形式是一个连续问题。该函数基于在弱形式 PDE 界面的设置窗口的离散化部分中选取的形状函数。在内部,将使用有限元插值函数进行离散化,插值函数阶次在弱形式偏微分方程接口的设置–离散化部分定义。例如,对于拉格朗日插值函数,解近似为
这里,N是有限元网格中的节点数,\phi_i, i=1\dotsc N是定义的形(插值)函数。
如果我们把上式代入弱形式,我们会得到关于节点解的常微分方程组。所有的空间导数都指向已知的形函数。这个常微分方程组由 COMSOL Multiphysics 内置的时间积分算法求解。(注意:我们的问题定义中不需要做任何时间离散化;这将在内部特别处理。这部分仅供参考。) 如果问题是稳态的,方程组是节点未知数的代数方程组。这一次,节点未知数不是时间的函数。要了解有关离散化的更多信息,请查看以下关于形状函数和相关离散化的博文。
关于获得瞬态问题弱形式的总结性思考
在这篇博文中,我们演示了如何使用弱形式偏微分方程接口求解瞬态 PDE 方程。瞬态问题的弱形式的推导过程与稳态问题完全相同,并且也使用相同的接口。我们只需要指定问题的连续性。在内部,空间离散化是基于弱形式偏微分方程接口设置窗口中的离散化的定义,时间离散化是根据软件选择的默认时间积分算法来完成的。如果我们有一个好的理由,我们可以转到求解器配置节点。问题的定义保持不变,因为我们指定的是连续性,而不是离散性。
进一步阅读
在这个博客系列中了解关于弱形式的更多信息:



评论 (4)
Zheng SiZheng
2021-08-01请问如何在PDE弱形式的模块下,使用用户自定义材料?
yongchao wang
2021-08-11 COMSOL 员工Zheng SiZheng, 您好!
可以参考博客://www.denkrieger.com/blogs/brief-introduction-weak-form/ 中的热通量方程,方程中的截面积及热导率的乘积定义为1,对于一维实际情况q(x)=-A*k*ΔT,其中A为横截面积,k为导热系数;此方程右侧写成弱形式为-A*k*Tx*test(Tx),此时材料的属性已经在弱形式中。弱形式中相应的变量可以为自定义的材料属性。
玉平 姚
2022-03-28请问,在PDE模块里面如何添加周期性边界条件呢?比如floquet周期性边界条件
Kaixi Tang
2022-04-02 COMSOL 员工你好,软件内周期条件中是有内置的floquet周期选项的,博客下不提供PDE技术支持,谢谢。