电阻效应和电容效应是理解电化学系统的基础。由质量传递而产生电阻和电容,可通过描述对应基本现象(例如扩散)的物理方程来进行表征。此外,当需要考虑双电层、薄膜和反应动力学的电阻或电容特性时,可利用与电化学电流及电压相关的物理条件对此类效应进行简化处理。最后,您可以在 COMSOL Multiphysics® 中轻松地对来自外部负载电路的电阻和电容进行表征。
什么是阻性电流和容性电流?
在描述电路的性能表现时,我们经常会提到电阻和电容。通过阻值为R(Ω) 的电阻器的电流与外加电压V成正比,通过电容值为C(F) 的电容器的电流与电压变化率成正比:
在电化学电池中,我们可以通过外加电压来测量电流,反过来也同样可行。因此,人们常常从电阻和电容的角度来研究电池的响应。在交流阻抗分析中,阻性电流与外加电压同相,而容性电流与外加电压不同相。虽然我们可以基于测量数据推算电阻和电容,但是许多物理效应都会增加电流的测量值。更有效的方法是对描述电阻和电容效应产生过程的方程式进行求解,方程的结果能帮助我们透彻地理解其中的物理过程。我们使用仿真作为分析测量数据的手段,并结合底层物理原理来进行解释。
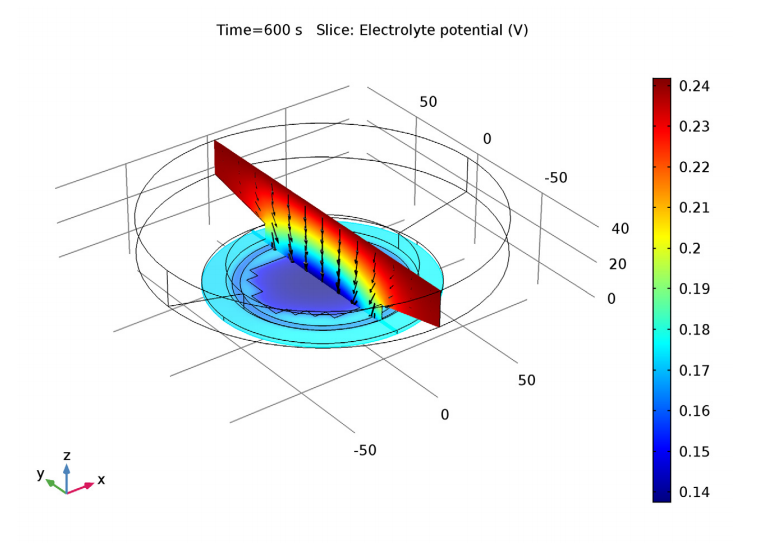
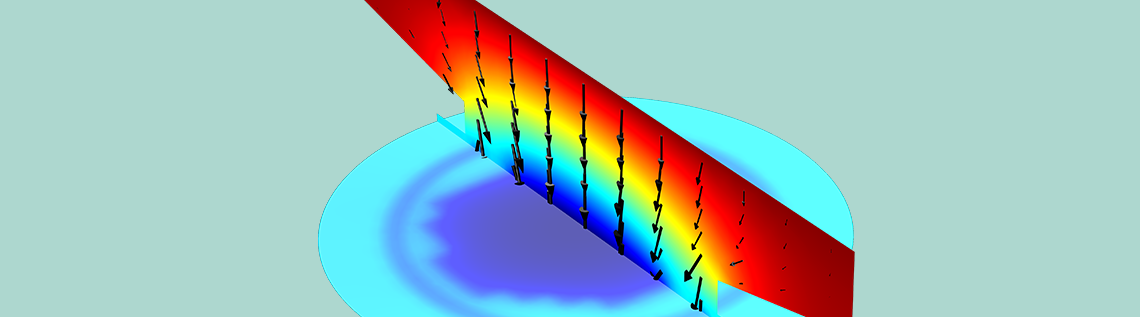
电解质电位图(颜色图)显示了在用于掩膜圆晶片镀铜的电镀槽中,与阻性电流(黑色箭头)相关的电压。镀层的电阻变化也包含在了模型中。
产生电阻和电容的电化学效应
由于电解质的导电能力有限,因此电化学电池中经常需要考虑电阻效应。为了使电流能够通过电极,需要在阴极和阳极之间施加一定的电压,这与使用了常规电阻器的电路是一样的。COMSOL Multiphysics 中的一次电流分布和二次电流分布物理场接口可以求解欧姆定律,并据此预测外加电压的大小(通常被称为电阻降),其数值与电解质电导率和电极几何结构之间存在函数关系。
如果无法忽略电极反应动力学的影响,则需要引入额外电压(称作过电位),以抑制发生在电极表面的电化学反应的活化能。常见的电极反应动力学速率定律(例如 Tafel 定律或 Butler-Volmer 方程式)是以过电位的形式对电流密度进行定义的——这里的电流-电压关系可以解释为电阻。然而,与电路中简单的电阻器不同,由电极动力学引起的电阻通常是非线性的。这一点体现在了 Tafel 定律中,即过电位与电流密度的对数成正比。只有外加电压的变化幅度非常小时,电流-电压关系才会呈近似线性,例如电化学阻抗谱。
在电分析和阻抗谱中,人们通常基于电阻和电容的测量值来研究由扩散引起的质量传递。在传统的等效电路分析中,可利用 Warburg 阻抗来解释人们观察到的、由扩散引起的效应。类似地,人们通常使用Randles 电路来描述上述所有效应的集合,即扩散、电极动力学和溶液电阻。
不过,我们也可以利用对应的物理方程式来直接描述动力学和扩散对电化学电池性能带来的影响。在电分析接口中,我们对菲克扩散定律与电极动力学关系式(例如 Tafel 或 Butler-Volmer 方程)同时进行求解,直接计算出了基本电化学过程的阻抗谱。在三次电流密度接口中,除了扩散之外,质量传递阻抗还可以引入迁移和对流的贡献。
如果您希望了解在不使用等效电路的情况下,根据物理方程式对电化学阻抗谱进行预测的示例,请参阅电化学阻抗谱教程和锂离子电池案例。
膜阻
当处理电极-电解质交界面上薄层或表面膜的特性这一重要因素时,也需要引入电阻和电容效应。在这些情况下,直接以电阻或电容的形式来表示其特性往往会更简洁明了。
由于电极表面与电极内部的电导率差异较大,因此只要在电极表面创建一个材料薄层,便会产生膜阻。这种额外的阻抗可能导致系统效率降低。如果膜阻出现在电池中,由电化学反应产生的电池电压便会下降,也就是说,外部电路可用的电能变少了。
当暴露在空气中时,大多数金属表面会迅速氧化,直到被一层金属氧化物覆盖。一般来说,金属氧化物比原来的金属导电性更差,由此向系统中引入了额外的膜阻。海底腐蚀便是这种情况,具体情况可参考阳极膜阻效应的案例。
另一个与膜阻相关的示例是电沉积,在此类情况中,电极体材料和表面沉积物质不同。当电导率不同、厚度逐渐增加的物质层在电极表面沉积时,电极表面与电极内部材料属性不同。
在 COMSOL Multiphysics 中,可在电极表面对膜阻进行定义。最直接的方式是设置给定的膜阻,单位为 Ω·m2。单位中包含了 m2,说明了此单位须用来表示单位为 A m-2、垂直于薄膜的电流密度的局部电阻,薄膜中可驱动电流的电势差单位为 V。另一种方式是我们输入参考膜厚、膜厚变化和薄膜电导率。当薄膜厚度随时间变化时,这些数据将十分有用。
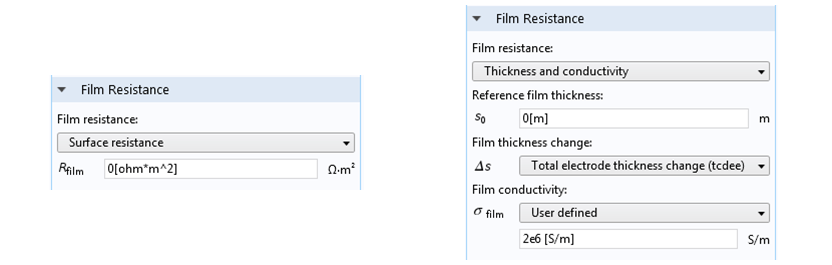
膜阻的设置。左图:电极的表面形状和成分恒定不变、膜阻为常数的情况。右图:在电沉积正在进行时,仿真中的薄膜厚度会发生变化,这是更常见的情况。
双电层电容
带电电极和电解质之间的交界面处会产生被称为双电层(electrical double layer,简称 EDL)的区域。在这块区域中,电荷间的吸引和排斥会导致离子浓度的分布相当不均匀。(在即将发布的博客文章中,我们将更详细地讨论 EDL 的物理场和建模知识。同时推荐您阅读一篇介绍电池中的电流流动的博客文章。)
通过随时间变化的外加电压来改变电极电位,会在双电层中积累或释放电荷。人们使用双电层电容来描述双电层中积累的电荷量。双电层的尺寸取决于系统中的 Debye 长度,通常为纳米级。相比之下,扩散层或电化学电池的尺寸范围通常在微米到米之间,因此这类电容可以被视为在电极-电解质交界处发生的表面效应。
在 COMSOL Multiphysics 中,您可以使用多种 EDL 建模工具(请参照带电荷传递的扩散双电层教学模型)。COMSOL Multiphysics®5.2a 版发布了全新的Nernst-Planck-Poisson 方程多物理场接口,让建模变得空前简单。不过,即使相关的理论成果十分丰富,但设计一个能精确描述 EDL 中实验观察现象的模型仍是无稽之谈。因此,我们优先考虑双电层电容的经验描述,即通过拟合实验数据凭经验定义电容。
在阻抗谱中,高频下电压会迅速变化,因此双电层电容尤为重要。有限的电极反应速率、有限的质量传递速率,再加上双层电容,许多电化学系统的奈奎斯特图常出现的“半圆加尾巴”的特征形状与三者紧密相关。
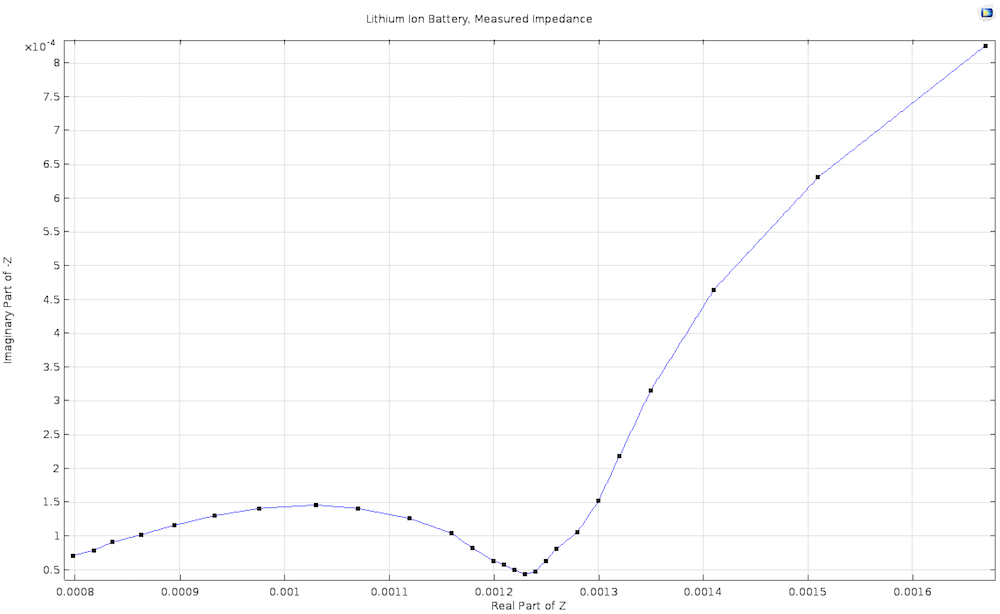
锂离子电池的实验测量奈奎斯特图,来源于锂离子电池的阻抗演示 App。
在定义电极表面时,我们可以添加一个双电层电容子节点。为了建立这一电极特征,我们须输入单位面积的表面电容(单位为 F m-2),不过某些情况下还需要额外的输入。以多孔电极为例,多孔基体双电层电容特征需要输入一个具体表面积,以确定电极-电解质交界面的真实表面积,而我们知道,这个交界面上存在着双电层,并且发生了电容性充电。除此之外,您也可以使用内置工具,根据球体、圆柱体或薄片的粒子属性来计算多孔电极的双电层面积。在这种情况下,您不需要明确了解电极的具体表面积。
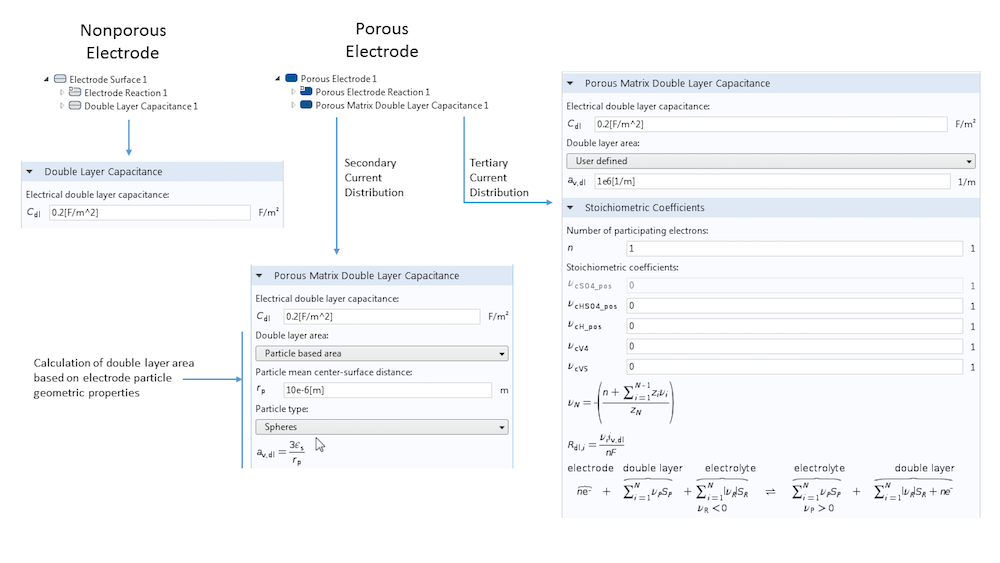
“双电层电容”特征的设置概览。图片显示了无孔电极和多孔电极之间的差异,以及根据某些基本几何属性来计算双电层表面积的可能性,而没有直接将表面积添加为输入的方式。
解决更复杂的电路设置
在少数情况下,建议您将电极连接到更复杂的电路,借此更加清晰地了解电化学系统如何与复杂的驱动电路耦合。COMSOL Multiphysics 再次表现了出色的灵活性,可以将任何电化学物理接口连接到电路接口。
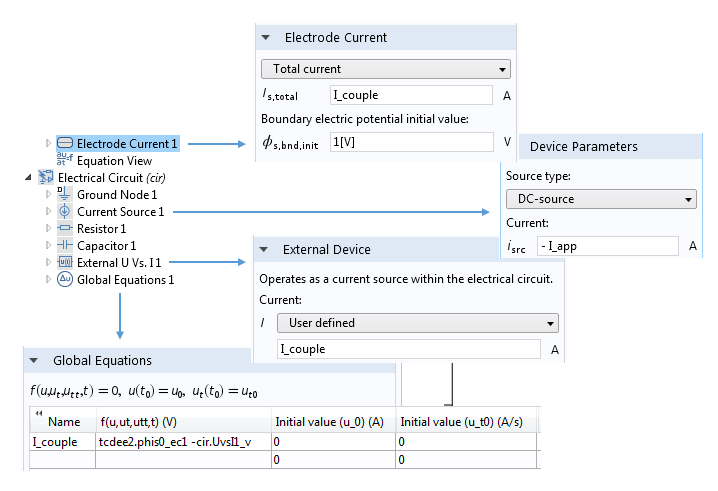
将电流驱动的电化学系统耦合到提供电流激励设备的电路,上图显示了此系统的常规设置。需要特别注意的是电极电流和外部设备栏中的电流如何被设置为了共用变量I_couple。我们对与这两个节点相关联的电压施加约束,使二者相等,由此确定上述变量的值。
通过精确描述电阻和电容提高电化学模型的准确性
在本篇博客文章中,我们解释了如何描述电化学系统的电阻和电容,并详细介绍了每种方法的适用情况。我们建议您将本文中介绍的工具和知识用于实际的建模工作,帮助您最大限度地提高电化学模型的准确度和实用性。
在 COMSOL Multiphysics® 中模拟电化学系统的其他资源
- 如需了解如何在电化学模型中添加电阻和电容特征,请下载以下教程:
- 观看已归档的网络研讨会,了解更多有关在 COMSOL Multiphysics 中模拟电化学系统的信息



评论 (0)