
1875 年,John Kerr 将载流线圈放置在玻璃板两侧的孔中,从而产生了电场。当一束偏振光穿过平板后,他发现偏振是不同的。这种差异与玻璃折射率的变化有关,折射率与电场的平方成正比——这种现象被称为磁光克尔效应(Kerr effect)。今天的博文将带您了解如何对这种效应以及其他线性和非线性现象进行建模。
理解非线性光学材料的磁化率
当给介电材料施加电磁场时,电磁场会将材料中的电子从其原始轨道上迁移,使电子以特定的频率振荡。换句话说,磁场使材料极化。在这种情况下,位移场用外加电场的函数表示,如下所示:
其中,E是施加的电场矢量,P是极化矢量,\epsilon_0是真空介电常数,\chi_0是各向同性磁化率。
对于各向异性介电材料,极化矢量是磁化率张量的函数,如下所示:
\chi_{11} & \chi_{12} & \chi_{13} \\
\chi_{21} & \chi_{22} & \chi_{23} \\
\chi_{31} & \chi_{32} & \chi_{33}
\end{bmatrix} \textbf{E}
最后,对于非线性介电材料,感应极化可以通过介质的磁化率(\chi)表示为介质内电场的函数,并如下所示:
{(1)}(\omega)E(\omega)\chi^{(2)}(\omega)E^2(\omega)\chi^{(3)}(\omega)E^3(\omega)+ . . .)
其中,E是外加电场,ε0是真空介电常数,\chi^{(i)}是一阶磁化率。
假设不存在独立于E的极化。要对非线性项的极化进行彻底的推导,请参阅 Y. R. Shen 的书(参考文献5).
光学材料的一阶磁化率
一阶磁化率(\chi^{(1)})涉及由束缚和自由载流子(如电子)的偶极振荡引起的折射率变化。Hendrik Lorentz 最初提出了创建一个数学振荡器模型的想法,该模型可以将束缚电子的偶极振荡与材料的磁化率联系起来。Paul Drude 提出了半导体内部振荡的概念,这种振荡处理的是材料内部的自由载流子。结合了束缚载流子和自由载流子效应的新模型被称为Drude-Lorentz< 模型。
在 COMSOL Multiphysics®中,Drude-Lorentz 模型可用于定义材料的相对介电常数。要定义 Drude-Lorentz 模型,需要将高频下的相对介电常数、等离子体频率、共振频率和阻尼系数作为输入给出,如下所示。在分配每个振荡器的贡献时,也可以添加多个振荡器。
其中,εr是材料的复相对介电常数,ε∞是带间跃迁对介电常数的贡献,ωp是等离子体的频率,Γ是阻尼系数。
模拟等离子体波导滤波器
为了展示 COMSOL Multiphysics 在建立 Drude-Lorentz 材料模型方面的能力,我们对具有金属-绝缘体-金属(MIM)界面的波导进行了建模。这里,金属和绝缘体分别被建模为银和空气。在这种结构中,绝缘体的宽度沿波导周期性变化(见下图)。绝缘体的这种特殊排列使波导管像一个等离子体波导滤波器一样工作。
这个例子表明,波导阻止了波长在 1.4um 和 1.6um 之间的电磁辐射,但允许其余波长(见下图)。银材料可以用 Drude-Lorentz 来近似建模,ε∞= 3.7,ωp= 13.8 rad/s,以及Γ= 2.736rad/s,而绝缘体使用空气建模。作为 Drude-Lorentz 材料模型近似的替代方法,由 Johnson 和 Christy 的实验数据(参考文献4)确定材料的属性,该材料在材料库中以Ag (Johnson)的形式提供。
请注意,这种等离子体波导滤波器的输出特性类似于光纤布拉格光栅(FBG) 配置的输出特性。

等离子体波导滤波器示意图。蓝色和灰色分别是绝缘体和金属域。虚线描绘了周期性重复的单胞。
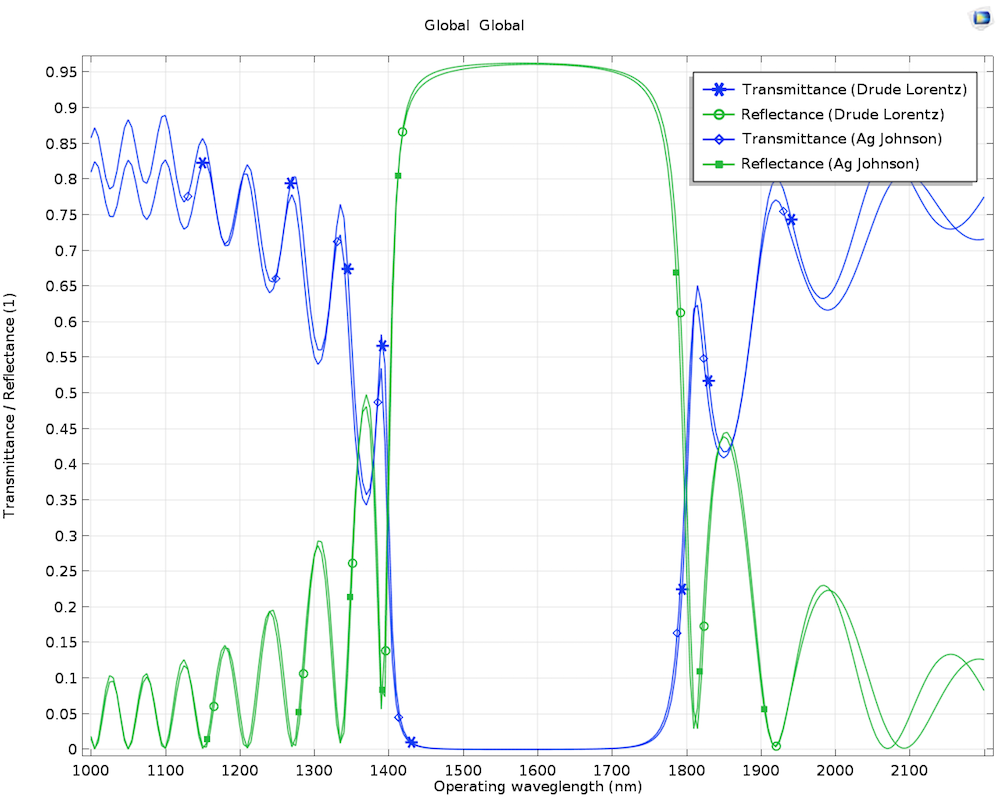
使用 Drude-Lorentz 模型和 COMSOL 材料库中的 Ag (Johnson) 模拟的通过等离子光栅滤光器(具有 10 个晶胞)的透射率和反射率。你可以从 COMSOL 案例库中下载这个模型的 MPH 文件。
光学材料的二阶磁化率
有些非线性晶体具有相对较高的二阶磁化率 (\chi^{(2)})。当一束单色光穿过这种非线性晶体时,输出频谱不仅显示出原始频率(ω),也显示出二阶谐波频率(2ω)。因此,这种现象被称为二次谐波生成(SHG)。
SHG 被应用于激光设计和工程领域,在这个领域,很难找到一种材料来发射比入射波长波长更短的光。例如,当红外光源(1064nm)通过磷酸二氢钾(KDP)晶体泵浦时,晶体会发射出绿色(532nm)的激光源。
在 COMSOL Multiphysics 中,这种方法可以用瞬态或频域分析来建模,其中使用非线性系数(d)定义极化,如下所示。在高斯光束的二次谐波产生教程模型中,需要将与电场相关的非线性项引入电位移场 (D)中。在这个模型中,引入非线性项的方式是通过巧妙使用残余电电位移(Dr)。事实上,残余电位移也可以接受一个非线性场量,这里涉及到一个电场分量的平方。这种方法显示了和频生成以及差频生成。
其中,D_r = d_{33} E_{z}^2,d_{33}是非线性系数,Ez是z-电场的分量。
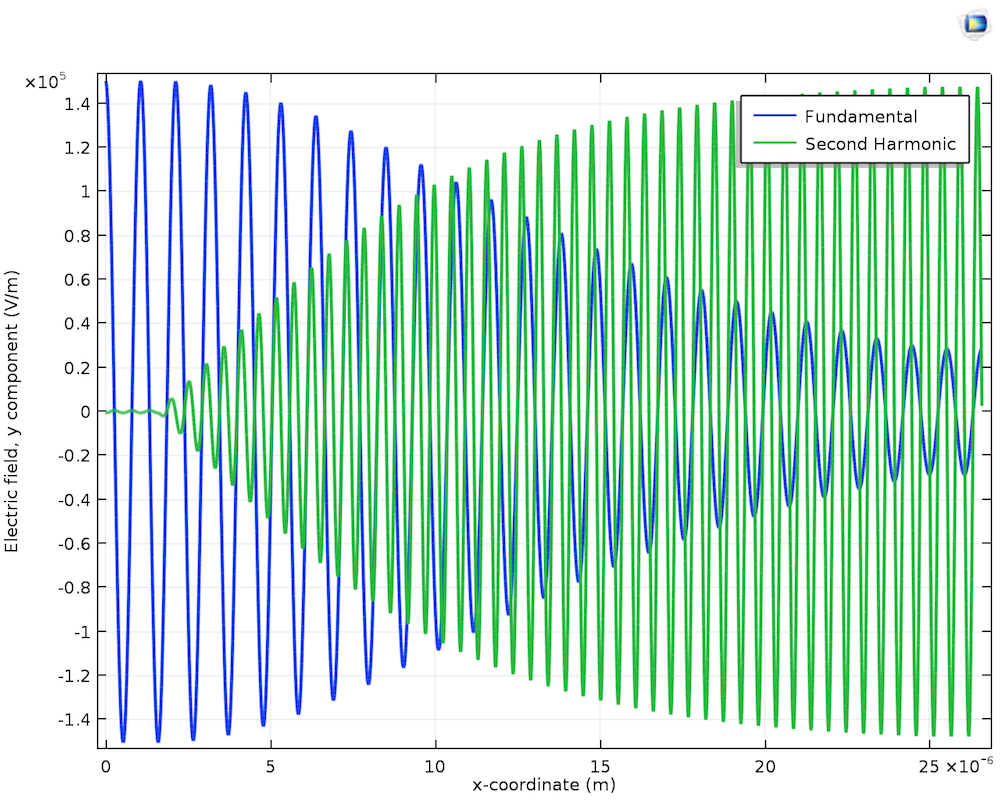
在高斯光束的二次谐波产生教程模型中,只能分析一个特定的频率。(换句话说,用亥姆霍兹方程只能分析一个频率。)因此,该模型建立了两个接口,并耦合了两个物理场。第一个界面代表基波,第二个界面代表二次谐波频率。第一个界面的极化P_{1y},以及第二个界面的极化P_{2y},可定义如下:
其中,d是非线性系数,E_{1y}
是y-基频电场分量,E_{2y}是y-二次谐波频率下的电场分量。
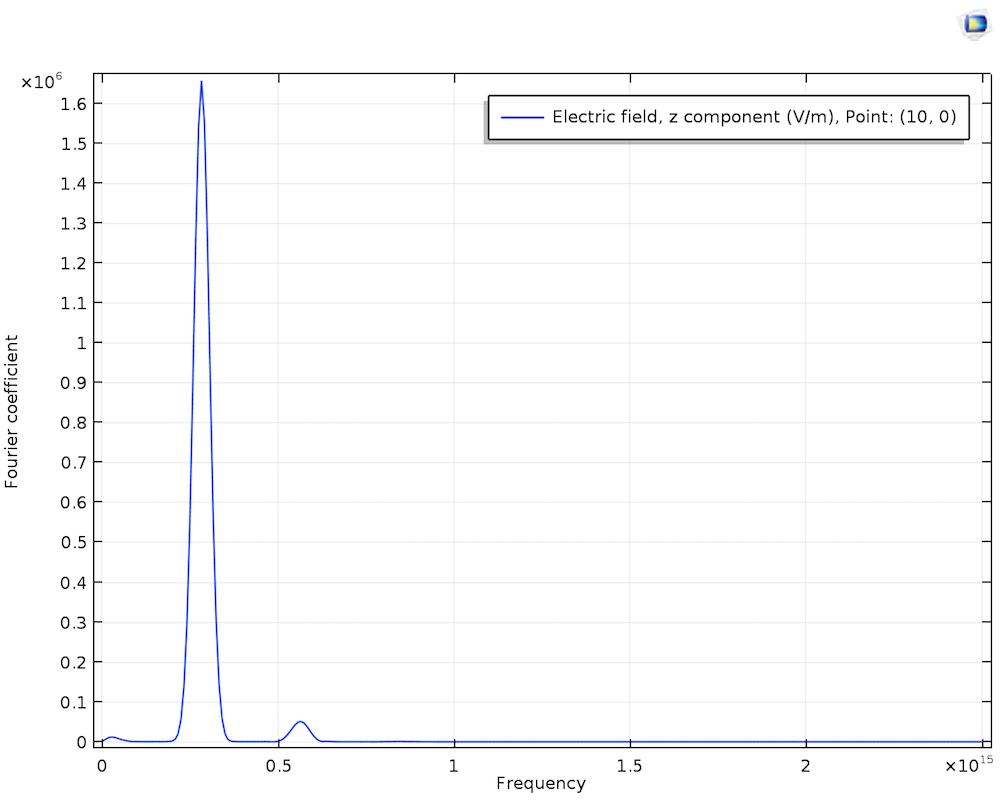
左:输出频谱。大峰左边的小峰表示差频产生,右边的小峰表示 SHG。右:基波和二次谐波的电场 y-分量。
光学材料的三阶磁化率
具有显著三阶磁化率的材料(\chi^{(3)})显示出诸如光学克尔效应、自相位调制、交叉相位调制、三次谐波生成和四波混频等现象。为了说明COMSOL Multiphysics 中的光学克尔效应,高强度(GW/cm2)单色光束(例如 Nd:YAG 激光源)通过由 BK-7 制成的非线性晶体传播。由于 BK-7 中占主导地位的三阶材料非线性,折射率随单色输入光的光束强度(I)的函数变化如下:
其中,n0是折射率的常数(线性)部分,γ是非线性折射率系数,I是光束强度。
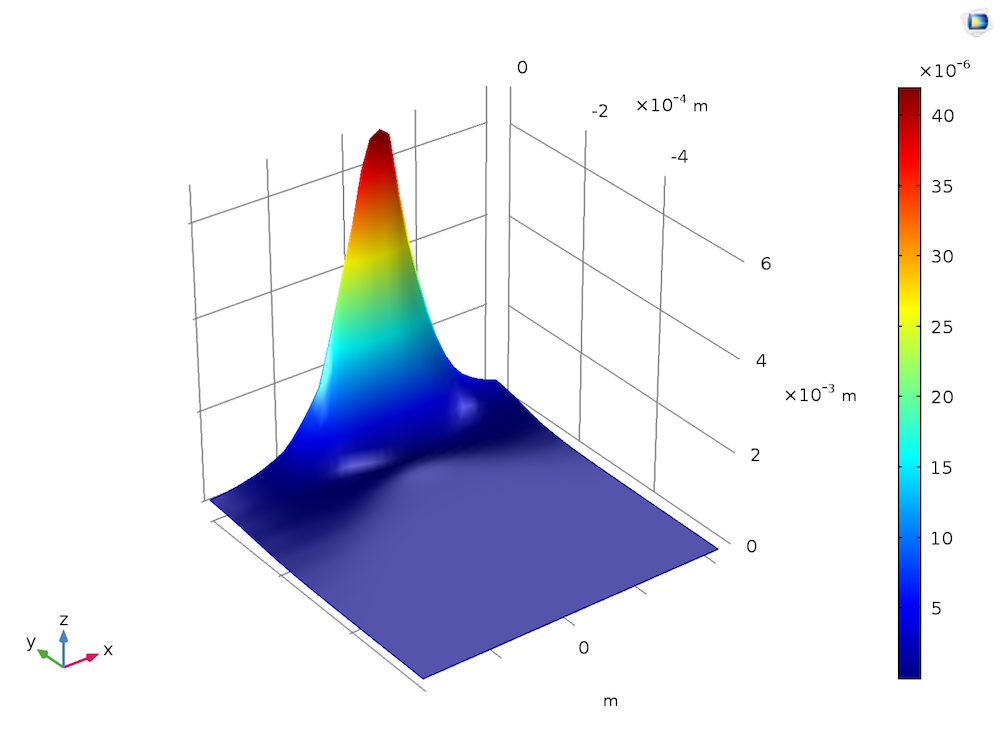
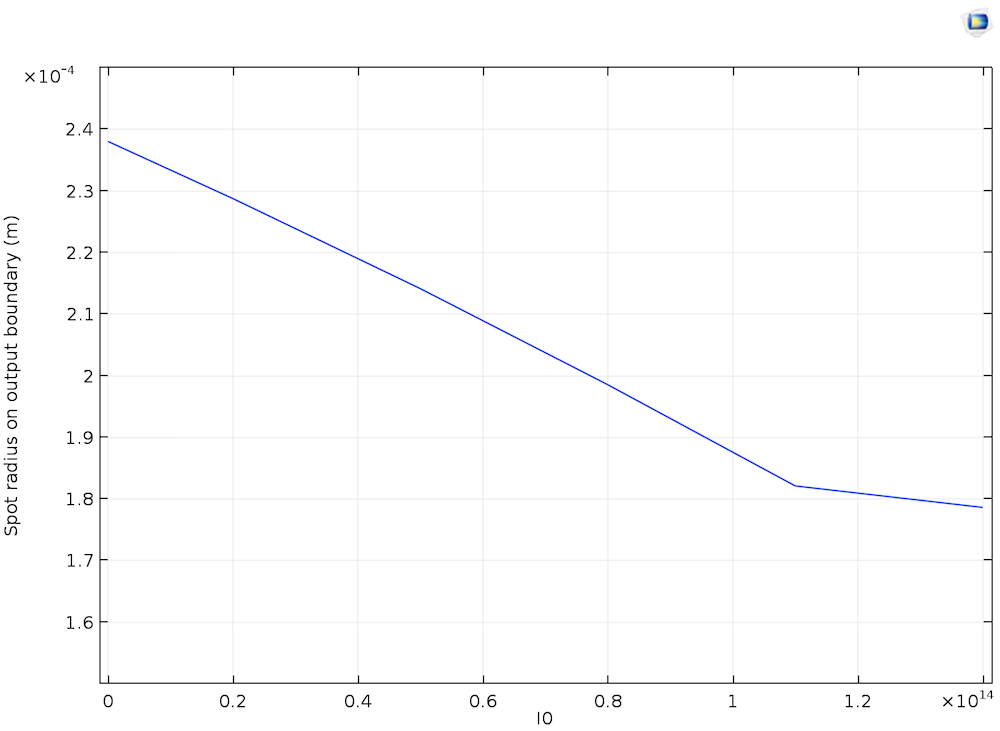
空间高斯发射的光束产生了折射率的空间高斯分布,峰值在中心并径向向外减小。这种折射率分布使得光束在穿过晶体的过程中更加集中在中心。这种现象被称为自聚焦,特别是因为源光束自身的聚焦。这种效应在激光工程中特别有用,在激光工程中,高功率光源在如此狭窄的中心区域中的自聚焦会永久性地损坏晶体,因此需要在设计过程中对这些效应进行建模和补偿。
左: 高峰值强度γI,I0= 14GW/cm2时的诱导折射率变化。右图:传播域末端的光斑半径与峰值强度的关系。
具有电光效应的材料
如本篇博文的引言中所述,有些材料的介质折射率可以是外加电场的函数。该施加的电场可以来自直流电势,或来自通过附着于材料的线圈或接触垫施加的缓慢变化的谐波电势。这里我们开始考虑折射率光学材料特性,而不是磁化率 χ。
从数学上讲,折射率可以表示为外加电场的泰勒级数展开。
对于电光材料,折射率可以转换为以下值:
d_2 n^3 E^2 + . . .
其中,n是没有施加电场的材料的折射率,而d1和d2是电光系数。
关于泡克耳斯效应(Pockels Effect)
如 KDP、铌酸锂(LiNbO3)、碲化镉(CdTe) 等晶体具有上面占主导地位的第一项和第二项的折射率。这种介质被称为泡克耳斯介质(Pockels media),其中,d1被称为线性光学系数,因为折射率是电场的线性函数。
在 COMSOL Multiphysics 中,我们使用光学调制器演示了泡克耳斯效应。在这个模型中,光通过一个单硅波导传播,该波导分为两个波导。如下图所示,在上支路上施加一个接触垫,并用直流电压激励。波导的这个分支也可以被定义为d1=30e-12m/V 的泡克耳斯介质。
当不对接触垫施加电压时,光通过上分支和下分支畅通无阻地流动,并在分支合并在一起的点相长干涉。然而,当向接触垫施加特定电压时,在接触垫内的区域中产生局部电场。在外部电场影响下,该区域的材料特性改变了该介质的折射率,进而有效地改变了光通过上部波导传播的速度。当这些在上部和下部分支中传播的光在分支合并处相互干涉时,会导致相消干涉,没有光向前传播。
泡克耳斯效应的潜在应用是设计光开关。例如,在光子集成电路领域。在COMSOL的教程模型中,我们演示了一种特殊的光开关元件,称为马赫-曾德尔调制器。
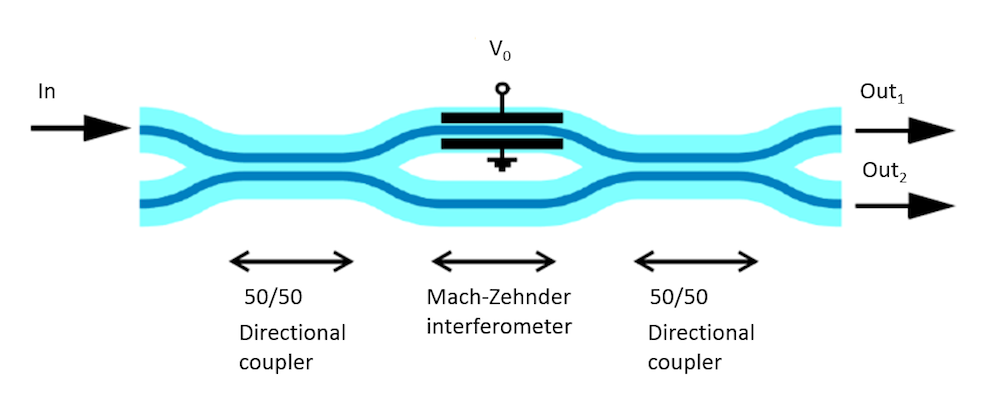
马赫-曾德尔调制器示意图。
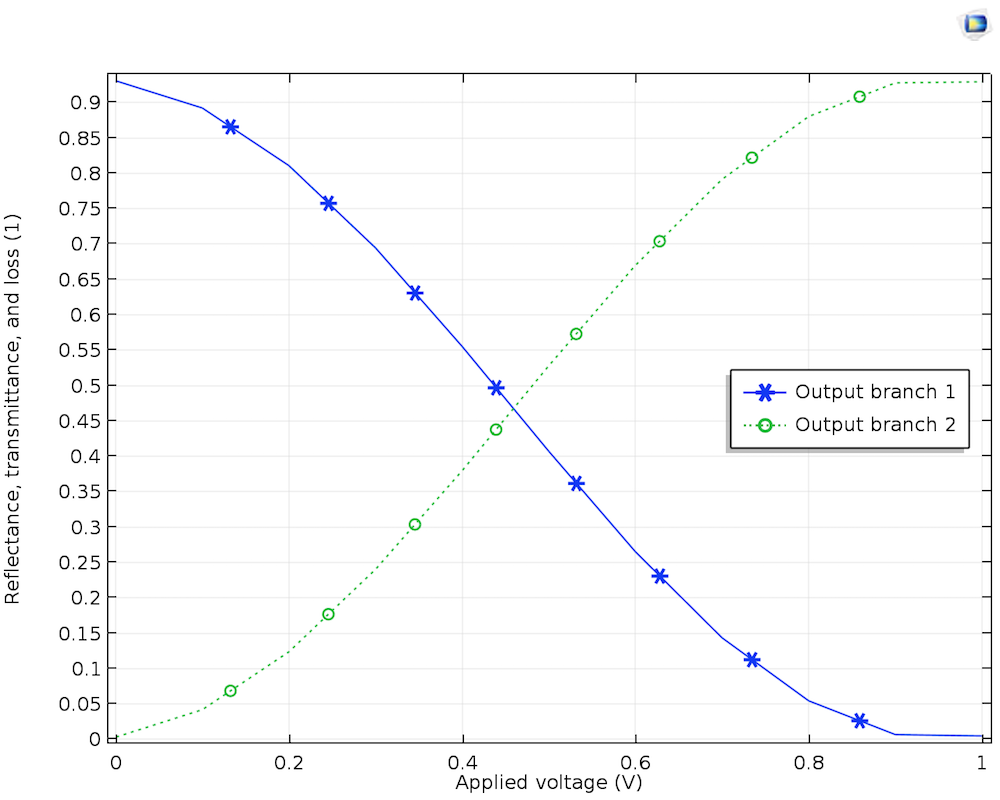
上输出支路 1 和下输出支路 2 的传输与施加的直流电压的关系。
关于克尔效应
某些气体、液体和晶体表现出中心对称性质,其中泰勒展开的第一项和第三项占主导地位。在这种情况下,折射率可以定义为所施加电场的二次函数,如下所示:
线性和非线性光学建模的总结性思考
本文讨论了不同的光学材料,如 KDP、BK-7、LiNbO3、CdTe 和外电场下的硅。这些材料表现出不同的线性和非线性现象,例如 SHG 效应、自聚焦效应以及线性和二次电场效应。我们还研究了这些材料在激光工程领域、滤波器设计和光开关中的应用。
下一步
尝试自己动手模拟这篇博文中介绍的教程:
参考文献
- J. Leuthold, C. Koos, and W. Freude, “Nonlinear silicon photonics”,NaturePhotonics, vol. 4, pp. 535–544, 2010.
- Z. Han, E. Forsberg, and S. He, “Surface Plasmon Bragg Gratings Formed in Metal-Insulator-Metal Waveguides,”IEEE Photonics Technology Letters, vol. 19, no. 2, pp. 91–93, Jan. 15, 2007.
- B. E. A. Saleh and M. C. Teich,Fundamentals of Photonics, John Wiley & Sons, Inc.
- P. B. Johnson and R. W. Christy, “Optical constants of the noble metals,” Phys. Rev. B, vol. 6, no. 12, pp. 4370–4379, Dec. 15, 1972.
- Y. R. Shen,The Principles of Nonlinear Optics, John Wiley & Sons, Inc.



评论 (13)
兰 赵
2022-07-28您好,我用MZ那个案例类似的方式对3D的LN波导进行加电场仿真,采用静电模块后加电压无效果的原因可能是什么呢?材料各向同性设置是不是有一些问题?
Qihang Lin
2022-08-03 COMSOL 员工从描述无法看出来原因,建议您直接将模型上传到技术支持检查://www.denkrieger.com/support
德霄 房
2024-01-07你好,为什么高斯光束的二次谐波生成,电磁波都靠近上边界呢?
Min Yuan
2024-01-09 COMSOL 员工您好,高斯光束的激励表达式中,exp(-y^2/w(x)^2)项定义了光束光轴为y=0,因此光束中心在上边界。
墨飞
2024-01-31您好,这个等离子体波导滤波器的案例怎么才能下载?
hao huang
2024-02-01 COMSOL 员工您好,该案例暂时无法下载,请联系您的销售代表或发送电子邮件至support@comsol.com,获取模型文件。
德霄 房
2024-03-05您好,请问高斯光束的二次谐波生成模型中,在最高峰右边第一个小峰代表二次谐波的生成信号,第二个小峰代表的是几次谐波的生成信号?以及探针图中的纵轴傅里叶系数代表什么样的物理意义?
Min Yuan
2024-03-06 COMSOL 员工您好,一定频率的光与非线性材料相互作用产生二次谐波过程中,也会存在差频、和频效应,第二个小锋可以认为是基频与倍频信号和频产生的三次谐波信号。对于纵轴傅里叶系数,是数学分析中的一个概念,当对瞬态信号进行傅里叶变换,可以展开为不同频率信号的线性组合,那么每个展开项的系数称为傅里叶系数。
德霄 房
2024-03-11那高斯光束的二次谐波案例中纵轴峰值的大小能否代表相应频率在某方向上的振幅呢?考虑多个方向的偏振高斯光束的定义式如果应用在其他方向上应该如何改写?如果改为特定的非线性晶体材料可以直接从材料库中选择吗?
Min Yuan
2024-03-12 COMSOL 员工系数用于表示各频率信号的占比,物理上,纵轴的峰值可以理解为该频率信号的振幅。如果您描述的是改变偏振为不同的方向,您可以参考案例://www.denkrieger.com/model/scatterer-on-substrate-14699 。如果材料库中的材料参数与您预期一致,当然是可以的,但如果已知材料的材料参数,建议直接自定义相关属性。
思聪 习
2024-06-19您好,如果想仿真周期性极化晶体的非线性效应,可以通过在瞬态方法中的剩余电位移添加方波调制或在频域方法中对极化添加方波调制来实现吗,我尝试了一下以上两种,似乎结果都不正确。由于我没有更改案例的默认材料,会不会和这个原因有关?
Qingbin Yuan
2024-06-20 COMSOL 员工1.您这里提到的两种模拟非线性过程的方法都是可以的。其中,对于周期性极化,可能瞬态的方法会更合适一些。
2.不知道您说的“结果不正确”具体指的是如何不正确?可否具体说明?
3.材料属性对结果的影响肯定是至关重要的。尤其是非线性系数,直接影响材料对外部电场变化的响应。
思聪 习
2024-06-24感谢您的回复!
关于第一点,在瞬态方法中,我使用方波调制非线性系数似乎只能对二阶以上的极化实现调制,并不能将材料整体的极化反转过来。
关于第二点,在瞬态的仿真中,添加方波调制后,完全观察不到非线性效应。频域的仿真中,添加方波调制极化之后,并不能实现预期的准相位匹配的效果。