1669 年一个晴朗的夜晚,Erasmus Bartholinus 教授正在把玩一块放在长凳上的冰岛方解石晶体。他突然发现,当方解石覆盖长凳上的文字时,这些文字看起来像一个双重图像。他观察到的这个光学现象称为双折射,是由一束光从晶体中射出时分裂成两个平行光束引起的。我们将在本篇博客中演示这种效应的建模方法。
了解各向异性材料
Erasmus Bartholinus观察到的穿过晶体的直射光束称为寻常光线,另一种在穿过晶体时发生弯曲的光束,是一种非常光线。从检测有害气体到光子集成电路光束分裂的应用中都广泛存在着各向异性材料,例如上述方解石和长凳实验中的晶体。
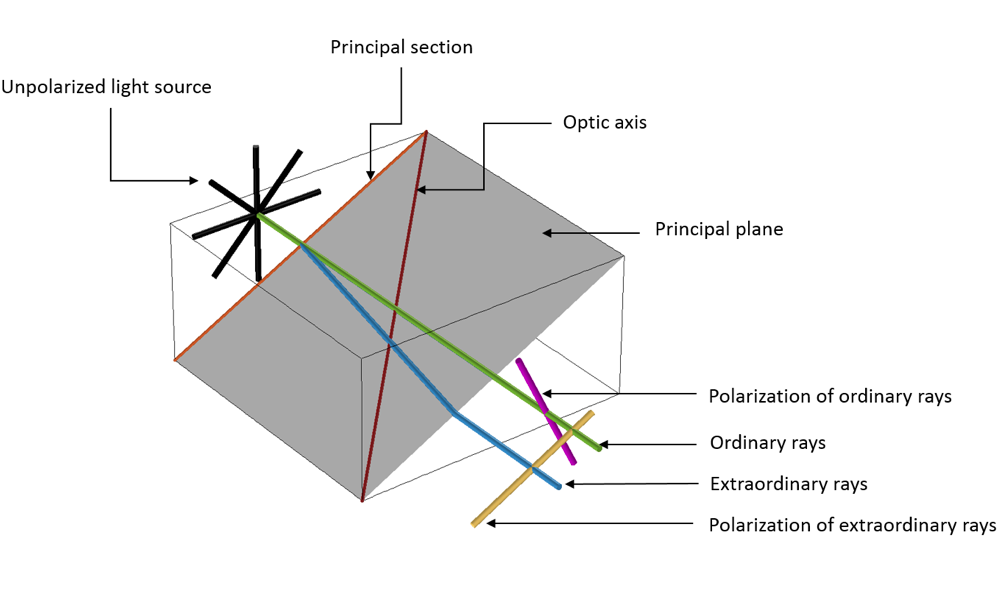
穿过各向异性晶体的寻常光线和非常光线。
在物理环境中,当非偏振电磁波束通过各向异性电介质材料传播时,将使得电介质发生极化,产生称为电偶极子的电荷分布。这种现象导致各向异性电介质材料内出现感应场,其中两种波的折射率不同(寻常波和非常波)。
寻常波在垂直于主平面的方向发生偏振,非常波在平行于主平面的方向发生偏振,其中光轴和晶体中的两个传播方向位于主平面。由于这种特性,波以不同的速度和轨迹传播。
在硅波导中引入各向异性
在之前的一篇博客文章中,我们讨论了由于与 CMOS 制造技术的兼容性,硅及其衍生物二氧化硅如何在光子集成芯片中广泛使用。具有各向同性特性的硅材料用于开发光子集成芯片的原型。然而,由于具有分裂光束和基于偏振的光学效应等光学特性,各向异性材料逐渐显露头角。
在制造波导时的退火过程中,硅光子学中的各向异性偶有显现。由于应力光学效应,纤芯与包层之间的热膨胀差异会导致几何结构失配,从而导致模式分裂和脉冲展宽等效应。各向异性也可以通过改变二氧化硅的孔隙率而有意引入,这样,研究人员能够使用包括二氧化硅(n~1.44)和空气(n~1)在内的一系列有效折射率,从而能够实现非常灵敏的光学传感器应用。
光学传播模式
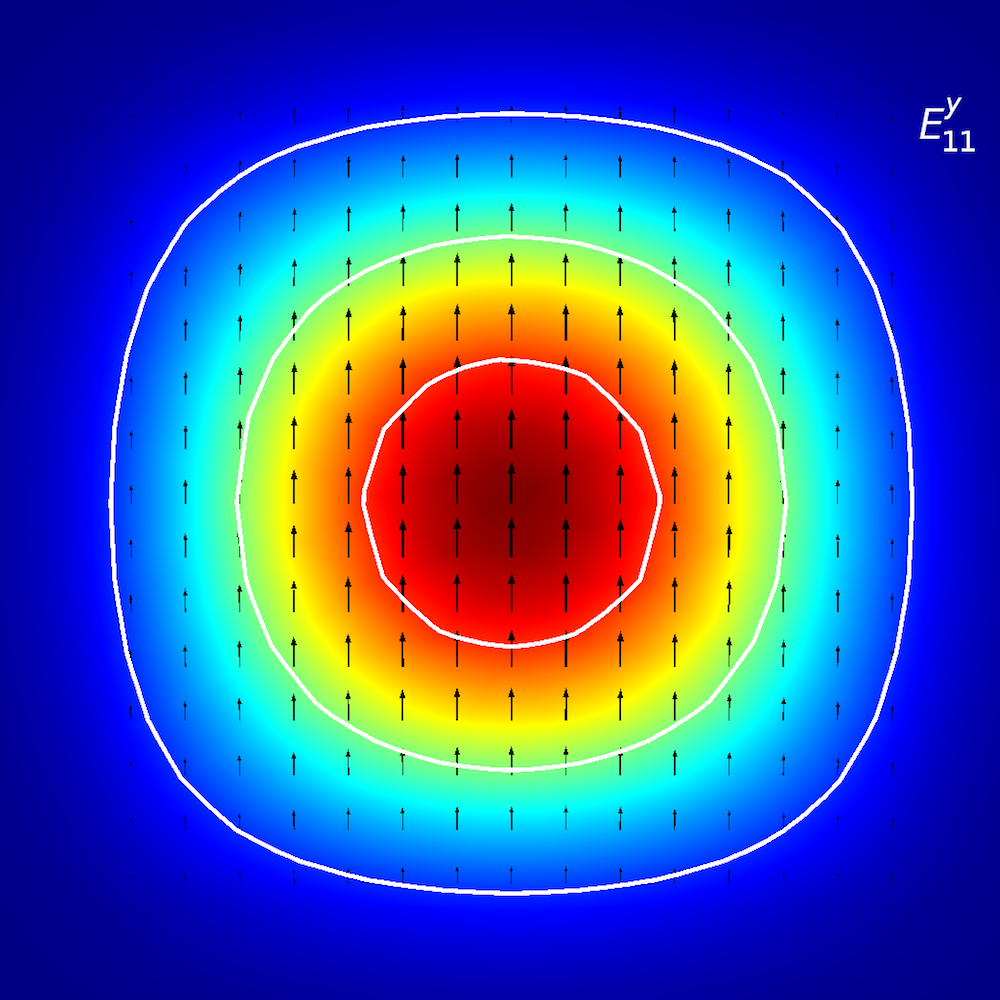
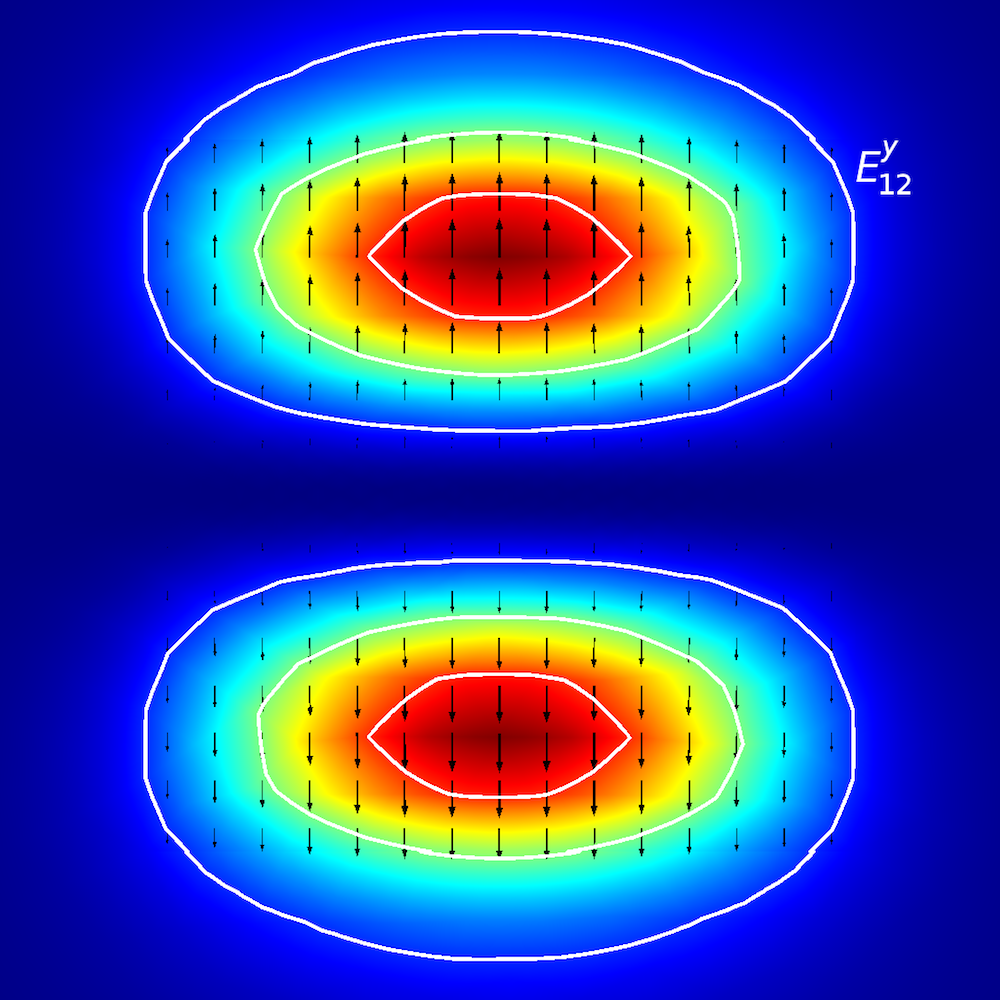
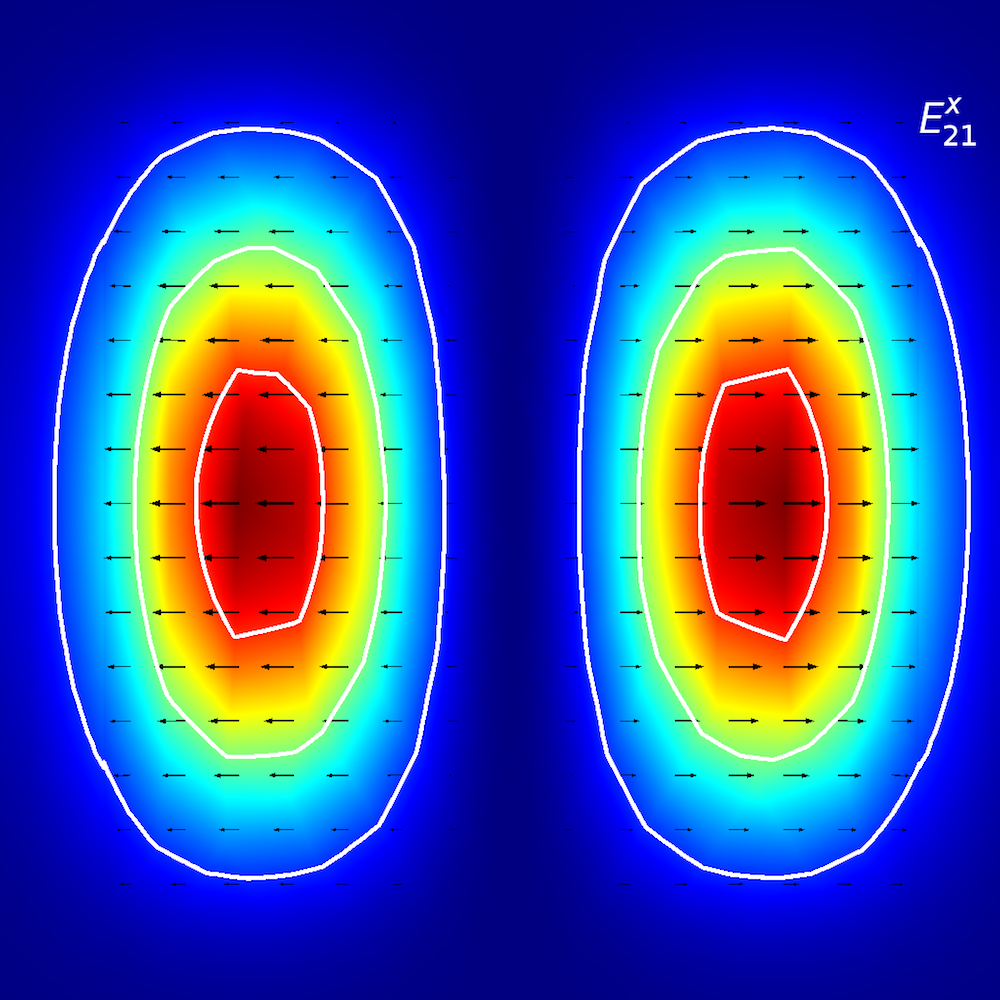
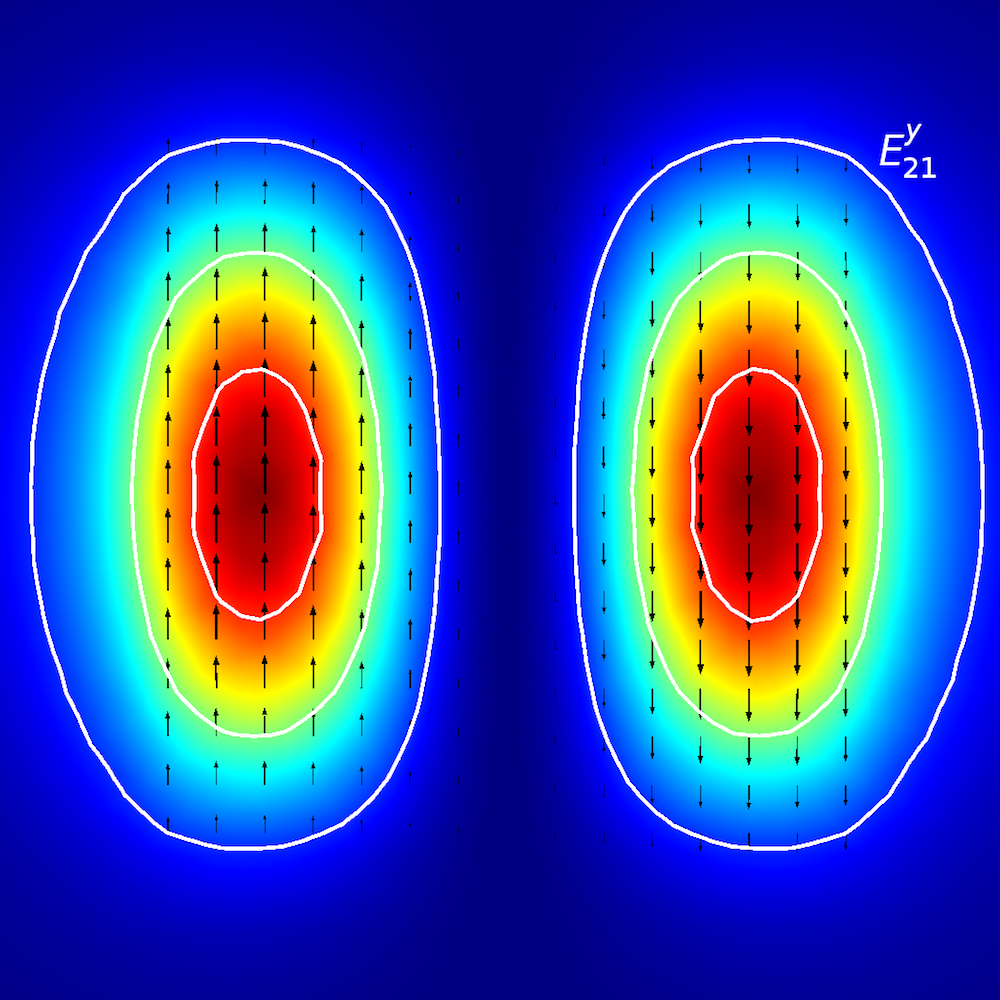
为了对各向异性介质进行定性分析,研究人员研究了光能如何在平面波导内传播(也称为传播模式)。在平面波导中,我们使用E^{x}_{p,q}和E^{y}_{p,q}(参考文献 2)定义模式,其中x和y表示偏振方向,p和q表示x和y坐标中的最大值。
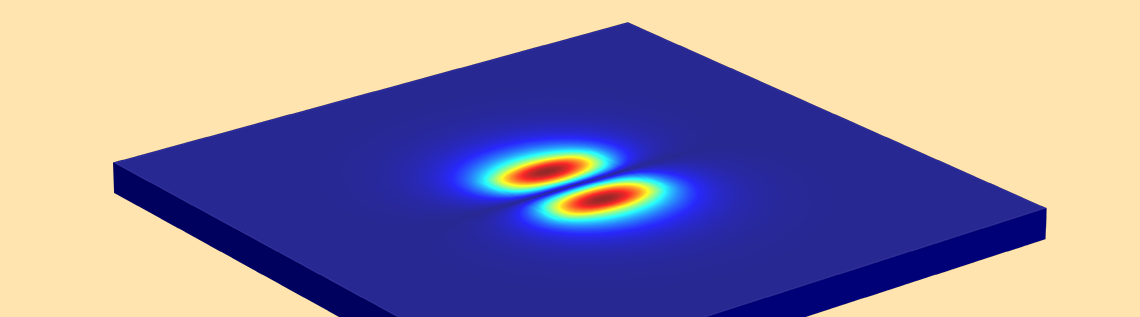
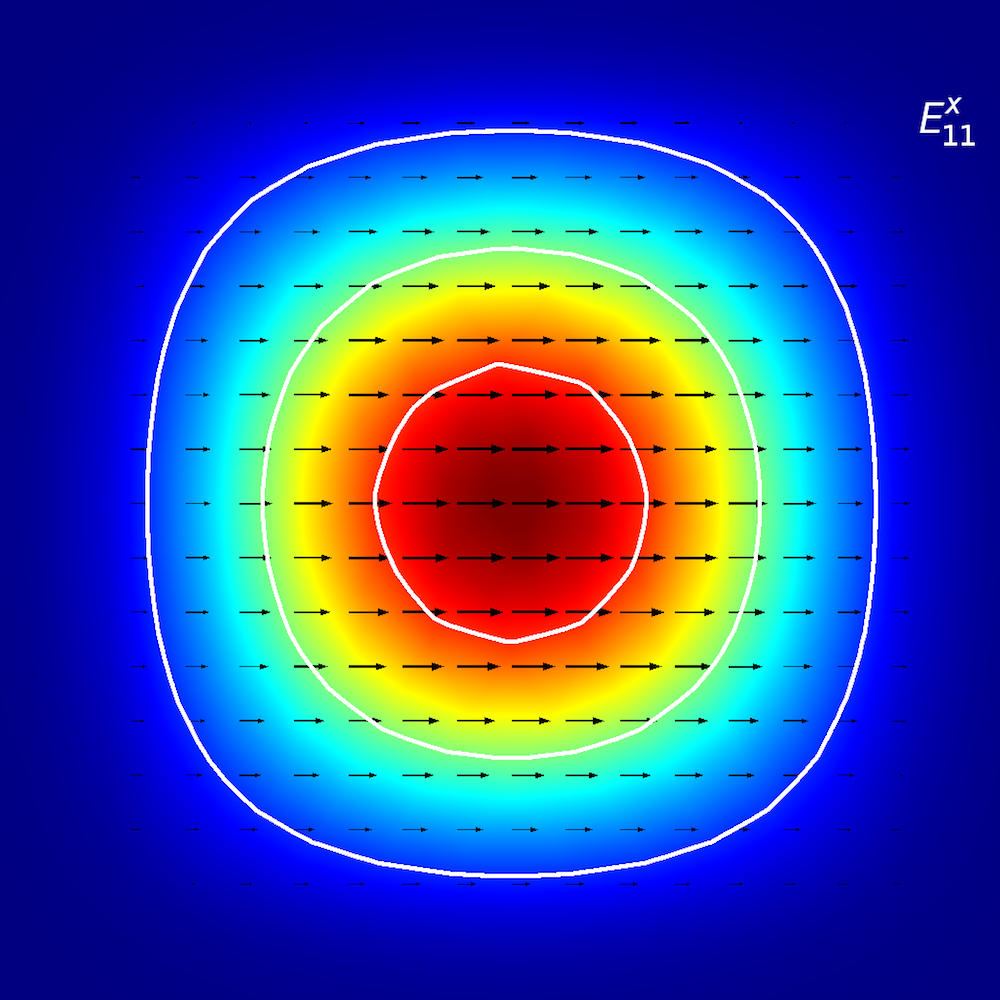
想象一下:你走在一幅E^{x}_{2,1}“风景画”上(如下图所示),“风”(偏振)沿 ±x 方向吹过。从-x到 +x方向行进时,你会遇到两个不同的峰。当你从-y 方向朝+y方向移动时,可以同时观察到两个峰值。
平面波导的模式分析。顶行,从左到右:E^{x}_{1,1}和E^{y}_{1,1}。中间行,从左到右:E^{x}_{1,2}和E^{y}_{1,2}。底行,从左到右:E^{x}_{2,1}
和E^{y}_{2,1}。箭头图表示电场; 云图和表面图表示面外功率流(红色表示高幅值,蓝色表示低幅值)。
在 COMSOL Multiphysics® 软件中分析各向异性结构
在使用激光源通过波导发射光束之前,了解哪些光学模式可以在波导的特定芯/包层尺寸内持续存在是非常重要的。使用全矢量有限元工具(例如COMSOL Multiphysics® 软件)进行模式分析,有助于分别定性和定量地分析光学模式和色散曲线。
引入对角各向异性
对任何各向同性材料进行模态分析都需要定义单个复数值,而对于各向异性材料的情况,需要采用全张量相对介电常数方法。介电常数本质上是电场与材料属性的关系。这里,张量指的是一个 3 x 3 矩阵,它同时具有对角线(\epsilonxx,\epsilonyy,\epsilonzz)和非对角线(\epsilonxy,\epsilonxz,\epsilonyx,\epsilonyz,\epsilonzx,\epsilonzy)项,如下所示。
{bmatrix}
\epsilon_{xx}&\epsilon _{xy}&\epsilon _{xz}\\
\epsilon _{yx}&\epsilon _{yy}&\epsilon _{yz}\\
\epsilon _{zx}&\epsilon _{zy}&\epsilon _{zz}
\end{bmatrix}
但是,对于所有材料来说,你可以找到一个坐标系,在这个坐标系中,介电常数张量中只有非零对角线元素,而非对角线元素都为零。这个旋转坐标系中的三个坐标轴是材料的主轴,相应地,介电常数张量中对角线元素的三个值被称为材料的主介电常数。
各向异性晶体主要有两种:单轴晶体和双轴晶体。在选择适当坐标系(其中只有介电常数张量的对角线元素是非零的)的情况下,就光学属性而言,单轴晶体仅考虑对角线项,即\epsilonxx=\epsilonyy= (no)2,\epsilonzz= (ne)2,其中no和ne分别是寻常折射率和非常折射率。然而,当\epsilon_
{xx}\neq \epsilon_{yy} \neq \epsilon_{zz}时,它被称为双轴晶体。
为了将这个论点纳入建模的角度,我们可以扩展这篇关于硅光子学设计的博客文章中的隐埋肋波导示例。我们可以对方形芯和包层长度分别为 4 um 和 20 um 的波导的二维横截面(如下所示)执行模式分析。所有情况下的工作波长都被认为是 1.55 [um]。

三维隐埋肋光波导示意图,其中对入口二维横截面执行模式分析。强度图和箭头图分别代表电场的模式和极化。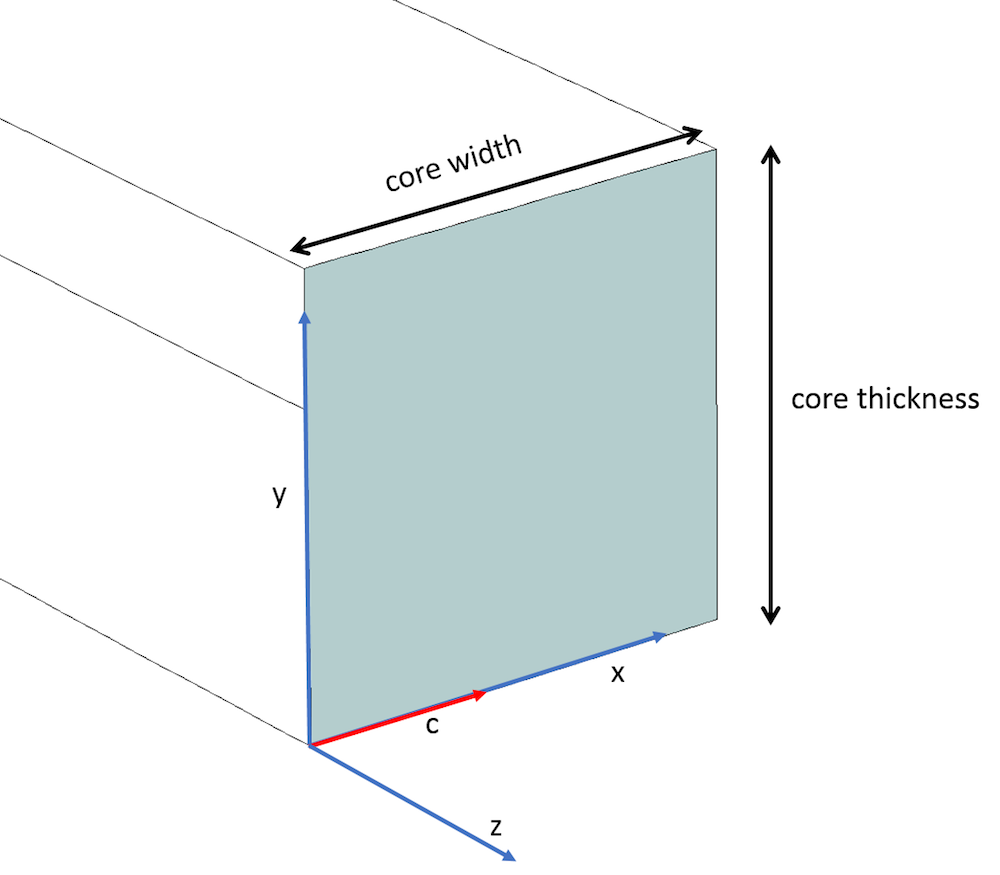
标出沿x轴的光轴(红色)和主轴(蓝色)的肋波导芯。
在传统的单轴材料情况下,我们假设光轴(即c轴)沿着主x轴(如上所示),并将对角相对介电常数\epsilonyy和\epsilonzz项(与c轴正交)视为寻常折射率的平方(~1.51992~2.31)。沿c轴的\epsilonxx分量元素被认为是非常折射率的平方(~1.47992~2.19)(参见参考文献 3)。此外,非对角线项被认为是零(如下所示),包层具有各向同性的相对介电常数(~1.43182)。导出的光学模式是上面所示的 6 种模式。请注意折射率的差:“nxx–nyy”称为双折射,其中nxx=\sqrt{\epsilon_{xx}},nyy=\sqrt{\epsilon_{yy}}。
\begin{bmatrix}
2.19 & 0 & 0\\
0 & 2.31 & 0\\
0 & 0 & 2.31
\end{bmatrix}
具有对角线元素的相对介电常数张量。
色散曲线
通过计算光学模式,我们可以直观地理解光波导的特性。此外,对色散曲线进行定量分析也相当方便。通常色散曲线表示有效折射率相对于波导长度或工作频率的变化。
对角各向异性
在 0.5 um 到 4 um 范围内对波导长度进行参数化扫描的同时执行模式分析,以推导出各向异性芯的色散曲线,如下图所示。我们假设为前面提到的情况,芯具有对角各向异性项(即\epsilonxx= 2.19,\epsilonyy=\epsilonzz= 2.31,所有对角线元素都为零)。将结果与 Koshiba 等人的结果(参考文献 3)进行比较。
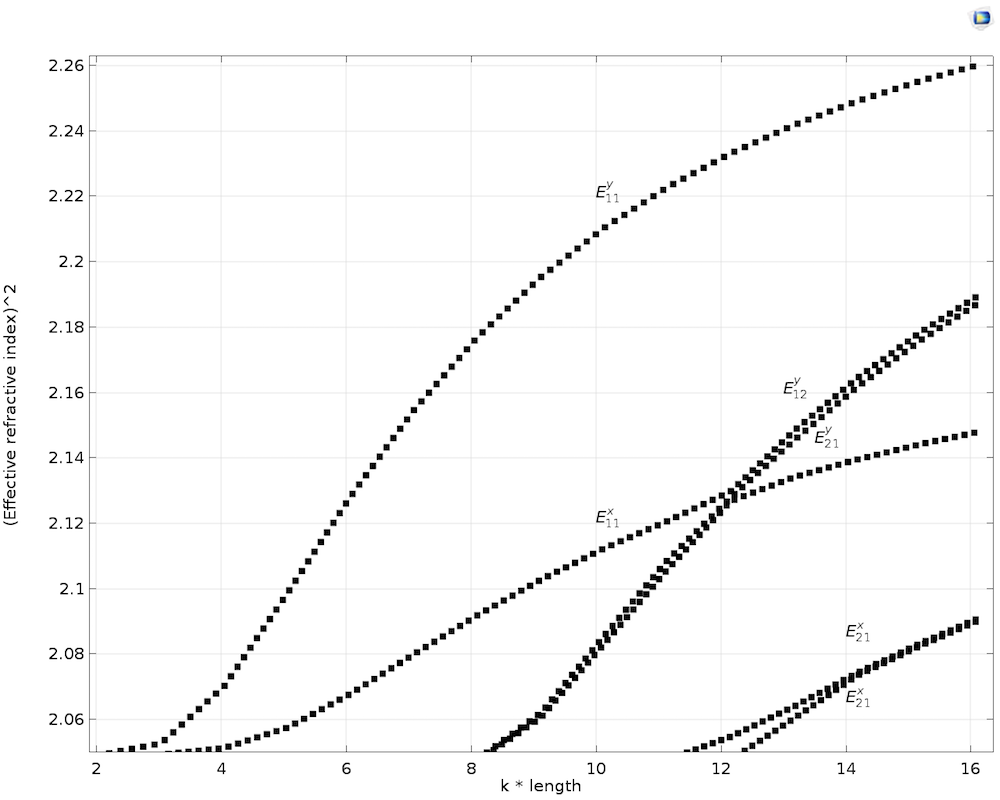
横向各向异性芯的色散曲线。
非对角横向各向异性(XY 平面)
当光轴(即,c轴)位于 XY 平面并与x轴成\theta角时,对角线分量\epsilonxx,\epsilonyy,\epsilonzz和非对角线分量\epsilonxyand\epsilonyz非零,而其余分量为零。可以通过使用如下所示的旋转矩阵 [R] 来计算全相对介电常数张量,其中旋转矩阵 [R] 专门用于在 XY 平面中旋转c轴。由于c轴沿着主x轴,因此\epsilonxx是非常折射率的平方(~2.19),而\epsilonyy和\epsilonzz是寻常折射率的平方(~2.31)。非对角线元素\epsilonxy和\epsilonyz是根据矩阵的乘法计算导出的,如下所述。
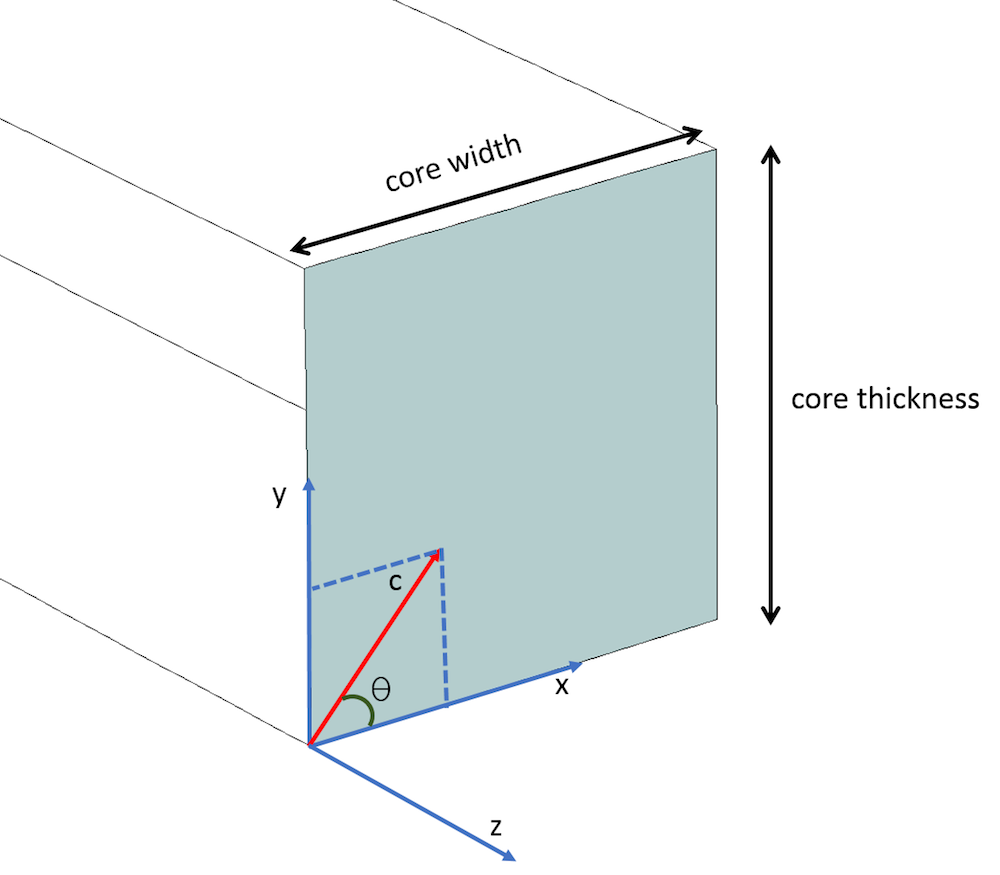
c 轴位于 XY 平面,与 x 轴成\theta角。
\begin{bmatrix}
cos(\theta) & -sin(\theta) & 0 \\
sin(\theta) & cos(\theta) & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx}
& 0 & 0 \\
0 & \epsilon_{yy} & 0 \\
0 & 0 & \epsilon_{zz}
\end{bmatrix}
\begin{bmatrix}
cos(\theta) & sin(\theta) & 0 \\
-sin(\theta) & cos(\theta) & 0\\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
(\epsilon_{xx}) cos^2(\theta) + (\epsilon_{yy}
) sin^2(\theta) & (\epsilon_{xx}) sin(\theta) cos(\theta)-(\epsilon_{yy}) sin(\theta) cos(\theta) & 0 \\
(\epsilon_{xx}
) sin(\theta)cos(\theta)-(\epsilon_{yy})sin(\theta)cos(\theta) & (\epsilon_{yy}
) cos^2(\theta) + (\epsilon_{xx}) sin^2(\theta) & 0\\
0 & 0 & \epsilon_{zz}
\end{bmatrix}
相对介电常数张量ε与旋转矩阵一起处理,在 XY 平面内将c轴旋转角度\theta。
最后,对具有非对角各向异性芯和各向同性包层的波导进行模式分析,其中光轴与主x轴成 0 度、15 度、30 度和 45 度的角,如下所示。从图中我们可以观察到面内磁场的方向根据光轴角度的变化而变化。也可以通过在 0.5 um 到 4 um 范围内对芯和包层的长度执行参数化扫描,同时将角度\theta视为 45°,绘制色散曲线。如上所述,结果往往类似于对角各向异性的色散曲线。
θ= 0°(左上)、θ= 15°(右上)、θ= 30°(左下)、θ= 45°(右下)时的模式分析,包括非对角项 。图示表示不同旋转角度下芯内的磁场线。
非对角纵向各向异性(YZ 平面)
最后,当假设为光轴(即,c轴)位于 YZ 平面并与y轴成\phi角的纵向各向异性时,对角线分量\epsilonxx、\epsilonyy、\epsilonzz和非对角线分量\epsilonyz、\epsilonzy非零,而其余分量为零。可以通过使用如下所示的旋转矩阵 [R] 来计算相对介电常数张量,其中旋转矩阵 [R] 专门用于在 YZ 平面中旋转c轴。由于c轴沿着主y轴,因此\epsilonyy是非常折射率的平方(~2.19),而\epsilonxx、\epsilonzz是寻常折射率的平方(~2.31)。非对角线元素\epsilonyz和\epsilonzy是根据矩阵的乘法计算导出的,如下所述。
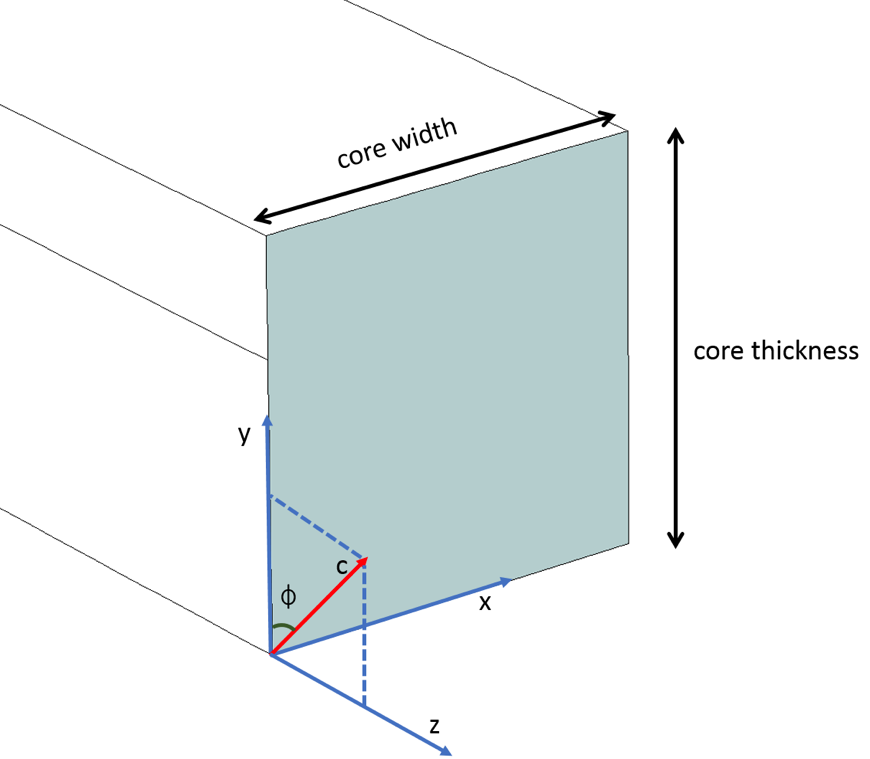
c轴位于 YZ 平面,与 x轴成\phi角。
\begin{bmatrix}
1 & 0 & 0 \\
0 & cos(\phi) & -sin(\phi)\\
0 & sin(\phi) & cos(\phi)
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx}
& 0 & 0 \\
0 & \epsilon_{yy} & 0 \\
0 & 0 & \epsilon_{zz}
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & cos(\phi) & sin(\phi)\\
0 & -sin(\phi) & cos(\phi)
\end{bmatrix}
\begin{bmatrix}
\epsilon_{xx} & 0 & 0 \\
0 & (\epsilon_{yy}
) cos^2(\phi) + (\epsilon_{zz}) sin^2(\phi) & (\epsilon_{yy})sin(\phi)cos(\phi)-(\epsilon_{zz}
) sin(\phi)cos(\phi)\\
0 & (\epsilon_{yy})sin(\phi)cos(\phi)-(\epsilon_{zz}) sin(\phi)cos(\phi) & (\epsilon_{zz}) cos^2(\phi) + (\epsilon_{yy}
) sin^2(\phi)
\end{bmatrix}
相对介电常数张量ε通过旋转矩阵处理,表示在 YZ 平面内旋转角度\phi。
然后通过在 0.5 um 到 4 um 范围内对芯和包层的长度执行参数化扫描来执行模式分析,以导出纵向各向异性芯的色散曲线,如下图所示。在本例中,\phi= 45°(即,c轴位于 YZ 平面,与y轴成 45° 角)(参考文献 3)。
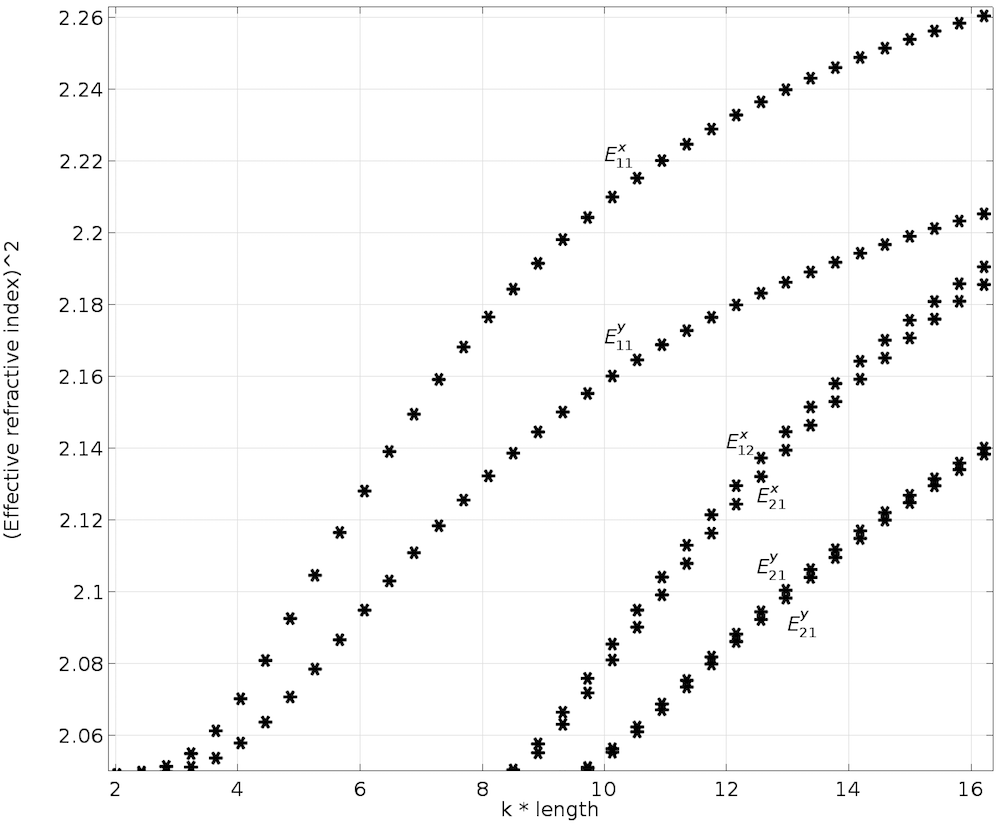
纵向各向异性芯的色散曲线。
关于各向异性材料建模的最后思考
在本篇博客文章中,我们使用 COMSOL Multiphysics 中的模式分析对各向异性光波导进行了定性分析(传播模式)和定量分析(色散曲线),其中考虑了对角各向异性以及非对角横向和纵向各向异性来推导它们的色散关系。通过执行这些类型的分析,我们在优化材料和几何参数时更加灵活,这有助于我们深入、直观地了解各向异性材料的物理特性。
阶跃折射率光纤这个简单的教程模型可以帮助你入门,该模型包含对三维光纤二维横截面的模式分析。
后续操作
如需尝试操作这些模型,请单击下面的按钮进入“案例下载”页面,只要你拥有 COMSOL Access 帐户和有效的软件许可证,即可从中下载相关的 MPH 文件。
硅光子学系列博客文章更新列表
- 第 1 部分:硅光子学:硅波导的设计和原型制作
参考文献
- E. Hecht,Optics, Pearson.
- E.A.J. Marcatili, “Dielectric rectangular waveguide and directional coupler for integrated optics”,Bell Syst. Tech. J., vol. 48, pp. 2071–2102, 1969.
- M. Koshiba, K. Hayata, and M. Suzuki, “Finite-element solution of anisotropic waveguides with arbitrary tensor permittivity,”Journal of Lightwave Technology, vol. 4, no. 2, pp. 121–126, 1986.








评论 (0)