如何模拟金属-硅-氧化物电容器的界面陷阱效应

陷阱在实际的半导体器件中无处不在。在对这些器件进行建模时，COMSOL 软件中的陷阱辅助表面复合边界条件增加了通过表面或界面陷阱进行的充电和载流子捕获/释放的影响。本文，我们研究了一个金属-硅-氧化物电容器 (MOSCAP) 教程模型，用于演示如何在 COMSOL Multiphysics^®软件的附加产品——半导体模块中使用这项功能。

关于陷阱辅助表面复合边界条件

陷阱辅助表面复合边界条件增加了表面复合率和与表面陷阱相关的表面电荷密度，用于绝缘、薄绝缘栅、绝缘体界面和金属接触（理想肖特基型）边界条件。这项功能取代并扩展了 COMSOL^®软件 5.4 之前版本中的显式陷阱复选框功能。Shockley-Read-Hall 模型和显式陷阱分布选项都可以使用。

模拟金属-硅-氧化物电容器

金属-硅-氧化物结构是许多硅平面器件的基本要素。因此，我们在半导体模块的案例库中包含了一些金属-硅-氧化物电容器教程模型。在这里，我们使用一维 MOSCAP 界面陷阱模型来展示陷阱辅助表面复合特征。

顾名思义，金属-硅-氧化物电容器模型是一个简单的一维 MOSCAP 模型，包括界面陷阱的影响。该模型是基于 E.H. Nicollian 和 A. Goetzberger 的论文（参考文献 1）的图 14 中描述的实验装置（n 型样品）建立的。

实验样品是使用在低电阻率衬底上生长的 10 um厚的外延层制备的，用于最大限度地减少体串联电阻的影响。在模型中，假设外延层厚度相同(10 um)，衬底厚度为 2 um，并假设体串联电阻可以忽略不计。假设氧化物厚度为 60 nm，位于 50-70 nm 实验范围的中间。栅的直径为 3.8×10^-2cm，如论文中的图题所示。

假设电子迁移率恒定为 1450 cm²/V/s。然后分别由电阻率的实验值 0.75 和 0.005 ohm-cm 计算外延层和衬底中的 n 掺杂浓度。

假定氧化物介电常数为 3.9，然后根据介电常数、厚度和栅极直径计算氧化物电容。

如论文所给出的，固定氧化物电荷密度为 9×10¹¹cm^-2。除陷阱电荷外，该值还包含在模型中。

假定陷阱能量分布为矩形，范围为0.2 eV，以中间间隙为中心。假定矩形的高度为2×10¹¹cm^-2eV^-1，如论文中的图15 示。对于捕获过程，假定热速度为 10⁷cm/s，电子和空穴的横截面分别为 1×10^-15cm²和 2.2×10^-16cm²，如图15 的同一页所示。

假设栅极的金属功函数为4.5 eV。

设置陷阱辅助表面复合边界条件

默认情况下，边界条件的捕获模型是Shockley-Read-Hall 模型。对于本教程，它有一个矩形陷阱能量分布，我们改为选择显式陷阱分布选项。然后，在陷阱部分，选择指定连续和/或离散能级数选项。下面的屏幕截图显示了这些设置。

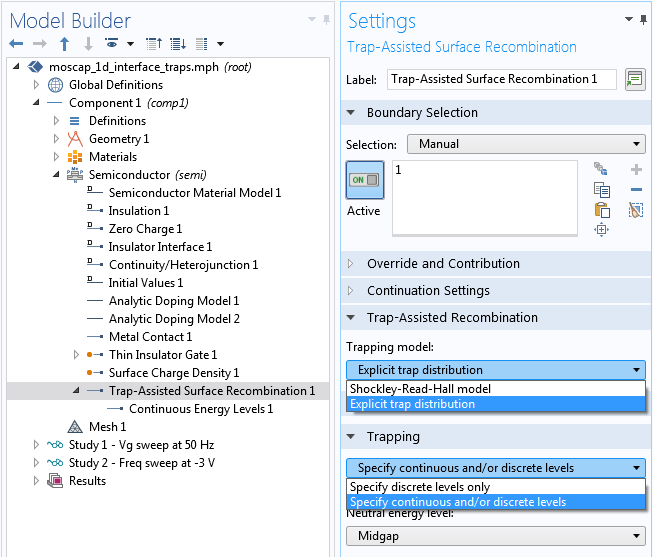
设置陷阱模型和陷阱能级选项。

显式陷阱分布选项需要一个或多个子节点来指定陷阱能级的分布，以使边界条件生效。在这里，我们添加了连续能级 1子节点。

使用软件的额外维度功能，连续陷阱能量分布由沿能量轴的多个离散水平近似。通过将离散化范围缩小到与矩形分布相同，我们可以更有效地利用额外维度，如下面的屏幕截图所示；例如，将连续能量离散化，最小能量(E_t,min输入字段)semi.tasr1.ctb1.Et0-Ew0/2。

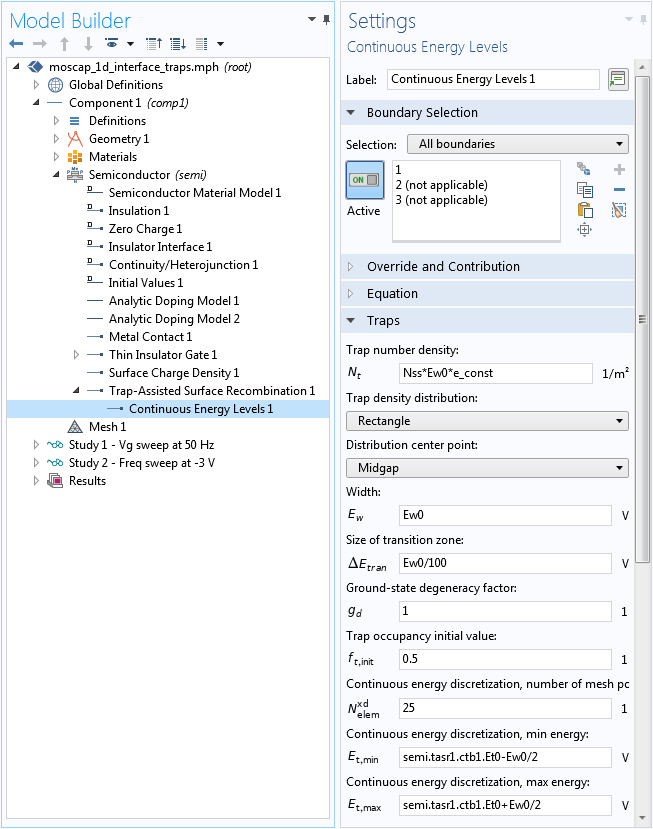
建立连续的陷阱能量分布。

检查半导体仿真结果

论文中描述的实验测量了样本的小信号响应；因此，我们还对模型进行了小信号分析。下图显示了计算出的终端电容和等效并联电导作为栅极电压的函数，用于和参考文献1中的图23 进行比较。曲线显示了与实验数据在定性上具有相似数量级的行为（注意等效并联电导的峰值和终端电容的扭动）。

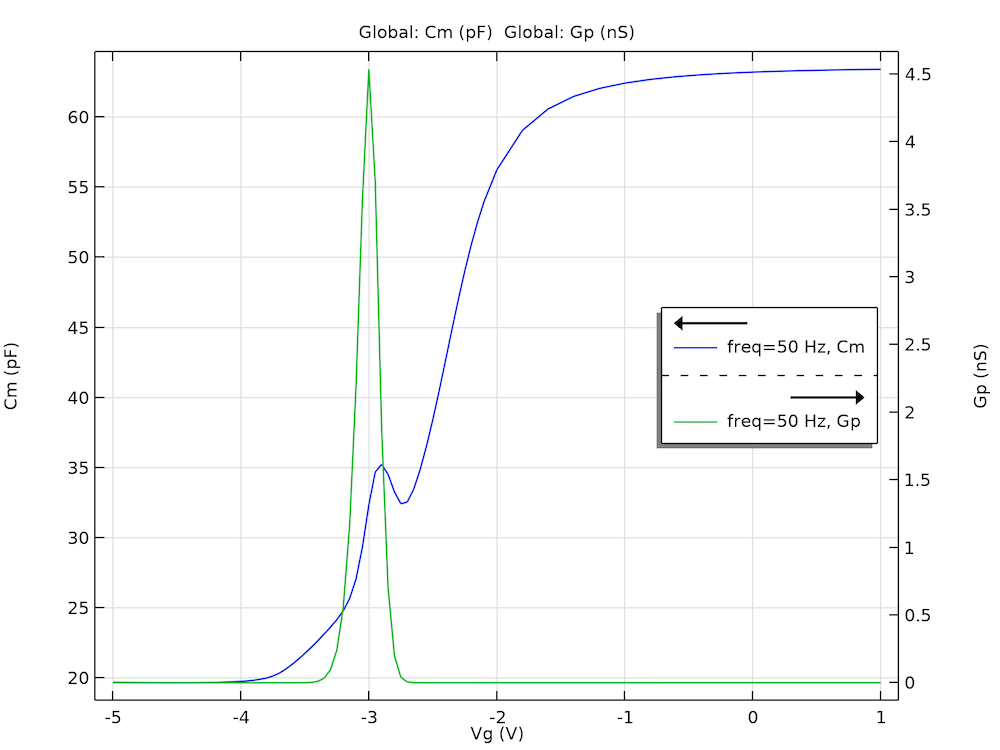
计算的终端电容(Cm)和等效并联电导(Gp)与栅极电压(Vg)的函数关系，显示出与本文报道的实验数据相同的定性行为和类似的数量级。

下图显示了计算的终端电容和等效并联电导与小信号频率的函数关系。等效并联电导的定性行为与论文中的图 25 相比良好(该图不包括终端电容)。

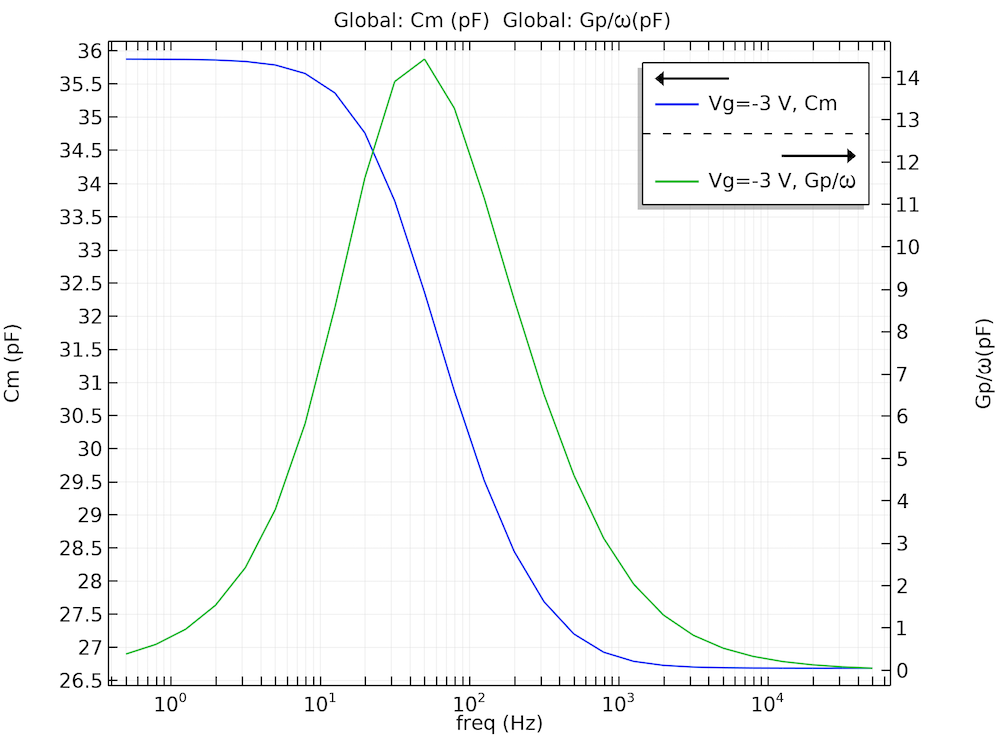
计算的终端电容(Cm)和等效并联电导(Gp)与小信号频率的函数关系。

深入了解界面陷阱的物理特性

仿真的好处之一是通过研究实验无法访问的数值来帮助我们更好地理解系统。在这个模型中，我们可以沿着能量轴绘制模拟的陷阱占有率，以深入了解测量的电容和电导曲线的行为，如上图所示。

如上所述，物理场接口使用额外维度分量将能量轴添加到模型中。为了沿着能量轴绘制任何数量，我们首先创建一个数据集，指向定义数量的额外维度分量。这可以很容易的通过复制感兴趣的数据集，然后在分量下拉菜单中选择额外维度选项来完成，如下面的屏幕截图所示。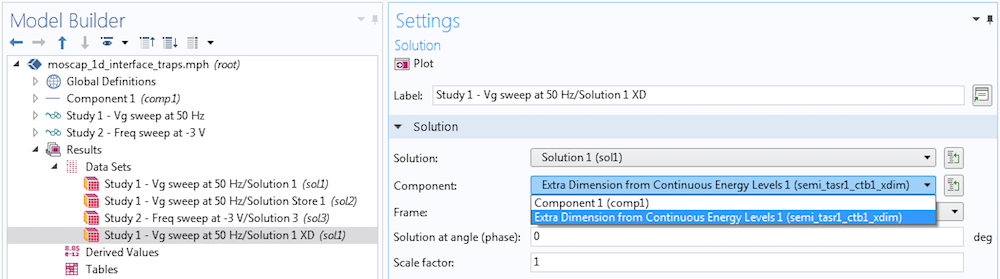

创建数据集以沿能量轴绘制数量。

除了数据集，要绘制的表达式需要使用atxd算子，这有助于评估额外维度（沿能量轴）中的变量。例如，下面屏幕截图显示了折线图的 y轴数据和 x轴数据的表达式。atxd0算子与”0“一起使用，因为能量轴（额外维度）是在边界条件中定义的，在一维模型中其维度为 0。算子的第一个参数是0[um]，因为边界条件被施加在位于模型几何结构 0 um 处的边界。

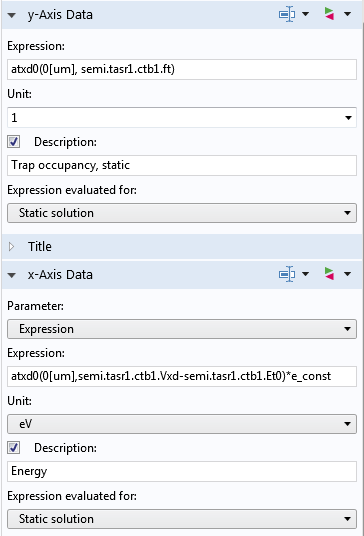
折线图的 y 轴和 x 轴数据的表达式。

下图显示了两种情况下沿能量轴的稳态（偏置点）陷阱占有率：

1. 栅极电压= 1 V（累积）
2. 栅极电压= -3 V（平衡并联电导峰值）

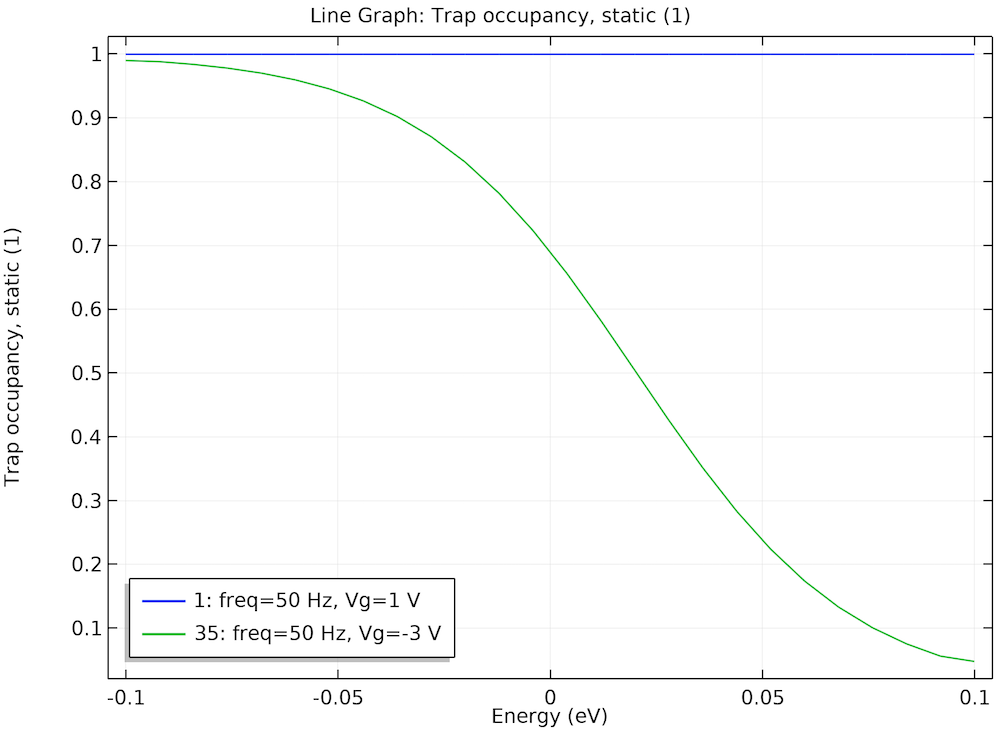
两个偏置点处的稳态陷阱占有率可以深入了解计算的终端电容和等效平行电导曲线的行为。

由于费米能级远高于陷阱能级，我们看到在 1 V 的栅极电压下，陷阱被完全占据（蓝色曲线）。在这种情况下，我们不会期望陷阱对小信号响应有任何重大贡献。然而，在 -3 V 的栅极电压下，费米能级穿过陷阱能量分布的中间，因此许多陷阱能级被部分占据（绿色曲线）。在这种情况下，我们预计陷阱会对小信号响应做出重大贡献。这确实与前面的图中看到的等效并联电导峰值和 -3 V 处终端电容曲线的明显摆动一致。

下图显示了陷阱占据沿能量轴的小信号响应，并比较了相同的两种情况：栅极电压= 1 V（累积）和栅极电压= -3 V（平衡并联电导峰值）。由于小信号响应是复值，因此我们绘制了实部（实线）和虚部（虚线）。

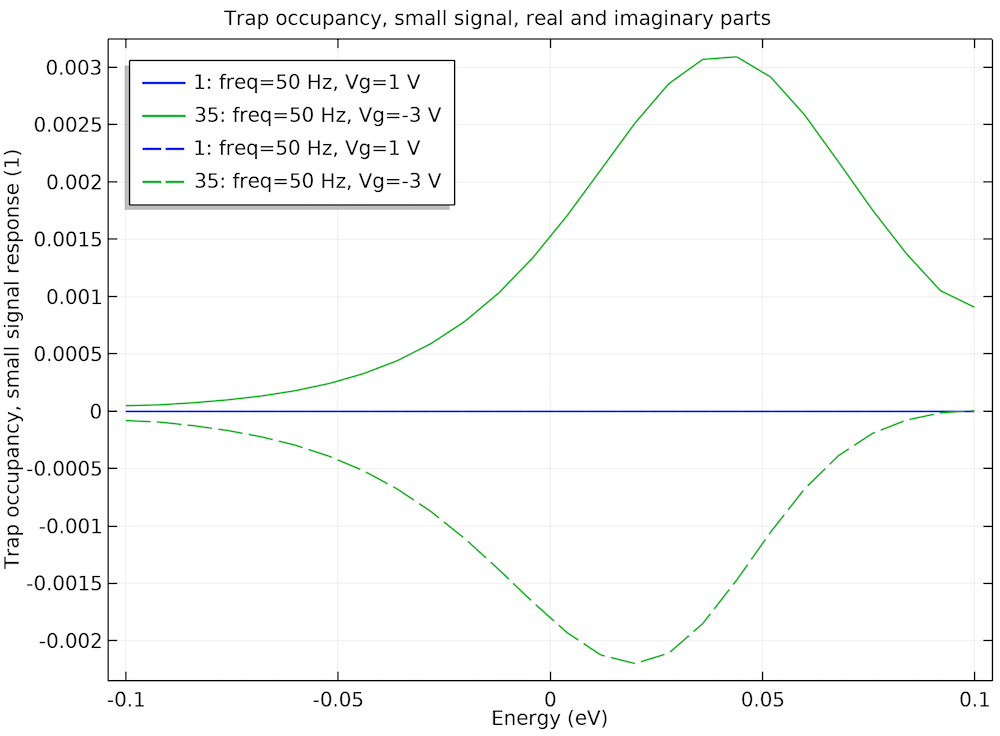
在相同的两个偏置点处陷阱占用的小信号响应进一步证实了之前的观察。实曲线：实部；虚线：虚部。

一方面，我们看到在 1 V 的栅极电压下，陷阱占用的小信号响应的实部和虚部都非常小（蓝色曲线）。另一方面，在 -3 V 的栅极电压下，陷阱占用的小信号响应的实部和虚部都很重要（绿色曲线）。所有这些都进一步证实了上面给出的物理论证。

下一步

在这篇博文中，我们展示了陷阱辅助表面复合边界条件为半导体器件模型增加了基本效应，用于重现文献中通过实验数据发现的定性行为。我们还展示了如何在额外维度中绘制变量，例如模型中的能量轴。

想要亲自尝试金属-硅-氧化物电容器的界面陷阱效应教程模型吗？请单击下面的按钮进入 COMSOL 案例库，您可以下载包含分步说明的 PDF 文档和本教程的 MPH 文件。

我们希望这个特征对您有用，也欢迎您与我们分享您是如何将这个特征应用到您的研究中。

参考文献

1. H. Nicollian and A. Goetzberger, “The Si-SiO2 interface – electrical properties as determined by the metal-insulator-silicon conductance technique” The Bell System Technical Journal, vol. 46, issue 6, Jul./Aug. 1967).