如何获取疲劳模型参数

在模拟疲劳时，需要解决两个主要难题。第一个是选择合适的疲劳模型，第二个是获取选定模型的材料数据。在上一篇文章 “我应该选择哪种疲劳模型？“中，我们对第一个问题进行了讨论，并给出了一些解决方法。今天，我们将讨论第二个问题，并介绍如何获取疲劳模型参数。

使用多种不同的模型预测疲劳

疲劳模型是基于物理场假设的，因此被称为唯象模型。不同条件下的疲劳由不同的微观力学原理控制，因此需要建立很多解析和数值关系来包括所有的疲劳类型，而这些疲劳模型又需要专门的材料参数。

众所周知，疲劳测试很昂贵。因为导致疲劳发生的杂质在材料中是随机分布的，所以必须测试许多样本。当用 S-N 曲线将所有的测试结果可视化时，疲劳寿命的差异就可以清楚的呈现出来。

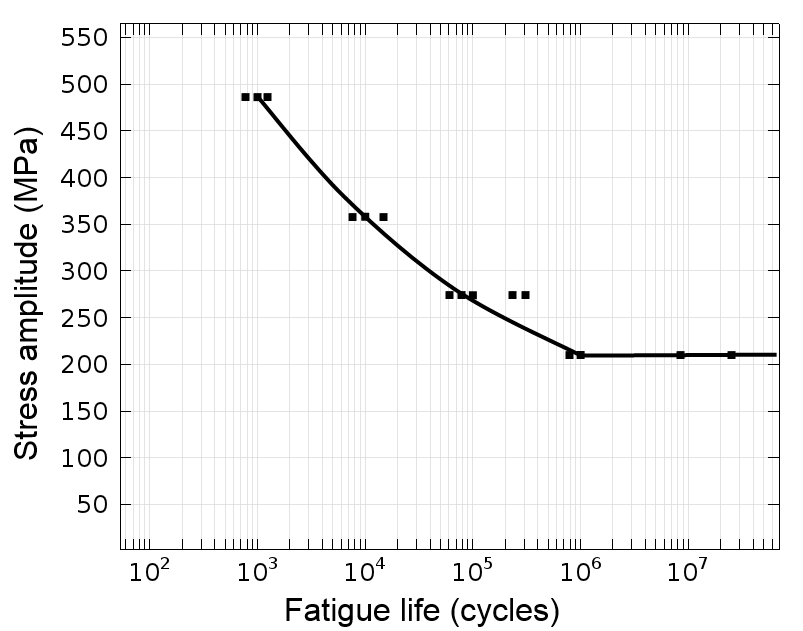
一个 S-N 曲线。黑色方块代表单个疲劳测试。

通过 S-N 曲线获得模型参数的建议

S-N 曲线，也叫 Wöhler 曲线，是最古老的一种疲劳预测方法，所以很有可能材料的数据已经通过这种形式显示出来了。很多时候，这些数据是针对 50% 的失效风险给出的。如果无法获得材料数据，就需要进行测试。

当完成测试后，需要注意统计方面的问题，即在每个载荷水平上，构建 S-N 曲线时需要选择相同的可靠性。这一点很重要，因为 S-N 曲线是以对数尺度表示的，输入的微小差异都会对输出有很大影响。不同可靠性水平的 S-N 曲线需要彼此分开，因此在实际模拟时，应该选择一个合适的水平。对于非关键性结构，50% 的失效率可能是可以接受的。但是，对于关键结构，应该选择一个明显较低的失效率。

当使用不同来源的疲劳数据时，一定要注意确保测试条件和操作条件相同。

运行考虑平均应力的疲劳测试的建议

疲劳测试的另一个方面是考虑对疲劳寿命有很大影响的平均应力。一般来说，在拉伸平均应力下进行的疲劳测试会比在压缩平均应力下进行的测试寿命短。这种影响也经常用R 值（载荷周期中最小和最大应力的比率）来表示。因此，疲劳寿命会随着平均应力（或 R 值）的降低而增加。

在疲劳模块中，应力-寿命模型没有考虑到这种影响。当使用这些模型时，需要选择在与操作条件相同的测试条件下获得的材料数据。

在累积损伤模型中，Palmgren-Miner 线性损伤求和法使用了 S-N 曲线。但是，在这个模型中，用 R 值依赖性来指定 S-N 曲线，并考虑了平均应力效应。

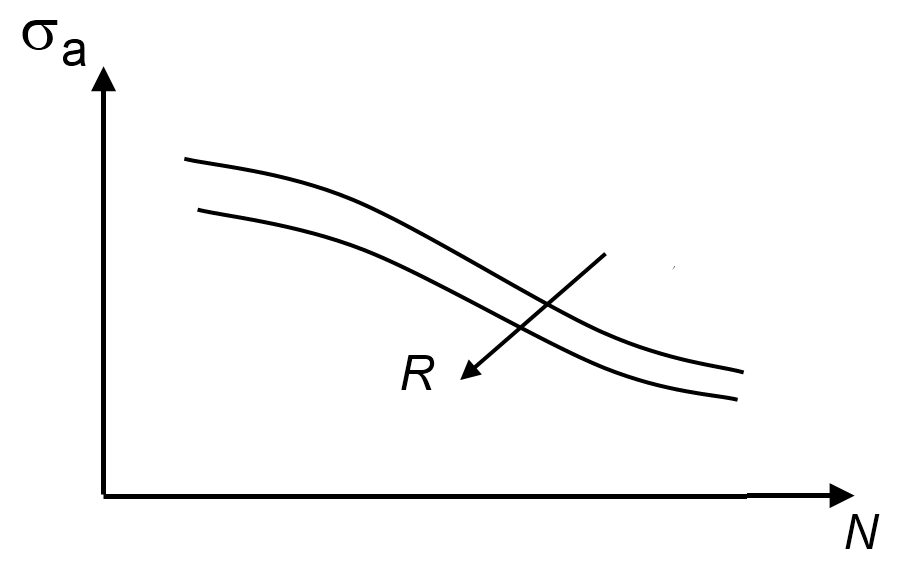
平均应力效应。

如果使用了材料库中的数据，并且疲劳数据是用最大应力指定的，那么可以使用以下公式轻松地将其转换为应力振幅：

其中，\sigma_a是应力振幅，\sigma_{max}是最大应力，R是 R 值。

获取 Findley 和 Matake 临界平面模型参数的建议

基于应力的模型似乎相当简单。例如，Findley 和 Matake 模型使用的表达式分别为

和

它们只取决于两个材料常数：f和k。然而，这些材料参数是非标准的材料数据，与材料的耐力极限相关。

请注意，两个模型的实际值f和k是不同的。获取解析关系有些麻烦，因为基于应力的模型是基于临界平面的方法，需要找到一个平面，使上述关系的等式左边最大。这基本上是通过使用莫尔应力圆将剪切应力和法向应力表示为方向的函数，将导数设为零来实现最大化，并简化所得关系。

这里我们不显示数据处理的不同步骤。对于 Findley 模型，材料参数与标准疲劳数据是通过以下等式关系描述的：

式中，R是 R 值，\sigma_U(R)是耐力极限。耐力极限的参数表明，应力与 R 值有关。对于 Matake 模型，这个关系比较简单，由以下公式给出

这两种关系都有两个未知的材料参数，因此需要从两种不同类型的疲劳试验中获得耐力极限。为了说明这一点，考虑这样一种情况：耐力极限R=-1是通过在拉伸值和压缩值之间交替的载荷获得的。第二种情况，载荷在零载荷和最大载荷之间循环，R=0。对于 Findley 模型，将得到

这个方程组必须通过数值求解。求解策略为：

• 消除两个方程之间的f，它可以被忽略，因为它总是作为一个线性项出现。
• 现在，我们有一个只关于k的非线性方程。由于k的变化相当小（通常在 0.2 和 0.3 之间），因此很容易求解，甚至可通过纯试错法。
• 使用计算出的k，用任一原始方程评估f。

对于 Matake 模型，两个疲劳测试导致

我们可以用解析法解决这个问题。

疲劳模型的实例

最后，给大家分享几个使用文中所讨论的疲劳模型的例子，欢迎查阅：

• 在圆柱形试样的高周疲劳分析案例中，Findley 和 Matake 模型被用来预测疲劳。
• S-N 曲线被用于支架教程模型中。
• 具有 R 值依赖性的 S-N 曲线被用于带切口的框架模型的疲劳预测。