CFD 仿真中如何设置入口和出口边界条件

在建立流体流动仿真模型时，我们通常会关注大型系统中的单个（或少数几个）组件，例如水处理厂中的泵或沉淀池。这自然地引出一个问题：在正确表征流动的情况下，应用边界条件的合适距离是什么？这篇博客，我们将探讨入口和出口边界的距离对可压缩性忽略不计的均质流体的内部和外部流动的影响。

内部流动的入口和出口边界设置

CFD 仿真常常对计算资源要求较高，因此我们会在模拟中尽可能地减小自由度。但如果过度操作，可能会得到入口和出口边界相交的几何体。以一个横截面为半圆形的 90°弯管仿真为例来说明。

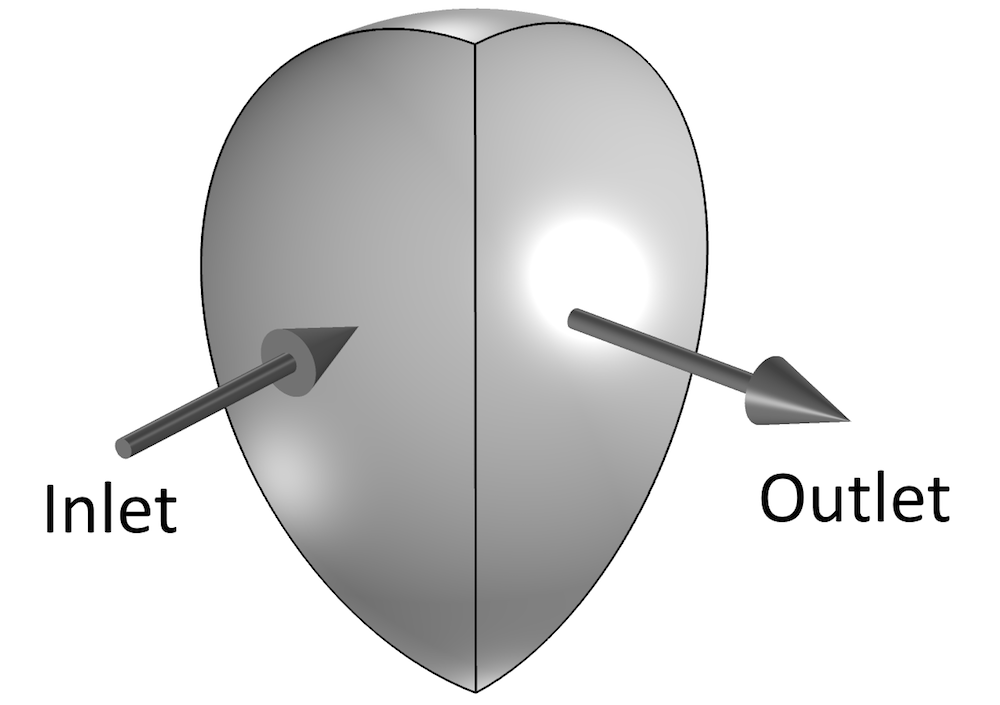
具有半圆形横截面和 90°弯管的管道。

如果基于上图显示的几何结构设置模拟，入口和出口边界共用一条边。大多数情况下，仅这个问题本身就可能导致严重的收敛问题。不过，在这个特殊示例中，解在迭代几次后就实现了收敛。此外，我们还考虑一种合理的模拟设置，即将管道的入口和出口延伸至管道半径的10 倍长度（如下图所示）。

带延伸的入口和出口管道的 90°弯管。

基于水力直径D_{h}=4A/P（A是横截面面积，P是横截面周长），雷诺数为 120 的条件设置模拟。将入口处设置为均匀速度分布，出口处法向应力设置为 0。下图显示了两种设置下弯管处的压力分布情况，左侧为入口和出口延伸的弯管模拟结果，右侧为入口和出口不延伸的模拟结果。对于入口和出口延伸的管道，用弯管处的压力减去下游边界上的平均压力，使两种模拟结果在此边界上的平均压力都为 0。

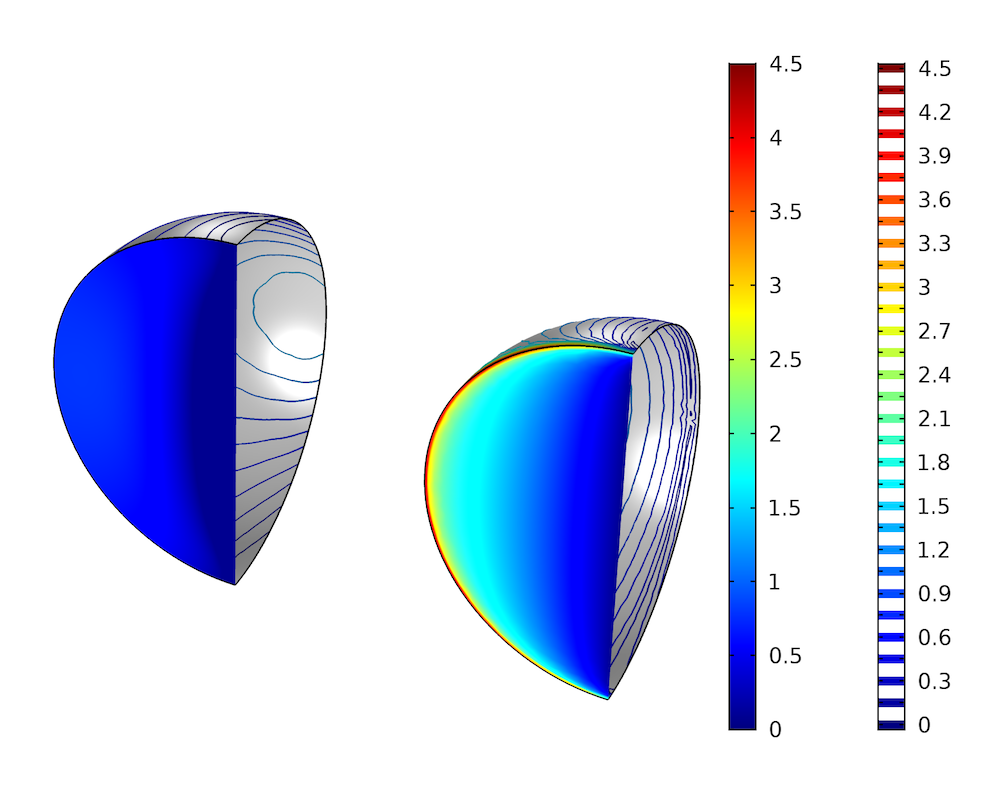
通过横截面为半圆形的90°弯管管道上的压力变化，包括上游边界的压力表面图和管壁的等压线图。左侧绘图显示了入口和出口延伸的弯管模拟结果，右侧绘图显示入口和出口无延伸的弯管模拟结果。

入口和出口无延伸的弯管仿真结果显示了较显著的压力变化。由于应用的均匀速度分布和壁面处的无滑移边界条件两者不相容，靠近入口的壁面上存在急剧变化的压力梯度。左侧显示了弯管上游侧的压力分布更加均匀，这表明当流动到达弯管时已经充分发展。然而，压力分布并非完全均匀，在靠近急转弯处，压力略低，这表明弯管对上游流动产生影响。我们还观察到，上游边界对面的管壁上有一个驻点。弯管处的压力损耗系数由下式定义

(1)

对于入口和出口无延伸的管道，该值为 2.3，对于入口和出口延伸的管道，该值为 0.60。通过观察速度场可以了解更多信息。

横截面为半圆形的90° 弯管中的速度和流线分布。

上图显示了弯管上游四个位置和弯头下游四个位置的速度分布剖面，以及中心平面的流线。在弯管上游，可以观察到均匀的速度分布如何演变为充分发展的速度分布。在弯管处，可以明显观察到管壁面向入口管道的驻点及相关回流区。在急转弯的下游还有一个回流区，可以看到，在出口管道的末端首先形成充分发展的速度分布。所有这些现象在简单的几何结构（只包含 90° 弯管）中是不存在的，因此使用该结构计算得到错误的压降也就不足为奇了。

入口和出口边界特征中包含的充分发展的流动选项，可以避免设置过长的入口和出口管道。上述两幅图中的结果显著表明，要获得良好的结果，应该在远离弯管一定距离处应用这些条件。那么，需要在上游和下游多远的位置应用充分发展的流动选项呢？如果将管道入口和出口分别从弯管处延伸 1 倍半径长度，弯管的压力损耗系数将变为 0.54，如果沿每个方向延伸 2 倍半径长度，压力损耗系数变为 0.58。自此开始，压力损耗系数向 0.60 收敛的速度会变慢。因此，在这个示例中，沿每个方向延伸 2 倍半径长度可能是最优方案。

随着雷诺数的增大，弯管下游的回流区长度将增加，最终变得不稳定。对于雷诺数为 1200 的情况，如果管道末端应用了充分发展的流动选项，当管道出口延伸超过 20 倍半径长度时，损耗系数不再有明显变化。基于管道入口长度的相关性，当流动为层流时，

(2)

当流动为湍流时，

(3)

由上述公式可以估算出距离弯管下游多远处可以获得充分发展的流动分布。请注意，湍流入口长度通常比雷诺数高的层流入口长度短。入口长度要达到水力直径O(10^2)，雷诺数必须达到O(10^8)。

对于雷诺数分别为 120 和 1200 的两种层流情况，由公式(2)计算得到的入口长度分别约为半径的 7.5 倍和 75 倍。通过在出口处应用充分发展的流动选项，当出口管道近似为入口长度的 1/3 时，得到了理想的结果。

对上游的影响将随着雷诺数的增大而减小，这是因为纳维-斯托克斯方程的椭圆特性会随着雷诺数的增大而减弱。我们可以通过观察类似几何结构的势流来预估对上游产生影响的区域。

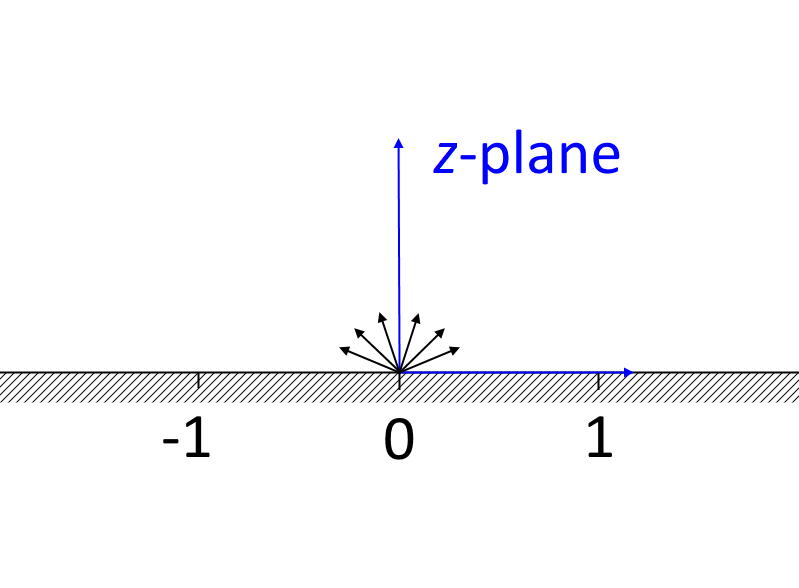
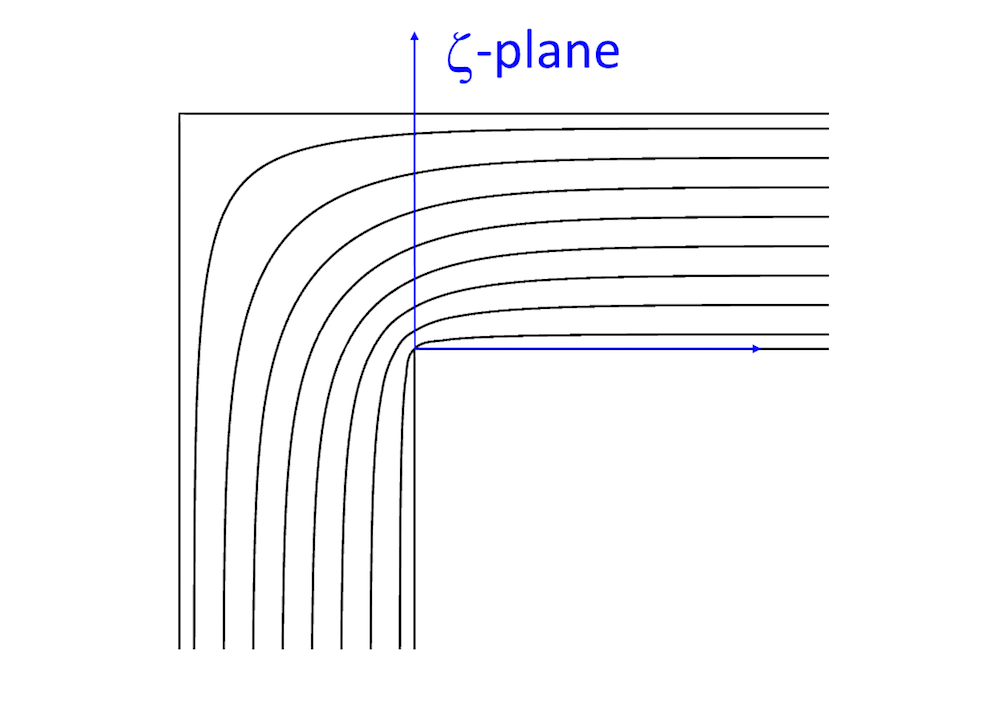
使用 Schwarz-Christoffel 变换将上半个平面映射到 90° 急弯管。

使用 Schwarz-Christoffel 变换（参考文献 1），将复z平面的上半个平面映射到复\zeta平面的 90° 急弯管。入口位于\zeta平面的-i\infty处，对应于z平面原点的源，而两个平面的出口都位于\infty处。\zeta平面中弯管的外角和内角分别对应于z平面中的点 -1 和 1。\zeta平面内的速度场通过下列隐式形式计算

(4)

下图显示了在势流解中，沿内壁的压力损耗系数与弯管上游无量纲距离之间的函数关系。

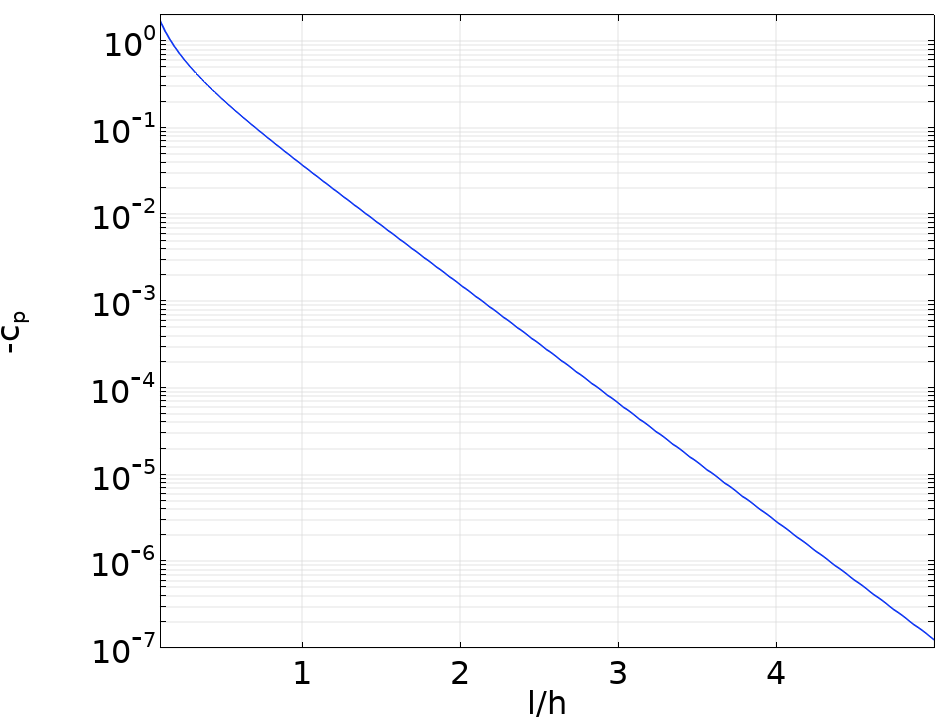
90° 急弯管上游内壁的压力系数。

图中，压力系数是通过局部压力与距离较远的上游压力之差获得的，h是管通（或通道）宽度。我们发现当上游到弯管的距离为两个管道宽度时，压力系数为O(10^{-3})。因此，如果在入口处应用充分发展的流动选项，只需将入口管道向上游延伸几个水力直径长度即可。

重力分析

当模型中考虑重力时，入口和出口边界特征中的充分发展的流动选项会附带静水压力补偿选项（不可压缩流动）或静水压力补偿近似选项（弱可压缩或可压缩流动）。对于不可压缩流动，附加选项可以精确计算出边界上的静水压力分布，而对于弱可压缩流动和可压缩流动，则能得到可靠的近似值。当入口或出口边界处的流动明显分层时（例如多相流），必须格外小心。对于这些情况，建议添加一个流动方向与重力矢量平行的腔室。

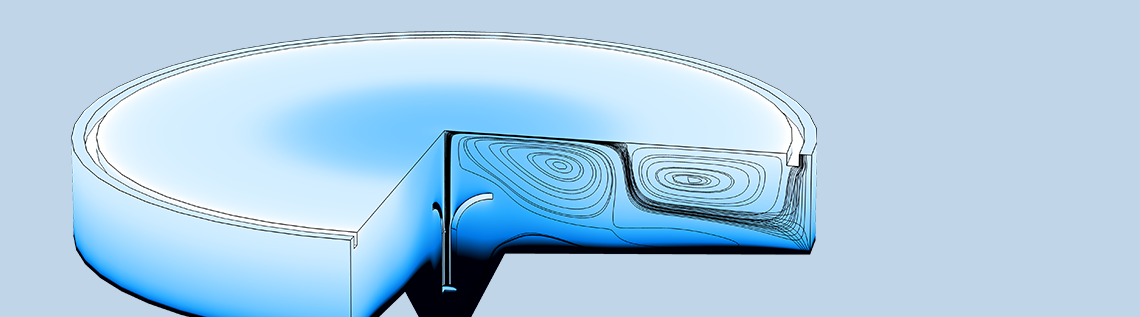
不考虑重力时也可能出现问题，如下图所示的一个停留时间较长的大型沉淀池。在沉淀池中，允许悬浮（重）相沉淀并通过底部出口流出，轻相则通过靠近外缘的环形出口垂直排出。图中，灰色流线代表轻相的速度场，黑色流线代表重相的速度场。一小部分重相通过轻相出口排出。由于重相的流动方向与重力相反，当一些悬浮颗粒再次下降时，在外缘附近形成一个小涡流。这个小涡流会对时步产生负面影响，导致总求解时间较长。补救办法是添加一个溢流孔（溢流堰），使流动方向与重力相同。

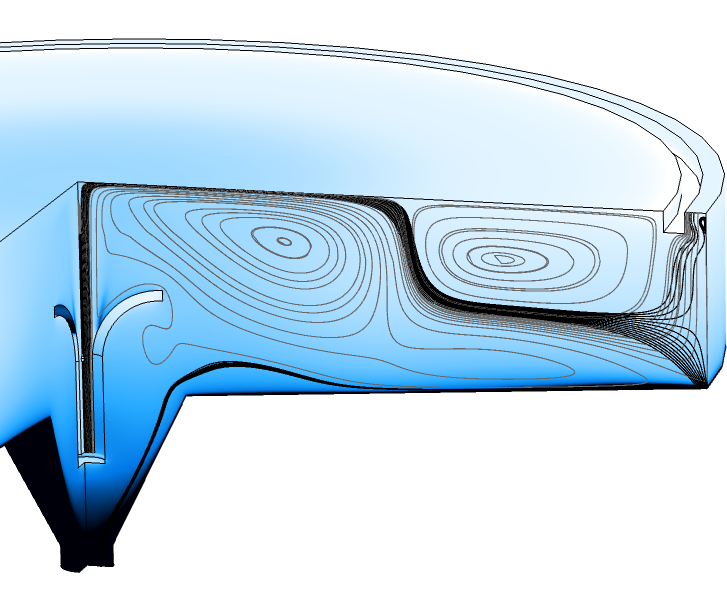
沉淀池中分散相的体积分数（彩色图）和流线，灰色表示轻相，黑色表示重相。

模拟热羽流时也会出现流入和流出边界相交的情况，如下图所示。在这个示例中，没有在流入边界（图中的圆柱面）指定入口边界条件，而是应用了开放边界特征。在开放边界特征和出口特征（顶部边界）中，都应用了静水压力补偿近似选项。添加这个选项很有必要，因为模型中浮力产生的压力比静水压力小三个数量级。同样，出口特征中的抑制回流选项也必不可少。

湍流热羽流，显示了速度大小（用彩色绘制）和减去静水压力的等值线。

顶部边界处等值线的微小扰动是因为和恒定压力不一致造成的，使用非等温流动多物理场耦合节点中的布辛涅斯克近似选项可以消除这些干扰。

外部流动的入口和出口边界设置

在一些外部流动应用中，例如车辆和建筑物周围的流动，正确设置边界条件也至关重要。通常将入口边界上的恒定速度矢量和出口边界上的恒定压力设置为远离障碍物的边界条件。那么问题又来了，在距离障碍物多远的位置应用这些边界条件，才不会对解造成影响？对于外部流动，事实证明该距离随模型的空间维度变化。对于二维模型，所需距离比三维和二维轴对称模型大一个数量级。让我们再次以理想的势流解为例，尝试理解其中的原因。

对于障碍物周围的外部流动，固体表面的边界层会产生涡流。障碍物不同侧面的边界层可能在会尾部边缘汇合，形成一个薄层涡流，并被平流输送到下游形成尾流。如果任何一侧的边界层由于不稳定性或尖角的存在而与障碍物分离，尾流将更宽。无论哪种情况，流向下游的涡流都将被限制在尾流内，尾流外的流动近似于无旋流动。

NACA 翼型周围的湍流。剖面图上部的边界层在后缘前方分离。

障碍物及其尾流取代了自由流的流线，我们可以将远离障碍物的流动看作是均匀流动与源的总和。

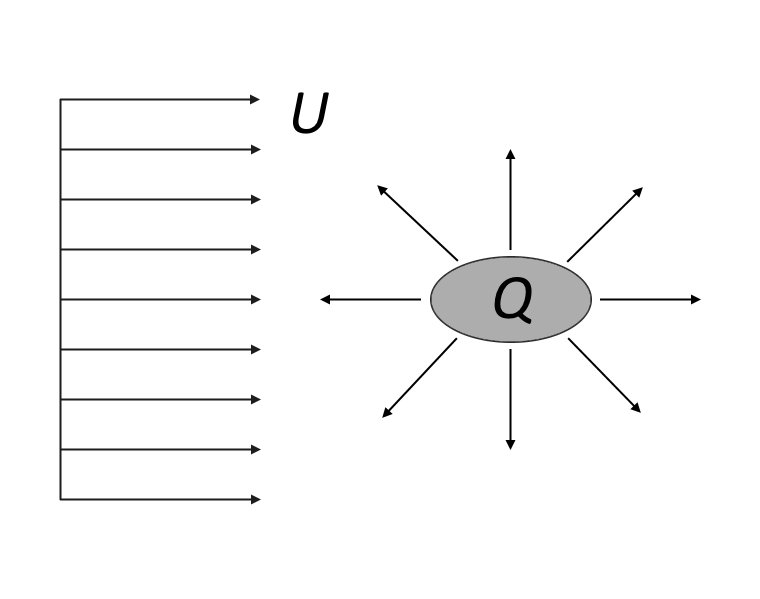
远离障碍物的势流及其尾流。

二维和三维模式下产生的速度场可以表示为

(5)

其中R=\sqrt{x^{2}+y^{2}},r=\sqrt{x^2+y^2+z^2}，源位于原点，自由流则流向正x方向。

无论二维还是三维，源强度都与障碍物的大小有关。对于源的x位置，在二维模拟中，流线的位移为y_{0}=Q/(4U)，在三维模拟中，流线的位移为r_{0}=\sqrt{Q/(2\pi U)}。

下游的极限值为别是y_{\infty}=Q/(2U)和r_\infty=\sqrt{Q/(\pi U)}。在目前的估算中，无论是二维模拟中的2y_{0}和2y_\infty，还是三维模拟中的2r_{0}和2r_\infty，都可以表示障碍物的大小。其中，我们在二维模拟中使用d=Q/(2U)，在三维模拟中使用d=\sqrt{2Q/(\pi U)}。根据伯努利方程，可以获得远距离处压力系数的估计值

(6)

将势流速度场与源强度的估计值一起代入，我们可以得出

(7)

因此，压力系数在二维模式下减小为d/R，在三维模式下减小为(d/r)^{2}。为了降低如O(10^{-2})外部边界条件的影响，在二维模拟中，必须将计算域的外部边界定位在 100 倍障碍物大小的距离之外，在三维模拟中，定位在 10 倍障碍物大小的距离之外。

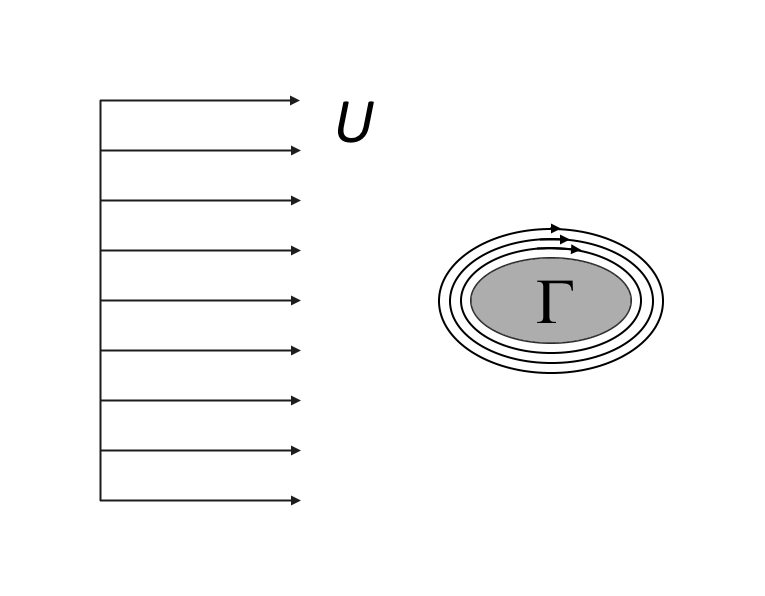
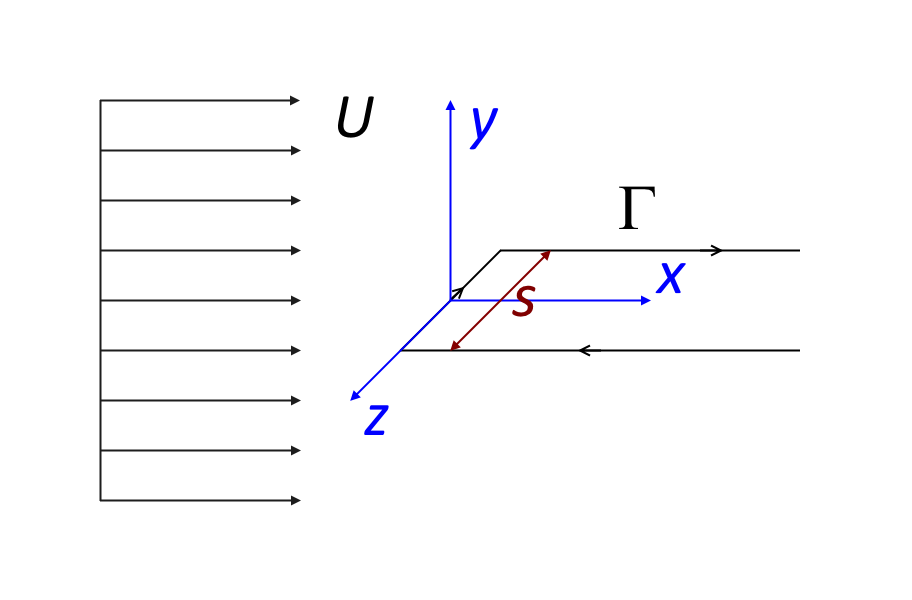
根据障碍物的形状和方向，涡旋脱落可能导致产生侧向力（升力）的环流。离障碍物较远的势流可以用均匀流和点涡（二维模拟）或均匀流和马蹄形线涡（三维模拟）来近似。

带环量（升力）的障碍物周围的势流。在二维模拟中（左），势流包含 x 方向的均匀流和位于原点的点涡。在三维模拟中（右），势流包含 x 方向的均匀流和马蹄形涡流，马蹄形涡流在 z 方向的跨度为 s，在 x 方向延伸到无限远处。

在距离障碍物很远的位置，对应于上图的势流速度场由下式给出

(8)

请注意，通过将z设置为零并让s\rightarrow\infty，可以根据三维解获得二维解。在大部分可实现的案例中，环量可以通过下式与障碍物的自由流速度和流向尺寸（弦）c相关联

(9)

其中，\alpha是攻角，-\beta是“零升力”角（都以弧度为单位）。

后者由障碍物的形状（曲率）决定，比如，机翼的弧度。将渐进势流解和\Gamma的表达式代入压力系数的定义中，得到

(10)

总偏转角\alpha+\beta必须至少比 1 个单位小一个数量级，这样\Gamma的估算值才成立。对于球体，维度d、c和s相等。因此，环流对外部边界附近的限制不如源的限制严格。

对于机翼来说，三个维度的数量级各不相同s\sim 10c\sim 100d。在二维模拟中，由于d\sim c(\alpha+\beta)，点涡造成的限制与源产生的限制大小相等。如果要对三维机翼进行单独建模，那么线涡造成的限制将比源造成的限制严重 100 倍。通常，机翼通过d\sim c附在机身上，在这种情况下，三维模拟中两种限制的数量级相同。下图显示 14° 迎角下NACA 0012 机翼周围流动的二维仿真。为了将外部边界条件的影响最小化，我们在每个方向上将域延伸 100 个弦长。在该示例中，相关长度比例为c\alpha，对于对称剖面，\beta=0。根据以上估算，压力系数为千分之几。

14° 攻角下 NACA 0012 机翼的二维仿真。

下图显示失速飞机以 20° 攻角飞行时失速状态的的三维仿真。计算域由半径为 15 米的半球和高度为 30 米的圆柱体界定。翼展长约为 18 米，机身直径为 2.4 米，最大弦长乘以攻角约为 1.3 米。插入这些数值得出的压力系数为百分之几，该值偏高。因此，如果将域延伸到离飞机更远的地方，仿真结果可能会有所改善。

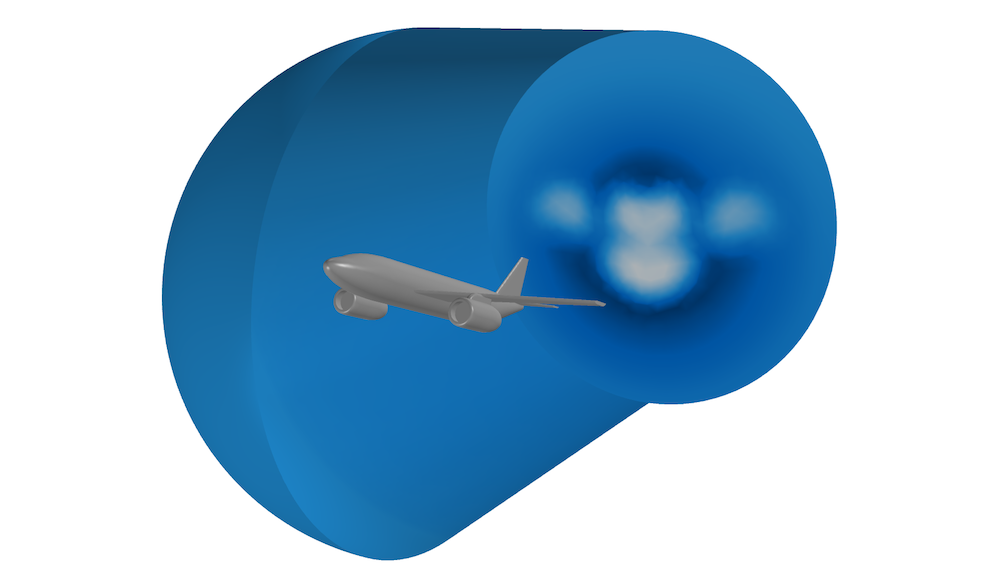
根据速度大小着色的计算域，用于失速状态的飞机。

关于设置入口和出口边界条件的总结

本文介绍了如何使用理想的流动理论和经验公式来确定入口和出口边界的合适位置。对于内部流动，使用层流和湍流的经验公式来确定获得充分发展的流动所需的管道长度，相应地向上游和下游延伸域能够显著提升流动仿真的精度。不过，这个长度会随着雷诺数增大而增加，尤其对于雷诺数高的层流而言，长度会变得过长。在入口和出口边界特征中使用充分发展的流动选项可大大缩短这一长度。在下游侧，将长度减少为原来的三倍是平衡精度和计算成本的合理值。势流模拟表明，设置上游入口的距离不需要超过几倍水力直径长度。当模拟中考虑重力作用时，可以使用 充分发展的流动 选项包括重力，但是当流动明显分层时（例如在多相流中），仍可能出现问题，对于这种情况，建议将出口重新定向为重力方向。

对于外部流动，使用势流理论估计在多远的距离范围内可以忽略障碍物周围流动引起的压力变化。我们发现，在二维模拟中，压力随\sim D/R变化，在三维和二维轴对称模拟中，压力随\sim A/R^2变化，其中，R是到障碍物中心的距离，D和A分别是映射到与自由流正交的平面上的障碍物的长度和面积。

希望这些估计结果对您建立自己的仿真模型有所帮助，不过，请记得验证结果。对于内部流动，当使用充分发展的流动选项时，最简单的方法是改变入口和出口通道或管道的长度，来查看结果是否发生变化。对于外部流动，使用这一选项可以检查压力边界上的速度与自由流动速度场的偏差不超过允许的容差（尾流除外），对速度边界上的压力也可以这样检查。

编者注：这篇博客更新于 2023/4/25。用于流体仿真的充分发展的流动边界条件已经是 COMSOL Multiphysics^®核心模块的一个可选功能了。