如何模拟全息页面数据存储系统

我们已经学会了如何在 COMSOL Multiphysics 中模拟一个简单的逐位全息数据存储模型，方法是选择合适的光束大小并实行记录和检索过程。今天，我们进一步学习如何模拟一个更困难、更复杂，但更真实和有趣的全息页面数据存储系统模型。

全息页面数据存储系统的仿真设计

在上一篇讨论逐位全息图模拟的博文中，我们介绍了全息数据存储，它在消费电子产品中的应用以及如何模拟逐位全息图。现在，我们将讨论另一种全息数据存储形式：页面数据存储。页面 是由空间光调制器（SLM）表示数据块是通过使用微机电系统（MEMS）或在硅（LCOS）液晶或者透射或反射。

正如之前的博文中提到的，全息数据存储的模拟传统上是通过光束传播方法进行的，这种方法可以处理非常大的计算域，但不能正确处理大聚焦角。另一方面，COMSOL Multiphysics 使用全波方法，可以处理任何类型的光束，但使用的内存相对较多。借助 COMSOL Multiphysics，我们可以在一个小的域中模拟一个页面(多字节)数据存储系统。为了演示，我们考虑一个类似于前面研究中使用的矩形域。这一次，我们将对一个字节(或八位)的数据进行加密。

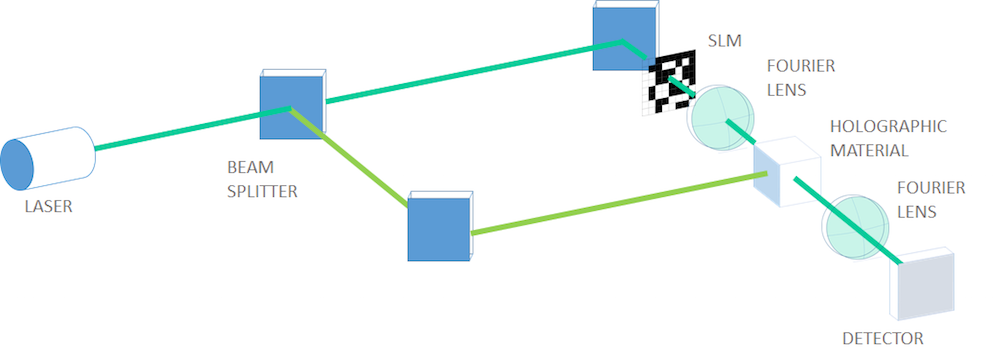
页面式全息数据存储的典型光学布局（我名字的字符代码在 SLM 中以二进制数据编码）。

对于这个模拟，我们将使用从我自己名字的一部分的母语字符代码转换而来的二进制数据。01001101，意思是“水”，可以在上图中 SLM 的第五行中看到。为了更真实，我们将使用一组傅立叶透镜将物体光束聚焦到全息材料中，以便在检索过程中将检索到的物体光束记录、扩展和可视化到检测器上。当然，我们不会对透镜进行建模，而是通过对 SLM 之后的电场幅度进行傅立叶变换，并将其作为入射边界上的散射边界条件中的入射场，来制作聚焦光束。

为了在检测器上对检索到的物体光束进行成像，我们再次对检索到的电场幅度进行傅立叶变换，并对范数求平方以获得电荷耦合器件(CCD)或互补金属氧化物半导体 (CMOS) 传感器检测到的强度作为信号。之后会进行更多的信号处理，以产生更清晰的信号，并将误码率降低到一个明显更小的水平，但我们在这里不讨论这个过程。

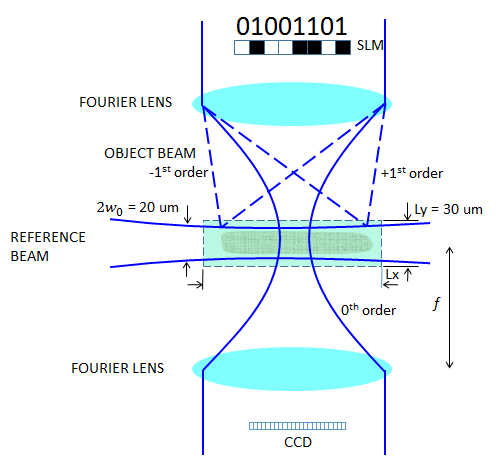
一种全息页面数据存储系统，携带一个字节的数据。

定义参考光束

在我们之前的讨论中，我们使用了稍微发散的超高斯光束。对于这个模拟，沿着参考光束传播的方向，磁畴尺寸将不可避免地变宽，这将在后面讨论。因此，如果我们使用发散光束，光束最终会接触到边界，这需要避免。我们将添加以下二次相位函数，以使光束稍微聚焦在域的中间，而不是发射左侧边界上具有平坦相位的 10 um 光束，假设平面外电场求解为

其中，w_r是参考光束的束腰半径，n是全息材料的折射率，k_0是真空中的波数，R_r是在远处的波前曲率x，从光束腰(焦平面)位置开始

其中，x_R=n \pi w_r^2/\lambda_0是光束几乎是直的瑞利范围。

对于，w_r= 10 um，\lambda_0= 1 um，以及n= 1.35，x_R= 424 um。我们稍后会看到，这个数字远远大于我们的域大小，这意味着光束在计算域中几乎是准直的。为了定义波前曲率，我们借用了近轴高斯光束公式。我们忽略了恒定相移和 Gouy 相移，它们在这里是不必要的。下图显示了如何进入左边界处具有右曲率的入射场(x=-L_x/2).

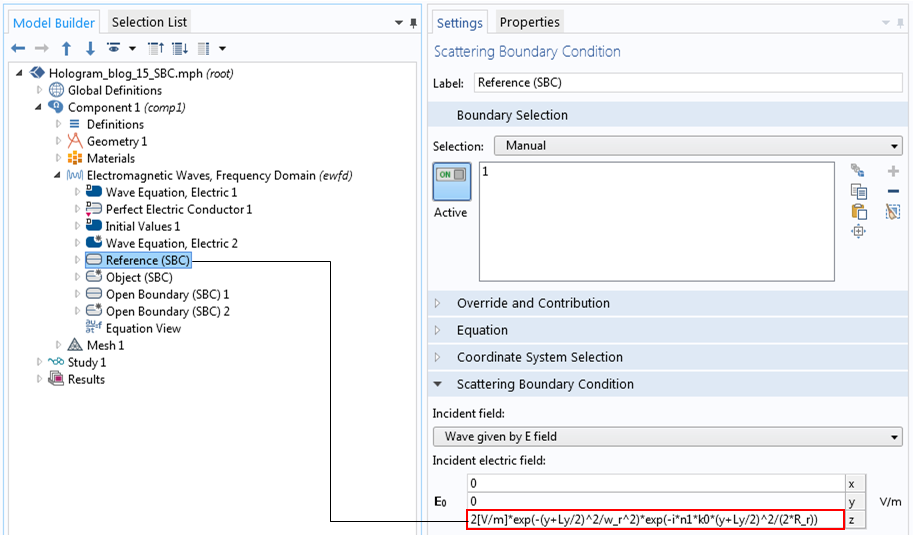
定义具有波前曲率的参考光束。

定义物体光束

当我们使用 10 um 的束腰半径时，垂直域的大小L_y，30 um 就足够大了。这里最大的障碍是如何确定水平域的大小L_x，对于物体光束入口。现在，物体光束通过的孔径是 1 x 8 SLM，具有 8 个像素。SLM 就像一个衍射光栅，周期为2d。当物体光束通过 SLM 并被聚焦时，零级光束聚焦成所谓的艾里环半径的圆，高阶衍射光束将以对应于衍射级的角度扩散。

为了从 SLM 获得足够的信息并将正确的数据存储在全息材料中，我们希望至少捕获一阶光束（0^th和 ±1^st）。否则，我们可能会得到一些检索到的信号，但该信号可能无法完全恢复原始数据。我们只接受第一阶的另一个原因是，所有其他更高阶的强度都太弱而无法记录在全息材料中。

第一个要求是零阶束腰半径w_0，必须是 10 um，这决定了透镜系统的数值孔径 (NA)。艾里环半径w_0, 由艾里环半径公式给出

其中，\lambda_0是空气中的波长。

我们希望艾里环半径为 10 um。根据这个要求，对于给定的w_0和\lambda_0，我们得到 NA

另一方面，NA 最初被定义为

其中，\theta是聚焦角，N是 SLM 的数量，d是 SML 像素的一半大小，f是傅立叶透镜的焦距。

由这个等式，f/d可推导为

我们应用一阶光栅方程

其中，\alpha_1是一阶光束的衍射角。

我们得到偏差w_1一阶光束的光束位置与零阶光束相距一定距离f，

插入已知数，N= 8 和w_0= 10 um，得到w_1= 65.6 um。添加一些余量来捕获“整个”一阶光束，一半L_x可能是 80 um；也就是说，L_x= 160 um。值得一提的是，这个特殊的数字是全息技术的关键要素之一。

除了这个数字，\lambda_0,f, 和d未确定。现在我们知道了所有的域大小，我们可以从最大网格大小估计所需的网格数，\lambda_0/6/(2n\sin(\beta/2)) = \lambda_0/(6\sqrt{2}n)，其中，n是全息材料的折射率，并且\beta是物体光束和参考光束之间的交角。对于我自己电脑的 RAM 容量，\lambda_0= 1 um 似乎是最短的波长。然后，我们得到f/d= 131.1，其中的数字f和d是相互依赖的。让d= 40 um，f= 5.2 mm，我们现在拥有了所有的模拟参数。

为了准备 1×8 像素数据，我们可以定义图元内置矩形函数来表示单个像素。为了产生像素数据，矩形函数被移位并相加。01001101定义为一个解析函数，如下图所示。开放的子孔径代表“1”。

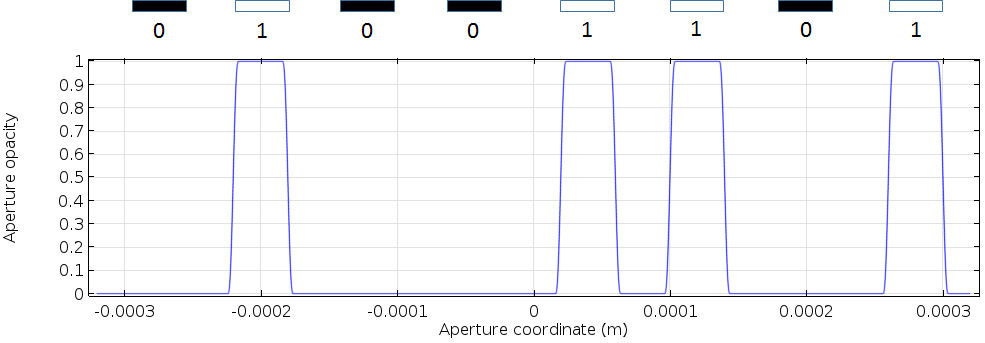
SLM 孔径不透明度函数，表示的八位数据01001101。

在 COMSOL Multiphysics中实现傅里叶变换

接下来，我们聚焦物体光束。在傅里叶光学中，由傅里叶透镜聚焦在焦平面上的输入电场的图像是输入场的傅里叶变换。由具有焦距f的傅里叶透镜聚焦的像平面中的复电场振幅计算公式为

其中，u是傅立叶/图像空间中的空间坐标，u/(f\lambda_0)表示空间频率。

我们需要使用额外的软件来实现傅立叶变换吗？不需要。通过使用 COMSOL Multiphysics，所有需要的功能都包含在一个软件包中。您也可以在与其他有限元计算相同的平台的图形用户界面中使用 COMSOL Multiphysics，作为一个方便的科学计算软件。

下图显示了“设置”窗口，后面是页面数据的傅立叶变换的结果01001101，由 COMSOL 软件计算。

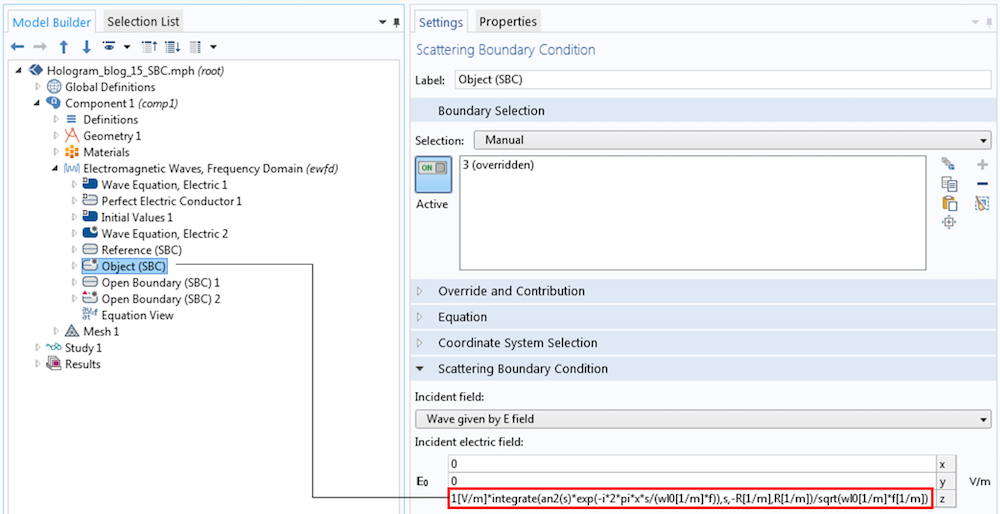
入射物体光束的设置，即 SLM 后电场幅度的傅里叶变换。

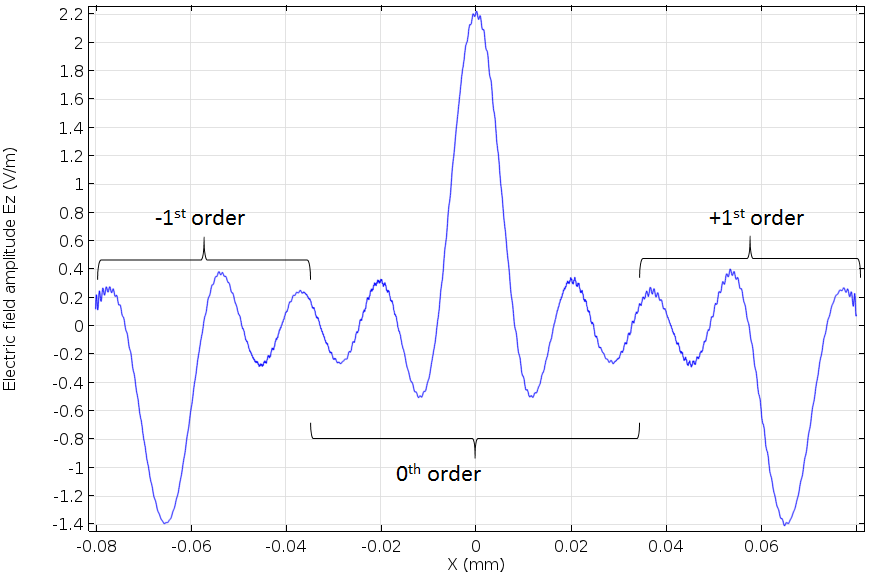
将计算得到的入射物体光束作为二进制数据01001101的傅里叶变换。

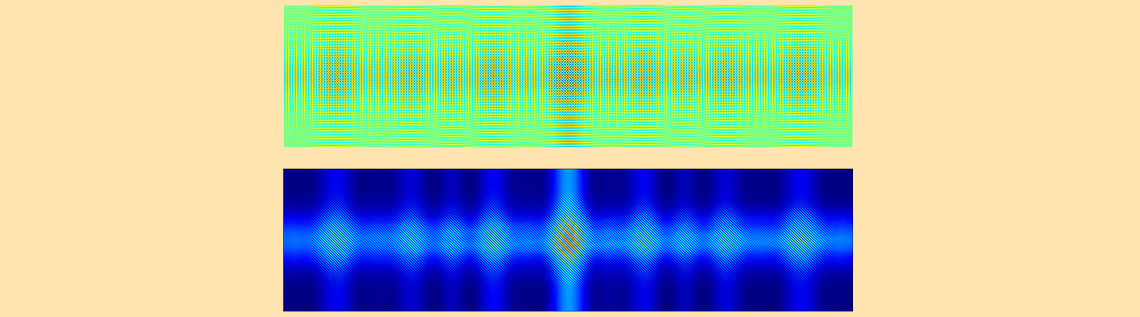
中心光束是零级光束，相位相反的两个侧光束是一级光束。这是典型的夫琅禾费衍射图。正如我们之前计算的那样，我们的计算域正好适合这三个光束。该电场幅度作为目标光束的电场边界条件给出。下图是页面数据记录的结果。

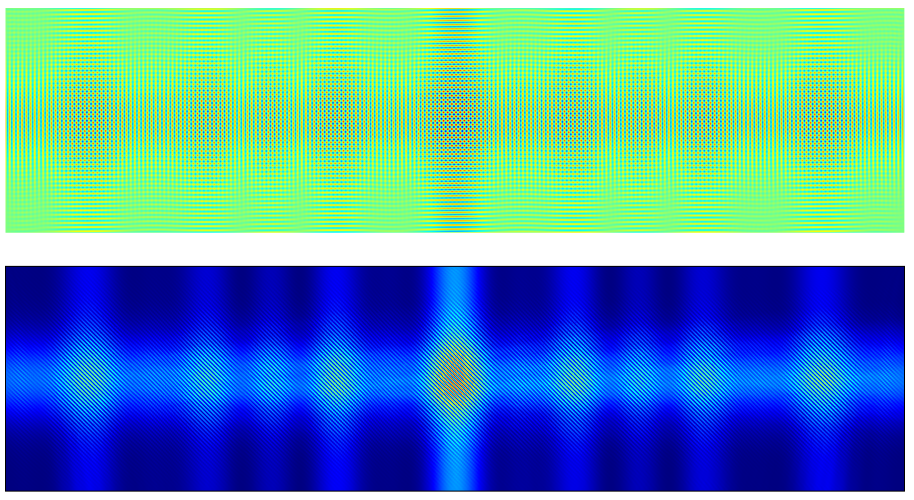
页面数据记录的电场幅度(顶部)和强度(底部)。

由于我们的编码和加密工作，我们的全息模拟开始变得更加有趣。我名字的数据已经被工业标准编码，然后转换成二进制代码。然后，它被傅立叶透镜进行傅立叶变换，这可以被认为是另一个加密过程。最后，代码被加密成全息图。当然，你不能只看上面的任何一张图片就破解代码。

检索全息数据

接下来，我们继续进行数据检索步骤。如上一篇博文所述，为了检索数据，我们可以使用相同的 COMSOL Multiphysics 特征来打开和关闭这些功能。我们通过添加具有用户定义的折射率的波动方程，电气2节点来实现这一点，它指定了调制指数。

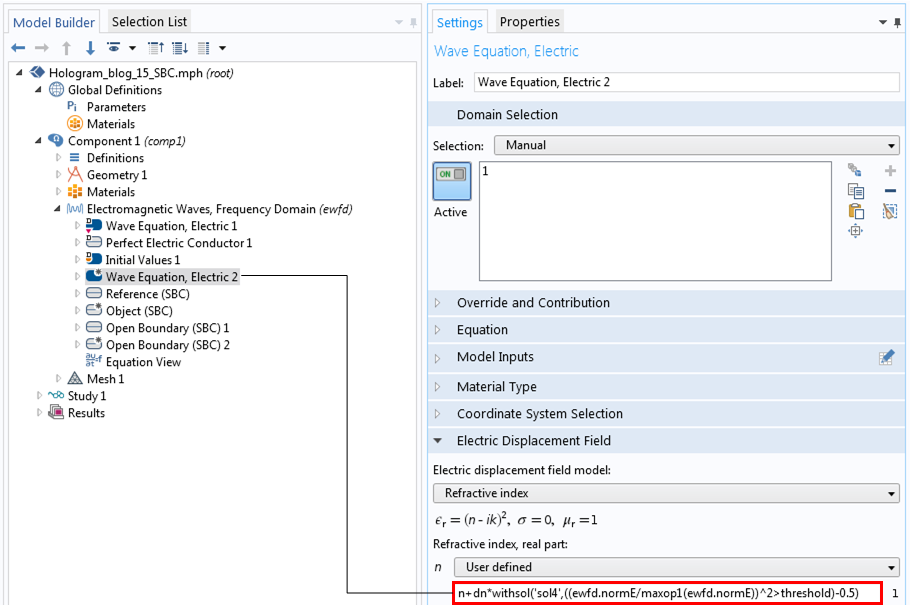
调制折射率的设置窗口。

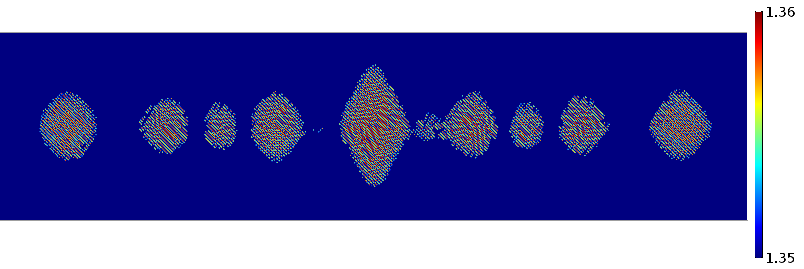
调制折射率。调制幅度对应于电场强度超过阈值的位置。

通过关闭目标光束并保持参考光束打开，以及具有调制指数，我们获得了检索模拟的结果。

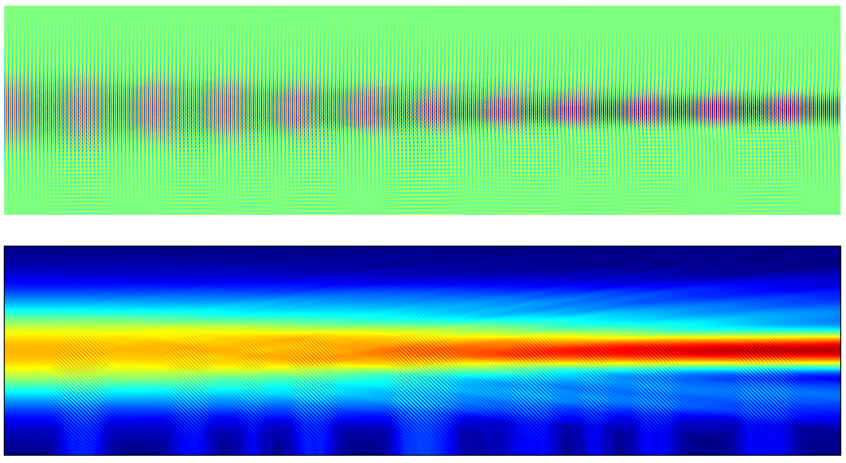
用于页面数据检索的电场幅度(顶部)和强度(底部)。

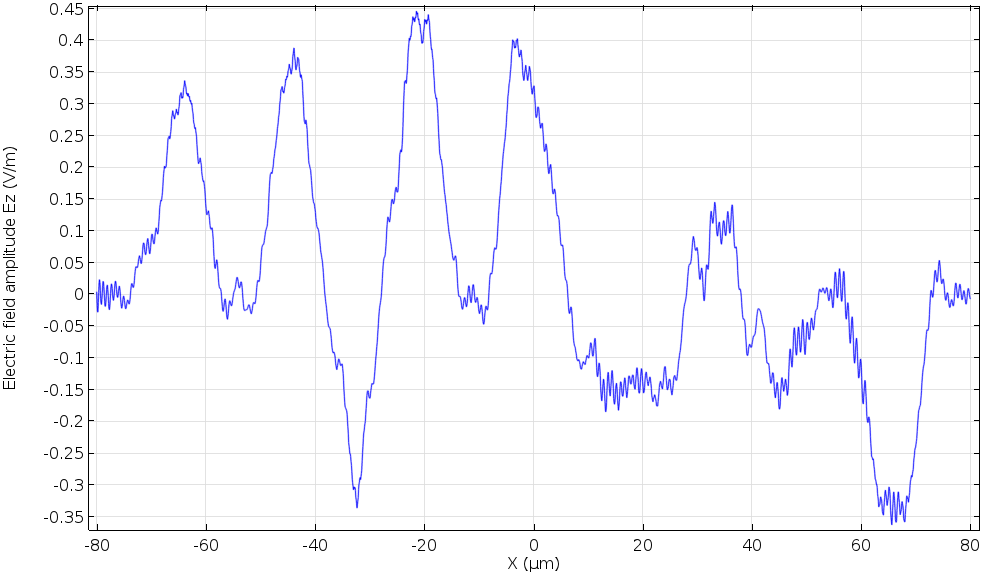
页面数据检索过程中底部边缘的电场幅度(横截面)。

现在，我们想通过使用另一个傅里叶透镜将这些检索到的数据成像到 CCD 表面上。为此，我们将再次对检索到的电场幅度进行傅立叶变换，并取这个量的平方。下图是最终结果。CCD 检测到1原始代码中的位置，01001101。我们终于又看到代码了！

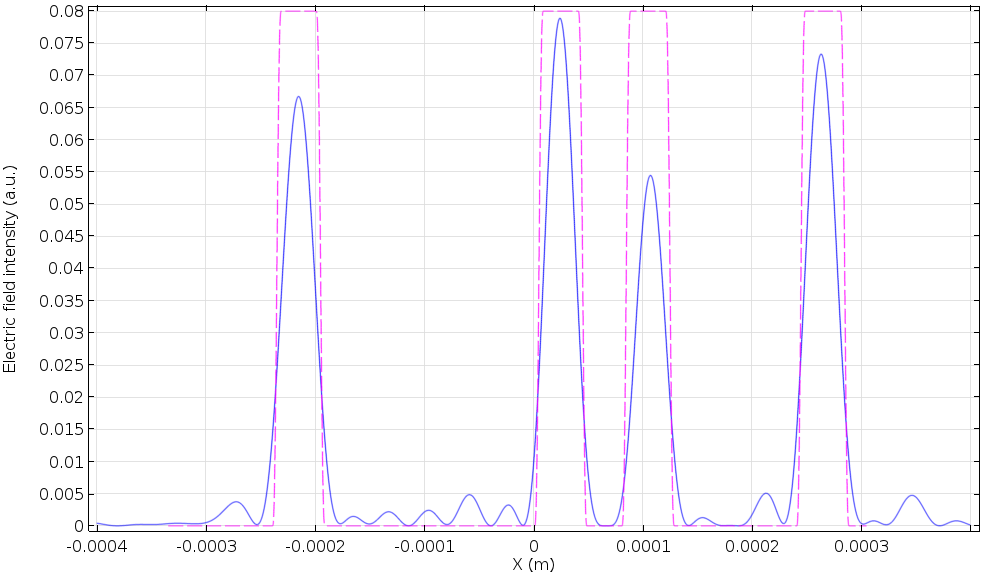
在 CCD 表面检索到的数据。虚线表示1在原始代码中的位置。

全息页面数据存储总结

我们使用 COMSOL Multiphysics 的波动光学功能实现了全息页面数据存储模型。尽管严格的 Maxwell 求解器说服我们更多地关注某些特定限制，但我们还是能够瞥见由我们在模拟之前执行的设计计算所产生的全息图。我们还介绍了 COMSOL Multiphysics 作为科学计算器的一些有用和方便的用法。正如我们所了解的，COMSOL 软件可以在一个环境中执行所有这些任务，同时执行顺序有限元计算和其他科学计算。

拓展阅读

• 查看 COMSOL 博客:
  • 查看本系列的第一部分，了解全息数据存储简介
  • 阅读有关傅立叶变换的内置积分运算符的信息
• 通过 JW Goodman 的 Introduction to Fourier Optics 一书，了解更多傅里叶光学知识