
载流子动力学在半导体器件的瞬态行为和频率响应中起着重要作用。本文我们使用 COMSOL Multiphysics®软件的附加产品——半导体模块中的两个 PIN 整流器教程模型来演示如何模拟动态效应。
半导体模块中的 PIN 整流器模型
自 COMSOL Multiphysics®5.4 版本起,COMSOL 案例库中提供了两个 PIN 整流器模型,用于模拟功率二极管的开启和关闭的瞬态过程。这些过程分别被称为正向恢复和反向恢复。
正向恢复是通过理想的输入电流曲线来模拟的,即电流从零开始线性增加到持续稳定的峰值电流。在指定电流输入的导通时段内,器件电压出现了短暂的尖峰,这是因为在漂移区域中积累额外的电荷载流子使二极管完全导通所需的时间有限。
反向恢复教程使用了一个更复杂的模型,该模型结合了 COMSOL®软件的集总电路功能,更真实地模拟了电感负载和续流二极管。该模型还包含了带隙变窄和载流子散射效应。对于反向恢复,由于在导通状态期间漂移区中存储了大量电荷载流子,二极管在施加电压转换后的短时间内仍保持正向偏置模式。
正向恢复模型
正向恢复模型教程是基于 Baliga 编写的书(参考文献 1,P242)中的器件模型建立的。该结构长 80 um,基底 n 掺杂为 5e13/cm3,外部边界处 n 掺杂和 p 掺杂的峰值为 1e19/cm3。电流驱动的 PIN 整流器具有恒定的缓变率 1e9、2e9 和 1e10 A/cm2/s,其稳态电流密度为 100 A/cm2。
使用带截断的斜坡函数指定输入电流曲线。为了帮助瞬态求解器准确求解,使用事件接口标记在电流斜坡 (t_on) 结束时施加的电流斜率的突然变化,如下面的屏幕截图所示。
![]()
使用事件接口来标记施加电流斜率发生突变的时间。使用半导体平衡研究步骤求解关闭状态作为以下瞬态研究步骤的初始条件。
设置瞬态正向恢复模型
为了与所考虑的物理系统保持一致,瞬态研究应该从对应于系统实际初始状态的初始条件开始。在正向恢复的情况下,初始状态是系统中流过电流为零的关闭状态。初始条件的电势和载流子浓度是预先未知的,因此需要通过求解稳态方程来计算。在关闭状态下,系统处于平衡状态,因此可以使用半导体平衡研究步骤。详请参阅上图中的研究1 > 步骤1。该研究步骤的结果将自动用作下一步瞬态研究的初始条件。
为了获得更好的精度,瞬态研究步骤的相对容差设置为 1e-5。
PIN 二极管的正向恢复结果
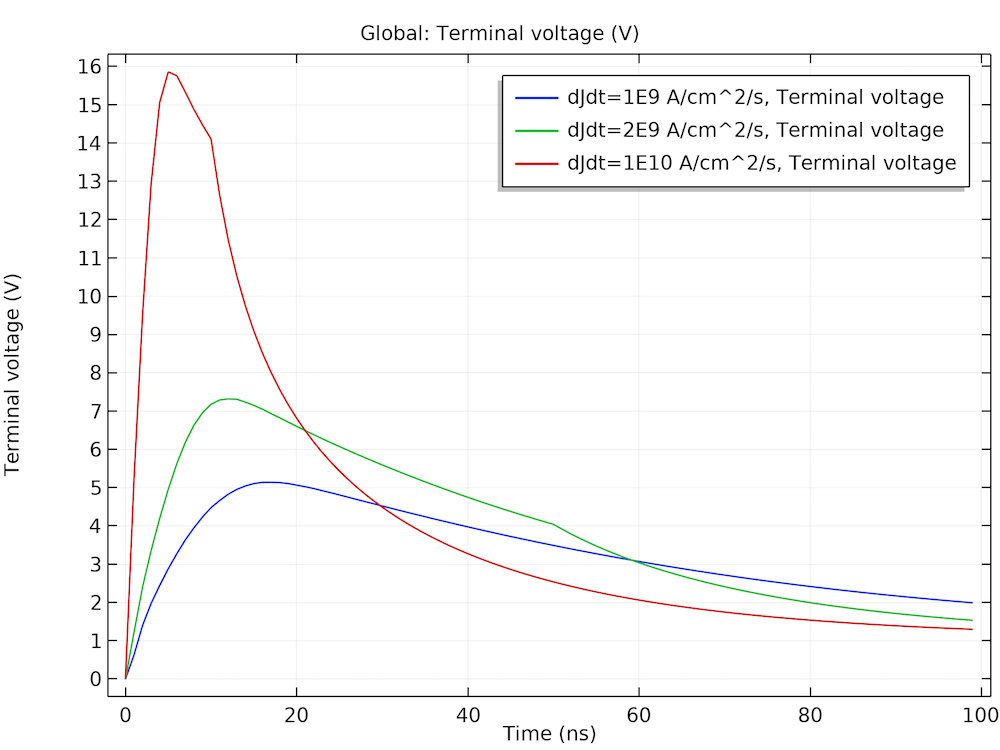
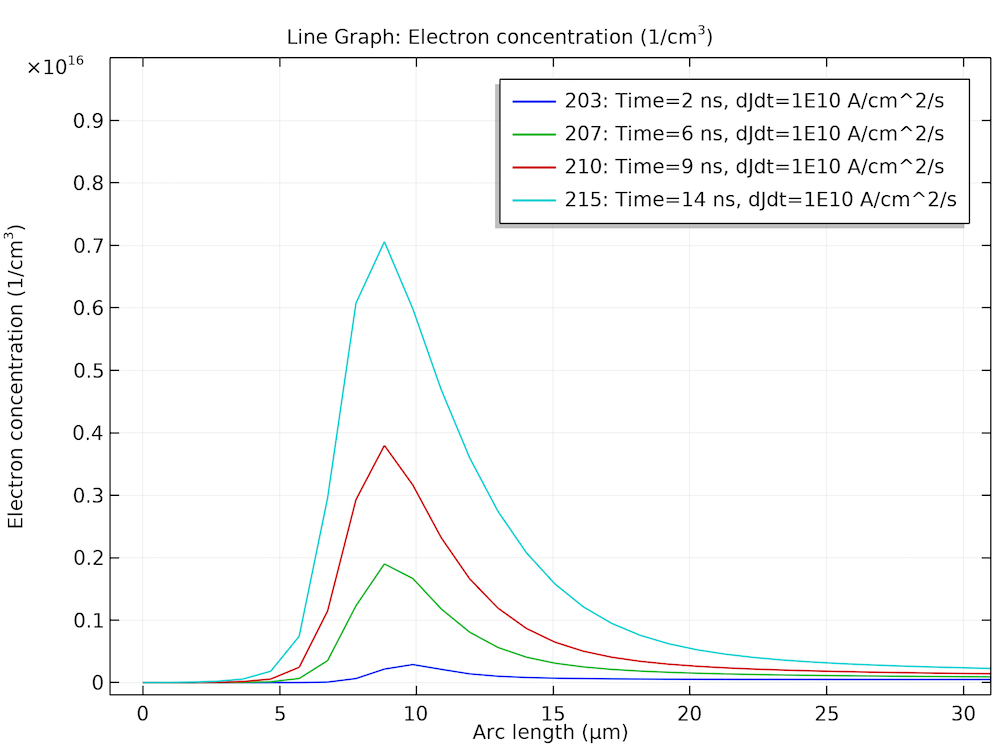
下图左显示了三种电流斜坡速率的器件电压的时间演变。右图显示了在电流斜坡速率为 1e10 A/cm2/s 时的几个选定时间点的电子浓度。它们表现出如预期的那样的典型的行为,即在开启过程中,额外的电荷载流子在漂移区初始积累。这些图与参考文献1中的图 5.30 和图 5.31 非常吻合。
左图:正向恢复的初始电压峰值。右图:漂移区的电子积累。
反向恢复模型
反向恢复教程基于参考文献1P256 的另一种器件模型近似建立。在参考文献中,假设在初始线性电流斜坡之后,器件突然变为由具有恒定振幅的电压驱动;这个示例使用软件的电路接口对带有反向二极管的电感负载进行建模,该二极管用于描述电流和电压的行为。
该电路包含两个并联的电压源,但在研究步骤中一次只激活一个。一个电压源用于导通状态,另一个用于转换过程。在电路接口中添加了一个全局方程节点,用于提高在使用因变量的时间导数定义变量时的数值稳定性,如下面的屏幕截图所示。
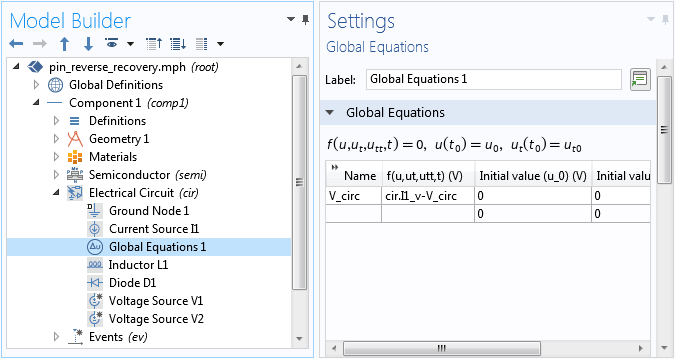
在电路接口中使用全局方程节点可以提高数值稳定性。
使用半导体接口模拟了了一个长度为 80 um 和 横截面积为 1 mm2的二极管模型,包括了 Fletcher 迁移率模型、Slotboom 带隙变窄和 Shockley-Read-Hall 复合等重要物理效应。要使迁移率模型生效,需要将半导体材料模型节点设置窗口中迁移率模型部分的下拉菜单设置为所需的迁移率模型(本例中为 Fletcher);否则,Fletcher 迁移率模型子节点无效。详请参见下面的屏幕截图。
![]()
必须在半导体材料模型节点中选择迁移模型才能使其生效。
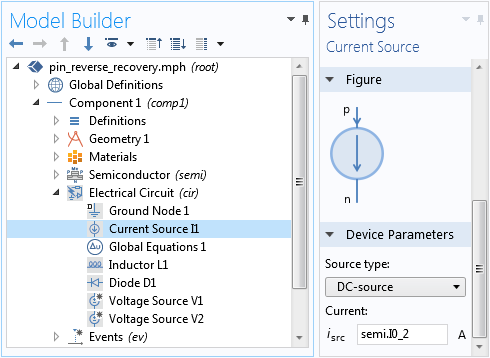
电路和半导体模型之间的双向耦合由电路中的电流源节点介导。流入电路的电流由半导体接口的终端电流指定。半导体金属触点的端电压又由电流源的电压指定。详请参阅下面的屏幕截图。
电路和半导体模型之间双向耦合的设置。
与正向恢复模型类似,事件接口用于标记施加电压斜率的突然变化。
设置瞬态反向恢复模型
如上所述,对于瞬态模型,选择正确的初始条件表示实际的物理系统至关重要。在反向恢复的情况下,初始条件应由开启状态给出。因此,在研究设置中,瞬态研究步骤(步骤 3)之前是一个稳态研究步骤,该步骤将施加的电压从零提升至开启状态 (Von) 下的稳态电压,如下面的屏幕截图所示。
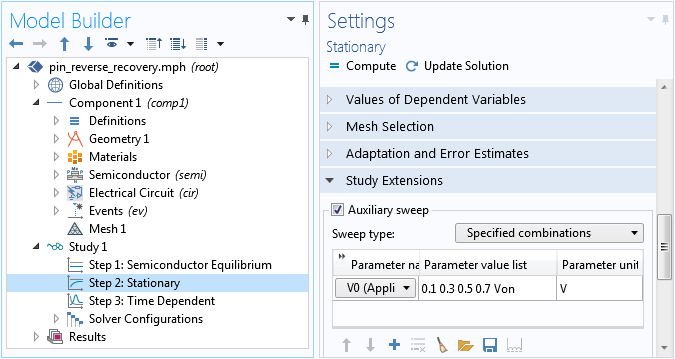
使用稳态研究步骤求解导通状态解,并将其作为瞬态研究步骤的正确初始条件。
半导体平衡研究步骤为稳态步骤提供了良好的初始条件。
与正向恢复教程类似,将瞬态步骤的相对容差设置为 1e-5 以获得更好的精度。此外,根据每个要求解的变量的数量级来手动缩放因变量。
PIN 二极管的反向恢复结果
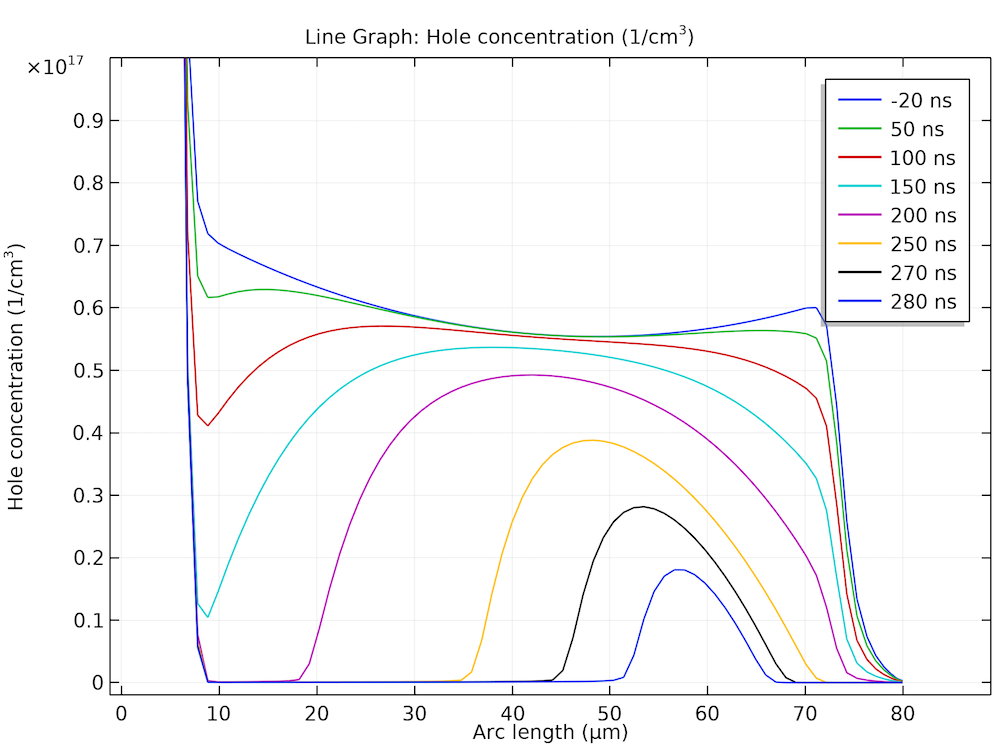
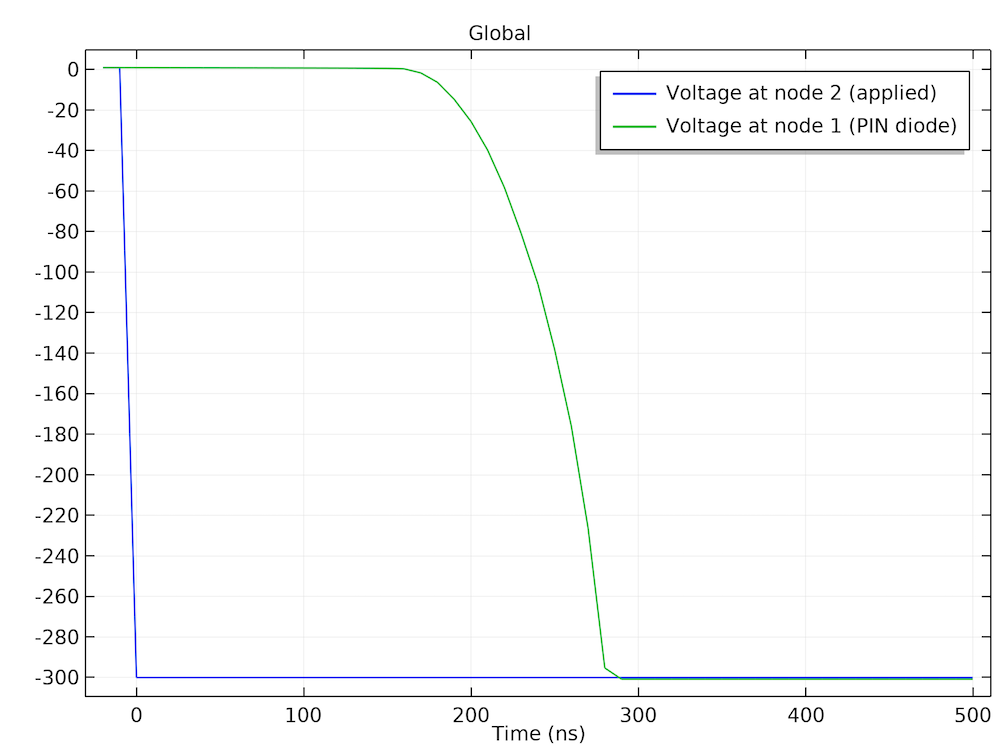
下图显示了几个选定时间点的空穴浓度分布、施加电压和器件电压的时间演变以及电流的时间演变。它们与电感负载和漂移区域中存储的电荷载流子的耗散预期行为一致。这些图与参考文献1中的图5.42、图5.43 和 图5.44 吻合良好。
左图:存储在漂移区的空穴损耗。中图:由于存储的载流子,二极管在施加电压转换后保持正向偏置一段时间。右图:转换后电流随时间的变化。
关于半导体载流子动力学分析的总结性思考
在这篇博文中,我们重点介绍了为瞬态模型选择合适的初始条件对正确描述物理系统的动态行为的重要性。我们还展示了使用软件的事件接口来标记时间演变中的突然变化,以及电路与半导体模型的双向耦合。同时还演示了如何在电路接口中使用迁移率模型和全局方程节点。欢迎您与我们分享您是如何在仿真中应用这些技术的。
如果您想自己动手尝试建立正向和反向恢复示例模型,请单击以下链接:
您还可以在 COMSOL 博客上了解有关半导体仿真的更多信息:
参考文献
- 1.B. Jayant Baliga,Fundamentals of Power Semiconductor Devices, Springer, 2008.





评论 (0)