如何求解经典的 CFD 基准问题：顶盖驱动空腔

顶盖驱动空腔是计算流体力学（CFD）领域用于验证计算方法的常用问题之一。虽然涉及的边界条件相对简单，但是流动特性却相当复杂有趣。在本文中，我们将展示如何在 COMSOL Multiphysics® 软件中定义这一基准问题，并演示映射网格划分和非线性递增等适用于多种 CFD 模型的技巧。

在 COMSOL Multiphysics® 中模拟顶盖驱动空腔

顶盖驱动空腔包含一个充满液体的方形空腔。在顶部边界处，切向速度被用来驱动空腔内的流体流动。剩余的三个壁被定义为无滑移边界条件，即速度为零。

为了确定基准模型，我们选择求解那些采用不同方法都能轻松解决的通用性问题。那么，该如何使用描述问题的最通用公式来比较不同的计算方法呢？一种方法是将方程式无量纲化，这意味着问题将不依赖于具体的材料、长度尺度或工作条件。对于顶盖驱动空腔内流体流动，我们可以求解无量纲纳维-斯托克斯方程。

在不包含体积力的情况下，不可压缩的稳态纳维-斯托克斯方程的形式为：

将速度（\textbf u^* = \frac
{\textbf u} {U}
）、压力（p^* = \frac
{p} {\rho U^2}
）和长度尺度（\textbf r^* = \frac
{\textbf r} {L}
, \nabla^*=L\nabla）无量纲化后，可将方程修改为下列形式：

雷诺数的定义是Re = \frac{\rho UL}{\mu}。此无量纲参数描述了流体的惯性力相对于粘性力的比重大小，详情可参考链接博客。

通过比较这两种方程形式，我们可以确定在求解无量纲化方程之前需要在COMSOL Multiphysics 模型中输入哪些参数。具体来讲，既然惯性项(\textbf u^* \cdot \nabla^* )\textbf u^*前面的系数为 1，因此我们在材料特性中设密度为 1。粘性项\nabla^{*2} \textbf u的系数是\frac{1} {Re}
，因此将它作为粘度输入。

应用非线性递增

随着雷诺数增大，与惯性项相比，粘性项在方程中的比重越来越低。由于粘性项在方程中是线性的，而惯性项是非线性的，因此雷诺数的增大使得问题越来越接近非线性。当求解非线性问题时，我们通常选择利用非线性递增方法为求解器提供良好的初始条件。下列博客详细讨论了非线性递增。

• 黏度递增方法提高 CFD 模型的收敛性
• 通过递增非线性改进非线性问题的收敛

在此模型中，我们在研究中对多个雷诺数进行辅助扫描。这样做有两个目的：

1. 将不同雷诺数的解与文献结果进行比较
2. 演示如何通过采用非线性递增方法来帮助求解

为了方便收敛，此例中的问题不需要非线性递增。不过如果处理高度非线性的问题，非线性递增是改进收敛性的一个重要技巧。

设置边界条件和约束

至于边界条件，顶壁朝x方向以U= 1 的速度移动。其他三个壁被施加了无滑移条件（U= 0）。

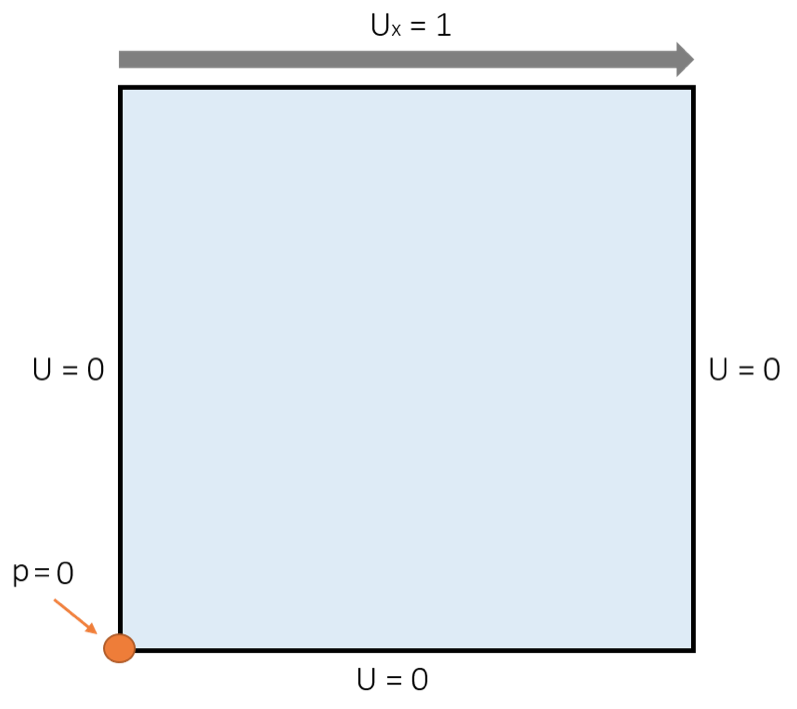
顶盖驱动空腔模型的边界条件。

尽管以上边界条件充分描述了待求解的物理问题，我们还需要对密闭的空腔施加另外一个必要条件：压力点约束。处于稳态的密闭系统中不存在具有明确压力水平的入口或出口。缺少了参考压力，纳维-斯托克斯方程对于稳态问题有无数个解，因为它们只能求解随压力梯度而变化的问题。因此，压力点约束规定了流体的绝对压力水平。当施加p= 0 的压力点约束时，这相当于 1 atm 的绝对压力，介绍如何指定流体压力的博客文章就这一点给出了解释。

只要求解密闭空腔内的稳态流，不管是搅拌釜式反应器还是自然对流问题，一定要在流体内远离流场关心区域施加压力点约束。使用压力点约束的示例模型有水杯中的自然对流和模块化搅拌器教程。

通过映射网格划分将域离散化

既然定义好了边界条件，接下来思考如何将求解域离散化。顶盖驱动空腔问题是演示如何借助映射网格高效且有效地对四边形几何进行离散化的完美示例。映射网格使用矩形单元进行域离散化。我们无需均匀分割这些单元。事实上，我们可以利用网格序列中的映射节点下的分布子节点沿边界定义单元之间的距离。在顶盖驱动腔体中，我们希望在流动梯度更高的地方，也就是无滑移壁附近堆叠更多单元，这样就可以在所有边上施加对称分布特征。

顶盖驱动空腔模型的映射网格。

此例中，我们对正方形划分了映射网格，事实上该技术可应用于任何四边几何结构。我们甚至可以将不规则的几何结构分割成多个四边实体，从而更方便地划分映射网格。一些情况下，映射网格比自由三角形网格的计算效率更高，而且更容易控制单元间距。与映射网格相关的案例，请参考平板上方的非等温湍流和管式反应器中的分解反应教程。

CFD 仿真结果与文献数据对比

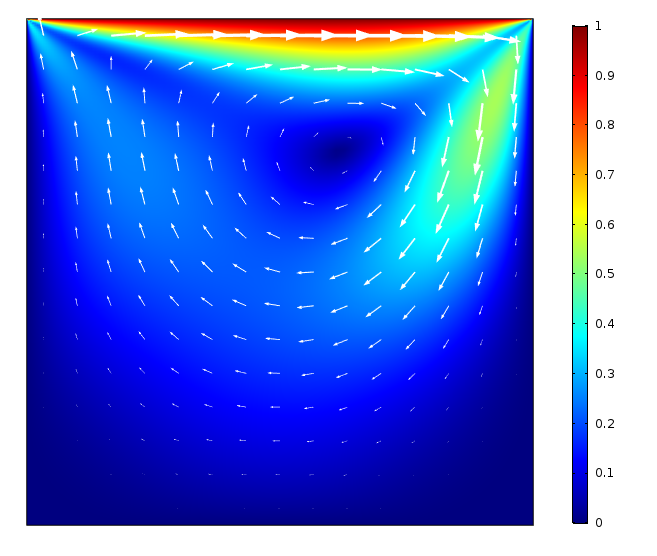
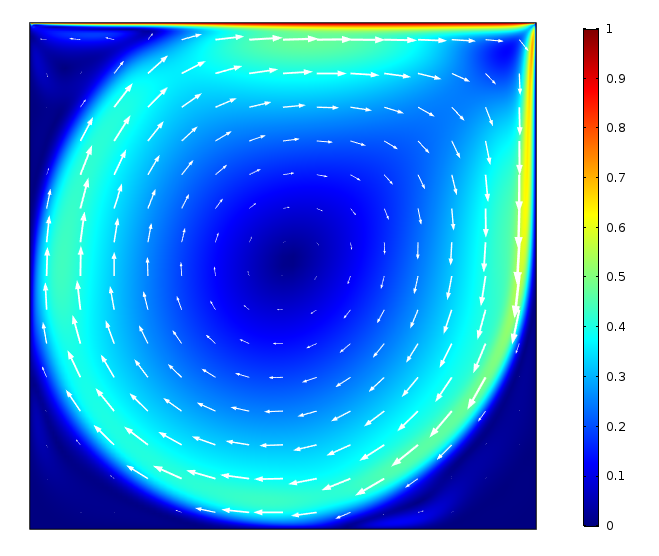
现在我们一起查看结果。首先是采用彩虹色表绘制的空腔内的速度大小，以及利用向量图指示的流动方向。可以看到，空腔顶部的速度接近于U= 1，此处的流体流动是由移动壁驱动的。流体被推向右侧的壁后，先向下流动，再回到腔体左侧。运动在空腔中心产生了一个大型涡流。图片显示，当雷诺数较低，例如等于 100 时（左图），由于粘性项较大而造成的能量损耗，空腔中心的速度较小。雷诺数增加到 10000 后（右图），空腔内的速度加快，涡流明显扩展到了空腔底部。

当雷诺数等于 100（左图）和 1000（右图）时，空腔内的流体速度和流动方向。

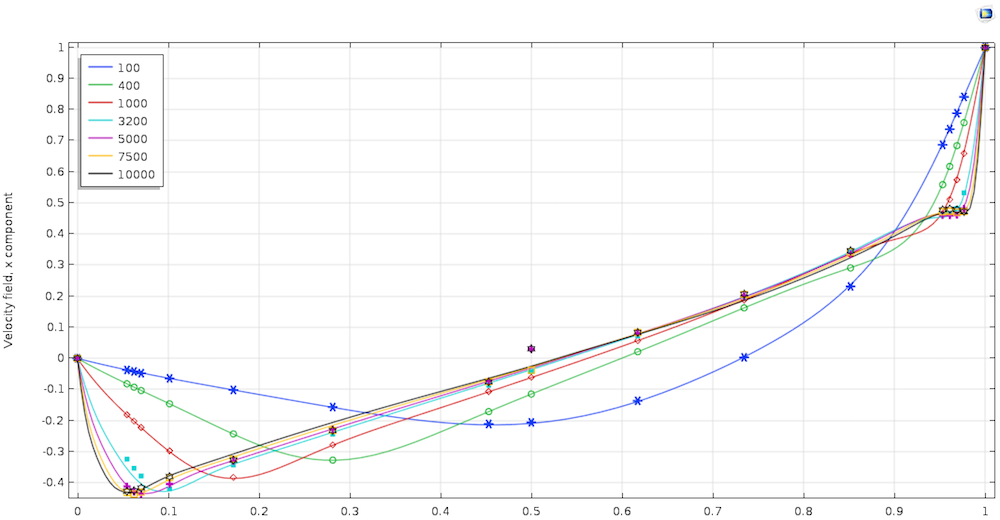
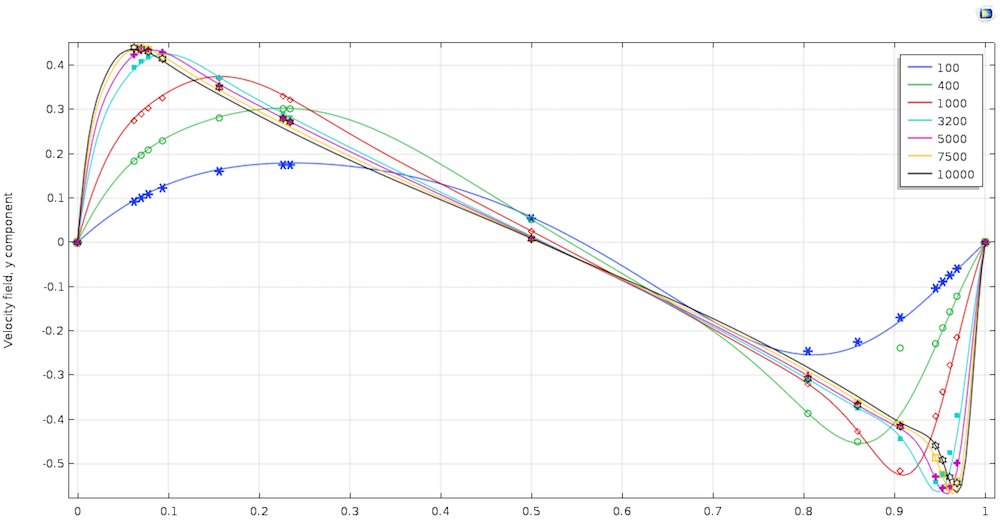
顶盖驱动腔是一个基准问题，因此我们需要参考现有文献（Ref. 1）进行比较。首先查看空腔中心线上的速度。下方左图沿垂直中心线绘制了速度（u）的x轴分量，右图为沿水平中心线的速度（v）的y轴分量。在这个雷诺数范围内，仿真结果与文献极为一致。

比较仿真结果与文献中，不同雷诺数下速度的x轴分量（左图）和y轴分量（右图）。

下方的速度绘图表明大型涡流形成于空腔的中心，但是空腔角落的流动情况又如何呢？我们利用流线绘制了空腔内各个区域的流动结构。由于仿真没有入口，我们将流线定位设为均匀密度（而不是在所选边界上）。

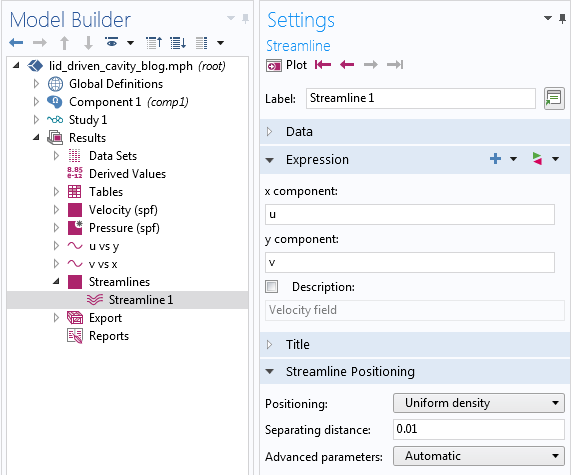
将流线定位设置为 均匀密度的设置窗口。

我们可以看到，对于较低的雷诺数，流体在左下角和右下角附近分离，并形成了两个涡流。随着雷诺数增大，流体的惯性增强，导致流动更早地与壁分离，并产生了更大的角速度。雷诺数进一步增大后，左上角形成了第三个涡流。对于最大的雷诺数（10000），除了左上角的涡流外，底部两个角落又产生了两个涡流。

不同雷诺数对应的空腔流动。

顶盖驱动空腔问题的结语

我们在本文中展示了如何定义经典的 CFD 问题——顶盖驱动空腔问题。辅助扫描改进了仿真的收敛性，使我们能够求解多个雷诺数。我们还演示了如何借助映射网格划分高效地对四边形几何离散化，并更好地对壁附近的流体的高梯度进行解析。此外，通过比较仿真结果与现有文献，我们确定了二者基本相同。

下一步工作

点击下方按钮进入“案例下载”页面，尝试亲手操作此案例。如果你拥有COMSOLAccess 账号和有效的软件许可证，可以下载模型文档和相关的 MPH 文件。

参考文献

1. U. Ghia, K.N. Ghia, and C.T. Shin, “High-Re Solutions for Incompressible Flow Using the Navier-Stokes Equations and a Multigrid Method,”Journal of Computational Physics,vol. 48, pp. 387–411, 1982.