
使用湍流模型准确地模拟湍流始终是一个挑战,因为模型本身就涉及到简化问题。此外,准确的模型往往会增加一些方程,而这些方程对已经高度非线性的模型的收敛性没有帮助。为了解决这个问题,COMSOL Multiphysics® 软件 5.3 版本中引入了v2-f 湍流模型。它结合了描述湍流边界层各向异性的模型所具有的准确性与两方程湍流模型的鲁棒性。
用 v2-f 湍流模型进行 CFD 建模
在湍流边界层中,边界处的法向动量传递受到固体壁面的强烈抑制。另外,靠近固体壁面处的湍流强度的法向分量比平面分量受到更强烈地抑制。这意味着在壁面法线方向上的质量和热量传递也被部分地阻断。传统上,这种阻挡效应是通过在壁求解的湍流模型中对湍流黏度的法向分量引入阻尼函数来处理的。
Durbin 通过直接的数值模拟,证实了涡流黏度的近壁阻尼是由湍流强度的法向分量的抑制引起的,其关系如下:
(1)
其中,Cμ 代表一个模型常数,\overline v^2 是湍流速度的法向分量的方差,T 代表湍流时间尺度。
壁对湍流强度阻尼的影响在下图中进行了描述。从气泡或薄片形状的物体表面到其中心的距离代表了气泡或薄片形状的中心点的湍流强度的平均值。
在靠近壁的地方,速度的波动在 x 方向和 y 方向比 z 方向大得多。速度波动是各向异性的,表面呈现出薄片的形状。离壁更远的地方,在 x、y、z 三个维度上的波动幅度相同,速度波动是各向同性的,表面呈现出球形气泡的形状。气泡和薄片形状的相对大小代表了不同方向上的波动涡流的相对大小。
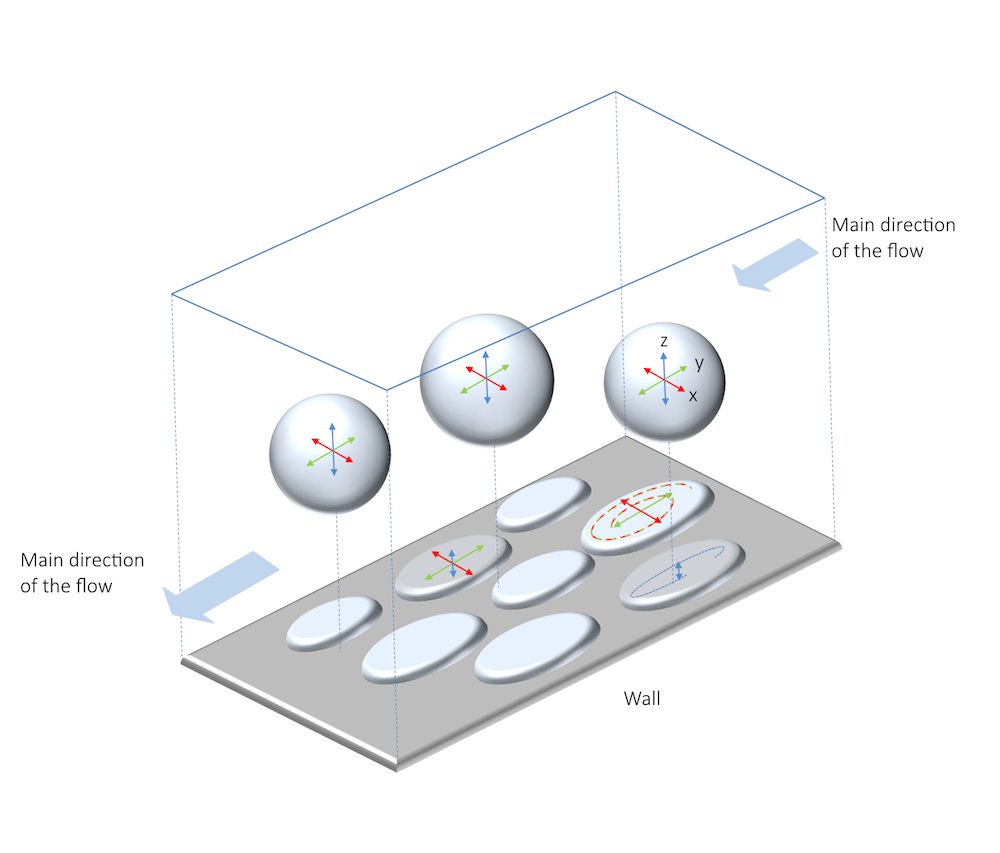
将平均速度波动表示为假想的气泡或薄片形状。从表面到气泡或薄片中心的距离代表湍流强度的平均大小。
v2-f 湍流模型描述了湍流边界层中湍流强度的各向异性,除了湍流动能和耗散率的两个方程外,还使用了两个新方程。CFD 模块是 COMSOL Multiphysics 的附加产品,它的实现是基于 F. Billard, J. Uribe 和 D. Laurence 在他们 2008 年的论文中的表述。
v2-f 湍流模型的方程式
为了准确描述湍流能量的传输和湍流能量在不同方向的再分配,v2-f 模型引入了两个新方程。第一个方程用一个等于 \[{{\overline {{v^2}} } \mathord{\left/ {\vphantom {{\overline {{v^2}} } k}} \right. \kern-\nulldelimiterspace} k}\] (在科学文献中通常表示为 φ 或 ς)的变量来描述湍流向壁面的法向传输。在这个方程中,\overline {v^2} 表示湍流速度的法向分量的方差,k 表示湍流动能。
第二个方程是混合系数的椭圆偏微分方程(科学文献中通常表示为 α)。椭圆混合方程考虑了非局部效应,如壁引起的湍流动能在法线和平行方向上再分配的阻尼。由于独立变量的名称,这个模型通常被称为 v2-f 湍流模型的 φ-α 版本。该模型与标准的各向同性湍流模型同样稳健,与原始的、低稳健的 v2-f 模型的表述一样准确。
示例1:周期性山丘基准案例
CFD 模块的实现已经用一些基准案例进行了验证,包括周期性山丘基准案例。在这个模型中,水流被迫通过两个平行的山丘,在两个垂直的入口和出口边界上,速度场是周期性的(如下图所示)。这意味着,虽然从入口到出口边界有一个压降,但它们的速度场是相同的。
在下图中,流向是由左至右的。我们可以看到,在流动方向的山丘后面,形成了一个脱离流动的再循环区。再循环区的大小以及从入口到水流重新附着的距离本身就很难用 RANS 湍流模型来预测。使用 CFD 模块得到的结果与科学文献中报道的结果非常一致。
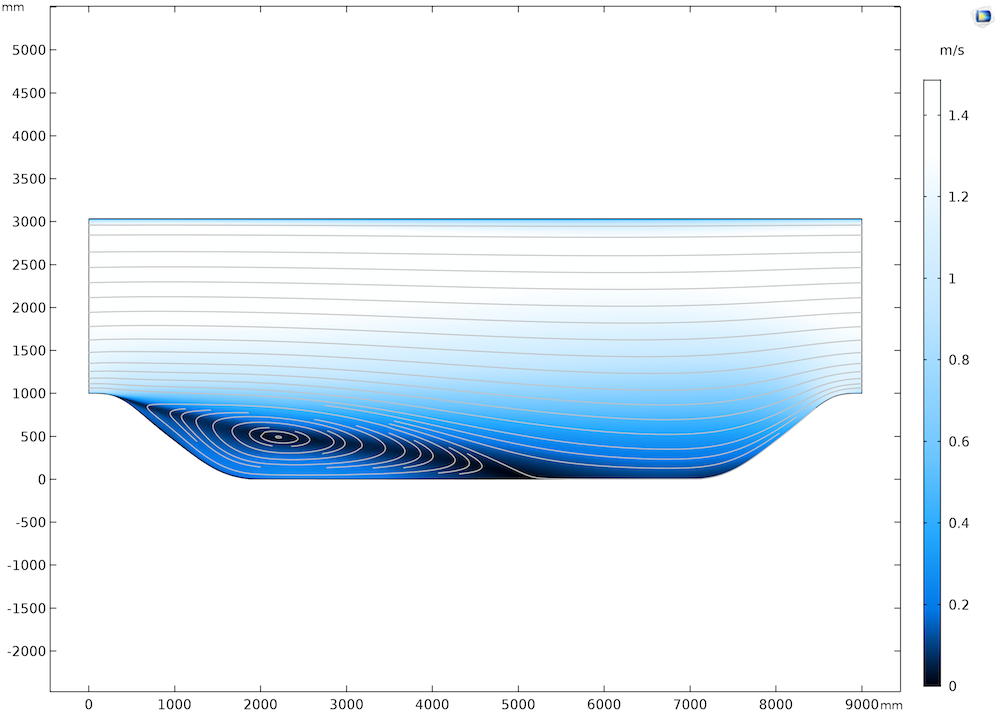
流过两座山的流动,在两座山上方的垂直边界上,入口和出口边界的速度曲线是相同的。流动是从左到右的。
示例2: 水力旋流器中的流动
另一个有意思的问题是有两个切向入口的水力旋流器中的流动。两个出口分别位于顶部和底部。来自底部的水流通常包含不受欢迎的颗粒,因此它被称为废弃流。顶部的出口流被称为接受流。困难在于捕捉半自由涡流,这对于标准的二方程模型来说是无法实现的。
有关模拟水力旋流器模中的更多信息,请参阅这篇阅研究论文。
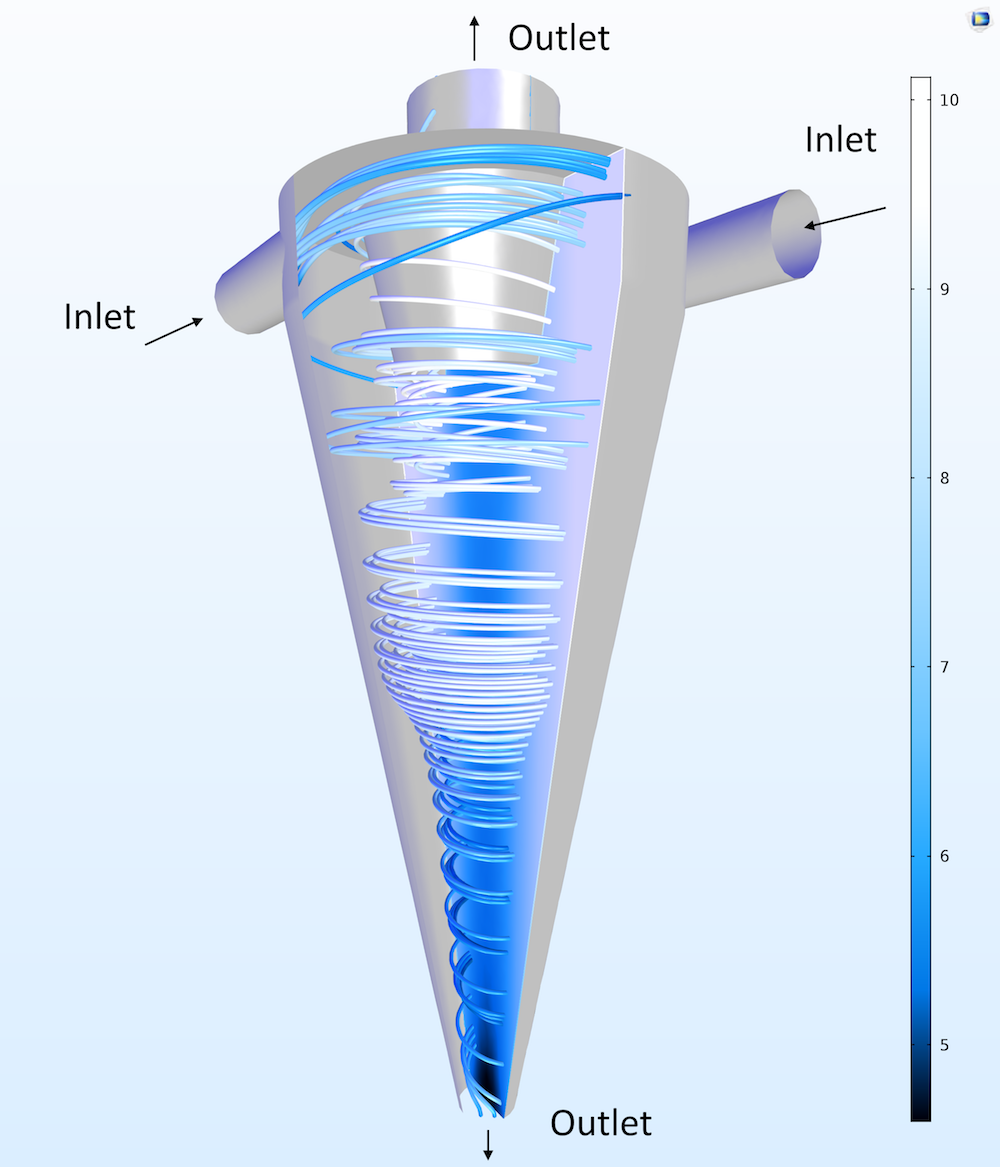
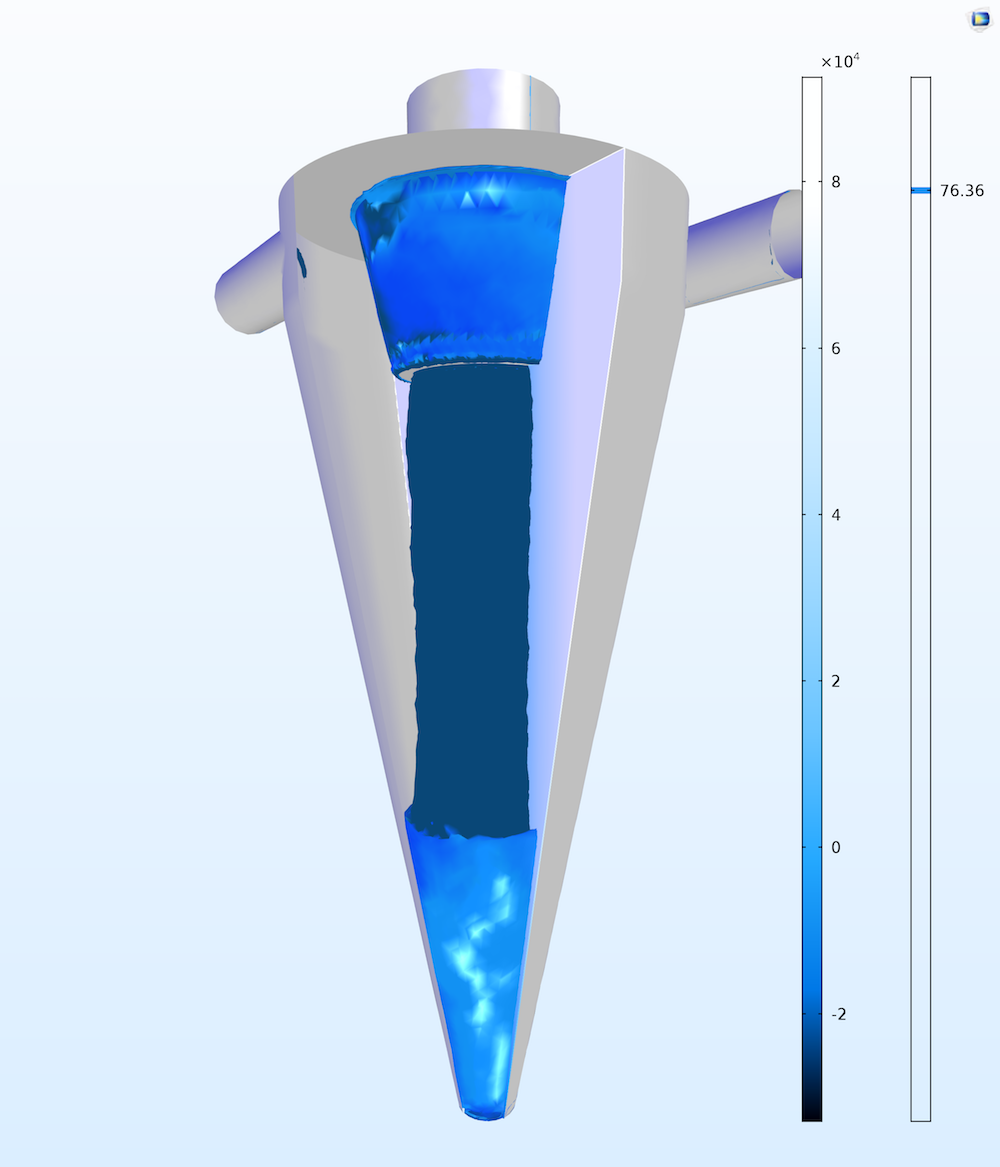
左图:水力旋流器中的速度场(流线)和压力场(断面图)。右图:旋流器中涡度的绝对值和压力截面的等值面。仿真模拟了旋流器中心的自由涡流。
下图显示了在顶部出口下方的速度方位角分量。在出口管道外侧的径向位置出现最大值的剖面图,与科学文献中报道的解非常一致。此外,沿半径方向远离最大值的方位角速度的下降也与文献的结果吻合。
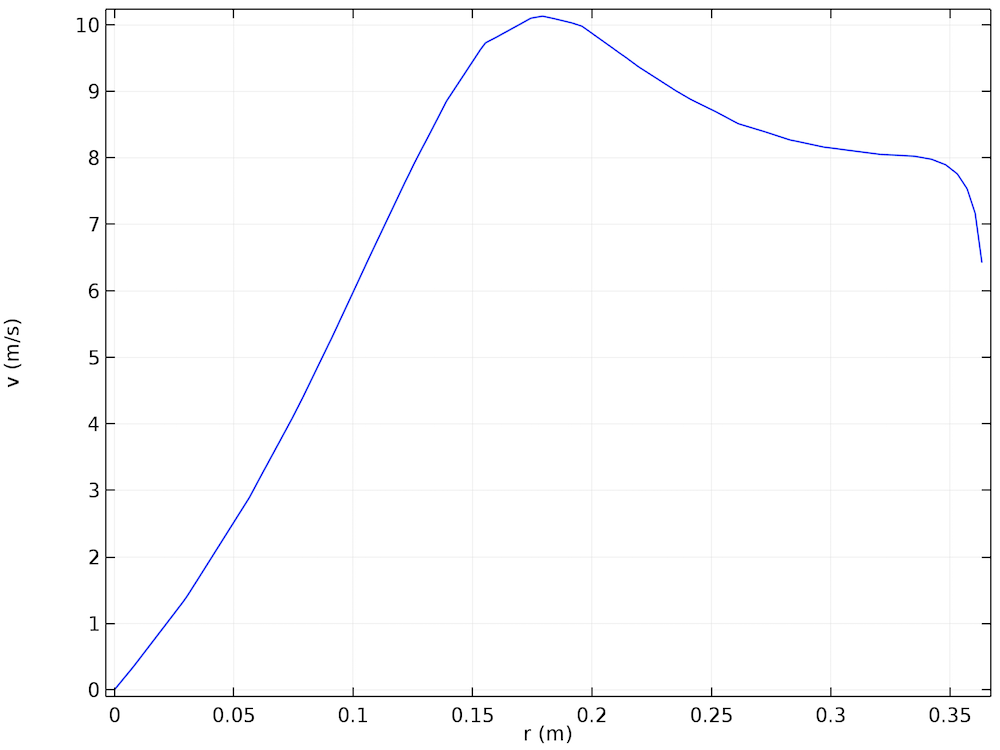
速度的方位分量与旋风顶部水平出口下方半径的函数关系。
总而言之,新的 v2-f 湍流模型扩大了 CFD 模块的适用性,包括需要模拟各向异性湍流的情况。该模型给出了两方程模型不可能获得的精度,但它与标准的两方程模型一样稳健。
其他 CFD 资源
- 自己动手尝试:获取水力旋流器中的流动教程模型
- 在发布亮点页面上了解更多关于 CFD 模块的更新信息



评论 (0)