在 COMSOL Multiphysics 中执行弱形式

这篇博客是弱形式系列博客的组成部分，旨在帮助用户在最小的先决条件下理解弱形式。在第一篇博客中，我们学习了弱形式的基本概念。所有方程停留在解析形式。今天我们将使用 COMSOL Multiphysics 仿真软件来从数值上求解上述方程。我们在此强烈建议您打开 COMSOL 软件，随我们一起操作。

重述基本思想

在之前的介绍中，我们研究了一个简单的无热源一维稳态传热示例，其中温度T是在1\le x\le 5的域内区间内定义的关于位置x的函数。

弱形式使用试函数\tilde{T}(x)作为被积函数的局部采样函数对解进行约束并求积分，从而将传热物理场的微分方程转化为积分方程。对弱形式分部积分以降低求导阶数，从而更利于数值计算。同时还提供了一种非常自然的方法来通过热通量指定边界条件。对于以温度表示的固定边界条件，弱形式还是利用试函数和自然边界条件，在方程组中构建对应的附加项。

最后，我们得到如下的示范方程：

(1)

其中左侧的积分只涉及温度的一阶导数，右侧的第一项将左端 (x=1) 的向外通量定义为 2，右侧的另外两项共同指定了右端 (x=5) 处的温度为 9。

弱形式偏微分方程接口

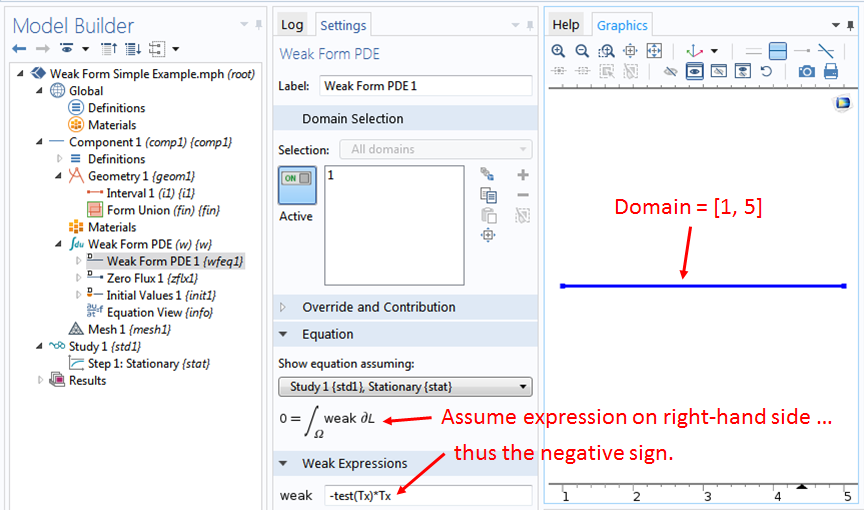
在 COMSOL Multiphysics 中执行方程(1)，需在模型向导中创建一个一维模型，并选择弱解型偏微分方程(w)接口（数学>偏微分方程接口）和稳态研究。因变量可设为T，表示我们方程中的待求解变量。对于几何，通过一个从 1 到 5 的间隔建立，缺省”弱解型偏微分方程 1″节点下的弱表达式为：-test(Tx)*Tx+1[m^-2]*test(T)，其中第一项对应方程(1)中的被积函数，第二项对应热源，我们的简单示例不包含这一项，所以需要从输入栏中移除。

新的弱表达式如下：-test(Tx)*Tx，其中Tx是 COMSOL Multiphysics 温度的一阶导数\partial_x T(x)，test(Tx)是试函数的一阶导数\partial_x \tilde{T}(x)。负号是因为 COMSOL 中约定输入框中的表达式在等号（如设定窗口的“方程”栏所示）右侧，而上述我们推导的方程(1)中的积分则在等号左侧。

弱贡献特征

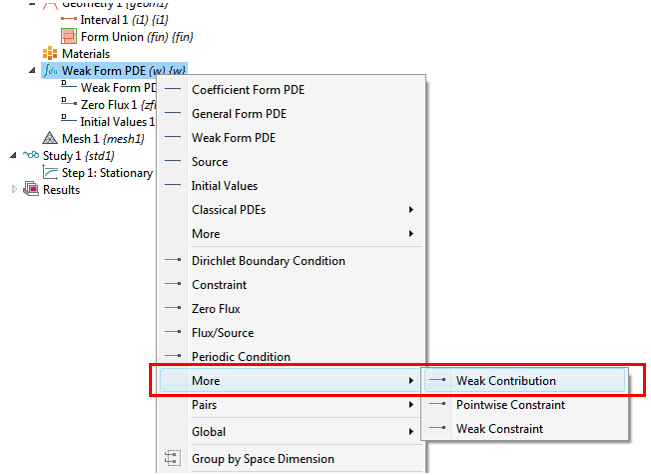
右击弱解型偏微分方程(w)节点，利用弱形式项来定义方程(1)右侧的边界条件。我们可以看到内置了诸如狄氏边界条件等边界特征，为方便用户访问，它们都被收录在弹出菜单中。因为我们对自定义方程很感兴趣，因此将鼠标移至弹出菜单中的更多项，并在接下来的弹出菜单中点击弱贡献。

在”弱贡献1″节点设定窗口的边界选择栏，在域（x=1）的左端选择边界 1，在设定窗口的弱贡献栏输入弱表达式：-2*test(T)。此步骤定义了方程(1)右端的第一项，指定边界x=1处的向外通量为 2。

固定边界条件

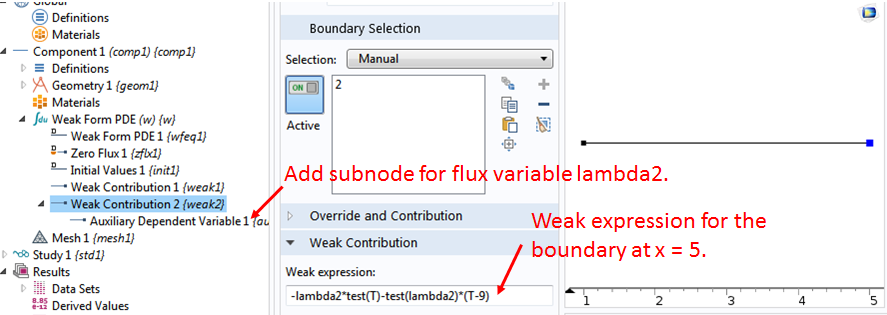
对于x=5处的固定边界条件，即方程(1)右侧的后两项所定义的T=9，我们在边界 2 处增加另一个”弱贡献”节点，并在其下建立一个助因变量子节点。

输入lambda2作为子节点中场变量的名称，然后输入弱表达式作为方程(1)中的后两项：-lambda2*test(T)-test(lambda2)*(T-9)

离散

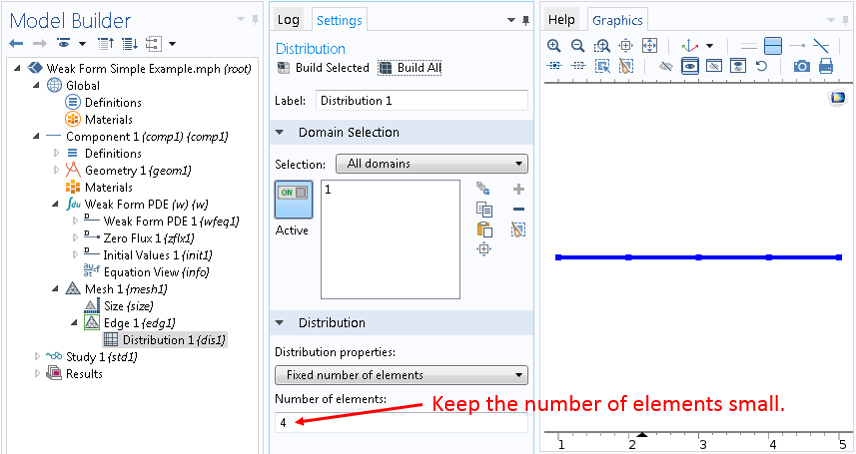
COMSOL 软件通过创建网格对域进行离散。右击网格 1节点选择边，然后右击边 1并选择分布。然后将”单元数”设为 4 并点击全部构建。我们有意将单元数控制在较小的值，以便之后能更详细地讨论离散。

在弱解型偏微分方程(w)节点设定窗口中的离散栏，将”单元阶次”设为线性（点击模型开发器下的显示按钮，在弹出菜单中选择离散化离散化栏）：

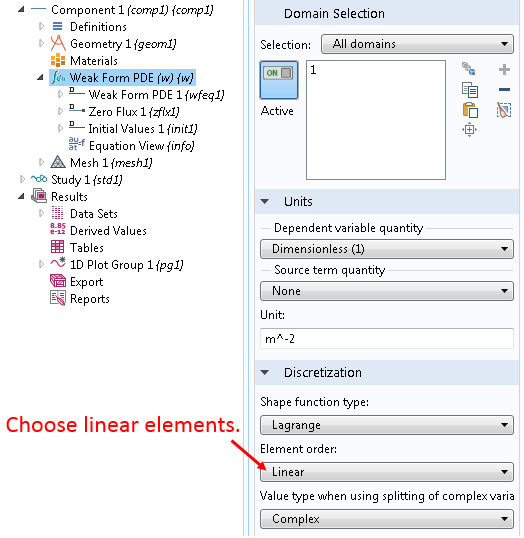
使用 COMSOL Multiphysics 计算解

现在我们可以点击计算来检查解是否合理。

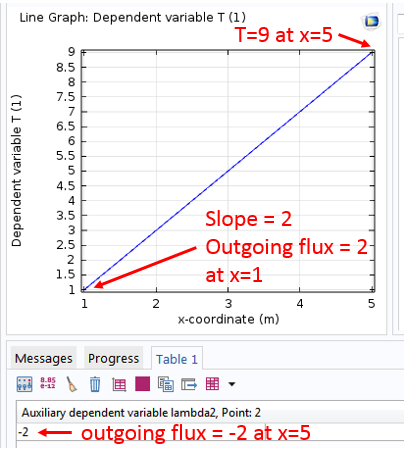
解表示为域内的一条直线，这与稳态无热源的温度场分布一致。直线的斜率为 2，这和边界条件x=1处的向外通量为 2 一致。x=5处的温度为 9，符合固定边界条件的指定。因为没有热源，流出域的总热通量在稳态时的和应为零。因此，x=5处的向外通量应为 -2。

我们可以轻松通过对热通量变量lambda2进行点求值来验证该过程，如下图所示：

一些读者可能会疑惑是否每次都需要求解助变量lambda2，即我们所称的拉格朗日乘子，尤其是在建模者并不需要时，而且求解该变量必然还需要更多计算资源。我们将在后续的博客中介绍 COMSOL Multiphysics 提供的其他特征，允许用户决定是否需要求解拉格朗日乘子。

总结及下一篇博客

今天我们重温了弱形式的概念并在 COMSOL Multiphysics 中执行了一个弱形式方程示例(1)。利用简单物理参数得出的数值解与预期一致。

在未来的博客中，我们会从”内部”观察类似方程(1)的弱形式是如何被离散和数值求解的。我们还将看到如何通过不同的方式对这一问题求解，以及如何为不同种类的问题设定不同的边界条件。

敬请期待！