
在上一篇博客中,我们讨论了时间和空间的积分方法,了解了如何使用积分耦合算子计算反导数。今天,我们将进一步扩展这个想法,介绍如何分析变化极限的空间积分,无论它们是显式指定还是隐式定义。这个技术对分析结果以及在 COMSOL Multiphysics®软件中求解积分和微分方程都有帮助。
积分的变化极限
在 COMSOL Multiphysics 中,我们可以通过使用积分组件耦合算子或结果部分派生值下的积分工具来计算空间积分。虽然这些积分总是在一个固定的区域内进行计算,但有时我们会想改变积分的极限,并获得与新极限有关的结果。
例如,在一个一维问题中,积分算子通常会作如下计算:
其中,a和b是域中的两个端点,代表积分上下限。
不过,我们要做的是,计算出:
并得到关于积分s的可变极限的结果。
由于积分算子在一个固定的域内工作,我们来考虑如何使用它们来获得变化极限的积分。一个小窍门就是通过与一个在积分极限内等于1、在极限外等于0的函数相乘来改变积分值。也就是说,定义一个核函数
\begin{cases}
1 \quad x \leq s\\
0 \quad \mathrm{otherwise},
\end{cases}
并计算
就像我们在上一篇关于时间和空间的积分方法的博客中所指出的,我们可以通过使用逻辑表达式或阶跃函数来建立这个核函数。
我们还需要知道在 COMSOL Multiphysics 中是如何指定辅助变量s的。这就是dest算子发挥作用的地方。dest算子强制其参数在目的点上而不是在源点上被计算。在这个例子中,如果我们在 COMSOL 软件中把上述方程的左边定义为一个变量,那么我们就在右边输入dest(x)而不是s。
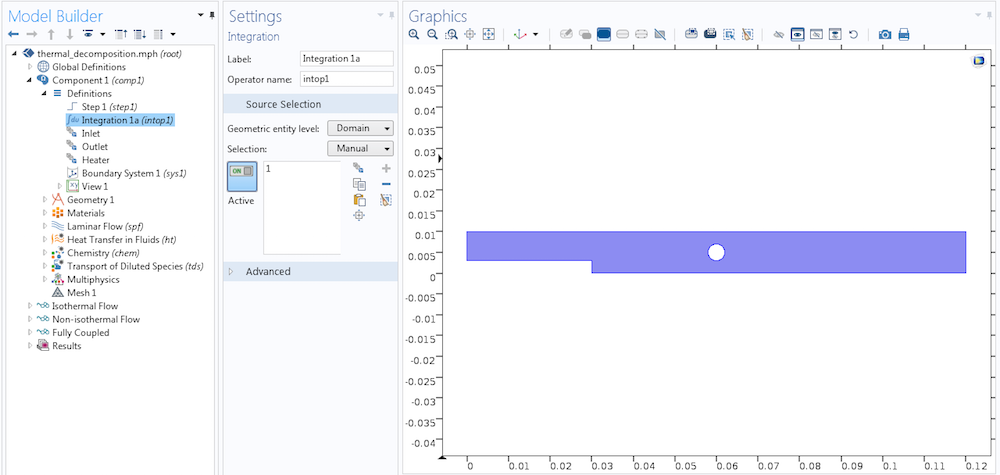
我们用一个例子来证明这一点。例如,一个模拟了一个平行板反应器中的稳态放热反应的模型。在中心附近有一个加热筒,左边有一个入口,在x= 0 处。其中一个化合物的浓度为cA。
我们要做的是计算进气口和与进气口距离为s的横截面之间每单位厚度的总摩尔数。然后,将结果与进气口的距离作对比。
首先,我们为整个域定义一个积分耦合算子,保留默认的积分算子名称为intop1。如果我们评估intop1(cA),就可以得到整个域的积分。为了水平地改变积分的极限,我们用一个阶跃函数建立一个核,我们把它称作step1。然后,我们定义一个新的变量,intUpTox。
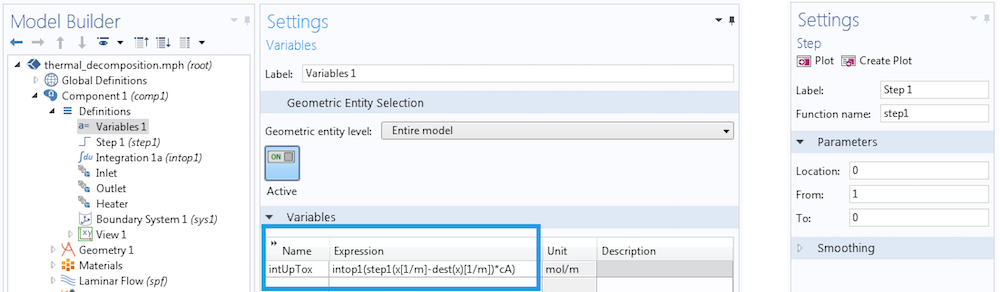
结合积分耦合算子、dest算子和新变量来计算具有变化极限的积分。
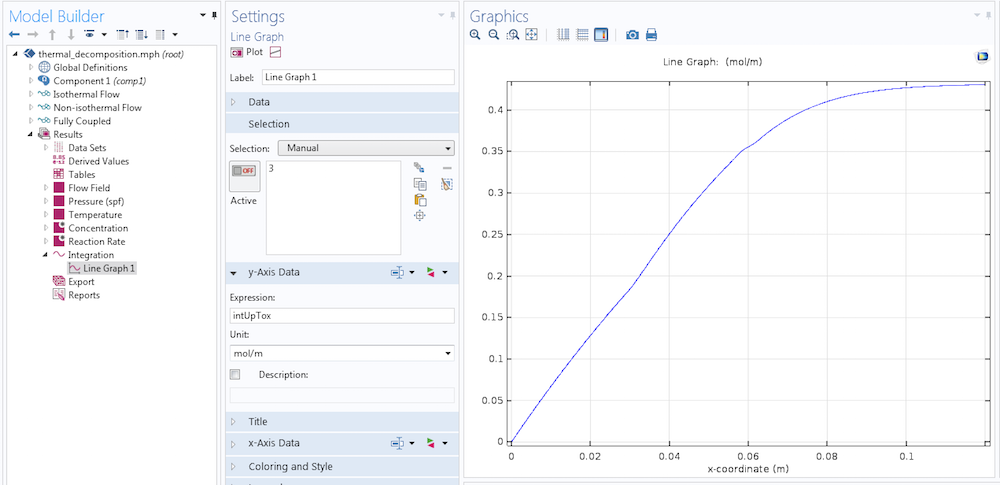
我们来看看上图中描述的变量是如何工作的。作为一个变量,它是一个分布式的量,其值等于积分算子返回的值。在积分过程中,我们在积分域的每一个点上计算x,只在计算intUpTox的点上计算dest(x)。我们找到一条水平线,从入口处一直延伸到出口处,并绘制intUpTox。
如果我们改成绘制intUpTox/intop1(cA)*100,就会得到一个给定点左边的百分数质量与x坐标的关系图。
在上述积分中,积分的极限是以x坐标为单位明确给出的。但有时,极限可能只以隐式标准给出,而反转这种标准并获得显式极限可能并不直接。例如,假设我们想知道在离加热缸中心一定径向距离内的总摩尔的百分比。给定从缸中心(xpos,ypos)的距离s,我们希望核函数在径向距离内等于1,在其外等于 0。要做到这一点,我们可以使用:
但我们如何指定s呢? 再次使用dest算子s^2 = (\mathrm{dest}(x)-x_{pos})^2+(\mathrm{dest}(y)-y_{pos})^2,带入等式得到:

通过定义一个截线数据集来实现这个方法,用于获得通过孔中心的水平线,并将我们的积分表达式的图形置于其上。截线 不一定是水平的,它只需要穿越积分算子定义的整个域。此外,s应该在截线上单调地变化。
在下面的图片中,我们通过放大图表的左下角区域添加了一个函数这一部分显示,在距离加热孔中心不到 2 mm 的地方,绘图上没有结果。这是因为该区域不在我们的计算域内。由于孔的半径为 2 mm ,所以在 2 mm 的标点上,序数从 0 开始。
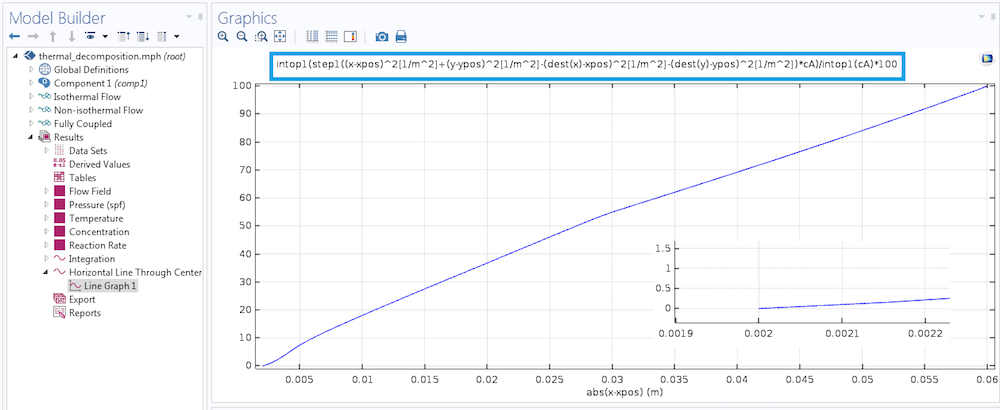
一个域中的质量百分比,在固定点的径向距离内。径向距离是通过使用隐式表达式中的dest算子来改变的。
积分和积分微分方程
在前面的小节中,我们在给出积分的情况下对积分进行了计算。但是,如果我们有了积分并想求解积分,该怎么处理?这种问题的一个例子是 Fredholm 第一类方程
当给定函数g和核K时,我们要求解函数u。这些类型的积分方程经常出现在反问题中。
在整数微分方程中,未知函数的积分和导数都会涉及。例如,假设我们有
并且对于给定的所有其他函数,想要求解u。
在 COMSOL 案例库中,有以下整数偏微分方程:
其中,求解温度T(x),并给出所有其他函数和参数。
我们可以使用固体传热接口来解决上述问题。在这个接口中,将上述方程的右侧添加为随温度变化的热源。第一个源项是可直接求解的,但我们需要使用积分耦合算子和dest算子在第二项中添加积分。对于名为intop1的积分算子,我们可以使用intop1(k(dest(x),x)*T^4)计算
关于这个问题的实现和物理背景的更多细节,您可以点击这里下载整数-偏微分方程教程模型。请注意,一些积分方程往往是奇异的,我们需要使用正则化来获得解。
不同极限的空间积分总结
在今天的博客中,我们学会了如何在不同的空间极限上进行积分。这对于在后处理中计算积分或定义积分和微分方程是必要的。想要了解更多信息,请浏览以下 COMSOL 博客的相关内容。
关于积分和其算符的子完整列表,请参考 COMSOL 参考手册。
如果您对文中讨论的技术或对您的 COMSOL Multiphysics 模型有疑问,请随时与我们联系。




评论 (0)