双电容悖论问题中的电容和电感存在吗？

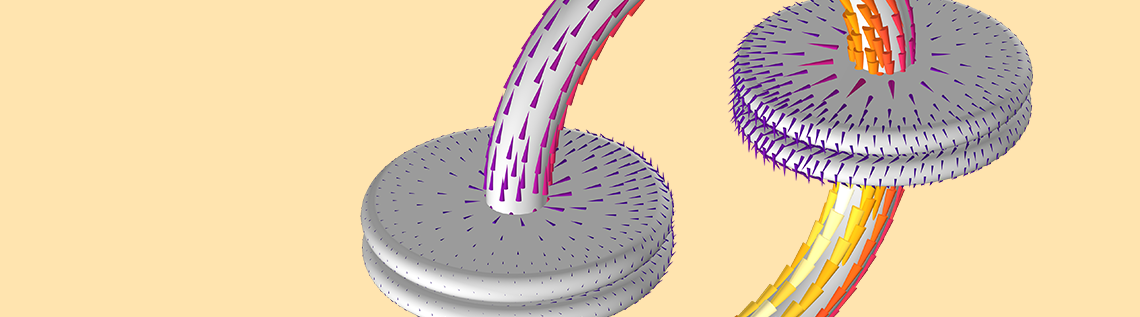
双电容悖论是一个具有启发性的思想实验，旨在揭示电路模拟的一些局限性，并且已有许多不同的方法可以求解这个问题。我将在 COMSOL Multiphysics^®中添加一个可以用软件求解的方法，然后对其进行扩展，提出并回答一个具有更大启发性的问题：电容和电感存在吗？让我们来深入探讨！

双电容悖论

这个思想实验通常描述如下：考虑一个装置，由两个电容为C的等效电容器组成，二者中间并连了一个打开的开关。所有的导线和电容器都是由理想的、完全无电阻无损耗的材料制成。其中一个电容器的电位为V_i，因此存储的电荷为Q = CV_i。另一个电容器上没有电位差，因此没有存储的电荷。关闭开关后会发生什么？

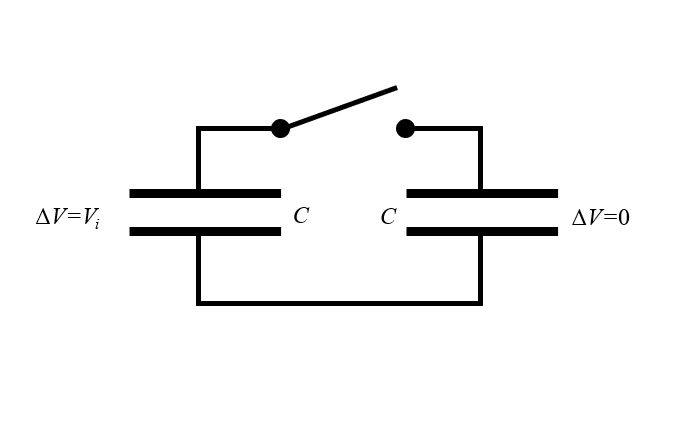
双电容器悖论的示意图。电容器的两个电极板之间存在电位差。开关闭合时会出现什么情况？

有些人在介绍这个思想实验时会抛出一个“障眼法”，认为第一个电容器上的电荷会流入第二个电容器，从而使第一个电容器上的电势差减小，第二个电容器上的电势差增大，直到达到稳定状态 —两个电容器上的电势差相同，均为V_i的一半，因为相同的电荷Q分布在两个等效的电容器上。但是，这将立即导致一个悖论，因为每个电容器中的能量都是W_C = \frac{1}{2} C \Delta V^2。如果初始能量是 ，最终能量是2 \frac{1}{2} C\left( V_i/2 \right)^2=\frac{1}{4} C V_i^2，那么另一半能量去哪里了？

从量子力学到热力学，有很多求解的方法。从教学的角度来看，这些解可能都是有效的。然而，其中许多都隐含了实际条件，即电线和电容器必须有一定的电阻或电感。但为什么呢？至少在思想实验中，假设材料完全无损耗，忽略电阻是合理的。那么电感呢？在这个思想实验中，我们可以忽略电感吗？让我们跟随这个问题，看看它是否能给出一个有趣的答案……

一个关于该悖论的简单解

我们的设备由两个理想的无损电容器组成。但即使是理想电容器，也必然使空间上的电荷发生分离。也就是说，电容器必须有一定的尺寸。如果每个电容器都有尺寸，那么它就必须与另一个电容器保持一定的非零距离。因此，如果我们稍微重画一下上述示意图，就会发现有两个电容器和两个有限直径的无损耗导线半环，随时间变化的电流可以沿导线流动。但我们怎么称呼这样的结构呢？电感器！

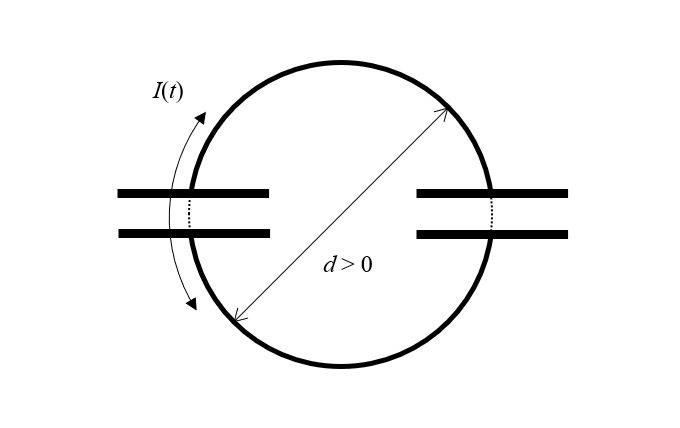
要解决这一悖论，必须认识到，该结构的尺寸必须不为零，电流将绕一个面积有限的环流动，因此它也是一个电感器。

这里绘制的结构必须具有有限的尺寸，只要这个结构存在于在自由空间具有磁导率的宇宙中，那么这个结构也必须具有电感。因此，只要我们的电路中有一个电容器，那么电路中也一定有一个电感器。事实上，情况会变得更好：如果有一个电感器，即使是一个无损耗的电感器，流过它的任何随时间变化的电流都会在电感器的匝之间产生一个电场，因此我们添加到电路中的任何电感器都会起到电容器的作用！我们可以无限地沿着这个逻辑思路推演下去，但在这里，只需用一个电感L来修改电路就足够了。

现在，我们有了一个LC电路，它的解析解可以立即消除悖论：电流将在电容器之间和有限长度的导线上来回流动，振荡频率为：f=1/(2\pi\sqrt{LC})。永远不会有稳态解，因此永远无法单独评估静电能。我们还必须考虑电荷运动所产生的能量，即电流的流动，I，其值可以由W_L = \frac{1}{2} L I^2获得。电能和磁能的总和 (\frac{1}{2} L I^2 + \frac{1}{2} C V^2) 不会随时间而改变。

在 COMSOL Multiphysics^®软件中进行验证

使用 COMSOL Multiphysics^®和 RF 模块可以直接建立一个模型来验证这种情况。使用电磁波、瞬态接口和静电接口来计算初始条件。我们将模拟一小块完全真空的区域，其中包含电容器和导线。电容器板、导线和体积周围的空间都被视为完美导体，即电磁场不会穿透任何边界。COMSOL 学习中心文章： “电容放电模拟”中提供了建立此类电容放电模型的指南。

对这一时域模型进行求解并对总电能和总磁能进行评估，结果显示出预期的振荡行为。还可以将模拟域划分为不同的区域，以评估两个电容器周围区域以及周围空间的总能量。下图显示了能量在空间和时间上的振荡情况。

动画显示了电容器板和导线表面的电流以及两者之间空间的磁场。

总电能和总磁能会随着时间的推移而振荡；在这种无损装置中，电能和磁能的总和不会发生变化。

不同域中的电能和磁能的总和显示能量在时间和空间上的振荡。

由上图可以观察到，这些曲线图在时间上并非纯正弦曲线。高频内容，即随时间变化的能量波纹来自哪里？它们来自结构。很明显，两块电极板具有明确的电容，但由于导线的存在，电荷也会分离，而且整个结构位于一个具有谐振频率的圆柱形空腔内。该设备的所有这些不同部分都对电磁行为有一定的影响。每个部分的贡献可能都很小，但当考虑一个有限大小的结构时，它总是存在的。

电容和电感存在吗？

现在是时候对这个（或任何其他）电磁装置提出一个更具挑战性的问题了：它有电容和电感吗？我们已经清楚地看到，这个特殊的装置同时具有电容和电感。但是，如果我们在电容器极板之间添加一种非常强的介电材料，对它进行改装会怎样呢？这将使电容大大增加，但电感不变。如果把电容做得更大，是否可以说电感无关紧要呢？

简单的回答是：不，我们永远不应该认为一个电动装置是纯电容式或纯电感式的。在电动装置中，电荷的空间分离总会产生电能，电荷的运动总会产生磁能。虽然我们有时可以假设忽略其中一种情况，但始终要记住，这只是在思维上进行了简化。

此外，所有实际材料都有一定的有限电阻，因此，为了更符合实际，应该把所有东西都说成是有阻抗的，而这就是我们有时会陷入更大麻烦的地方。在处理频域模型时，电气设备的阻抗可以用以下我们非常熟悉的表达式来计算：

在这个表达式中，电阻R用于衡量移动电荷的动能，即电流如何转化为热能的量度。

这个方程一看就知道与单自由度阻尼谐振子有关，而谐振子是工程学和物理学中研究最深入的问题之一。我们知道，从这个表达式中可以计算出振荡器的谐振频率和品质因子，并且现实中的设备都具有基本谐振和品质因子。这使我们想把上述两者等同起来，并试图将现实世界中有限大小的电气设备简化为单一的电阻、电容和电感。这是一个概念上的错误，而且永远不会成立，因为上述阻抗表达式只适用于具有无限小尺寸的设备。

任何实际设备都具有有限尺寸大小。设备在共振时，电能和磁能在空间和时间上都会发生变化，正如我们从上面的图中看到的那样。因此，等效电路模型至少需要三个节点，有时甚至需要更多。我们将思路转回到两个电容器的物理模型，假设每个电容器的极板都由电路中的一个节点表示，可以看到，等效电路模型至少需要像下图中的电路一样复杂，有四个节点。请注意，由于沿导线也存在电荷分离，因此增加了一个与导线电感并联的小电容。

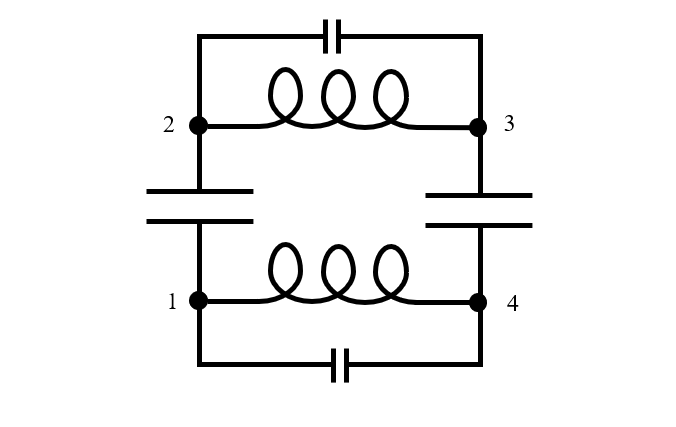
两个串联的有限大小的无损耗电容器的等效电路模型。

希望您能从这个例子中看到，在共振频率附近构建一个有效的等效电路模型会变得非常复杂，需要对物理场的深入理解、对类似设备的丰富经验以及数值模拟。

回到最初的问题，可以说电容、电感甚至电阻都不是独立存在的概念，它们只存在于彼此的组合中。虽然我们有时可以将与频率有关的设备阻抗简化为单一的电阻、电容和（或）电感，但这种简化只在设备的谐振频率以下有效。牢记这一点可以帮助您避免各种陷阱，无论是这个有趣的双电容悖论还是更难以求解的复杂现实问题。

结束语

在这篇博客中，我们使用了一个经典的思想实验来理解为什么在共振频率附近工作的电磁设备的阻抗不能被分解成单一的等效电阻、电容和电感。像双电容悖论这样的思想实验，对于拓宽我们对电磁学的认识和解释计算模型的结果非常有价值。

扩展阅读

如果你想了解如何利用建模和仿真来解决其他难题，可以查看 COMSOL 博客上的其他示例:

• 点亮一个灯泡需要多长时间？
• 电压和接地是否存在？
• 为什么三相输电线路中的损耗不平衡？
• 单根直导线中存在电感吗？