
许多机械组件都是在振动环境中运行的,如果组件的特征频率较低,就有可能引起共振。无论是对汽车内饰件的轻微干扰、高精度制造中的临界误差,还是土木工程中的危险失效,都会造成不同程度的影响。这篇博客介绍了如何利用形状和拓扑优化最大程度地提高最低特征频率,从而降低共振的可能性。COMSOL Multiphysics®软件的内置功能允许使用基于梯度的优化来解决这些问题。
机械共振简介
当机械系统受到频率与系统固有频率相匹配的力的激励时,就会产生机械共振,从而导致高振幅振动。我们可以在例如手表和乐器中利用这种效应,但本文我们将重点讨论需要避免的共振,这些共振可能会导致机械疲劳,或土木工程中的失效等问题。可以采取多种措施来减少共振,例如安装主动或被动隔振系统,或引导用户避免引起共振的行为。例如,在如下图所示的一座著名的伦敦大桥上,一个指示牌要求士兵们在过桥时换便步走,以避免行进时的统一节奏引起危险的机械共振。
避免产生机械共振的另一种简单策略是,提高最低固有频率。在此,我们将探讨如何通过优化来实现这一目标。

伦敦阿尔伯特桥上有一个指示牌,提示士兵在桥上打乱步伐行走,以避免共振。原图由 Colin Smith 提供,经CC BY-SA 2.0许可,通过Wikimedia Commons共享。
优化简介
所有优化问题都由许多设计变量组成,这些变量需要通过优化算法来改变,以提高某个特定的量,即目标函数。此外,还可能存在需要求解其他不能超过某些界限的变量,也称为约束条件。在 CAD 背景下,目标通常使用仿真计算。
对于优化算法,我们可以作如下区分:
- 无梯度优化,即只使用目标值和约束条件值来更新设计变量的优化
- 基于梯度的优化,了解目标和约束条件对设计变量变化的敏感程度的优化
基于梯度的优化在每次迭代中都能获得更多信息,因此速度明显更快,尤其对于设计变量较多的问题。由于速度差距之大,因此第一种方法对于形状和拓扑优化的大多数应用来说都是不实用的。COMSOL Multiphysics®支持此处列出的两种优化算法,但本文将重点讨论基于梯度的优化。
在下面的例子中,我们的目标是最大程度地提高最小特征频率,也可以最大化与环境中自然出现的某些不需要的频率之间的距离。特征频率问题经常出现的一个方面是,即使结构包含设计对称性,其特征模态也可能是非对称的。因此,每次迭代都必须对整个结构进行模拟。不过,如果初始设计是对称的,则可以使用COMSOL中的形状优化或拓扑优化接口中的镜像对称功能保留对称性。
形状优化
第一个示例为一个一端固定的壳模型。通过对边界变形\mathbf{d},应用基于偏微分方程的正则化来保持法向量的连续性,类似于拓扑优化中使用的亥姆霍兹滤波器,即:
式中,d_\mathrm{max}是最大位移,L_\mathrm{min}是滤波长度,d_\mathrm{max}/L_\mathrm{min}是变形的最大斜率,\mathbf{c}是边界变形的控制变量场。对实体进行形状优化时,还有一个用于平滑内部单元的偏微分方程,但在实际操作中,一切都使用形状优化接口中的自由形状域,自由形状边界和自由形状壳功能处理。这些功能只能在基于梯度的优化中使用。除了基于偏微分方程的形状正则化之外,我们还可以使用多项式正则化技术或对几何结构进行简单的更改,如平移、旋转和缩放。(有关平移和缩放的更多信息,请参阅电磁学中的形状优化系列博客。)下面的动画演示了在保持设计对称性的同时,使用基于偏微分方程正则化的结果。
在整个优化过程中,壳的设计都是变化的。
切换处理模式时,始终求解前六个特征频率,并使用移动渐近线法(MMA)最大化最小特征频率。
第二个示例是一个实心支架,但支架的几何形状有点像壳,因此需要保留支架臂的厚度。这可以结合广义拉伸算子与指定变形功能来实现(更多信息请参阅 COMSOL®案例库中的支架-特征频率形状优化教学案例)。除此之外,就目标和对称的实现而言,此模型的设置与之前的模型类似,但初始设计并没有那么糟糕,因此优化并不明显(如下图所示)。
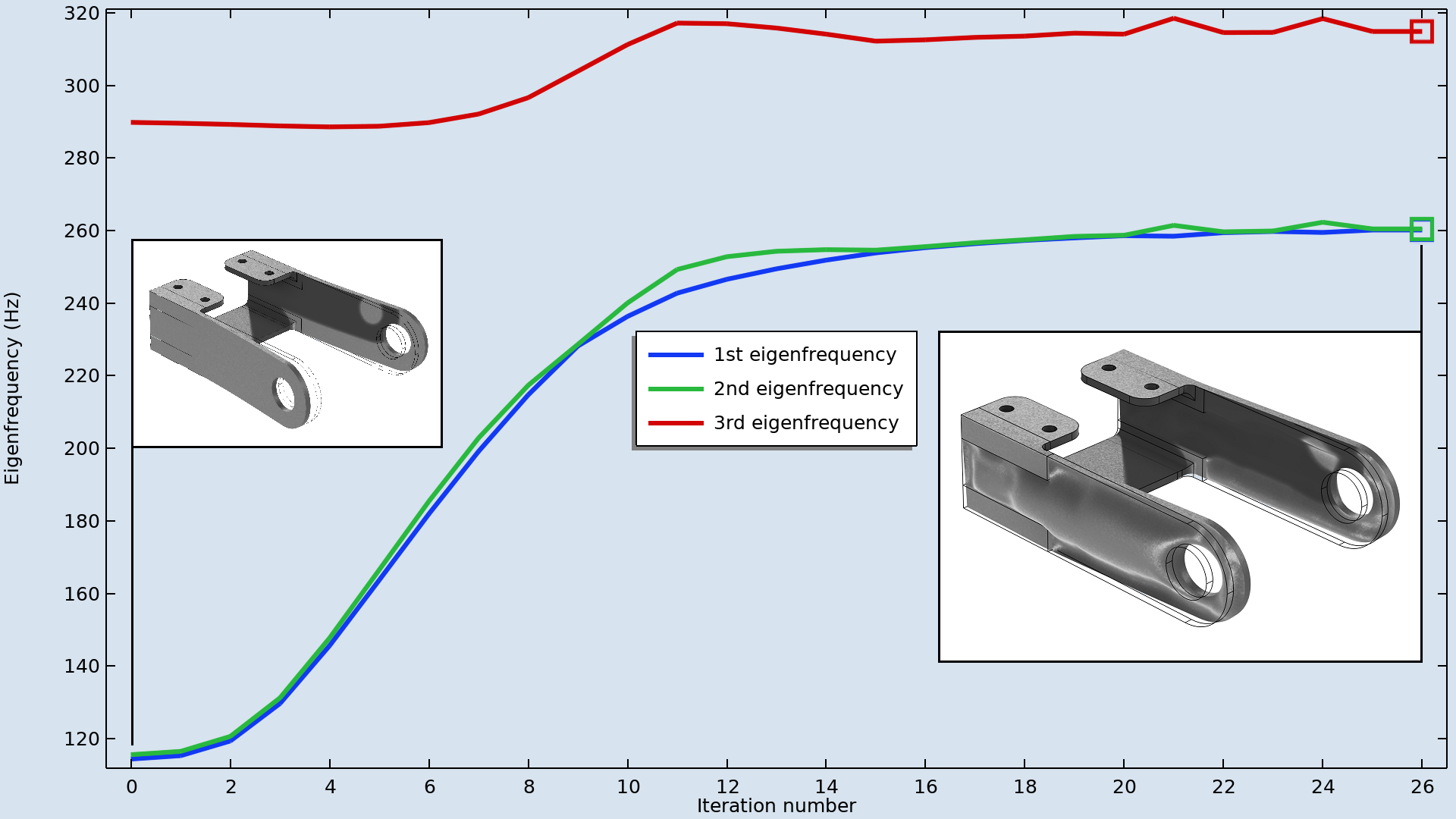
用插图表示的优化过程,分别说明了第一和第二特征模式的初始和优化支架几何结构。图中的支架被固定在四个小孔上。
拓扑优化
在进行拓扑优化时,尤其是使用软件中的拓扑优化接口时,也可以使用基于梯度的优化。关于拓扑优化的详细介绍,请参阅博客:“通过密度方法进行拓扑优化。”基本思路是引入一个随空间变化的、边界在 0 和 1 之间的设计变量场\theta_c,分别对应空域和固体材料。对于结构力学来说,密度和杨氏模量(刚度)都取决于这个变量。这种依赖关系并不明确,使用最小长度尺度L_\mathrm{min}对问题进行正则化是有利的。此外,还需要以不同于刚度E的方式对密度\rho进行插值,以防止设计变量的中间值因其良好的比刚度而在优化设计中占主导地位。设计变量场与材料特性之间的关系由以下公式给出:
式中,\theta_f是滤波设计变量,\beta是投影斜率参数,p_\mathrm{SIMP}是固体各向同性材料罚函数的参数。这些参数会对优化设计产生很大影响,因此为了避免出现不良的局部极小值,有必要对这两个参数的多个组合进行优化求解。也就是说,要对优化问题进行参数化扫描求解,如下图中的梁示例所示。这个梁一端固定在左侧,另一端支撑一个占总重量15%的重物。梁承受40%的体积约束。拓扑优化问题针对(p_\mathrm{SIMP}, \beta)的五种参数组合求解, 即 (1, 2), (2, 4), (3, 8), (4, 16), 和 (5, 32)。预计初始优化的连通性和灰度较差,但这些非物理设计为后面的优化提供了良好的初始设计。
在整个优化过程中,梁的结构都是变化的。位移通过\theta=0.5等值线上的颜色显示。
在进行拓扑优化时,最好在过滤器数据上进行仿真验证。在 COMSOL案例库的教学模型中,对此模型进行了验证,并且结果显示,与原始优化结果相比,拓扑优化后的设计在更高的特征频率下性能更好。这是意料之中的,因为隐式设计表征法会使实体–空腔界面附近的材料刚度降低。
最后,这里显示的是单一的优化结果,但通过使用不同的体积分数、附加质量或最小长度尺度值,可以轻松生成不同的设计。
结论
在 COMSOL®中,可以利用形状和拓扑优化实现特征频率的最大化。对称条件通常无法强加给物理场,但我们可以对优化进行限制,以便仍能产生对称设计。如果目标是将到某个不需要的频率的距离最大化,也可以采用处理模式切换的最大/最小策略。
要获得特征频率最大化的实践经验,请至 COMSOL®案例库下载文中提到的示例:



评论 (0)