
之前的博客文章分享了一种在三维稳态模型中通过平行切面生成动画的后处理技巧。今天,我们将讨论另一个后处理技巧:如何计算并绘制任意变量在多个平行截面上沿轴向坐标的最大值(最小值、平均值或积分)。
后处理的目标
三维模型的任意场变量u = u(x,y,z)在各个xy平面上具有不同的最大值,正如下图中zi和zi+1平面分别对应不同的最大值(umax)i和(umax)i+1。本文的目标是绘制 ith平面上沿轴向的场最大值(umax)i图。有多种方式可解决这个后处理问题。
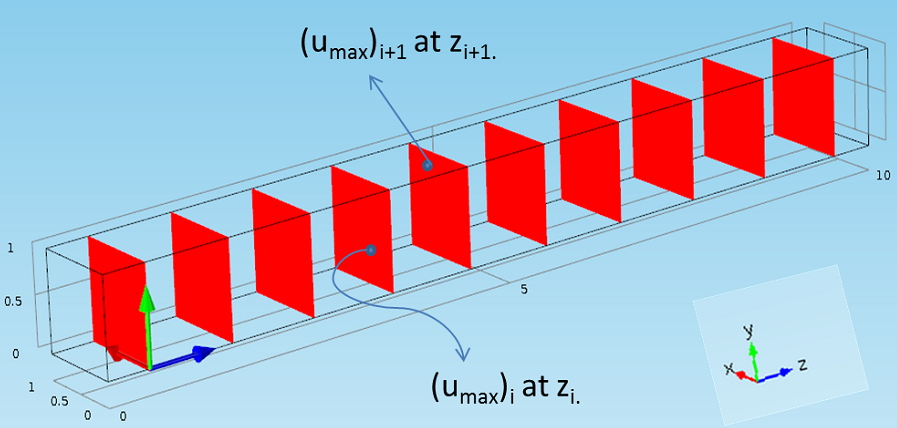
图像展示了平行截面上不同的场最大值。
截面数据集
第一种方式是使用内置的后处理特征,例如“截面”数据集和“表面最大值”特征。您可以在z轴的特定位置创建截面数据集,该平面上任意变量的最大值都可以通过“表面最大值”特征(路径为“派生值 > 最大值 > 表面最大值”)获得。借助这一方法,可计算出单个z轴位置的横截面最大值。为了获取所有横截面上的最大值,我们必须多次重复这一步骤。
LiveLink™forMATLAB®
上述的手动操作可以利用LiveLink™forMATLAB®通过简单的 ‘for’ 循环语句自动完成。内置的包裹函数 ‘mphmax’ 可对“截面”数据集启用最大值计算。鉴于模型中已定义了“截面”数据集,于是可以方便地通过下方代码计算z = [z1, z2, …, zn]时的最大横截面值(矢量umax具有 ‘n’ 个值)。
z = [z1 z2 z3 zn]; for i = 1:length(z) model.result.dataset('cpl1').set('quickz', z(i)); umax(i) = mphmax(model,'u',2,'dataset','cpl1'); end plot(z, umax)
参数化扫描和辅助扫描特征
我们可利用“参数化扫描”或“辅助扫描”特征为任意指定参数(用于定义几何、网格和物理场设置)的多个值运行 COMSOL Multiphysics 仿真。因为这些扫描特征本质上等同一个 ‘for’ 循环语句,所有我们便能利用这两个特征来进行后处理分析。
让我们看一看在静态层流混合器模型中,为速度场幅值创建横截面最大值绘图涉及了哪些步骤。下方的切面图显示了z轴不同位置的速度场幅值。我们的目标是获取每个切面(横截面)的最大速度场幅值,并为这些切面最大值绘制出随z坐标的变化趋势。
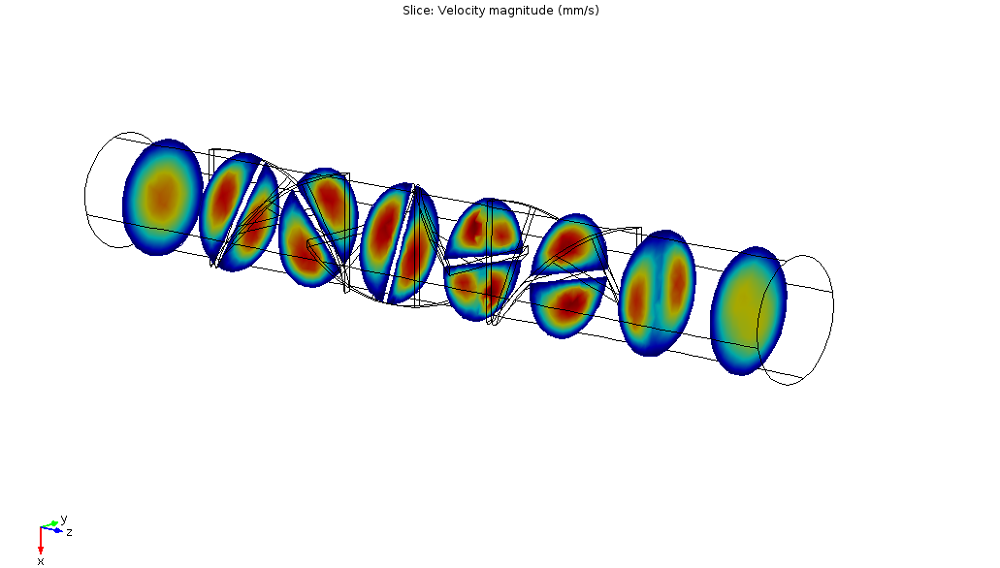
“静态层流混合器”模型的速度场切面图。
步骤 1
第一步,添加轴向坐标的对应参数。对于这个示例模型,我们添加了参数zp,如下方截图所示。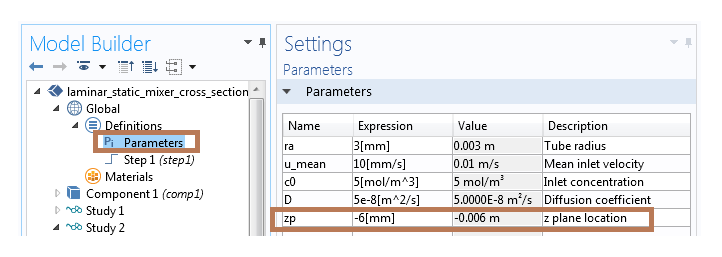
向“参数”表中添加参数。
步骤 2
接下来,我们需要添加第二个研究(具有稳态步骤)以运行关于参数zp的“辅助扫描”或“参数化扫描”。添加第二个研究步骤的唯一目的是重构可用的解数据,为达成后处理目标做准备。因此在这一步中,不求解任何物理场接口,只需将“研究 1”的解传送到这个新建的研究中。
设置好上述“稳态”步骤(如下方截图所示)后,我们需要对第二个研究步骤进行计算。
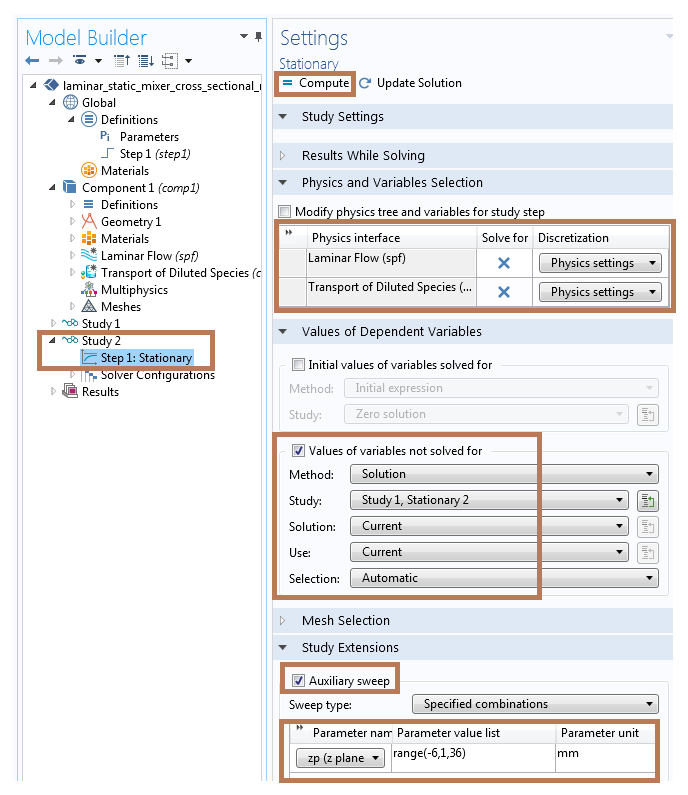
“稳态”步骤设置,可在不求解物理场接口的情况下,运行“辅助扫描”特征。
步骤 3
现在让我们来添加“参数化表面”数据集(右键单击“结果”节点下的数据集,从“更多数据集”子菜单中选择“参数化表面”)。在“参数化表面”的设置窗口中选择“Study 2/Solution 1”作为数据集,并使用参数zp作为z坐标表达式。设置如下图所示。
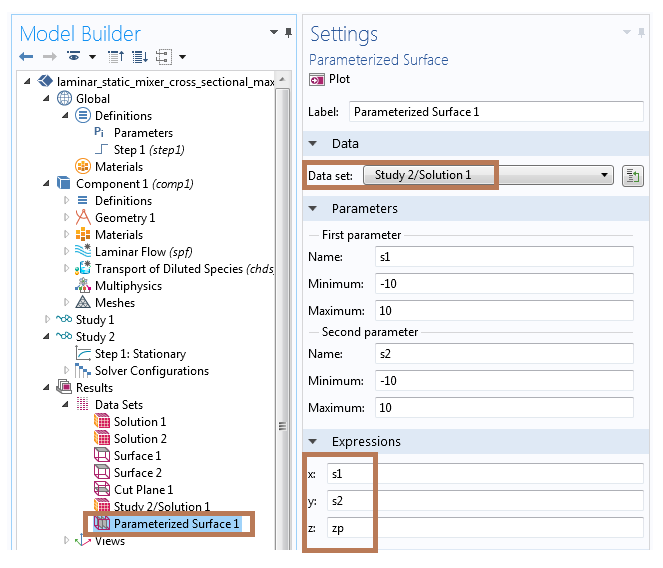
用于创建“参数化表面”数据集的设置。
步骤 4
接下来,向模型添加“表面最大值”节点(右键单击“结果”节点下的派生值,从“最大值”子菜单中选择“表面最大值”)。我们利用“参数化表面”作为数据集来计算“表面最大值”,如下方的截图所示。完成设置后,单击计算以创建表格,对每个z坐标值对应的表面最大值(速度幅值)进行汇总。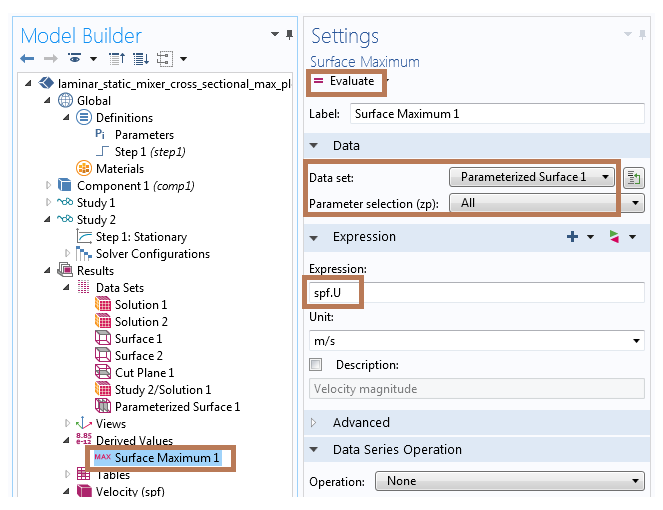
使用“参数化表面”数据集计算“表面最大值”的设置。
步骤 5
最后,单击表图按钮(如下图所示)开始绘制表格数据。一维绘图显示了最大速度场幅值与z坐标位置之间的关系。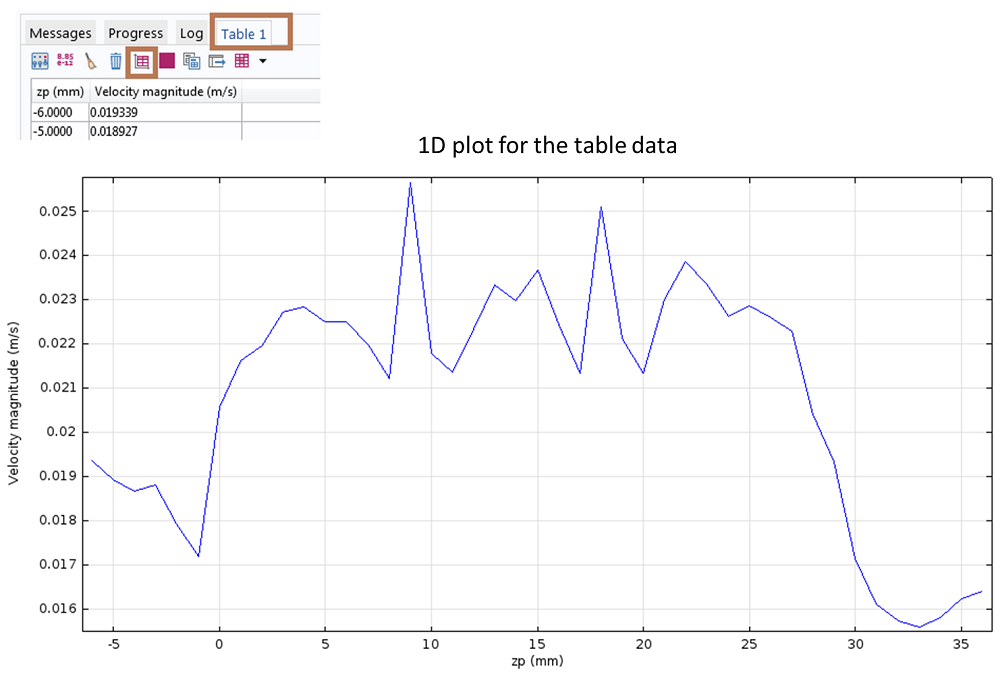
一维绘图显示速度场幅值在不同 z 坐标位置上的横截面最大值。
总结
本文介绍了一个简单又强大的后处理技巧,可用于自动计算平行面上任意变量的最大值(最小值、平均值或积分)。本文内容的重点是如何使用 COMSOL Multiphysics 的内置扫描功能重构解数据,使其符合后处理目标。我们还展示了一段使用 LiveLink™forMATLAB® 的脚本方案,仅需几行代码便能完成这一后处理任务。
敬请关注本系列的下一篇博客文章,了解更多提示和技巧!
MATLAB 为迈斯沃克(MathWorks)软件公司的注册商标。所有其他商标均属其各自所有者所有。有关此类商标所有者的完整信息,请参见http://www.comsol.com/tm。COMSOL AB 及其子公司和产品并不从属于这些商标的所有者、或受其认可、或接受其赞助、或获得其支持。



评论 (0)