
作为有史以来最伟大的两位数学家,莱昂哈德·欧拉(Leonhard Euler)和约瑟夫·路易斯·拉格朗日(Joseph-Louis Lagrange)对连续介质力学做出了许多贡献。他们对变形物体建模的各自研究的结合,启发了任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)方法 ,一种广泛用在很多仿真应用中的技术。通过阅读这篇博客,您可以了解欧拉和拉格朗日如何创建ALE方法,以及如何使用此方法在 COMSOL Multiphysics 软件中进行建模。
欧拉和拉格朗日
莱昂哈德·欧拉 1707 年出生在瑞士巴塞尔,他是一位多产的数学家,一生共发表了800多篇文章。他师从著名学者约翰·伯努利,并在巴塞尔大学获得哲学硕士学位。在搬到俄罗斯圣彼得堡大学工作之前,欧拉向巴黎科学院有奖征文大赛提交了他的第一篇论文,年仅 19 岁的他获得了二等奖。

莱昂哈德·欧拉的肖像。图像通过Wikimedia Commons 在公共领域获得授权。
欧拉很快在学术界得到晋升,并于 1733 年接替伯努利在圣彼得堡大学担任数学教授。 1741 年,在腓特烈二世(Frederick II)的邀请下,欧拉搬到了柏林。在那里的25年间,他写了大约 380 篇文章和创新性著作Introductio in Analysin Infinitorum的第一卷,这本书首次正式定义了函数;介绍了符号f \left( x \right);普及了符号e和\pi;建立了临界方程e^{i\theta}= \cos \left( \theta \right) + i \sin \left( \theta \right)。
拉格朗日出生在意大利都灵。今天,这座城市是意大利皮埃蒙特地区的首都。1736年拉格朗日出生的时候,这座城市作为撒丁王国(Kingdom of Sardinia)领土的一部分,由萨瓦公爵(Duke of Savoy)统治。拉格朗日对数学表现出了浓厚的兴趣,开始独立研究新的课题,与与欧拉有书信往来,并于后者离开柏林后,接任了其职位。

约瑟夫·路易斯·拉格朗日的肖像。图像通过Wikimedia Commons 在公共领域获得授权。
在柏林,拉格朗日完成了他著名的的大部分数学理论。他在变分法的发展中发挥了重要作用,并提出了拉格朗日力学方法。尽管拉格朗日力学做出了与牛顿运动定律相同的预测,但是对于许多问题的经典力学问题,他引入的拉格朗日函数可以在数学上比牛顿力学以更直接、更有洞察力的方式进行描述。他还发展了拉格朗日乘子法,可以在变分方法中很容易地引入对方程组的约束。
欧拉方法和拉格朗日方法比较
欧拉和拉格朗日的数学公式是有限元法求解 COMSOL Multiphysics 方程的基础。
在欧拉方法中,系统的动力学是以一个观察者在一个固定坐标系下测量系统演化的角度来考虑的。这个坐标系在 COMSOL Multiphysics 中被称为空间坐标系,我们可以这样理解:它对应于物理分析中的实验室坐标系,这是一个根据一组固定的轴定向,而不涉及物理系统自身各组成部分的坐标系。
下图显示了一个建立在二维(2D)平面中的薄板材料的结构力学模型。该板固定在左侧的刚性墙上,由于重力向下作用,板在自身重量的作用下会变形。正如在实验室中所期望观察到的那样,由绘制在空间坐标系中的结果我们可以观察到物体的变形。

在空间(实验室)坐标系中观察时,固定在左侧灰色块上的薄板会在自身重量的作用下变形。在给定的机械性能下,尖端的挠度约为 5 毫米。
用欧拉方法表述物理方程似乎很自然。事实上,这是电磁学和流体物理学等问题的通用格式,其中场变量表示为空间坐标系中固定坐标的函数。
然而,对于力学问题,拉格朗日方法提供了另一种有用的思路。在拉格朗日方法中,力学方程是根据无限小的个体材料编写,当物体动态位移或变形时,材料会在物体内移动。换句话说,从拉格朗日坐标系的角度来看,物体本身总是不变形的,因为坐标系始终保持附着在变形物体上并随其移动,但是从变形物体的角度来看,似乎是周围的外力改变了方向。与变形物体一起移动的相应坐标系在 COMSOL Multiphysics 中称为材料坐标系。
在空间坐标系中测量的物体内的某一点,该点的机械位移使其与材料坐标系中同一点的位置发生偏移。在下图中,我们将视角聚焦在上例中变形板的顶端并将通过动画来表示变形,随着物体密度的增加,其重量也会增加。正如我们所看到的,随着物体在空间坐标系中的尺寸变化,材料坐标系 (红色网格和箭头)也随之一起变形。这代表如复合材料的机械性能等各向异性材料性能,可以在材料坐标系中方便地表达。
随着密度的增加,薄板顶端在自身重力作用下发生变形的放大图。红色网格表示在空间(实验室)坐标系中看到的与物体相关联的材料坐标系中的坐标。红色和绿色箭头表示在空间坐标系中可以查看的材料坐标系x和y坐标方向。
对于这类力学问题,在非常小的应变限制下,空间和材料坐标系几乎重合,因为与物体的尺寸相比,机械位移很小。在这种情况下,通常使用“工程应变”来定义物体的弹性应力-应变关系,并且所得的应力-应变方程是线性的。然而,随着机械位移的增加,用于评估工程应变的线性近似越来越不准确——因此需要精确的格林-拉格朗日应变。在 COMSOL Multiphysics 中,“几何非线性”一词意味着使用了格林-拉格朗日应变。
有关数学的更多详细信息,请参考我的同事Henrik Sönnerlind撰写的关于几何非线性的博客文章。
在 COMSOL Multiphysics 中,根据计算的机械位移引起的坐标系变化,允许通过空间坐标系与材料坐标系分开处理几何非线性。使用材料坐标系来表达例如各向异性机械材料等属性仍然很方便,因为即使物体变形,这些属性通常也会与材料坐标系坐标保持一致。
相比之下,重力等外力在空间坐标系中具有固定的方向。从材料坐标系的角度来看,重力等外力随着物体变形而改变方向。下图显示了上述薄板的尖端,但是在这里,位移大小是用颜色绘制的。箭头用于说明由于重力引起的力,用材料坐标系坐标表示。由于材料坐标系坐标相对于物体保持固定,因此物体的尺寸不会改变。然而,位移大小会随着物体重量的增加而增加,并且在更大变形的情况下,重力相对于变形的材料逐渐改变方向。
薄板顶端受自重力的作用变形随密度增长而变化的放大图,位于拉格朗日公式使用的材料坐标系中,因此尽管位移增加,变形不明显。红色箭头指示从变形物体内的参考材料坐标系感知到的视在重力方向(在空间坐标系中是恒定的)。
拉格朗日公式和欧拉公式都不比彼此更“物理”或“正确”,它们只是描述相同现象和方程的不同数学方法。通过坐标变换,我们总能把任何现象的物理方程从材料坐标系变换到空间坐标系,反之亦然。然而,从解释和实现的角度来看,每种方法都有一定的优势和常见的应用。下表总结了其中的一些内容:
| 优点 | 常见应用 | |
|---|---|---|
| 欧拉方法 |
|
|
| 拉格朗日方法 |
|
|
什么是 ALE 方法?
那么对于多物理场问题,例如流-固耦合(FSI)或几何非线性机电学又是如何计算的呢?对于这些情况,一个物理方程可以用欧拉方法最自然地表述,而另一个可以用拉格朗日方法更好地表达,这就是 ALE 方法的来源。这种方法在第三个坐标系上求解方程,不需要匹配空间坐标系或者材料坐标系坐标。
第三个坐标系在 COMSOL Multiphysics 中叫做网格坐标系。在空间坐标系和底层网格坐标系之间有一个数学映射,在材料坐标系和底层网格坐标系之间也有一个数学映射。因此在所有时间点,在空间和材料坐标系中制定的方程可以被转换成要求解的网格坐标系。
在模型中代表实体的区域中,使用拉格朗日公式中的结构力学方程来预测机械位移,其中的空间和材料坐标系的关系由机械位移给出,如上所述。ALE方法添加了更多的方程,以允许相邻域中网格单元的视在位置和形状在空间坐标系中位移,这是为了说明机械变形是如何改变欧拉公式中描述物理的任意区域的边界形状的。这些附加方程在 COMSOL Multiphysics 中被称为移动网格或者变形几何。
在拉格朗日域和欧拉域之间的边界处,这些附加方程的边界条件要求欧拉域中空间坐标系的位移(通过移动网格定义)必须与拉格朗日域中材料坐标系相应的空间坐标系的机械位移相匹配。即使在没有求解力学方程的情况下,例如没有使用拉格朗日方法,ALE方法仍然可以用来表示由于材料沉积或损失而产生的移动边界。
ALE方法在多物理场建模中的应用
如果你觉得 ALE 方法太过于数学化,确实它是一个抽象的难以理解的概念。那么,为了更好地理解 ALE 方法的工作方式,我们来看一个在 COMSOL Multiphysics 中建模的例子。
微泵机理中的流-固耦合
ALE 方法在流-固耦合建模中起着重要作用。在 COMSOL Multiphysics 中,这种方法实现了流体流动和结构变形的自动双向耦合,COMSOL案例库中的微泵机理教程模型演示了这种技术的使用。
微泵机理的核心是两个悬臂,其功能与传统泵装置中的阀门相同。这些悬臂足够灵活,流体流动使它们发生变形。当流体在顶部交替地被泵入或泵出通道时,流体流动的力导致两个悬臂变形,使流体从右侧流出或从左侧流入。
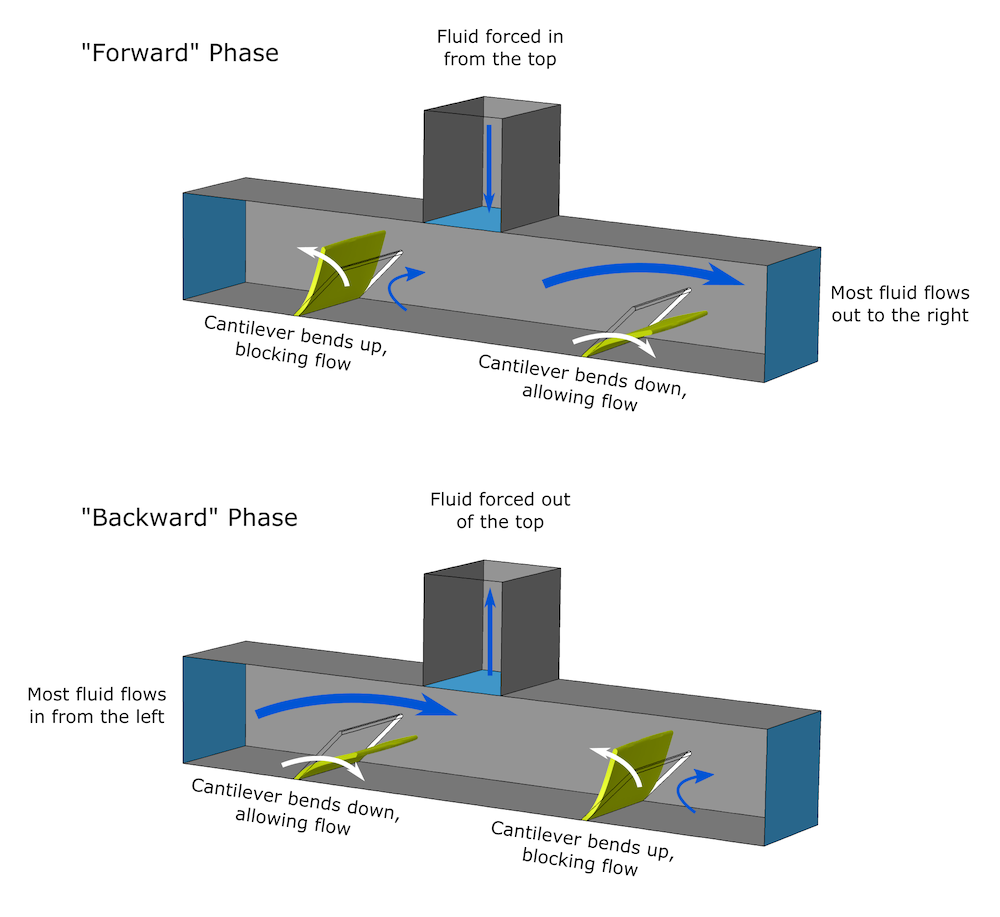
微泵机理。将流体泵入或泵出顶部管道会在两个悬臂中产生相反的反应,将流体推入或推出腔室。尽管没有时均净流量进入上部管道,但存在从左到右的时均净流动。
悬臂变形足够大,以至于流体和固体交汇处的边界位置有明显的变化:这是一种几何非线性情况。流–结固耦合接口自动处理流体对固体的压力和固体对流体的力,以及网格的变形,其中采用ALE方法来计算固体和流体区域的形状变化。
对于实体,具有几何非线性的力学方程定义了空间坐标系相对于材料坐标系的位移。在流体方程中,有必要对求解方程的网格进行变形,以便在定义流体方程的空间坐标系中表达固体边界的位移。边界处的变形由计算得到结构问题的机械位移控制。然而,在流体中,网格节点的确切位置或方向并不重要,因为方程是在固定的空间坐标系中表达的。相反,需要对网格变形进行平滑处理,以确保数值问题在高质量的网格单元下保持稳定。
为了解释 FSI 问题的 ALE 方法,我们可以用广义相对论的一个常见解释来解释:由于流体流动产生的力(欧拉)告诉结构如何在材料坐标系中变形(拉格朗日),而结构变形(拉格朗日)告诉网格如何在空间坐标系中移动(欧拉)。
顶部:微泵工作过程,包括压力、流量和悬臂变形,如空间坐标系中所示。底部:通过ALE方法计算的网格变形。
从 COMSOL Multiphysics 5.3a 版本开始,用于定义对这类问题中网格变形的移动网格特征位于组件>定义节点下。即使模型中包括多个物理场接口,这也可以使模型中所有物理场之间的材料和空间坐标系的定义保持一致。下面的屏幕截图显示了这些设置在 COMSOL Multiphysics “模型开发器”树中的位置。
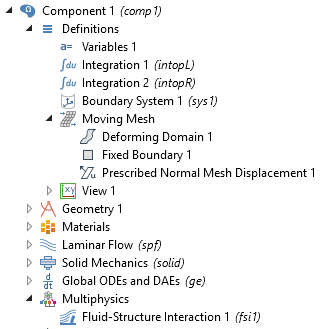
屏幕截图显示了组件 > 定义节点下的移动网格特征,以及通过多物理场 > 流固耦合在两个物理接口之间进行耦合。
铜沟槽中的电沉积
沟槽中的铜沉积教程模型中的铜沉积表明,ALE方法对于模拟电沉积问题至关重要。在这个模型中,铜沉积在具有小沟槽的电路板上。与沟槽的整体尺寸相比,沉积的铜层变厚,因此,随着沉积的进行,铜表面的尺寸和方向会发生明显变化。由于在该表面上的不同点处的铜沉积速率不均匀,因此不能忽略边界的形状和移动。
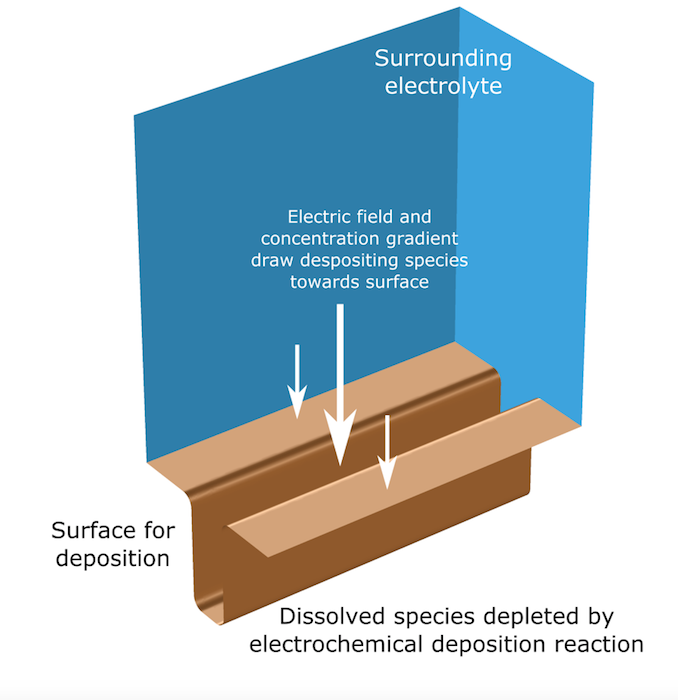
电沉积模型中正在求解的物理问题的示意图。
为了计算铜电极-电解质界面上给定点的沉积速率,我们需要该点附近溶液的物种浓度和电解质电势。随着沉积的进行和边界的移动,电解质体积的形状必须连续变化。同样,必须重新计算改变形状上的浓度和电势分布。
沉积速率与边界运动速率的耦合和形状变化的计算是用ALE方法完成的,而全自动多物理场耦合是用三次电流分布和变形几何接口完成的。这里变形几何根据电化学接口计算,以与电沉积的局部电流密度成比例的速率移动空间坐标系中的铜表面。
有了这个模型,我们可以准确地说明沉积过程,以优化其参数。我们还可以用不同的外加电位和沉积表面几何形状进行实验,以提高沉积的均匀性,从而产生更高效的工艺和更高质量的最终产品。
显示沉积过程随时间演变的动画。很明显,沉积发生不均匀,导致沟槽开口在其顶部收缩。
热消融
在之前的博客文章里,我们讨论了热消融,其中涉及对物体施加非常高的温度,导致表面熔化和蒸发。热消融的例子包括通过激光去除材料——例如在蚀刻过程、激光钻孔或激光眼科手术中,以及航天器重返大气层时的隔热罩。
显示材料热消融效果的动画。
我们预测出当物体的一些材料被移除时,物体的形状会发生变化,因此变形网格显然是热消融模拟的一个关键部分。我们需要知道的是物体的形状会如何变化,这取决于我们如何平衡施加的热量与消融的和整个结构耗散得热量损失。
为了获得这些信息,我们可以通过传热接口求解传热方程来预测作为空间和时间函数的温度分布。因为物体的质量和形状在变化,传热接口被耦合到变形几何接口,使用ALE方法根据消融率移动边界。传热方程随着物体形状的变化预测物体的温度分布。
通过执行这些步骤,我们可以获得热消融过程的精确计算。此外,我们可以确定消融完成后物体的最终形状,这可能使我们能够检查激光焊接是否在可接受的公差范围内,或者航天器是否能在紧急着陆过程中幸存。
在仿真中使用变形网格
欧拉和拉格朗日在数学领域的贡献为模拟涉及多物理场应用的各种系统奠定了基础。结合它们各自的方法导致ALE方法的发展,可以用来预测物体变形或位移时的物理行为。通过适当考虑这些运动,您可以建立高度精确的模型。当您在研究这些和其他利用ALE方法的模型时,请记得感谢欧拉和拉格朗日!
ALE 方法是 COMSOL Multiphysics 软件中许多内置物理功能之一。点击下方按钮,查看更多:
扩展阅读
- 访问这篇博客中提到的教程模型:
- 了解如何使用 ALE 方法对线性和旋转位移以及任意平移运动进行建模:



评论 (0)