多相催化建模方法

多相催化建模在化学工程界引起了极大的兴趣，因为许多工业过程都使用了这类催化作用。在这篇博客中，我们讨论了从详细的微观几何结构开始，然后通过均质化近似进行建模的步骤。遵循这些步骤，从微观粒子层面到宏观反应器层面，我们都可以详细设计催化剂，并研究这种设计对整个反应器性能的影响。

多相催化作用简介

由于基于多相催化的工业过程可以大量生产大宗化学品和精细化学品，并能大规模清除对环境有害的化学品，科学和工程界对这一过程非常感兴趣。通过数值建模和仿真来理解这一过程也成为关注的焦点。

多相催化涉及两个不同相间的界面催化反应。在这里，我们只讨论固体-流体界面的多相催化，这是工业过程中最常见的多相催化形式。在这些过程中，反应物和产物存在于与固体催化表面接触的流体混合物中，并在流-固界面发生催化反应。

常见的基于固体-流体多相催化的大规模工业过程包括通过 Haber-Bosch 法生产氨、Ostwald 法生产硝酸、Wacker 法生产环氧乙烷、通过蒸汽重整生产氢气，以及通过 Wacker 聚合生产聚乙烯和聚丙烯。

电催化剂表面的电化学反应也是基于多相催化的过程。例如氯碱、氯酸盐和水分解过程就是基于电催化的大型工业过程示例。

汽车工业中使用的催化转化器中将氮氧化物还原为氮气和氧气的步骤，是另一个广泛使用的基于多项催化的工业过程。从环境的角度来看，其他重要的过程有石油的脱硫和二氧化硫的催化氧化，这两个过程的最终目标都是减少石油产品燃烧过程中排放到环境中的硫氧化物。

能够检测微量吸附分子的传感器通常也是基于多相催化过程工作的。例如，氢气和氧气传感器就是通过电催化工作的，基于酶促反应的生物传感器也是一个示例。

主要步骤

多相催化中催化剂的作用方式与均相催化中的催化剂相同，都是降低催化反应的活化能。

我们不讨论催化剂如何实现这一目标，但我们可以简要提及大多数过程涉及的两种固体催化剂类型：酸和金属催化剂（G. F. Froment，K. B. Bischoff，J. De Wilde，Chemical Reactor Analysis and Design）。酸催化剂，如铝硅酸盐可以作为 Lewis 酸或 Brønsted 酸，并以这种方式形成活化能较低的表面络合物。金属催化剂主要包括吸附氢表面络合物的加氢和脱氢反应。

非均相反应催化反应中化学物质的主要步骤如下（Chemical Reactor Analysis and Design，H. S. Fogler’s，Elements of Chemical Reaction Engineering）：

1. 将反应物从混合物的主体输送到催化剂颗粒
2. 将催化剂颗粒孔隙中的反应物输送到活性位点
3. 反应物对活性位点的吸附
4. 反应物反应，形成吸附产物
5. 产品从活性位点的解吸
6. 催化颗粒孔隙中的产物从颗粒中移出
7. 产品从颗粒输送到大部分混合物

下面的示意图显示了催化剂颗粒横截面中的上述 7 个步骤。催化剂颗粒由催化剂载体颗粒组成。活性位点的颜色用杏色表示，位于催化剂载体的表面（蓝色图案）。

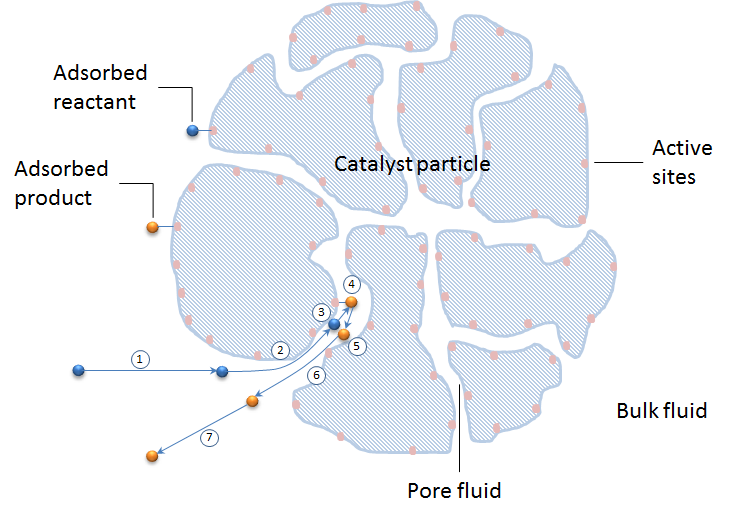
接下来，我们来看看这 7 个步骤的建模方法。我们还可以研究如何将这 7 个步骤包含在整个催化反应器的模型中，包括大量反应混合物中的物质守恒。

吸附-解吸模型

吸附主要有两种类型：物理吸附和化学吸附。

物理吸附通过范德华力发生，而化学吸附涉及化学共价键。在多相催化中，化学吸附通常是催化反应的一个必要部分。因此，这里我们只讨论化学吸附。

多相催化中最常见的化学吸附是通过Langmuir等温线进行描述。Langmuir等温线理论基于以下假设：

1. 对于不同的吸附位点和不同的表面覆盖率，吸附在能量上是均匀的
2. 假设吸附的物质形成单层
3. 吸附的分子之间没有相互作用

这里的表面覆盖率是指吸附位点被占用的比例。

Freundlich等温线是基于这样的假设：吸附是不均匀的，一些位点具有较高的吸附系数，因此首先被分子覆盖。这些位点有更多的吸附放热。吸附热与表面覆盖率呈对数关系。Temkin等温线可以通过假设吸附热与表面覆盖率的线性关系来获得。其他吸附模型（如BET等温线）也包括多层分子，这些分子必须在其描述中包括物理吸附。

表面反应

根据化学反应工程原理，在多相催化的建模中经常使用三种可能的反应机制：

单位点反应机制描述了分子的吸附及其在该位点上的异构化或分解。下图显示了一个分子异构化的示例。

双位点反应机制描述了一个反应物分子的吸附，然后与可吸附产物的另一自由位点相互作用。双位点反应机制也可以描述两种反应物先在不同位点的吸附，被吸附的物质反应形成产物，如下图所示。

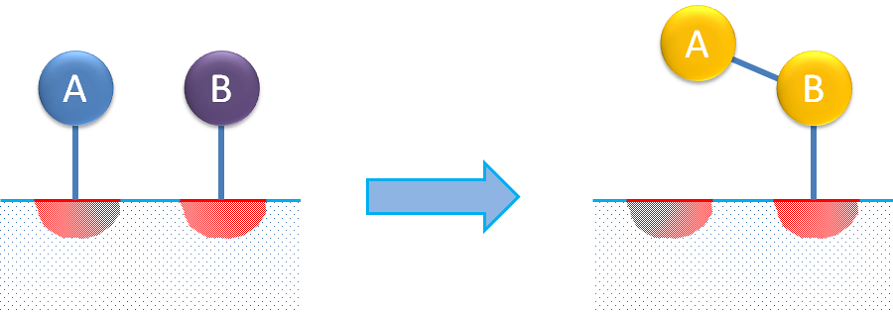
双位点和单位点反应通常被认为遵循Langmuir-Hinshelwood或Hougen-Watson动力学。

第三种表面反应机制描述了反应物分子在单个位点的吸附，其中被吸附物质与流体（未吸附）中的分子反应形成吸附产物。这通常被称为Eley-Rideal机制。

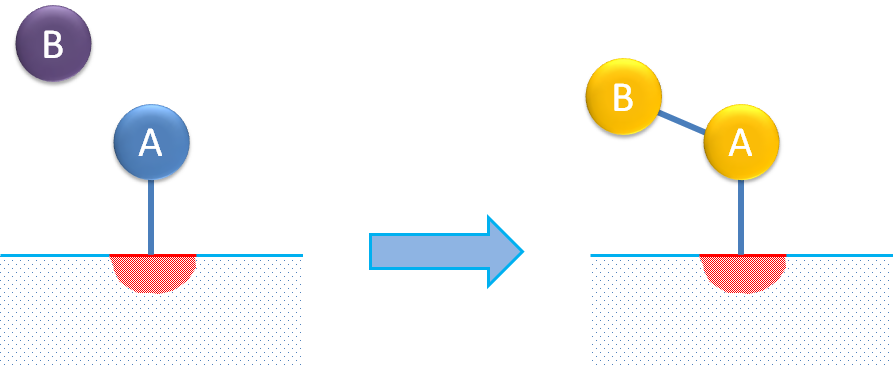
即使是最简单的单位点反应机制，当用解析为单个表达式描述时，总体速率表达式可能相对复杂。根据下面的总反应，我们可以查看一个异构化的例子：

(1)

反应机制可以表示如下：

(2)

式中，S表示活性位点、AS(ads)表示吸附反应物、BS(ads)表示吸附的产物、B表示产物。

对于这种简单的机制，即使使用质量反应定律和接近稳态的反应 1 和反应 3 的简化形式，反应速率表达式也是相当复杂的（G. F. Froment，K. B. Bischoff，J. De WildeChemical Reactor Analysis and Design）：

(3)

在方程中，\theta表示未占据活性位点的表面浓度，{c_A}和{c_B}分别表示异构体A和B的浓度。{K},{k_1},{k_2}和{k_3}是常量。

使用数值方法时，我们不需要导出机制的总速率表达式。在这种情况下，我们只需输入该机制的化学方程式即可。相反，我们必须对每个步骤的反应速率常数进行估计，同时在过程开始时对表面浓度进行估计。

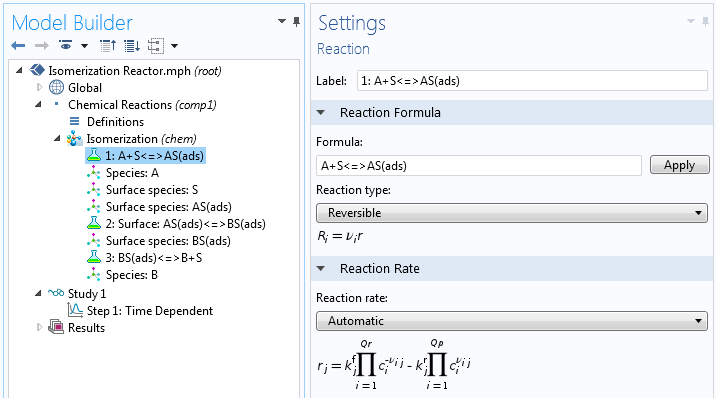
将导出解析表达式和输入完整的反应机理相结合，不做任何简化，也是一个很好的选择。原因是解析表达式包含速率常数和中间产物的浓度，这些产物可以通过测量反应的总反应速率获得。我们可以使用这些产物来估计详细机理中所有步骤的反应速率。此外，通过这种组合方法，我们还能够研究简化假设在哪些条件下有效，以及什么时候必须在模型中设置完整的反应。

输运步骤

对本体和多孔催化剂中传输的描述可以在微观尺度的颗粒水平完成，其中催化剂颗粒和孔的几何结构可以被详细描述。此外，当催化剂非常活跃时，不需要多孔结构，也可以详细描述其几何形状。

然而，当孔隙与催化剂几何结构的典型代表性基本单元的尺寸相比非常小，或者该基本单元中的孔数量太多时，对多孔催化剂进行详细的几何描述是不可行的。在这个阶段，我们可以对多孔催化剂结构使用均质化描述。

假设我们用均质模型处理催化剂的微观结构。当我们研究整个反应器中本体混合物中的传输时，仍然可以使用详细的模型来描述由颗粒组成的结构。

当颗粒数量太多并且颗粒床的几何结构过于复杂时，也必须使用本体混合物规模的均质化。

让我们来看看这 4 种可能的建模方法：

1. 催化剂微观结构的详细描述
2. 对每个颗粒的均质化描述
3. 详细描述大多数颗粒的结构，其中单个颗粒的描述是均质的
4. 颗粒床的均质化与颗粒的均质化描述相结合

微观尺度

随着X 射线显微断层扫描技术的发展，以及从事建模和仿真工作的工程师和科学家使用的计算机性能的提高，对非常复杂的不规则结构进行建模的可能性也已经增加。

电池中多孔催化剂的一小部分。

此外，制造具有明确定义的催化剂和孔几何机构的微观结构的能力，也增加了使用其详细几何结构研究这些规则结构的兴趣。根据上图，让我们来看一个假设由规则的几何通道构成的催化剂颗粒的示例。该几何结构由大约一百个重叠的催化剂颗粒组成，它们共同形成了一个直径约为 10 微米的球形催化剂颗粒。催化剂颗粒之间的空隙形成一个曲折的微通道系统。

使用材料守恒方程描述建模域中的累积和通量守恒。将吸附、反应和解吸过程描述为催化剂颗粒表面的边界条件。颗粒本身不是建模域的一部分;只有颗粒外部的流体和颗粒内部孔隙中的流体是建模域的一部分。在没有均相反应的情况下，物质_i在流体中的物质守恒方程为：

(4)

式中，\bf{N_i}表示物质的通量矢量_i。

对于催化反应中物质_i的消耗或生产，代表催化剂表面边界处的物质通量由反应速率R_i给出：

(5)

其中，{\bf{n}}表示催化剂表面法向向外的矢量。

下图显示了颗粒周围流动和反应物浓度的模拟结果。表面图显示了在催化剂颗粒表面发生反应的物质的浓度。流线显示了速度场。

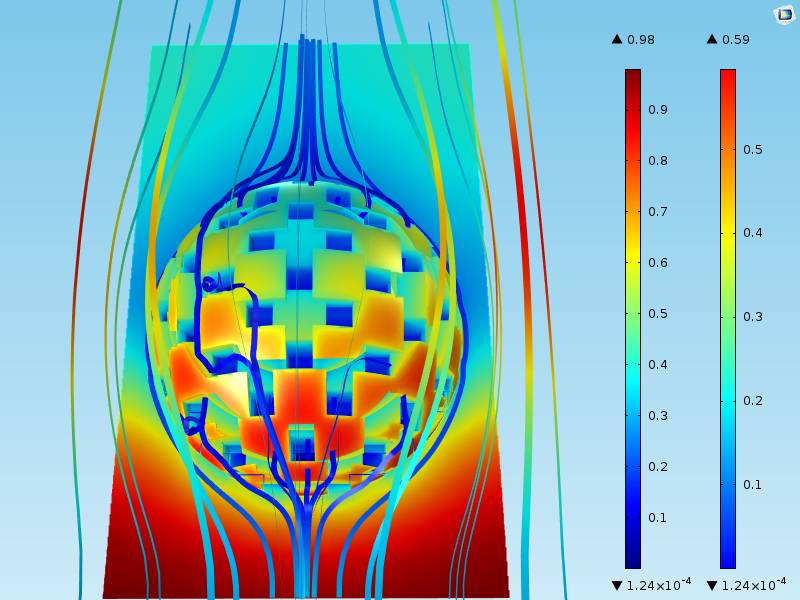
我们可以看到，颗粒周围体积的浓度在入口处（在结构域底部）的 0.98mol/m³和出口处（在域的顶部）的 0.4mol/m³之间变化。此外，在球体底部的催化剂颗粒表面的最高浓度为 0.59mol/m³。这意味着即使流体首先与球体下部的催化剂颗粒接触，也存在质量传递边界层，其浓度变化约为 0.30mol/m³（= 0.98-0.59）。

球体和球体表面之间的浓度差在球形催化剂颗粒周围变化。这个质量传递边界层对应于上文“主要步骤”部分概述中列出的步骤 1。

并不是所有反应物分子都在催化剂颗粒的外表面被消耗掉。一些分子扩散到多孔结构中，随后在孔壁表面，即多孔颗粒内的催化剂颗粒表面吸附和反应。这个传递过程对应于列表中的步骤 2。

微观尺度上的均质化

如果想对大量粒子进行建模，那我们就不能像上面显示的那样对几何结构进行详细建模。在这种情况下，我们可以通过均质化对多孔结构进行建模。从本质上讲，这意味着将多孔颗粒视为一个包含流体和催化剂的均匀板。流体是利用描述中的孔隙率进行建模的，其有效传输特性取决于颗粒的孔隙率和迂回度。

均质化后，吸附、反应和解吸过程成为物质平衡中的源和汇。换句话说，它们不再被描述为流体域的边界条件。相反，反应被表示为催化剂颗粒多孔域中的源或汇。

(6)

在这个方程中，{S_a}表示颗粒的特定催化表面积，即每单位体积的表面积。

此外，我们现在有两个不同的建模域和两组不同的域方程：一个用于颗粒周围的本体流体，没有催化反应项，另一个用于多孔颗粒。在这两个域之间的内部边界，化学物质的浓度和通量具有连续性。

我们还在流体流动方程中发现了连续性，对于大量流体，由纳维-斯托克斯方程描述，而 Brinkman 方程可以描述多孔域中的流体流动。

下图显示了均质颗粒表面和周围的流场和浓度。请注意，表面现在仅显示多孔颗粒外表面的浓度。在上面的详细案例中，表面图描绘了颗粒的表面一直到颗粒的中心。

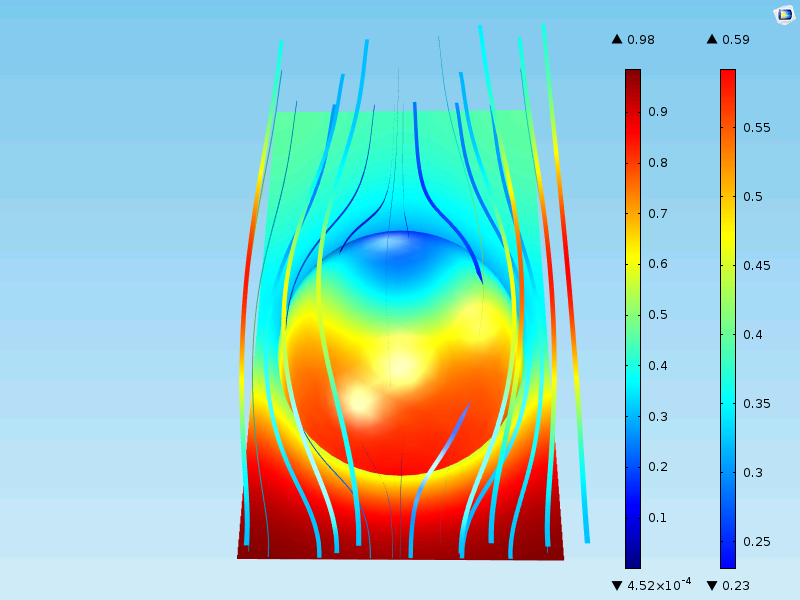
上图的仿真结果接近包括完整几何描述的结果。颗粒表面的最大浓度为 0.59mol/m³，颗粒中间最小值几乎为 0mol/m³，与详细描述的情况一致。此外，基本单元的出口约为 0.40mol/m³，与详细说明的情况也一致。

为什么会有很好的一致性呢？这是因为与颗粒的总尺寸相比，详细几何结构中的催化剂颗粒相对较小。当催化剂颗粒变大且形状更不规则时，均质化就不那么准确了。

在均质化和详细描述的情况下查看颗粒内部浓度也可能很有趣。下图显示，颗粒中的浓度分布在均质化模型中也得到了很好的描述。如果我们想将其用于设计，均质化模型对颗粒内部的传递和反应能够很好地描述是非常重要的。反应分布图显示了催化剂内部构成在吸附、反应和解吸过程中的使用程度。如果内部构成没有被利用，那么实际上会浪费大量的催化剂材料，我们可能会使用无孔催化剂，就像整体式反应器中一样。对于非常活跃的催化剂，通常不需要多孔颗粒提供的扩大的表面积。

在宏观尺度上详细描述大多数均质颗粒

一旦知道均质颗粒模型为我们提供了详细几何结构的近似值，就可以使用这种近似值来描述固定床反应器中的大量粒子。微反应器模型就是这样一个例子，其详细的几何形状可以使用微建模技术构建。这种反应器可用于详细的动力学研究和芯片上实验室（LOC）设备。

此外，在这种情况下，我们有两种类型的域：一种用于本体流体，另一种用于多孔颗粒。我们还发现，在本体流体和多孔颗粒之间的内部边界上，通量和浓度是连续性的。

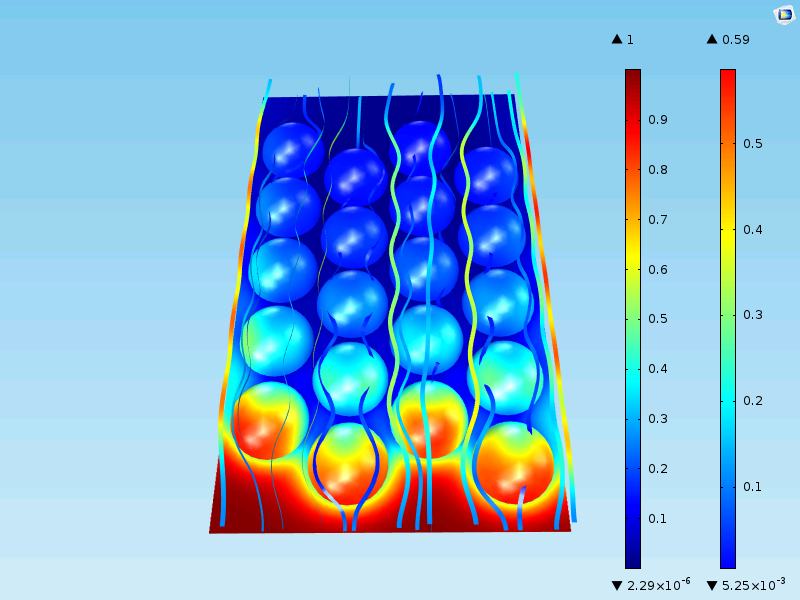
现在，催化剂颗粒外的本体混合物中的浓度也降低到很小的数值。颗粒表面的最大浓度仍然相同，为 0.59mol/m³。这是意料之中的，因为第一排粒子通过的入口与上面的单粒子模型几乎相同。

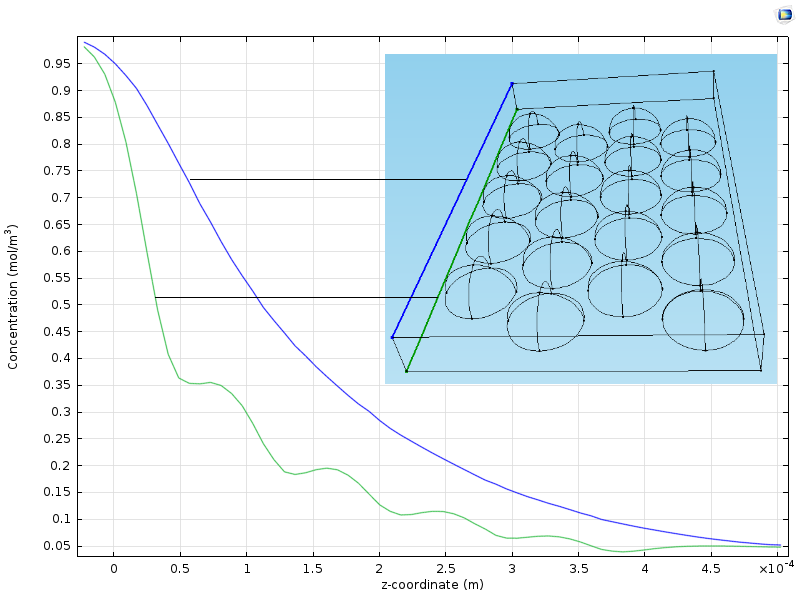
下图显示了沿两条垂直线从入口到出口的浓度的两个图。一条线在略高于颗粒的平面中运行，另一条线沿颗粒中心的位置在平面中运行。可以看到，沿着靠近颗粒的线（绿色）的曲线以波浪图揭示了颗粒的位置。沿着离颗粒稍远的线的浓度曲线是平滑的，因为它通过扩散变得平滑。从入口到出口，沿着反应器的平均浓度介于绿色和蓝色曲线之间。

宏观尺度上的均质化描述

在上面的例子中，我们引入了催化剂颗粒内部的第一次均质化。见下图：

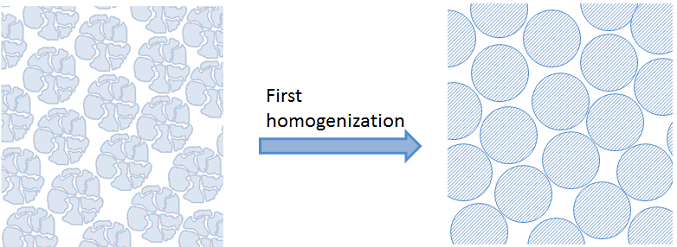
当固定床反应器中的颗粒过多时，与固定床的尺寸相比，这些颗粒也非常小。在这种情况下，我们无法描述床的详细几何形状。相反，我们可以为固定床及其中的本体流体使用第二次均质化。

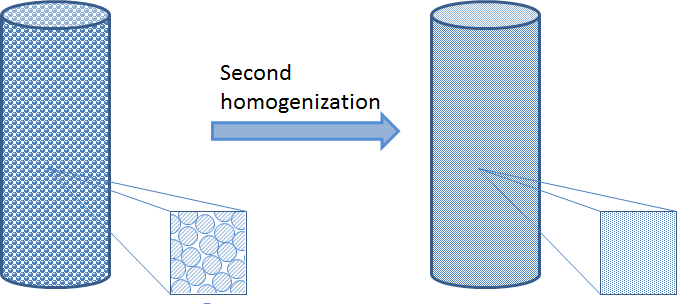
与固定床的尺寸相比，多孔颗粒非常小，我们可以将颗粒折叠到多孔本体域中的源和汇。然而，在这种均质化中，必须保留对围绕每个颗粒的边界层的传递以及多孔颗粒内部的传递-反应过程的描述。我们还必须在多孔本体域中保留传输和流动的近似描述。下图是对非均质化颗粒描述的原理描述。我们可以通过在固定床的每个点上引入一个自变量r来实现这一点，该变量对应于多孔颗粒的半径，包括该粒子外部的边界层。

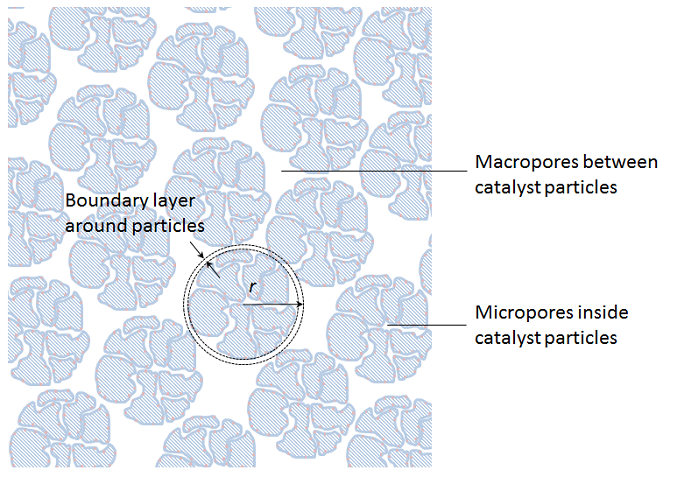
然后，边界层中的传递和颗粒内部的传递反应过程用沿半径的球形对称物质守恒近似。上面示例中详细模型的平流通量主要沿轴向运行（沿颗粒向下的方向），而第二次均质化仅考虑颗粒的径向变化。然而，这种平流中的一些可以解释为略微增加的有效扩散率，在简化描述中，除了分子扩散之外，还描述了分散。

如果我们在三维空间中对固定床进行建模，这实际上意味着获得了四个独立的空间变量：沿颗粒半径的变量x、y、z和r。第五个自变量是时间。此外，我们必须使用所谓的双峰孔隙率描述，它描述了催化剂颗粒内部的微孔隙率和本体混合物流动的颗粒之间空隙的宏观孔隙率（见上图）。

通过引入多孔颗粒的通量作为多孔体域中的源和汇，获得颗粒尺度的一维传递-反应方程与固定床体体积之间的耦合。相反，体域中的局部浓度是颗粒模型中多孔床中每个点的边界层浓度的边界条件。

将具有相对简单的反应动力学的稳态模型描述为一种浓度的多项式，可以用解析法求解沿颗粒半径（包括边界层）的传递反应过程。通过使用Thiele modulus 模量和有效因子列出不同类型的颗粒和动力学反应阶数，将这种解制成表格。在这种情况下，多孔颗粒进出通量的解析表达式被用作固定床中大部分流体的物质守恒中的源和汇。

此外，在宏观尺度上，均质化近似的精度取决于固定床尺寸与颗粒相对尺寸的比较。近似值的精度随着粒径的减小而增加。

我们可能还会注意到一些有趣的事情。如果在固定床反应器中沿宽度和深度（如果是圆柱形反应堆，则为半径）有微小的变化，我们可以用一维模型沿反应堆的高度（从入口到出口）描述宏观模型。我们得到的模型具有两个独立的空间变量，一个在z方向，一个是多孔催化剂颗粒半径r。对于上面的微反应器，这种简化与沿高度的平均浓度和反应物总转化率的更加详细的模型具有很好的一致性。

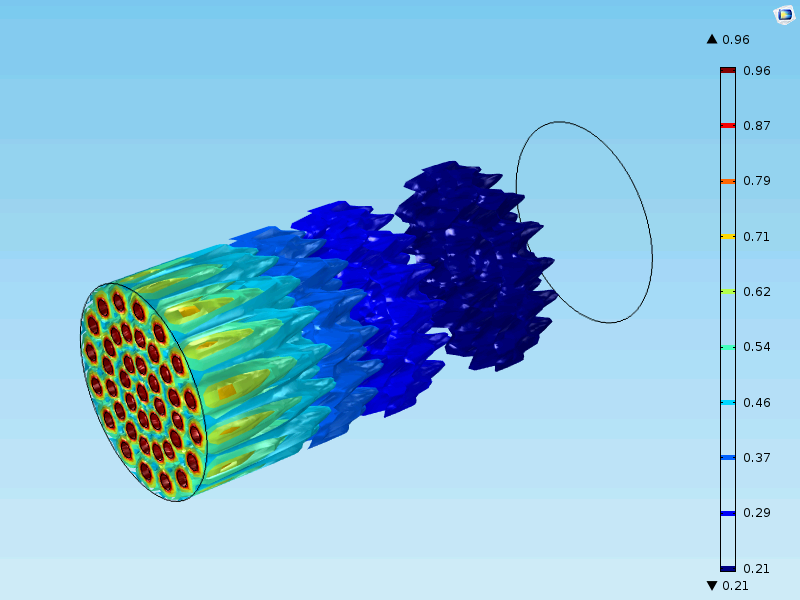
下图显示了与上述建模不同的情况。在这里，反应器的尺度为米级，固定床中有数百万个催化剂颗粒。催化剂的活性比我们截至目前研究的案例要低。图中的固定床反应器不能用一维模型简化，因为入口喷嘴（红色）会影响反应器中的浓度分布。在这种情况下，模型在宏观尺度上是三维的，具有一个额外的第四维颗粒半径，和第五个独立变量时间。

结束语

这篇博客，我们在微观尺度上描述了非常复杂的催化物几何结构，包括传递、吸附、反应和解吸步骤。

这种描述使用均质化的方法在微观水平上近似，将催化剂颗粒描述为多孔板。

接着，使用简化的颗粒模型对大量颗粒进行建模，随后详细描述了每个颗粒的位置和形状，只简化了颗粒的内部结构。

然后，当颗粒数量变得过多时，我们还在宏观反应器尺度上对固定床域进行了均质化处理。

遵循均质化和近似化的过程，从微观颗粒尺度到宏观反应器尺度，我们可以详细设计催化剂并研究该设计对整个反应器性能的影响。此外，这种方法也可以“反向”使用。换句话说，我们可以研究宏观操作如何影响微观尺度的操作条件，从而使我们能够根据反应器中不同位置的相关操作条件调整催化剂和床层设计。