模拟盘管换热器

盘管换热器非常简单，且容易制造。在这篇博客中，我们考察了一个轴向环绕的铜盘管，它通过输运热水来加热圆形管道内的空气。因为沿中心线两侧的几何几乎相同，所以模型使用二维轴对称面求解； 同时增加了额外的表达式来计算盘管匝间的温降，这大大简化了模拟。

盘管换热器模型

下图显示了我们将考察的盘管换热器。

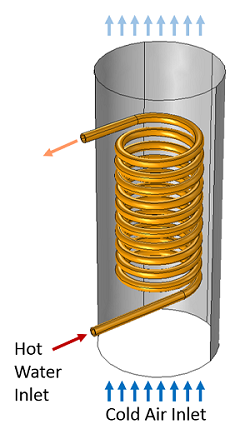
铜盘管在有冷空气流经的管道内输运热水。

铜盘管呈螺旋缠绕，以便沿轴向插入圆形空气管道的内部。冷空气在管道内流动，热水由盘管泵入。使用共轭传热接口计算空气流场，以及空气与铜管的温度。由于几何基本为轴对称，我们可以假定模型与气流完全轴对称，以简化模拟。因此，我们可以使用二维轴对称共轭传热接口。气流速度很高，所以使用了一个湍流模型； 此例中，为 k-epsilon 模型。

我们可以假定管道内流动的水为经充分发展的流动。同时我们也可以假定水温的变化很小，密度不变，所以平均速度保持恒定。因此，我们不需要模拟水的流动，而是可以利用强制对流传热关系式模拟流体和管壁之间的传热。

‘对流热通量’边界条件使用强制内部对流 Nusselt 数关系式来计算水与铜盘管之间的传热， 在铜盘管的所有内部边界上都应用了此边界条件。输入项包括管道几何、流体类型、流体速度，以及流体温度。除了流体温度之外，所有这些量在盘管每匝中保持不变。

模拟盘管匝间的温降

热水被泵入铜盘管后，开始冷却。但由于是轴对称模型，每匝盘管独立于其他盘管匝，除非我们人为设定它们之间的相互关系。这就是说，我们必须在每匝盘管的内边界应用单独的‘对流热通量’边界条件。

这会带来一个问题： 我们如何计算每匝之间的温降，并将它加入我们的模型中？

考虑水流经一匝铜盘管时的情景。水的热损失等于向铜管传递的热量。假定材料属性恒定，且忽略粘性损耗，那么水在流经一匝管道之后的温降为：

其中，\dot m是质量流率、C_p是水的等压热容、Q是水的总热损失，它等于铜中的热通量沿盘管内部边界上的积分。这一积分可以通过定义在盘管内部边界上的积分组件耦合计算。

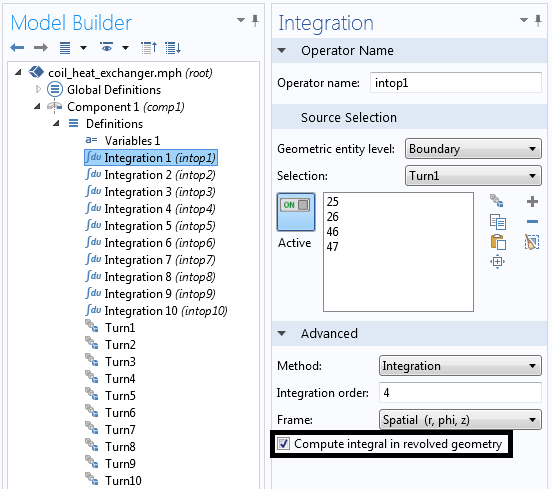
边界上定义的积分组件耦合。注意： 该积分在旋转几何中计算。

使用这些耦合算子，我们可以针对温降定义一组用户定义变量：

DT1 = intop1(-nitf.nteflux/mdot0/Cp0)

这计算了沿盘管第一匝的温降。我们可以为管道的每一匝定义不同的温降变量，并依次在每匝中使用。

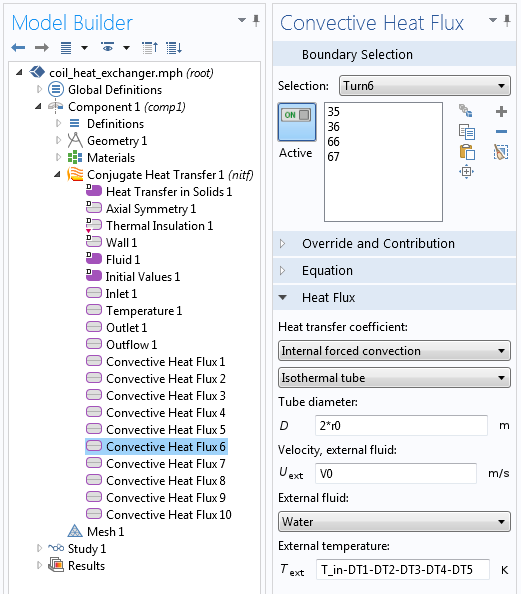
第六匝的水温考虑到了前五匝的温降。

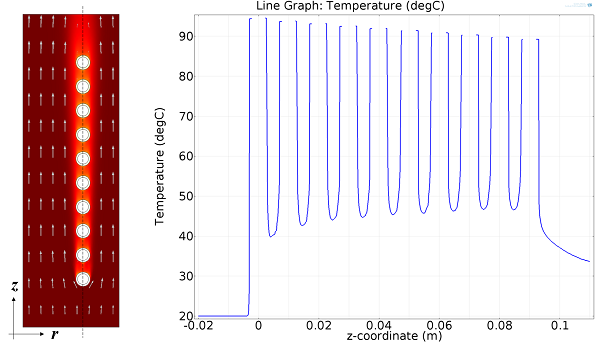
流场与温度绘图（左）；沿盘管中心线的温度（右）。

由于这是一个二维轴对称模型，所以求解非常快。我们可以检查温度和流场，并沿盘管中心线绘制温降。我们可以观察到水在盘管每匝之间逐渐降温，空气则被加热。

这可以看作一个平行流换热器，因为热流体流动与冷流体流动的总方向相同。如果我们希望将该模型改为反向流动配置，则可以通过交换空气的入口与出口条件轻松实现，这样流体就会沿相反的方向流动。

您觉得这一技巧还可以模拟哪些换热器配置呢？